华师大版数学八上13.2.6三角形全等的判定斜边直角边课件(共25张PPT)
文档属性
| 名称 | 华师大版数学八上13.2.6三角形全等的判定斜边直角边课件(共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 805.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-31 13:30:15 | ||
图片预览




文档简介
(共25张PPT)
华东师大版·八年级上册
13.2.6斜边直角边
新课导入
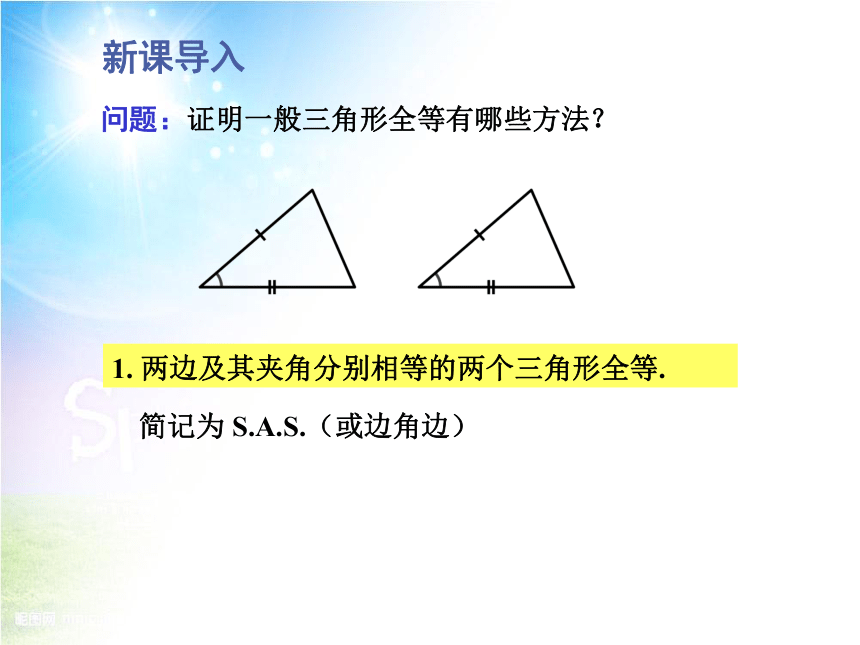
问题:证明一般三角形全等有哪些方法?
1. 两边及其夹角分别相等的两个三角形全等.
简记为 S.A.S.(或边角边)
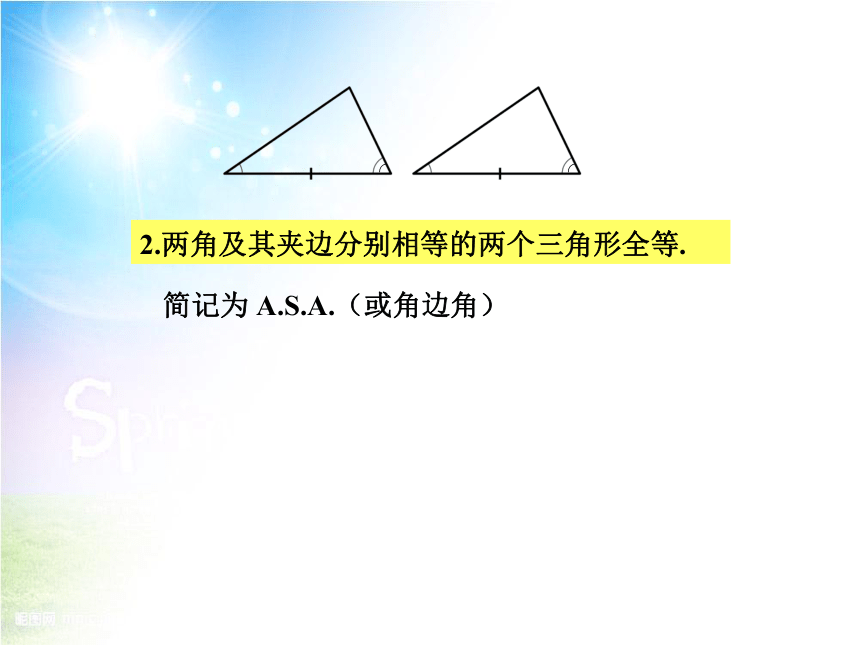
2.两角及其夹边分别相等的两个三角形全等.
简记为 A.S.A.(或角边角)
3.两角分别相等且其中一组等角的对边相等的
两个三角形全等.
简记为 A.A.S.(或角角边).
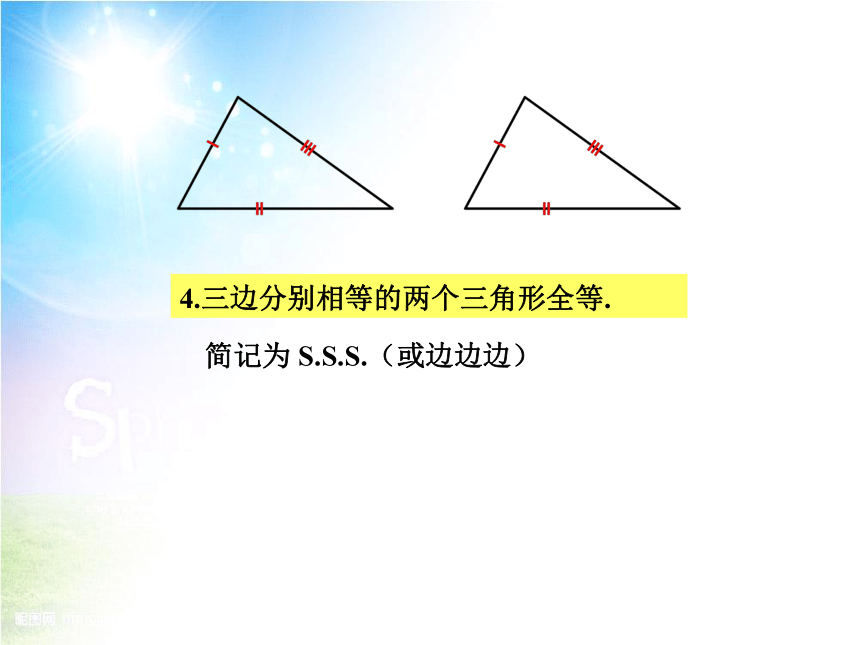
4.三边分别相等的两个三角形全等.
简记为 S.S.S.(或边边边)
探究新知
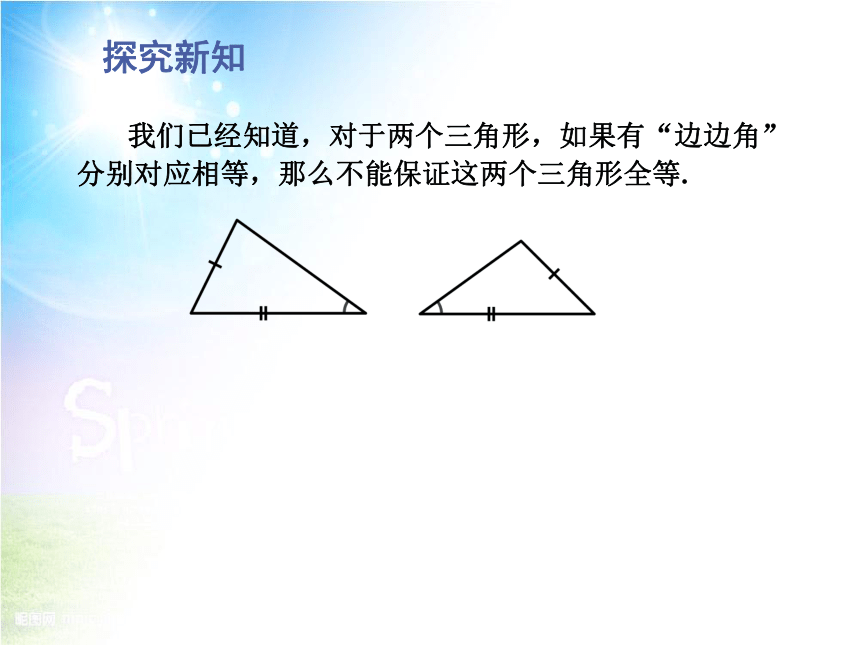
我们已经知道,对于两个三角形,如果有“边边角”分别对应相等,那么不能保证这两个三角形全等.
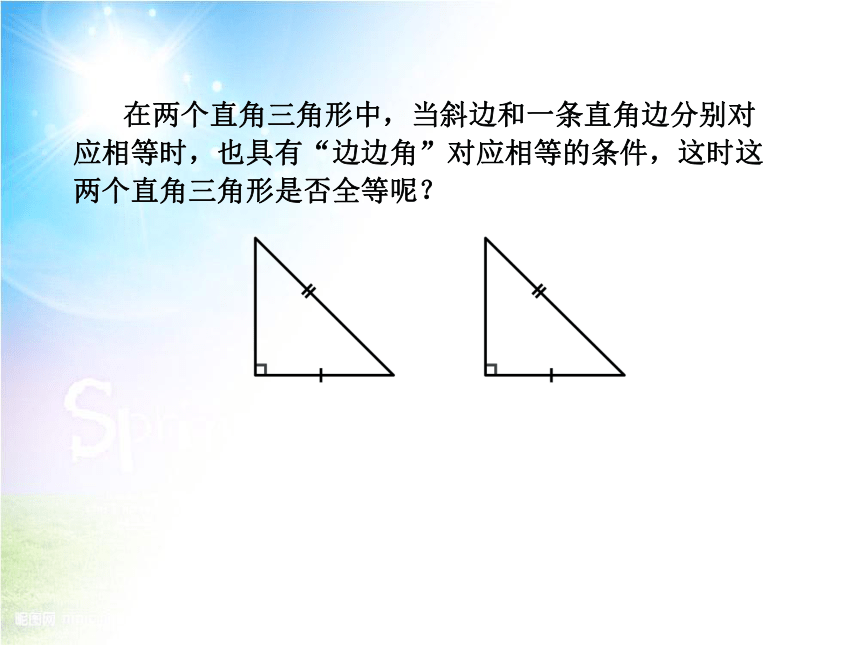
在两个直角三角形中,当斜边和一条直角边分别对应相等时,也具有“边边角”对应相等的条件,这时这两个直角三角形是否全等呢?
做
一
做
如图,已知两条线段(这两条线段长不相等),试画一个直角三角形,使长的线段为其斜边、短的线段为其一条直角边.
步骤:
1.画一条线段AB,使它等于 2 cm;
2.画∠MAB = 90°(用量角器或三角尺);
3.以点 B 为圆心、3 cm 长为半径画圆弧,交射线 AM于点C;
4.连结 BC.
△ABC 即为所求.
把你画的直角三角形与其他同学画的直角三角形进行比较,或将你画的直角三角形剪下,放到其他同学画的直角三角形上,看看是否完全重合. 所画的直角三角形都全等吗?
换两条线段,试试看,是否有同样的结论?
斜边和一条直角边分别相等的两个直角三角形全等.
简记为 H.L.(或斜边直角边).
例
如图,已知 AC = BD,∠C = ∠D = 90°.求证: BC = AD.
证明: ∵∠C = ∠D = 90°(已知),
∴△ABC与△BAD 都是直角三角形(直角三角形的定义).
在Rt△ABC 与 Rt△BAD 中,
∵AB = BA (公共边),
AC = BD (已知),
∴Rt△ABC ≌ Rt△BAD (H.L.)
BC = AD (全等三角形的对应边相等).
1. 一般三角形的全等与直角三角形的全等是从一般到特殊的关系,二者之间的联系为: 一般三角形的判定方法同样适用于直角三角形.
2.判定一般三角形的全等与直角三角形的全等的区别:
(1)一般三角形全等的条件“S.S.S.”在直角三角形中被“H.L.”代替,无需找第三条边对应相等;
(2)“两边及其中一边的对角对应相等”不能判定一般三角形全等,但能判定直角三角形全等.
练 习
如图,在△ABC中,D为 BC 的中点,DE⊥AB,DF⊥AC,点 E、F 为垂足,DE = DF. 求证:△BED≌△CFD.
证明: ∵ DE ⊥ AB,DF ⊥ AC,
∴ ∠BED = ∠CFD = 90°,
∴△BED 与△CFD 都是直角三角形.
∵D 为 BC 的中点,
∴BD = CD .
在 Rt△BED 与 Rt△CFD 中,
∵BD = CD ,DE = DF,
∴Rt△BED ≌ Rt△CFD (H.L.).
2. 如图,AC = AD,∠C =∠D = 90°.求证: BC = BD.
证明:在Rt△ACB 和Rt△ADB 中,
∵AB=AB,AC=AD ,
∴Rt△ACB≌ Rt△ADB (H.L.).
∴BC = BD .
如图,有两个长度相同的滑梯,左边滑梯的高度 AC 与右边滑梯水平方向的跨度 DF 相等,两个滑梯的倾斜角∠B 与 ∠F 的大小有什么关系?说说你的想法和理由.
解: ∠B+∠F = 90°.
可以利用已知条件证明
Rt△ABC ≌ Rt△DEF (H.L.),
∴∠B =∠DEF,
∴∠B+∠F = 90°.
习题13.2
1.如图,已知 AB = DC, AC = DB. 求证:△ABC≌△DCB.
证明:在△ABC 和△DCB 中,
∵AB=DC,AC=DB,BC=CB,
∴△ABC≌△DCB (S.S.S.).
2. 如图,已知∠1 = ∠2,AO = BO . 求证: △AOP≌△BOP.
证明: 在△AOP 和△BOP 中,
∵OP = OP ,∠1=∠2,OA =OB,
∴△AOP ≌ △BOP (S.A.S.).
3.如图,要使各对三角形全等,还需要增加什么条件?
(1)∠A =∠D,∠B = ∠F ;
(2)∠A =∠D,AB = DE.
(1)
(2)
解: (1)AB=DF (或AC=DE 或 BC=FE);
(2)∠B=∠E (或∠C=∠F 或 AC=DF).
4. 如图,已知 AB 与 CD 相交于点 O,∠A = ∠D,
CO = BO. 求证:△AOC≌△DOB.
证明: 在△AOC 和△DOB 中,
∵∠A =∠D ,∠AOC=∠DOB,
CO=BO,
∴△AOC≌△DOB (A.A.S.)
5. 如图,∠1 = ∠2,∠3 =∠4 . 求证: AB = AC.
证明: ∵∠3=∠4,
∴∠ADC=∠ADB.
在△ADC 和△ADB 中,
∵∠1=∠2,AD =AD,∠ADC=∠ADB,
∴△ADC≌△ADB (A.S.A.),
∴AB = AC.
6. 如图,在△ABC中,AB = AC,AD是边 BC 上的高.
求证:(1)BD = DC;(2)∠BAD = ∠CAD.
证明: ∵AD 是 BC 边上的高,
∴∠ADB =∠ADC=90°.
在Rt△ADB 和Rt△ADC 中,
AB=AC,AD = AD,
∴Rt△ADB ≌ Rt△ADC (H.L.),
∴BD = DC,∠BAD =∠CAD .
一名工作人员不慎将一块三角形模具打碎成两块,他是否可以只带其中一块碎片到商店去,就能配一块与原来一样的三角形模具呢?他该带哪块去呢?请用数学知识解释你的结论.
解:可以.带右边的一块去.这样可以根据三角形全等的判定方法可知,具有全等的 3 个条件,即 A.S.A.
课堂小结
斜边直角边
判定定理
形式
斜边和一条直角边分别相等的两个直角三角形全等
H.L.(斜边直角边),存在于直角三角形中
判定直角三角形全等与判定一般三角形全等的联系与区别
应用
用H.L.解决问题
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
华东师大版·八年级上册
13.2.6斜边直角边
新课导入
问题:证明一般三角形全等有哪些方法?
1. 两边及其夹角分别相等的两个三角形全等.
简记为 S.A.S.(或边角边)
2.两角及其夹边分别相等的两个三角形全等.
简记为 A.S.A.(或角边角)
3.两角分别相等且其中一组等角的对边相等的
两个三角形全等.
简记为 A.A.S.(或角角边).
4.三边分别相等的两个三角形全等.
简记为 S.S.S.(或边边边)
探究新知
我们已经知道,对于两个三角形,如果有“边边角”分别对应相等,那么不能保证这两个三角形全等.
在两个直角三角形中,当斜边和一条直角边分别对应相等时,也具有“边边角”对应相等的条件,这时这两个直角三角形是否全等呢?
做
一
做
如图,已知两条线段(这两条线段长不相等),试画一个直角三角形,使长的线段为其斜边、短的线段为其一条直角边.
步骤:
1.画一条线段AB,使它等于 2 cm;
2.画∠MAB = 90°(用量角器或三角尺);
3.以点 B 为圆心、3 cm 长为半径画圆弧,交射线 AM于点C;
4.连结 BC.
△ABC 即为所求.
把你画的直角三角形与其他同学画的直角三角形进行比较,或将你画的直角三角形剪下,放到其他同学画的直角三角形上,看看是否完全重合. 所画的直角三角形都全等吗?
换两条线段,试试看,是否有同样的结论?
斜边和一条直角边分别相等的两个直角三角形全等.
简记为 H.L.(或斜边直角边).
例
如图,已知 AC = BD,∠C = ∠D = 90°.求证: BC = AD.
证明: ∵∠C = ∠D = 90°(已知),
∴△ABC与△BAD 都是直角三角形(直角三角形的定义).
在Rt△ABC 与 Rt△BAD 中,
∵AB = BA (公共边),
AC = BD (已知),
∴Rt△ABC ≌ Rt△BAD (H.L.)
BC = AD (全等三角形的对应边相等).
1. 一般三角形的全等与直角三角形的全等是从一般到特殊的关系,二者之间的联系为: 一般三角形的判定方法同样适用于直角三角形.
2.判定一般三角形的全等与直角三角形的全等的区别:
(1)一般三角形全等的条件“S.S.S.”在直角三角形中被“H.L.”代替,无需找第三条边对应相等;
(2)“两边及其中一边的对角对应相等”不能判定一般三角形全等,但能判定直角三角形全等.
练 习
如图,在△ABC中,D为 BC 的中点,DE⊥AB,DF⊥AC,点 E、F 为垂足,DE = DF. 求证:△BED≌△CFD.
证明: ∵ DE ⊥ AB,DF ⊥ AC,
∴ ∠BED = ∠CFD = 90°,
∴△BED 与△CFD 都是直角三角形.
∵D 为 BC 的中点,
∴BD = CD .
在 Rt△BED 与 Rt△CFD 中,
∵BD = CD ,DE = DF,
∴Rt△BED ≌ Rt△CFD (H.L.).
2. 如图,AC = AD,∠C =∠D = 90°.求证: BC = BD.
证明:在Rt△ACB 和Rt△ADB 中,
∵AB=AB,AC=AD ,
∴Rt△ACB≌ Rt△ADB (H.L.).
∴BC = BD .
如图,有两个长度相同的滑梯,左边滑梯的高度 AC 与右边滑梯水平方向的跨度 DF 相等,两个滑梯的倾斜角∠B 与 ∠F 的大小有什么关系?说说你的想法和理由.
解: ∠B+∠F = 90°.
可以利用已知条件证明
Rt△ABC ≌ Rt△DEF (H.L.),
∴∠B =∠DEF,
∴∠B+∠F = 90°.
习题13.2
1.如图,已知 AB = DC, AC = DB. 求证:△ABC≌△DCB.
证明:在△ABC 和△DCB 中,
∵AB=DC,AC=DB,BC=CB,
∴△ABC≌△DCB (S.S.S.).
2. 如图,已知∠1 = ∠2,AO = BO . 求证: △AOP≌△BOP.
证明: 在△AOP 和△BOP 中,
∵OP = OP ,∠1=∠2,OA =OB,
∴△AOP ≌ △BOP (S.A.S.).
3.如图,要使各对三角形全等,还需要增加什么条件?
(1)∠A =∠D,∠B = ∠F ;
(2)∠A =∠D,AB = DE.
(1)
(2)
解: (1)AB=DF (或AC=DE 或 BC=FE);
(2)∠B=∠E (或∠C=∠F 或 AC=DF).
4. 如图,已知 AB 与 CD 相交于点 O,∠A = ∠D,
CO = BO. 求证:△AOC≌△DOB.
证明: 在△AOC 和△DOB 中,
∵∠A =∠D ,∠AOC=∠DOB,
CO=BO,
∴△AOC≌△DOB (A.A.S.)
5. 如图,∠1 = ∠2,∠3 =∠4 . 求证: AB = AC.
证明: ∵∠3=∠4,
∴∠ADC=∠ADB.
在△ADC 和△ADB 中,
∵∠1=∠2,AD =AD,∠ADC=∠ADB,
∴△ADC≌△ADB (A.S.A.),
∴AB = AC.
6. 如图,在△ABC中,AB = AC,AD是边 BC 上的高.
求证:(1)BD = DC;(2)∠BAD = ∠CAD.
证明: ∵AD 是 BC 边上的高,
∴∠ADB =∠ADC=90°.
在Rt△ADB 和Rt△ADC 中,
AB=AC,AD = AD,
∴Rt△ADB ≌ Rt△ADC (H.L.),
∴BD = DC,∠BAD =∠CAD .
一名工作人员不慎将一块三角形模具打碎成两块,他是否可以只带其中一块碎片到商店去,就能配一块与原来一样的三角形模具呢?他该带哪块去呢?请用数学知识解释你的结论.
解:可以.带右边的一块去.这样可以根据三角形全等的判定方法可知,具有全等的 3 个条件,即 A.S.A.
课堂小结
斜边直角边
判定定理
形式
斜边和一条直角边分别相等的两个直角三角形全等
H.L.(斜边直角边),存在于直角三角形中
判定直角三角形全等与判定一般三角形全等的联系与区别
应用
用H.L.解决问题
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
