2021-2022学年数学人教A版(2019)必修第一册2.3二次函数与一元二次方程、不等式题型归纳练习卷(Word含答案)
文档属性
| 名称 | 2021-2022学年数学人教A版(2019)必修第一册2.3二次函数与一元二次方程、不等式题型归纳练习卷(Word含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 525.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-30 00:00:00 | ||
图片预览



文档简介
二次函数与一元二次方程、不等式
解一元二次不等式(包括分式型不等式、绝对值不等式)
一般步骤:① 求根;② 作图;③ 大于取上,小于取下.
注意:高次分式不等式可用“穿针引线法”.
例:
(1)解下列不等式∶
① ②
(2)求下列不等式的解集:
① ; ② .
(3)不等式<0的解集为( )
A.[0,2] B.(0,2] C.(-∞,0)∪[2,+∞) D.(0,2)
(4)不等式成立的一个必要不充分条件是( )
A. B. C. D.
(5)不等式的解集为___________.
(6)解关于的不等式
已知二次不等式解集求参数值
注意:解集的端点值即为方程的根,偶尔会有韦达定理的考察.
例:
(7)已知,,关于x的不等式的解集为求m,n的值;
(8)已知函数.若不等式的解集为,求a,b的值;
(9)若不等式的解集为,则不等式的解集为( )
A.或 B.
C. D.或
(10)已知,则关于的不等式的解集为( )
A. B.
C.或 D.或
(11)已知不等式解集为,下列结论正确的是( )
A. B.
C. D.
(12)(多选题)若不等式的解集是,则以下正确的有( )
A.a<0 B. C. D.的解集为(﹣2,)
(13)设m n是方程的两个实数根,则的值为___________.
(14)已知a<0且关于x的不等式x2-4ax+3a2<0解集为{x|x1A.- B.- C. D.
二次不等式恒成立或无解,求参数值或范围
注意:
① 定义域为R,限制条件为:开口方向、;
② 定义域不是R,限制条件为:开口()、端点值正负、对称轴位置;
③ 恒成立问题两种解题思路:直接分析、分离参数;
④ 二次项系数为参数的,要考虑是否需要分类讨论.
例:
(15)若不等式的解集为空集,则的取值范围是( )
A. B.,或
C. D.,或
(16)若关于的不等式在上恒成立,则实数的取值范围是______.
(17)关于不等式恒成立,则实数的取值范围是___________.
(18)命题“”为真命题的一个充分不必要条件是( )
A. B. C. D.
(19)关于x的不等式x2+ax+a≤1对一切x∈(0,1)恒成立,则a的取值范围为___________.
(20)已知二次函数.若时,不等式恒成立,求实数的取值范围.
(21)命题,使得成立.若是假命题,则实数的取值范围是( )
A. B.
C. D.
(22)对任意实数,不等式恒成立,则实数的取值范围是( )
A. B. C. D.
二次不等式存在性问题
注意:正难则反,情况复杂时转化成恒成立问题,求相反的情况.
例:
(23)若存在x使得有正值,则m的取值范围是( )
A.或 B. C. D.
(24)已知二次函数.
① 若存在使成立,求的取值范围;
② 当时,求在区间上的最小值.
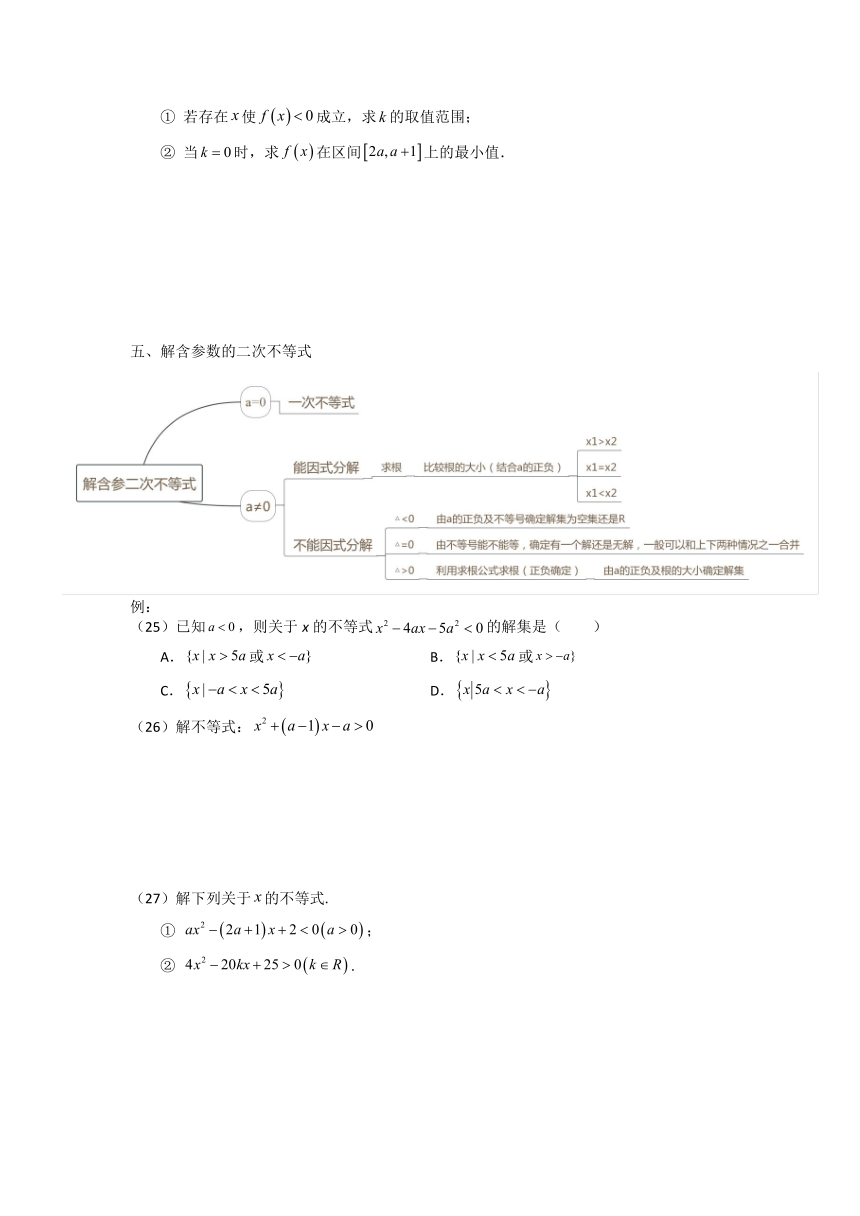
解含参数的二次不等式
例:
(25)已知,则关于x的不等式的解集是( )
A.或 B.或
C. D.
(26)解不等式:
(27)解下列关于的不等式.
① ;
② .
实际应用
例:
一名同学以初速度竖直上抛一排球,排球能够在抛出点以上的位置最多停留多长时间?(竖直上抛的物体距离抛出点的高度与时间满足关系:,其中)
市场上有这样一个规律,商品价格愈高,购买的人愈少;价格越近,购买的人就多,一淘宝店主若以每件2元的价格销售某商品,则年销售量为10万件,若他把每件商品的定价每提高0.2元,销售量就相应减少5000件,如果淘宝店主希望该商品的年销售额不少于22.4万元,试求该商品的合理销售价格范围.
(30)十九大以来,国家深入推进精准脱贫,加大资金投入,强化社会帮扶,为了更好的服务于人民,派调查组到某农村去考察和指导工作.该地区有200户农民,且都从事水果种植,据了解,平均每户的年收入为3万元.为了调整产业结构,调查组和当地政府决定动员部分农民从事水果加工,据估计,若能动员户农民从事水果加工,则剩下的继续从事水果种植的农民平均每户的年收入有望提高,而从事水果加工的农民平均每户收入将为万元.
① 若动员户农民从事水果加工后,要使从事水果种植的农民的总年收入不低于动员前从事水果种植的农民的总年收入,求的取值范围;
② 在①的条件下,要使这200户农民中从事水果加工的农民的总收入始终不高于从事水果种植的农民的总收入,求的最大值.
参考答案
① ;② 或
①或;② 或
D
D
或
,
D
D
C
ABC
1000
A
A
B
A
C
A
① ;②
D
(26)原不等式可化为
当时,解集为
当时,解集为
当时,解集为
(27)①
当,即时,不等式的解集为;
当,即时,不等式的解集为;
当,即时,不等式的解集为.
② 由题意知:,
当时,,不等式的解集为;
当时,,不等式的解集为;
当或时,令,解得:,
不等式的解集为;
当时,,不等式的解集为
(28)
(29)
(30)① ;②
解一元二次不等式(包括分式型不等式、绝对值不等式)
一般步骤:① 求根;② 作图;③ 大于取上,小于取下.
注意:高次分式不等式可用“穿针引线法”.
例:
(1)解下列不等式∶
① ②
(2)求下列不等式的解集:
① ; ② .
(3)不等式<0的解集为( )
A.[0,2] B.(0,2] C.(-∞,0)∪[2,+∞) D.(0,2)
(4)不等式成立的一个必要不充分条件是( )
A. B. C. D.
(5)不等式的解集为___________.
(6)解关于的不等式
已知二次不等式解集求参数值
注意:解集的端点值即为方程的根,偶尔会有韦达定理的考察.
例:
(7)已知,,关于x的不等式的解集为求m,n的值;
(8)已知函数.若不等式的解集为,求a,b的值;
(9)若不等式的解集为,则不等式的解集为( )
A.或 B.
C. D.或
(10)已知,则关于的不等式的解集为( )
A. B.
C.或 D.或
(11)已知不等式解集为,下列结论正确的是( )
A. B.
C. D.
(12)(多选题)若不等式的解集是,则以下正确的有( )
A.a<0 B. C. D.的解集为(﹣2,)
(13)设m n是方程的两个实数根,则的值为___________.
(14)已知a<0且关于x的不等式x2-4ax+3a2<0解集为{x|x1
二次不等式恒成立或无解,求参数值或范围
注意:
① 定义域为R,限制条件为:开口方向、;
② 定义域不是R,限制条件为:开口()、端点值正负、对称轴位置;
③ 恒成立问题两种解题思路:直接分析、分离参数;
④ 二次项系数为参数的,要考虑是否需要分类讨论.
例:
(15)若不等式的解集为空集,则的取值范围是( )
A. B.,或
C. D.,或
(16)若关于的不等式在上恒成立,则实数的取值范围是______.
(17)关于不等式恒成立,则实数的取值范围是___________.
(18)命题“”为真命题的一个充分不必要条件是( )
A. B. C. D.
(19)关于x的不等式x2+ax+a≤1对一切x∈(0,1)恒成立,则a的取值范围为___________.
(20)已知二次函数.若时,不等式恒成立,求实数的取值范围.
(21)命题,使得成立.若是假命题,则实数的取值范围是( )
A. B.
C. D.
(22)对任意实数,不等式恒成立,则实数的取值范围是( )
A. B. C. D.
二次不等式存在性问题
注意:正难则反,情况复杂时转化成恒成立问题,求相反的情况.
例:
(23)若存在x使得有正值,则m的取值范围是( )
A.或 B. C. D.
(24)已知二次函数.
① 若存在使成立,求的取值范围;
② 当时,求在区间上的最小值.
解含参数的二次不等式
例:
(25)已知,则关于x的不等式的解集是( )
A.或 B.或
C. D.
(26)解不等式:
(27)解下列关于的不等式.
① ;
② .
实际应用
例:
一名同学以初速度竖直上抛一排球,排球能够在抛出点以上的位置最多停留多长时间?(竖直上抛的物体距离抛出点的高度与时间满足关系:,其中)
市场上有这样一个规律,商品价格愈高,购买的人愈少;价格越近,购买的人就多,一淘宝店主若以每件2元的价格销售某商品,则年销售量为10万件,若他把每件商品的定价每提高0.2元,销售量就相应减少5000件,如果淘宝店主希望该商品的年销售额不少于22.4万元,试求该商品的合理销售价格范围.
(30)十九大以来,国家深入推进精准脱贫,加大资金投入,强化社会帮扶,为了更好的服务于人民,派调查组到某农村去考察和指导工作.该地区有200户农民,且都从事水果种植,据了解,平均每户的年收入为3万元.为了调整产业结构,调查组和当地政府决定动员部分农民从事水果加工,据估计,若能动员户农民从事水果加工,则剩下的继续从事水果种植的农民平均每户的年收入有望提高,而从事水果加工的农民平均每户收入将为万元.
① 若动员户农民从事水果加工后,要使从事水果种植的农民的总年收入不低于动员前从事水果种植的农民的总年收入,求的取值范围;
② 在①的条件下,要使这200户农民中从事水果加工的农民的总收入始终不高于从事水果种植的农民的总收入,求的最大值.
参考答案
① ;② 或
①或;② 或
D
D
或
,
D
D
C
ABC
1000
A
A
B
A
C
A
① ;②
D
(26)原不等式可化为
当时,解集为
当时,解集为
当时,解集为
(27)①
当,即时,不等式的解集为;
当,即时,不等式的解集为;
当,即时,不等式的解集为.
② 由题意知:,
当时,,不等式的解集为;
当时,,不等式的解集为;
当或时,令,解得:,
不等式的解集为;
当时,,不等式的解集为
(28)
(29)
(30)① ;②
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
