华师大版数学八上13.2.3全等三角形的判定边角边课件(共23张ppt)
文档属性
| 名称 | 华师大版数学八上13.2.3全等三角形的判定边角边课件(共23张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-31 13:51:18 | ||
图片预览



文档简介
(共23张PPT)
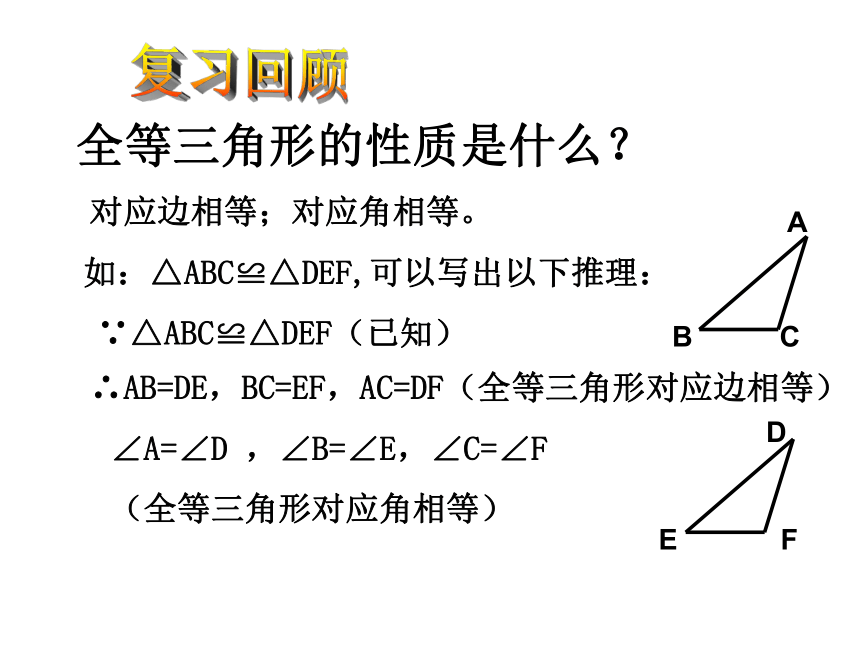
全等三角形的性质是什么?
对应边相等;对应角相等。
如:△ABC≌△DEF,可以写出以下推理:
∵△ABC≌△DEF(已知)
∴AB=DE,BC=EF,AC=DF(全等三角形对应边相等)
∠A=∠D ,∠B=∠E,∠C=∠F
(全等三角形对应角相等)
A
B
C
D
E
F
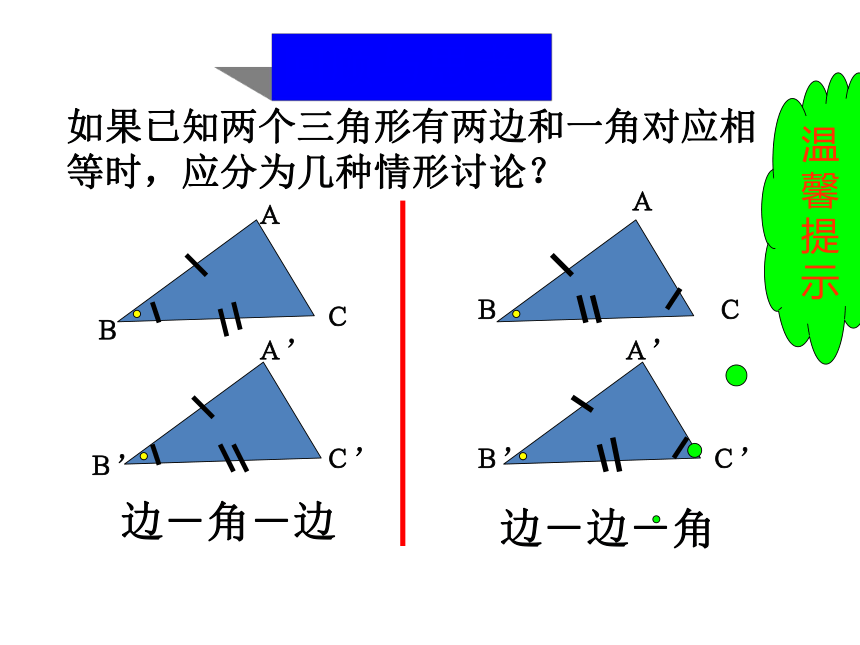
回顾与思考
如果已知两个三角形有两边和一角对应相等时,应分为几种情形讨论?
边-角-边
边-边-角
A
A
A’
A’
B
B’
B
B’
C
C
C’
C’
温馨提示
做一做:画△ABC,使AB=3cm,AC=4cm.
画法:
1. 画线段AB= 3cm;
3. 在射线AM上截取AC=4cm;
这样画出来的三角形与同桌所画的三角形进行比较,它们互相重合吗?
若再加一个条件,使∠A=45°,画出△ABC.
2. 画∠MAB= 45°;
4. 连接BC.
△ABC就是所求的三角形.
把你们所画的三角形剪下来与同桌所画的三角形进行比较,它们能互相重合吗?
探究
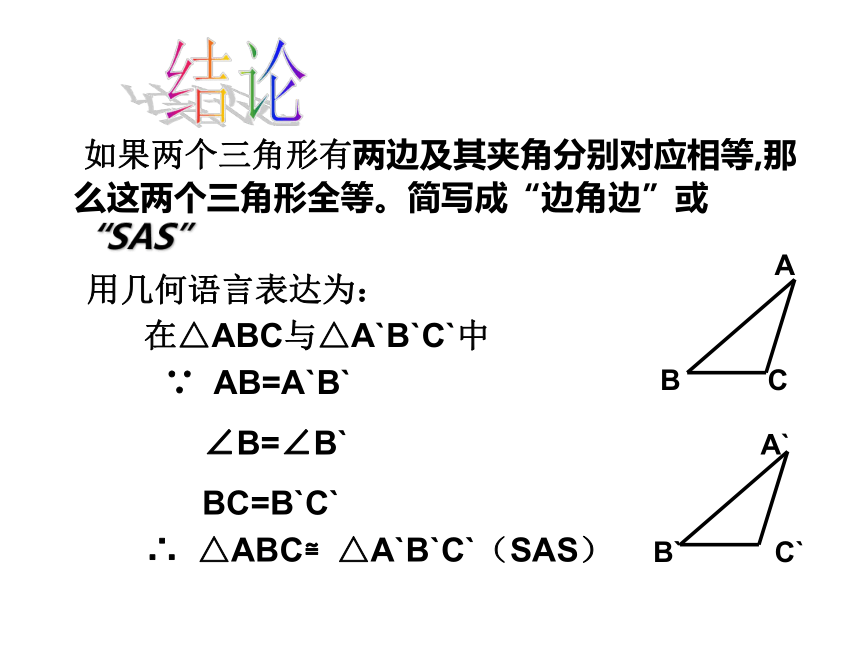
用几何语言表达为:
在△ABC与△A`B`C`中
∴ △ABC≌△A`B`C`(SAS)
如果两个三角形有两边及其夹角分别对应相等,那么这两个三角形全等。简写成“边角边”或“SAS”
∵ AB=A`B`
∠B=∠B`
BC=B`C`
A
B
C
A`
B`
C`
如图△ABC和△ DEF 中,AB=DE=3 ㎝,∠ B=∠ E=300 , BC=EF=5 ㎝,它们完全重合吗?△ABC≌△ DEF吗 ?为什么
3㎝
5㎝
300
A
B
C
3㎝
5㎝
300
D
E
F
它们完全重合,即△ABC≌△ DEF .根据边角边.
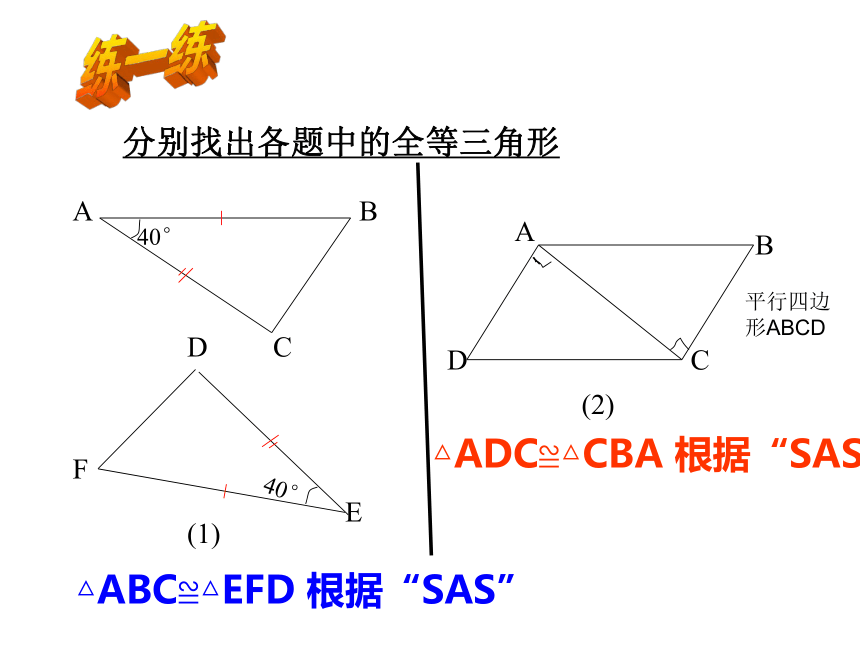
分别找出各题中的全等三角形
A
B
C
40°
40°
D
E
F
(1)
D
C
A
B
(2)
△ABC≌△EFD 根据“SAS”
△ADC≌△CBA 根据“SAS”
平行四边形ABCD
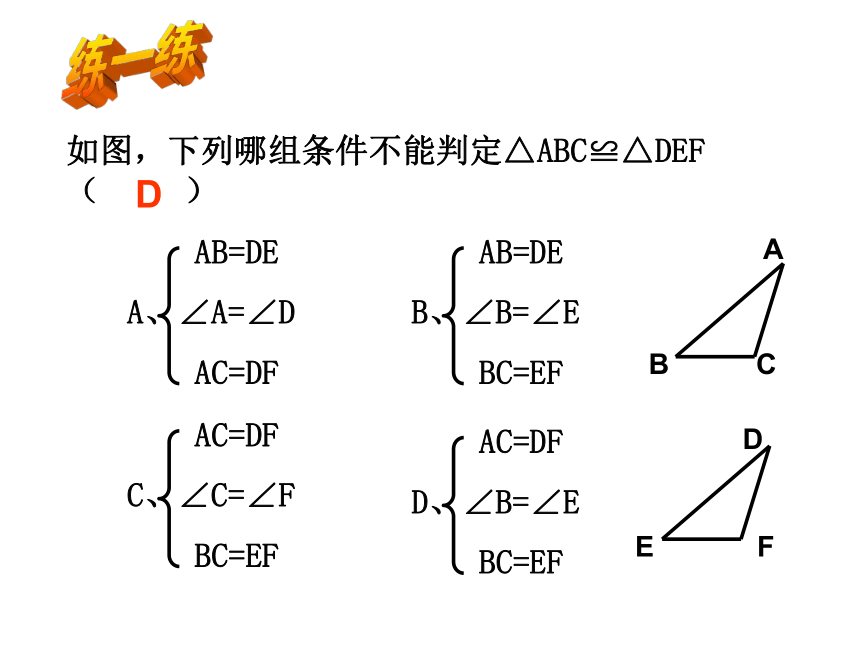
如图,下列哪组条件不能判定△ABC≌△DEF( )
A
B
C
D
E
F
AB=DE
A、∠A=∠D
AC=DF
AC=DF
C、∠C=∠F
BC=EF
AB=DE
B、∠B=∠E
BC=EF
AC=DF
D、∠B=∠E
BC=EF
D
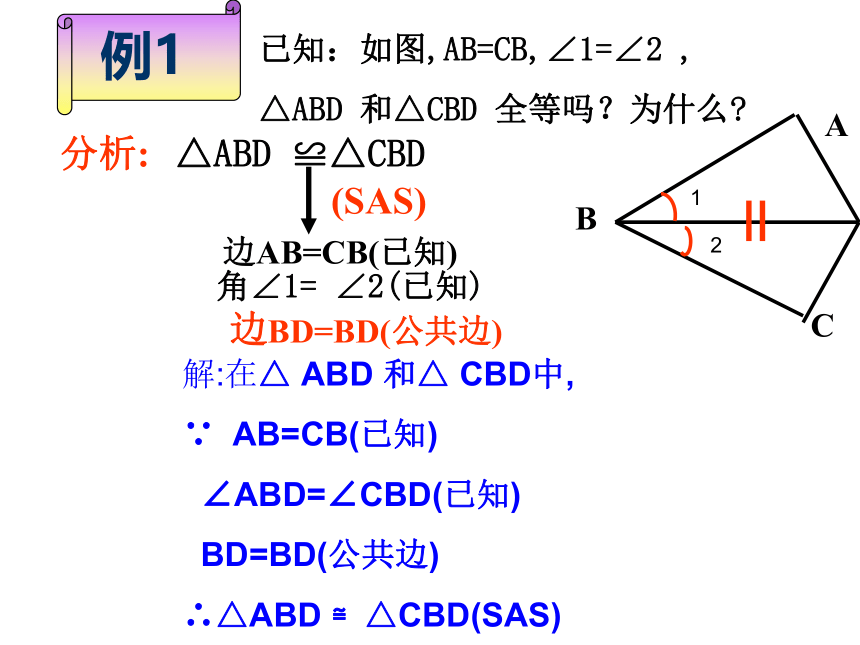
已知:如图,AB=CB,∠1=∠2 ,
△ABD 和△CBD 全等吗?为什么
例1
分析:
△ABD ≌△CBD
边AB=CB(已知)
角∠1= ∠2(已知)
边BD=BD(公共边)
A
B
C
D
(SAS)
解:在△ ABD 和△ CBD中,
∵ AB=CB(已知)
∠ABD=∠CBD(已知)
BD=BD(公共边)
∴△ABD ≌△CBD(SAS)
1
2
已知:如图,AD∥BC,AD=CB.
求证: △ADC≌△CBA
A
B
C
D
1
2
证明:∵AD∥BC
∴ ∠1=∠2(两直线平行,
内错角相等)
在△ADC和△CBA中
∵AD=CB(已知)
∠1=∠2(已证)
AC=CA(公共边)
∴ △ADC≌△CBA(SAS)
已知:如图,AD∥BC,AD=BC,AE=CF.
求证: △AFD≌△CEB
A
D
E
F
B
C
∵AD∥BC
∴ ∠A=∠C(两直线平行,内错角相等)
证明:∵AE=CF
∴AE+EF=CF+EF即AF=CE
在△ADF和△CEB中
∵ AD=CB(已知)
∠A=∠C(已证)
AF=CE(已证)
∴ △AFD≌△CEB(SAS)
已知:如图,AB=AC,AD=AE.
求证: △ABE≌△ACD
A
C
D
B
E
A
证明:在△ABE和△ACD中
∵ AB=AC(已知)
∠A=∠A(公共角)
AD=AE(已知)
∴ △ABE≌△ACD(SAS)
已知:如图,AB=AC,AD=AE, ∠1=∠2.
求证:△ADB≌△ACE
1
A
C
E
2
A
B
D
证明:∵∠1=∠2(已知)
∴ ∠1+∠BAE=∠2+∠BAE,
即∠CAE=∠BAD
在△ADB和△ACE中
∵ AB=AC(已知)
∠CAE=∠BAD(已证)
AD=AE(已知)
∴ △ADB≌△ACE(SAS)
A
B
C
D
O
如图AC与BD相交于点O,已知OA=OC,OB=OD,说明△AOB≌△COD的理由。
解:在△AOB和△COD中
∵ OA=OC(已知)
∠AOB=∠COD(对顶角)
OB=OD(已知)
∴ △AOB≌△COD(SAS)
1.准备条件:证全等时要用的条件 要先证好;
2.三角形全等书写三步骤:
①写出在哪两个三角形中
②摆出三个条件(注意:按定理名称的顺序书写)
③写出全等结论
证明的书写步骤:
若AB=AC,则添加什么条件可得ΔABD≌ΔACD
A
D
B
C
ΔABD≌ΔACD
S
A
S
AD=AD
AB=AC
∠BAD= ∠ CAD
巩固练习
若∠BAD= ∠CAD,则添加什么条件可使ΔABD≌ΔACD
A
B
D
C
ΔABD≌ΔACD
S
A
S
AD=AD
∠BAD= ∠ CAD
AB=AC
巩固练习
链接生活:
小明不小心打翻了墨水,将自己所画的三角形涂黑了,你能帮小明想想办法,画一个与原来完全一样的三角形吗?
小兰做了一个如图所示的风筝,其中∠EDH=∠FDH, ED=FD ,将上述条件标注在图中,小明不用测量就能知道EH=FH吗?与同桌进行交流。
E
F
D
H
解:在△EDH和△FDH中, ∵ ED=FD(已知)
∠EDH=∠FDH(已知)
DH=DH(公共边)
∴△EDH≌△FDH(S.A.S.)
是不是两条边和一个角对应相等的两个三角形就一定全等?你能举例说明吗?
回顾与思考
如果已知两个三角形有两边和一角对应相等时,应分为几种情形讨论?
边-角-边
边-边-角
A
A
A’
A’
B
B’
B
B’
C
C
C’
C’
以3cm、4cm为三角形的两边,长度3cm的边所对的角为45° ,情况又怎样?动手画一画,你发现了什么?
4cm
3cm
45°
A
3cm
步骤:
1.画一线段AC,使它等于4cm;
2.画∠ CAM= 45°;
3.以C为圆心, 3cm长为半径画弧,交AM于点B;
4.连结CB.
△ ABC 与 △ AB'C 就是所求做的三角形 .
显然: △ ABC与△ AB'C不全等
B
B’
M
C
结论:两边及其一边所对的角相等,两个三角形不一定全等.
1、今天我们学习哪种方法可以判定两个三角形全等?
边角边(S.A.S)
2、通过这节课我们知道,当两个三角形有两边和一角对应相等时不一定全等.
到了什么?
今天你学
说一说
全等三角形的性质是什么?
对应边相等;对应角相等。
如:△ABC≌△DEF,可以写出以下推理:
∵△ABC≌△DEF(已知)
∴AB=DE,BC=EF,AC=DF(全等三角形对应边相等)
∠A=∠D ,∠B=∠E,∠C=∠F
(全等三角形对应角相等)
A
B
C
D
E
F
回顾与思考
如果已知两个三角形有两边和一角对应相等时,应分为几种情形讨论?
边-角-边
边-边-角
A
A
A’
A’
B
B’
B
B’
C
C
C’
C’
温馨提示
做一做:画△ABC,使AB=3cm,AC=4cm.
画法:
1. 画线段AB= 3cm;
3. 在射线AM上截取AC=4cm;
这样画出来的三角形与同桌所画的三角形进行比较,它们互相重合吗?
若再加一个条件,使∠A=45°,画出△ABC.
2. 画∠MAB= 45°;
4. 连接BC.
△ABC就是所求的三角形.
把你们所画的三角形剪下来与同桌所画的三角形进行比较,它们能互相重合吗?
探究
用几何语言表达为:
在△ABC与△A`B`C`中
∴ △ABC≌△A`B`C`(SAS)
如果两个三角形有两边及其夹角分别对应相等,那么这两个三角形全等。简写成“边角边”或“SAS”
∵ AB=A`B`
∠B=∠B`
BC=B`C`
A
B
C
A`
B`
C`
如图△ABC和△ DEF 中,AB=DE=3 ㎝,∠ B=∠ E=300 , BC=EF=5 ㎝,它们完全重合吗?△ABC≌△ DEF吗 ?为什么
3㎝
5㎝
300
A
B
C
3㎝
5㎝
300
D
E
F
它们完全重合,即△ABC≌△ DEF .根据边角边.
分别找出各题中的全等三角形
A
B
C
40°
40°
D
E
F
(1)
D
C
A
B
(2)
△ABC≌△EFD 根据“SAS”
△ADC≌△CBA 根据“SAS”
平行四边形ABCD
如图,下列哪组条件不能判定△ABC≌△DEF( )
A
B
C
D
E
F
AB=DE
A、∠A=∠D
AC=DF
AC=DF
C、∠C=∠F
BC=EF
AB=DE
B、∠B=∠E
BC=EF
AC=DF
D、∠B=∠E
BC=EF
D
已知:如图,AB=CB,∠1=∠2 ,
△ABD 和△CBD 全等吗?为什么
例1
分析:
△ABD ≌△CBD
边AB=CB(已知)
角∠1= ∠2(已知)
边BD=BD(公共边)
A
B
C
D
(SAS)
解:在△ ABD 和△ CBD中,
∵ AB=CB(已知)
∠ABD=∠CBD(已知)
BD=BD(公共边)
∴△ABD ≌△CBD(SAS)
1
2
已知:如图,AD∥BC,AD=CB.
求证: △ADC≌△CBA
A
B
C
D
1
2
证明:∵AD∥BC
∴ ∠1=∠2(两直线平行,
内错角相等)
在△ADC和△CBA中
∵AD=CB(已知)
∠1=∠2(已证)
AC=CA(公共边)
∴ △ADC≌△CBA(SAS)
已知:如图,AD∥BC,AD=BC,AE=CF.
求证: △AFD≌△CEB
A
D
E
F
B
C
∵AD∥BC
∴ ∠A=∠C(两直线平行,内错角相等)
证明:∵AE=CF
∴AE+EF=CF+EF即AF=CE
在△ADF和△CEB中
∵ AD=CB(已知)
∠A=∠C(已证)
AF=CE(已证)
∴ △AFD≌△CEB(SAS)
已知:如图,AB=AC,AD=AE.
求证: △ABE≌△ACD
A
C
D
B
E
A
证明:在△ABE和△ACD中
∵ AB=AC(已知)
∠A=∠A(公共角)
AD=AE(已知)
∴ △ABE≌△ACD(SAS)
已知:如图,AB=AC,AD=AE, ∠1=∠2.
求证:△ADB≌△ACE
1
A
C
E
2
A
B
D
证明:∵∠1=∠2(已知)
∴ ∠1+∠BAE=∠2+∠BAE,
即∠CAE=∠BAD
在△ADB和△ACE中
∵ AB=AC(已知)
∠CAE=∠BAD(已证)
AD=AE(已知)
∴ △ADB≌△ACE(SAS)
A
B
C
D
O
如图AC与BD相交于点O,已知OA=OC,OB=OD,说明△AOB≌△COD的理由。
解:在△AOB和△COD中
∵ OA=OC(已知)
∠AOB=∠COD(对顶角)
OB=OD(已知)
∴ △AOB≌△COD(SAS)
1.准备条件:证全等时要用的条件 要先证好;
2.三角形全等书写三步骤:
①写出在哪两个三角形中
②摆出三个条件(注意:按定理名称的顺序书写)
③写出全等结论
证明的书写步骤:
若AB=AC,则添加什么条件可得ΔABD≌ΔACD
A
D
B
C
ΔABD≌ΔACD
S
A
S
AD=AD
AB=AC
∠BAD= ∠ CAD
巩固练习
若∠BAD= ∠CAD,则添加什么条件可使ΔABD≌ΔACD
A
B
D
C
ΔABD≌ΔACD
S
A
S
AD=AD
∠BAD= ∠ CAD
AB=AC
巩固练习
链接生活:
小明不小心打翻了墨水,将自己所画的三角形涂黑了,你能帮小明想想办法,画一个与原来完全一样的三角形吗?
小兰做了一个如图所示的风筝,其中∠EDH=∠FDH, ED=FD ,将上述条件标注在图中,小明不用测量就能知道EH=FH吗?与同桌进行交流。
E
F
D
H
解:在△EDH和△FDH中, ∵ ED=FD(已知)
∠EDH=∠FDH(已知)
DH=DH(公共边)
∴△EDH≌△FDH(S.A.S.)
是不是两条边和一个角对应相等的两个三角形就一定全等?你能举例说明吗?
回顾与思考
如果已知两个三角形有两边和一角对应相等时,应分为几种情形讨论?
边-角-边
边-边-角
A
A
A’
A’
B
B’
B
B’
C
C
C’
C’
以3cm、4cm为三角形的两边,长度3cm的边所对的角为45° ,情况又怎样?动手画一画,你发现了什么?
4cm
3cm
45°
A
3cm
步骤:
1.画一线段AC,使它等于4cm;
2.画∠ CAM= 45°;
3.以C为圆心, 3cm长为半径画弧,交AM于点B;
4.连结CB.
△ ABC 与 △ AB'C 就是所求做的三角形 .
显然: △ ABC与△ AB'C不全等
B
B’
M
C
结论:两边及其一边所对的角相等,两个三角形不一定全等.
1、今天我们学习哪种方法可以判定两个三角形全等?
边角边(S.A.S)
2、通过这节课我们知道,当两个三角形有两边和一角对应相等时不一定全等.
到了什么?
今天你学
说一说
