第3章 第2课时 函数的表示方法-高中数学人教A版(2019)必修第一册同步试题精编(Word含答案解析)
文档属性
| 名称 | 第3章 第2课时 函数的表示方法-高中数学人教A版(2019)必修第一册同步试题精编(Word含答案解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 663.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-31 00:00:00 | ||
图片预览


文档简介
函数的表示方法
学习目标:
1.掌握函数的三种表示方法,会正确表示函数;
2.会求不同问题背景下的函数的解析式,理解解析式求法蕴含的数学思想;
3.理解分段函数和复合函数,会求处理简单的分段函数与复合函数问题.
知识要点:
1.函数的表示方法
(1)解析法:用______表示两个变量之间的对应关系;
(2)列表法:列出____来表示两个变量之间的对应关系;
(3)图像法:用____图象表示两个变量之间的对应关系.
2.分段函数:函数在定义域的不同范围上有不同的_____即.
3.复合函数:形如形式的函数称为复合函数,其中称为____,称为内函数,
典型例题:
题组一 列表法及其应用
例1. 2015年以来,我国的年度数据如下表:
时间(年) 2015 2016 2017 2018 2019
GDP(万亿元) 68.5506 74.4127 82.7121 91.9281 99.0865
设时间为,与其对应的年度GDP为,那么( )
A.68.5506 B.74.4127 C.82.7121 D.91.9281
变式:对于函数,部分x与y的对应关系如下表:
x … 1 2 3 4 5 6 7 8 9 …
y … 3 7 5 9 6 1 8 2 4 …
数列满足:,且对于任意,点都在函数的图象上,则( )
A.7576 B.7575 C.7569 D.7564
题组二 图象法及其应用
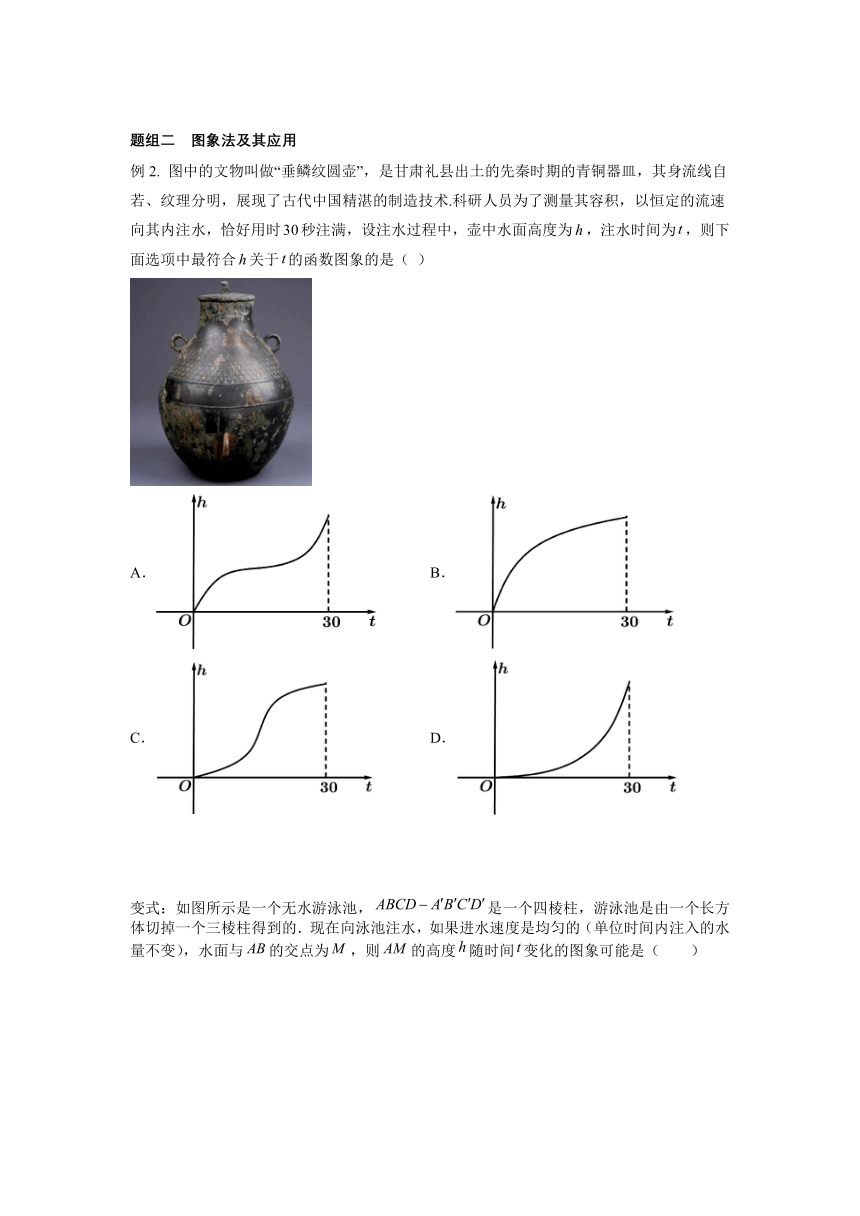
例2. 图中的文物叫做“垂鳞纹圆壶”,是甘肃礼县出土的先秦时期的青铜器皿,其身流线自若、纹理分明,展现了古代中国精湛的制造技术.科研人员为了测量其容积,以恒定的流速向其内注水,恰好用时秒注满,设注水过程中,壶中水面高度为,注水时间为,则下面选项中最符合关于的函数图象的是( )
A. B.
C. D.
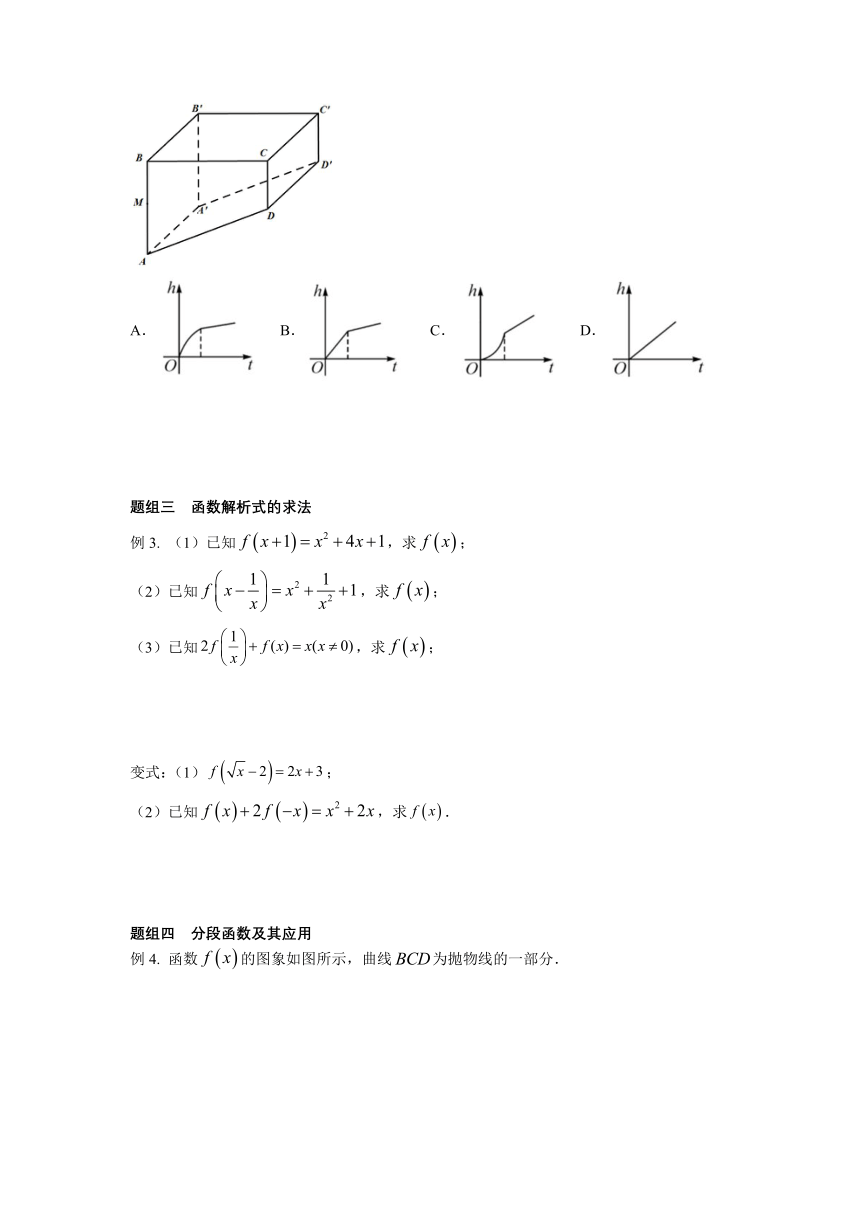
变式:如图所示是一个无水游泳池,是一个四棱柱,游泳池是由一个长方体切掉一个三棱柱得到的.现在向泳池注水,如果进水速度是均匀的(单位时间内注入的水量不变),水面与的交点为,则的高度随时间变化的图象可能是( )
A. B. C. D.
题组三 函数解析式的求法
例3. (1)已知,求;
(2)已知,求;
(3)已知,求;
变式:(1);
(2)已知,求.
题组四 分段函数及其应用
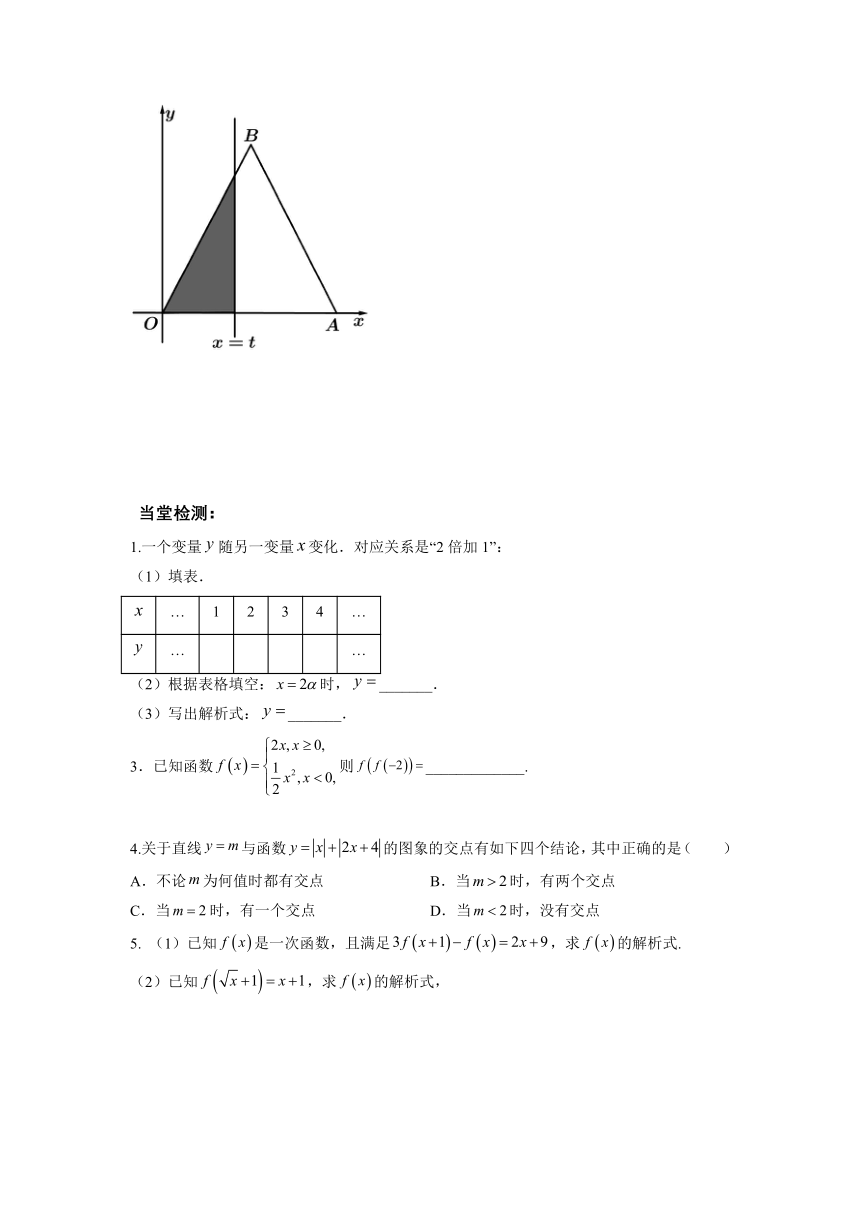
例4. 函数的图象如图所示,曲线为抛物线的一部分.
(Ⅰ)求解析式;
(Ⅱ)若,求的值;
变式:已知函数().
(1)用分段函数的形式表示该函数;
(2)画出该函数的图象;
(3)写出该函数的值域.
题组五 实际问题中的函数表示
例5.如图,把截面半径为25cm的圆形木头锯成矩形木料,如果矩形的一边长为cm,面积为cm2,把表示成的函数,并指出自变量的范围.
变式:如图,是边长为2的正三角形,记位于直线左侧的图形的面积为.试求函数的解析式,并画出函数的图象.
当堂检测:
1.一个变量随另一变量变化.对应关系是“2倍加1”:
(1)填表.
… 1 2 3 4 …
… …
(2)根据表格填空:时,_______.
(3)写出解析式:_______.
3.已知函数则_____________.
4.关于直线与函数的图象的交点有如下四个结论,其中正确的是( )
A.不论为何值时都有交点 B.当时,有两个交点
C.当时,有一个交点 D.当时,没有交点
5. (1)已知是一次函数,且满足,求的解析式.
(2)已知,求的解析式,
6.已知函数.
(1)试比较与的大小;
(2)画出函数的图象;
(3)若,求的值.
参考答案:
知识要点:
1.(1)解析式;(2)表格;(3)图象.
2.解析式
3.复合函数:外函数,
典型例题:
例1. D
解:由题意可得,
故选:D
变式:A
,,,,, ,
数列满足,
则.
故选:A.
例2. A
水壶的结构:低端与上端细、中间粗,
所以在注水恒定的情况下:
开始水的高度增加的快,中间增加的慢,最后水上升的速度又变快,
由图可知选项A符合,
故选:A
变式:A
由题意可知,当往游泳池内注水时,游泳池内的水呈“直棱柱”状,且直棱柱的高不变,
刚开始水面面积逐渐增大,水的高度增长得越来越慢,
当水面经过点后,水面的面积为定值,水的高度匀速增长,
故符合条件的函数图象为A选项中的图象.
故选:A.
例3.(1),
令,则,
,
;
(2),
;
(3),将原式中的x与互换,得.
于是得关于f(x)的方程组
解得.
变式:(1)设,则,得,
则
所以;
(2)∵,
将x换成-x,得,
∴将以上两式消去,得,∴.
例4. (1)当,函数图象为直线且过点,所以;
当时,函数图象为抛物线,设函数解析式为,
当时,,解得,所以,
所以.
(2)当时,令,解得;
当时,令,解得 ,
因为,所以,
所以或;
变式:(1)当时,;当时,.
∴
(2)函数的图象如图所示,
(3)由(1)知,在上的值域为.
例5.因为半径为25cm, 矩形的一边长为x cm,则矩形另一边为,所以矩形面积,由于矩形内接于圆,所以其边长的范围是:,把y表示成x的函数为:,.
变式:(1)当时,
如图,设直线与分别交于、两点,则,
又,,
(2)当时,
如图,设直线与分别交于、两点,则,
又,,
,
(3)当时,,
综上所述,
当堂检测:
1.(2);(3)y=2x+1.
解:(1)因为变量y随另一变量x变化,对应关系是“2倍加1”:
完整的表格如表所示:
x … 1 2 3 4 …
y … 3 5 7 9 …
(2)根据表格填空:时,;
(3)根据题意,函数的解析式:y=2x+1.
故答案为:(1)填表见解析;(2);(3)2x+1.
3.4
∵,∴,又∵,∴,∴.
故答案为:4.
4.BCD
由题意得,,作此函数图像如下图折线所示;即平行于轴的直线,作图像如下图直线所示.
对于A,由图可知,当时,直线与函数的图象无交点,故A错误;
对于B,由图可知,当时,直线与函数的图象有两个交点,故B正确;
对于C,由图可知,当时,直线与函数的图象,有一个交点,故C正确;
对于D,由图可知,当时,直线与函数的图象无交点,故D正确.
故选:BCD
5.(1);(2).
(1)因为是一次函数,所以设,又因为,所以,整理得,故,解得,所以;
(2)令,则,所以,即.
6.解:(1)∵,∴,
又∵,∴,
∵,∴,∴,
所以.
(2)图象如图所示,
(3)当时,有,解得;
当时,有,解得
或,
但,故舍去,所以的值为3,
综上所述:的值为或3.
学习目标:
1.掌握函数的三种表示方法,会正确表示函数;
2.会求不同问题背景下的函数的解析式,理解解析式求法蕴含的数学思想;
3.理解分段函数和复合函数,会求处理简单的分段函数与复合函数问题.
知识要点:
1.函数的表示方法
(1)解析法:用______表示两个变量之间的对应关系;
(2)列表法:列出____来表示两个变量之间的对应关系;
(3)图像法:用____图象表示两个变量之间的对应关系.
2.分段函数:函数在定义域的不同范围上有不同的_____即.
3.复合函数:形如形式的函数称为复合函数,其中称为____,称为内函数,
典型例题:
题组一 列表法及其应用
例1. 2015年以来,我国的年度数据如下表:
时间(年) 2015 2016 2017 2018 2019
GDP(万亿元) 68.5506 74.4127 82.7121 91.9281 99.0865
设时间为,与其对应的年度GDP为,那么( )
A.68.5506 B.74.4127 C.82.7121 D.91.9281
变式:对于函数,部分x与y的对应关系如下表:
x … 1 2 3 4 5 6 7 8 9 …
y … 3 7 5 9 6 1 8 2 4 …
数列满足:,且对于任意,点都在函数的图象上,则( )
A.7576 B.7575 C.7569 D.7564
题组二 图象法及其应用
例2. 图中的文物叫做“垂鳞纹圆壶”,是甘肃礼县出土的先秦时期的青铜器皿,其身流线自若、纹理分明,展现了古代中国精湛的制造技术.科研人员为了测量其容积,以恒定的流速向其内注水,恰好用时秒注满,设注水过程中,壶中水面高度为,注水时间为,则下面选项中最符合关于的函数图象的是( )
A. B.
C. D.
变式:如图所示是一个无水游泳池,是一个四棱柱,游泳池是由一个长方体切掉一个三棱柱得到的.现在向泳池注水,如果进水速度是均匀的(单位时间内注入的水量不变),水面与的交点为,则的高度随时间变化的图象可能是( )
A. B. C. D.
题组三 函数解析式的求法
例3. (1)已知,求;
(2)已知,求;
(3)已知,求;
变式:(1);
(2)已知,求.
题组四 分段函数及其应用
例4. 函数的图象如图所示,曲线为抛物线的一部分.
(Ⅰ)求解析式;
(Ⅱ)若,求的值;
变式:已知函数().
(1)用分段函数的形式表示该函数;
(2)画出该函数的图象;
(3)写出该函数的值域.
题组五 实际问题中的函数表示
例5.如图,把截面半径为25cm的圆形木头锯成矩形木料,如果矩形的一边长为cm,面积为cm2,把表示成的函数,并指出自变量的范围.
变式:如图,是边长为2的正三角形,记位于直线左侧的图形的面积为.试求函数的解析式,并画出函数的图象.
当堂检测:
1.一个变量随另一变量变化.对应关系是“2倍加1”:
(1)填表.
… 1 2 3 4 …
… …
(2)根据表格填空:时,_______.
(3)写出解析式:_______.
3.已知函数则_____________.
4.关于直线与函数的图象的交点有如下四个结论,其中正确的是( )
A.不论为何值时都有交点 B.当时,有两个交点
C.当时,有一个交点 D.当时,没有交点
5. (1)已知是一次函数,且满足,求的解析式.
(2)已知,求的解析式,
6.已知函数.
(1)试比较与的大小;
(2)画出函数的图象;
(3)若,求的值.
参考答案:
知识要点:
1.(1)解析式;(2)表格;(3)图象.
2.解析式
3.复合函数:外函数,
典型例题:
例1. D
解:由题意可得,
故选:D
变式:A
,,,,, ,
数列满足,
则.
故选:A.
例2. A
水壶的结构:低端与上端细、中间粗,
所以在注水恒定的情况下:
开始水的高度增加的快,中间增加的慢,最后水上升的速度又变快,
由图可知选项A符合,
故选:A
变式:A
由题意可知,当往游泳池内注水时,游泳池内的水呈“直棱柱”状,且直棱柱的高不变,
刚开始水面面积逐渐增大,水的高度增长得越来越慢,
当水面经过点后,水面的面积为定值,水的高度匀速增长,
故符合条件的函数图象为A选项中的图象.
故选:A.
例3.(1),
令,则,
,
;
(2),
;
(3),将原式中的x与互换,得.
于是得关于f(x)的方程组
解得.
变式:(1)设,则,得,
则
所以;
(2)∵,
将x换成-x,得,
∴将以上两式消去,得,∴.
例4. (1)当,函数图象为直线且过点,所以;
当时,函数图象为抛物线,设函数解析式为,
当时,,解得,所以,
所以.
(2)当时,令,解得;
当时,令,解得 ,
因为,所以,
所以或;
变式:(1)当时,;当时,.
∴
(2)函数的图象如图所示,
(3)由(1)知,在上的值域为.
例5.因为半径为25cm, 矩形的一边长为x cm,则矩形另一边为,所以矩形面积,由于矩形内接于圆,所以其边长的范围是:,把y表示成x的函数为:,.
变式:(1)当时,
如图,设直线与分别交于、两点,则,
又,,
(2)当时,
如图,设直线与分别交于、两点,则,
又,,
,
(3)当时,,
综上所述,
当堂检测:
1.(2);(3)y=2x+1.
解:(1)因为变量y随另一变量x变化,对应关系是“2倍加1”:
完整的表格如表所示:
x … 1 2 3 4 …
y … 3 5 7 9 …
(2)根据表格填空:时,;
(3)根据题意,函数的解析式:y=2x+1.
故答案为:(1)填表见解析;(2);(3)2x+1.
3.4
∵,∴,又∵,∴,∴.
故答案为:4.
4.BCD
由题意得,,作此函数图像如下图折线所示;即平行于轴的直线,作图像如下图直线所示.
对于A,由图可知,当时,直线与函数的图象无交点,故A错误;
对于B,由图可知,当时,直线与函数的图象有两个交点,故B正确;
对于C,由图可知,当时,直线与函数的图象,有一个交点,故C正确;
对于D,由图可知,当时,直线与函数的图象无交点,故D正确.
故选:BCD
5.(1);(2).
(1)因为是一次函数,所以设,又因为,所以,整理得,故,解得,所以;
(2)令,则,所以,即.
6.解:(1)∵,∴,
又∵,∴,
∵,∴,∴,
所以.
(2)图象如图所示,
(3)当时,有,解得;
当时,有,解得
或,
但,故舍去,所以的值为3,
综上所述:的值为或3.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
