2021-2022学年人教版八年级上册数学15.3 分式方程 专题训练(word版含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级上册数学15.3 分式方程 专题训练(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 251.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-31 16:37:49 | ||
图片预览


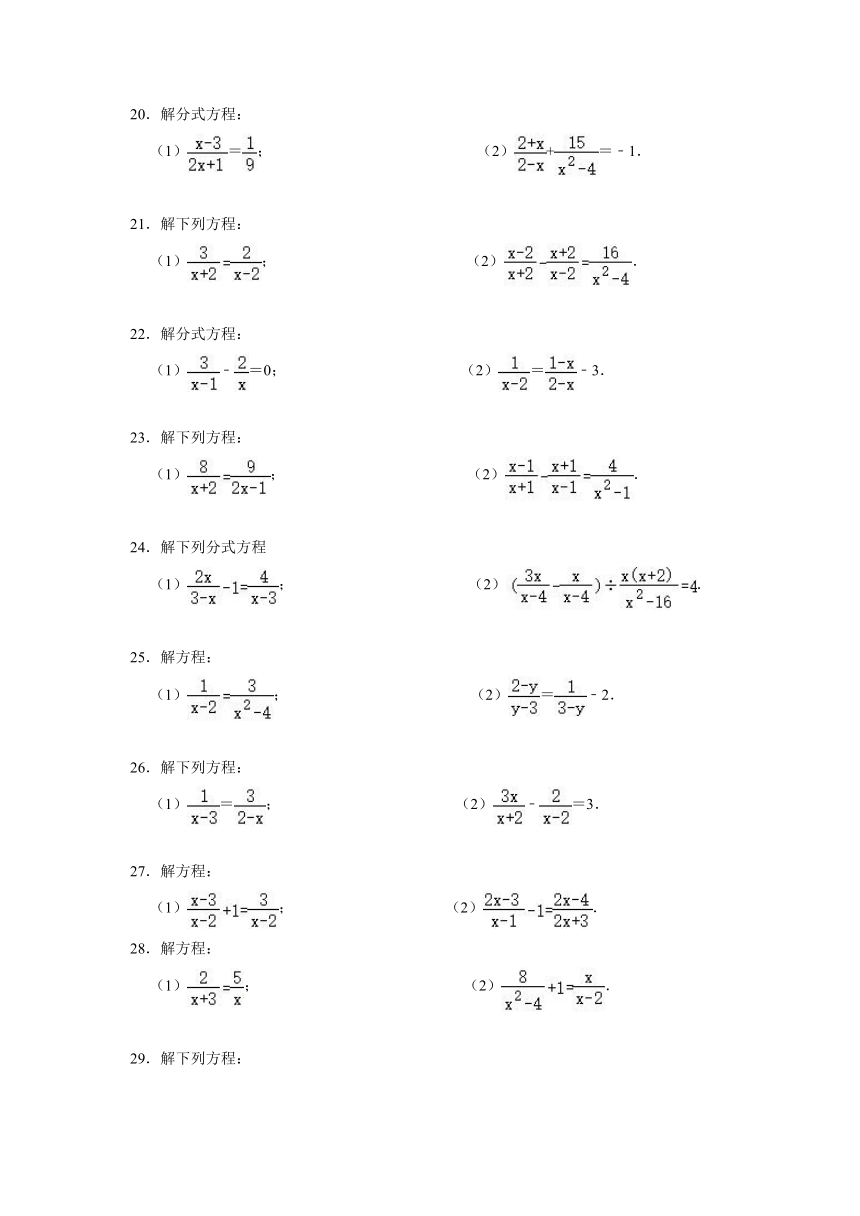


文档简介
15.3分式方程专题训练(附答案)
1.解方程:
(1); (2).
2.解分式方程:
(1)﹣1=; (2)=﹣2.
3.解方程:
(1)﹣=; (2)﹣=1.
4.解分式方程:
(1)=; (2)=1.
5.解分式方程:
(1)2=; (2)=1.
6.解分式方程:
(1). (2).
7.解分式方程:
(1)=; (2)=﹣2.
8.解方程:
(1); (2).
9.(1)解方程:=1; (2)计算:.
10.(1)化简:﹣; (2)解方程:﹣1=.
11.解方程:
(1)+=4; (2)=2﹣.
12.解分式方程:
(1)﹣1=; (2)=.
13.解分式方程:
(1)﹣=2; (2)+=.
14.解方程:
(1)﹣=1. (2)﹣1=.
15.解方程:
(1); (2).
16.解方程:
(1)+=1; (2)+1=.
17.解分式方程:
(1)﹣=2; (2)﹣1=.
18.解方程:
(1)=; (2)=+2.
19.解下列分式方程:
(1)+=1; (2)﹣1=.
20.解分式方程:
(1)=; (2)+=﹣1.
21.解下列方程:
(1); (2).
22.解分式方程:
(1)﹣=0; (2)=﹣3.
23.解下列方程:
(1); (2).
24.解下列分式方程
(1); (2).
25.解方程:
(1); (2)=﹣2.
26.解下列方程:
(1)=; (2)﹣=3.
27.解方程:
(1); (2).
28.解方程:
(1); (2).
29.解下列方程:
(1); (2).
30.某同学解方程﹣2=,过程如下:
第一步:整理,得﹣2=,
第二步:….
(1)请你说明第一步变化过程的依据是: ;
(2)请把以上解方程的过程补充完整.
参考答案
1.解:(1)去分母得,x(x+1)=4+x2﹣1,
解得:x=3,
检验:把x=3代入得:(x+1)(x﹣1)≠0,
所以,原方程的根为:x=3;
(2)去分母,得2x=3(x﹣2),
去括号,得2x=3x﹣6,
移项,合并同类项,得﹣x=﹣6,
化x的系数为1,得x=6,
检验:把x=6代入得:x(x﹣2)≠0,
∴原方程的解为x=6.
2.(1)解:﹣1=,
﹣1=,
x(x+2)﹣(x+2)(x﹣2)=6,
x2+2x﹣x2+4=6,
2x=2,
x=1,
检验:把x=1代入(x+2)(x﹣2)≠0,
∴原方程的解是x=1.
(2)=﹣2,
=﹣2,
2﹣x=﹣1﹣2(x﹣3),
2﹣x=﹣1﹣2x+6,
﹣x+2x=﹣1+6﹣2,
x=3,
检验:把x=3代入(x﹣3)=0,
x=3不是原方程的解,
∴原方程无解.
3.解:(1)去分母得:3(3x﹣1)﹣2=5,
去括号得:9x﹣3﹣2=5,
移项合并得:9x=10,
解得:x=,
检验:把x=代入得:2(3x﹣1)≠0,
∴x=是分式方程的解;
(2)去分母得:x(x+2)﹣3=(x﹣1)(x+2),
整理得:x2+2x﹣3=x2+x﹣2,
解得:x=1,
检验:把x=1代入得:(x﹣1)(x+2)=0,
∴x=1是增根,分式方程无解.
4.解:(1)去分母得:3(x+1)=2x+3,
去括号得:3x+3=2x+3,
解得:x=0,
检验:把x=0代入得:(2x+3)(x+1)=3≠0,
∴x=0是分式方程的解;
(2)去分母得:3+x(x+3)=x2﹣9,
整理得:3+x2+3x=x2﹣9,
解得:x=﹣4,
检验:把x=﹣4代入得:(x+3)(x﹣3)=7≠0,
∴x=﹣4是分式方程的解.
5.解:(1),
去分母得:3+2(x﹣1)=x,
解得,x=﹣1,
检验:当x=﹣1时,x﹣1≠0,
∴原方程的解为:x=﹣1;
(2)=1,
去分母得:x2﹣4x+4﹣3x=x2﹣2x,
解得:x=,
检验:当x=时,x(x﹣2)≠0,
∴x=是分式方程的解.
6.解:(1)方程两边同乘(x﹣5),
得3﹣x+5=2x﹣1,
解得x=3,
经检验,x=3是原方程的解;
(2)方程两边同乘(x﹣5)(x+2),
得12﹣(x﹣1)(x﹣2)=(6﹣x)(x+2),
解得x=﹣2,
经检验,x=﹣2是增根,原方程无解.
7.解:(1)方程两边都乘(x+1)(x﹣1),得2(x+1)=5,
解得x=,
检验:当x=时,(x+1)(x﹣1)≠0,
所以分式方程的解为x=.
(2)方程两边都乘(x﹣2),得1﹣x=﹣1﹣2(x﹣2),
解得x=2,
检验:当x=2时,x﹣2=0,
所以x=2是增根,原方程无解.
8.解:(1)方程两边同乘以x2﹣4,得x+2=3,
解得x=1,
检验:当x=1时,x2﹣4=﹣3≠0,
∴x=1原分式方程的解;
(2)方程两边同乘以2x﹣1,得x=2x﹣1+3,
解得x=﹣2,
检验:当x=﹣2时,2x﹣1=﹣5≠0,
∴x=﹣2原分式方程的解.
9.解:(1)去分母得:(x﹣2)2﹣16=x2﹣4,
解得:x=﹣2,
检验:把x=﹣2代入得:(x+2)(x﹣2)=0,
∴x=﹣2是增根,分式方程无解;
(2)原式=
=
=.
10.解:(1)原式=+=;
(2)去分母得:6x﹣3x+3=x,
解得:x=﹣,
检验:把x=﹣代入得:x﹣1≠0,
∴分式方程的解为x=﹣.
11.解:(1)方程两边同时乘以(2x﹣3)得:x﹣5=4(2x﹣3),
解得:x=1,
把x=1代入2x﹣3得:2×1﹣3≠0,
∴x=1是原方程的解;
(2)方程两边同时乘以(x﹣3)得:x﹣2=2(x﹣3)+1,
解得:x=3,
把x=3代入x﹣3得:3﹣3=0,
∴x=3是分式方程的增根,原方程无解.
12.解:(1),
,
方程两边都乘2x﹣5,
得x﹣(2x﹣5)=﹣5,
x﹣2x+5=﹣5,
解这个方程,
得x=10,
经检验,x=10是原方程的根.
(2),
方程两边都乘以(x+4)(x﹣4),
得x+4=4,
解这个方程,得x=0,
经检验,x=0是原方程的根.
13.解:(1)
方程两边都乘2x﹣2,得1+2x=4x﹣4,
解这个方程,得,
检验,当x=时,2x﹣2≠0,
所以是原方程的根,
即原方程的解是x=;
(2),
﹣=,
方程两边都乘(x+1)(x﹣1),得x﹣1﹣2x=3(x+1),
解这个方程,得x=﹣1,
经检验,x=﹣1是原方程的增根,
所以原方程无解.
14.解:(1)﹣=1,
方程两边都乘x(x﹣2),得:(x+3)(x﹣2)﹣2x=x(x﹣2),
去括号,得:x2+x﹣6﹣2x=x2﹣2x,
解得:x=6,
检验:当x=6时,x﹣2≠0,
∴原方程的解是x=6;
(2)﹣1=,
方程两边都乘(x﹣1)(x+1),得:(x+1)2﹣(x2﹣1)=4,
去括号,得:x2+2x+1﹣x2+1=4,
移项、合并同类项,得:2x=2,
解得:x=1,
检验:当x=1时,x﹣1=0,
∴原方程无解.
15.解:(1)给分式方程两边同时乘以x(x﹣3),
得7x=5(x﹣3),
2x=﹣15,
解得x=﹣,
把x=﹣代入x(x﹣3)≠0,
所以x=﹣是原分式方程的解;
(2),
给分式方程两边同时乘以x﹣2,
得1﹣2x=2(x﹣2)﹣3,
解得x=2,
把x=2代入x﹣2=0,
所以原分式方程无解.
16.解:(1)去分母得:2﹣x﹣1=x﹣3,
解得:x=2,
检验:把x=2代入得:x﹣3=2﹣3=﹣1≠0,
∴分式方程的解为x=2;
(2)去分母得:x﹣2+2x﹣1=﹣1.5,
解得:x=0.5,
检验:把x=0.5代入得:2x﹣1=1﹣1=0,
∴x=0.5是增根,分式方程无解.
17.解:(1)去分母得:x+1+4=2x﹣6,
解得:x=11,
检验:当x=11时,x﹣3≠0,
所以x=11是原方程的解;
(2)去分母得:x(x+2)﹣(x+2)(x﹣2)=8,
解得:x=2,
经检验x=2是原方程的增根,
所以原分式方程无解
18.解:(1)方程两边同时乘(2x﹣1)(x+3),可得:3(x+3)=3(2x﹣1),
解得x=4,
检验:当x=4时,(2x﹣1)(x+3)≠0,
∴原分式方程的解为x=4.
(2)方程两边同时乘3(x﹣3),可得:2x+9=3(4x﹣7)+6(x﹣3)
解得x=3,
检验:当x=3时,3(x﹣3)=0,
∴x=3不是原分式方程的解,
∴原分式方程无解.
19.解:(1)∵+=1,
∴﹣=1,
方程两边同时乘(x﹣1),可得:1﹣2=x﹣1,
解得x=0,x﹣1≠0,
∴原分式方程的解为x=0.
(2)∵﹣1=,
∴﹣1=,
方程两边同时乘(x+2)(x﹣2),可得:x(x+2)﹣(x+2)(x﹣2)=8,
整理得:2x﹣4=0,
解得x=2,
检验:当x=2时,(x+2)(x﹣2)=0,
∴原分式方程无解.
20.解:(1)=,
方程两边都乘以9(2x+1),得9(x﹣3)=2x+1,
解得:x=4,
检验:当x=4时,9(2x+1)≠0,所以x=4是原方程的解,
即原方程的解是x=4;
(2)原方程化为:+=﹣1,
方程两边都乘以(x+2)(x﹣2),得﹣(x+2)2+15=﹣(x+2)(x﹣2),
解得:x=,
检验:当x=时,(x+2)(x﹣2)≠0,所以x=是原方程的解,
即原方程的解是x=.
21.解:(1),
去分母得,3(x﹣2)=2(x+2),
去括号得,3x﹣6=2x+4,
移项得,x=10,
经检验:x=10为方程的解,
∴方程的解为x=10;
(2),
去分母得,(x﹣2)2﹣(x+2)2=16,
去括号得,﹣8x=16,
两边同时除以﹣8得,x=﹣2,
经检验:x=﹣2为方程的增根,
∴原方程无解.
22.解:(1)﹣=0,
去分母得,3x﹣2(x﹣1)=0,
去括号得,x=﹣2,
经检验:x=﹣2是方程的根,
∴x=﹣2是原方程的解;
(2)=﹣3,
去分母得,1=﹣(1﹣x)﹣3(x﹣2),
去括号得,1=﹣1+x﹣3x+6,
解得:x=2,
检验:x=2是增根,
∴原方程无解.
23.解:(1)去分母得:8(2x﹣1)=9(x+2),
去括号得:16x﹣8=9x+18,
化简得:7x=26,
∴x=,
检验:当x=时,(x+2)(2x﹣1)≠0,
∴原方程的解为x=;
(2)去分母得:(x﹣1)2﹣(x+1)2=4,
去括号得:x2﹣2x+1﹣x2﹣2x﹣1=4,
化简得:﹣4x=4,
∴x=﹣1,
检验:当x=﹣1时,(x+1)(x﹣1)=0,
∴x=﹣1是增根,原方程无解.
24.解:(1)整理,得:,
去分母,得:﹣2x﹣(x﹣3)=4,
解得:x=﹣,
经检验:当x=﹣时,x﹣3≠0,
∴x=﹣是原分式方程的解,
(2)整理,得:,
,
去分母,得:2(x+4)=4(x+2),
解得:x=0,
经检验:当x=0时,(x+4)(x﹣4)≠0,x(x+2)=0,
∴x=0是原方程的增根,
原分式方程无解.
25.(1)解:方程两边同时乘以(x+2)(x﹣2),得,
x+2=3,
解得x=1,
经检验,x=1是原方程的解,
∴原方程的解为x=1.
(2)解:方程两边同时乘以(y﹣3)得,
2﹣y=﹣1﹣2(y﹣3),
解得y=3,
当y=3时,y﹣3=0,
∴原方程无解
26.解:(1)去分母得:2﹣x=3(x﹣3),
去括号得:2﹣x=3x﹣9,
解得:x=,
检验:当x=时,(x﹣3)(2﹣x)≠0,
∴分式方程的解为x=;
(2)去分母得:3x(x﹣2)﹣2(x+2)=3(x+2)(x﹣2),
整理得:3x2﹣6x﹣2x﹣4=3x2﹣12,
移项合并得:﹣8x=﹣8,
解得:x=1,
检验:当x=1时,(x+2)(x﹣2)≠0,
∴分式方程的解为x=1.
27.解:(1)方程两边同时乘以x﹣2得x﹣3+x﹣2=3,
解整式方程得,x=4,
检验:当x=4时,x﹣2≠0
∴x=4是原方程的解.
(2)方程两边同时乘以(x﹣1)(2x+3)得:2x2﹣x﹣6=2(x﹣2)(x﹣1),
整理得:5x=10,
解得:x=2,
检验:当x=2时,(x﹣1)(2x+3)≠0,
∴分式方程的解为x=2.
28.解:(1)去分母得:2x=5(x+3),
解得:x=﹣5
检验:x=﹣5时,x(x+3)≠0,
∴x=﹣5是原方程的解;
(2)去分母得:8+x2﹣4=x (x+2),
解得:x=2,
检验:当x=2时,(x+2)(x﹣2)=0,
∴x=2 是增根,原方程无解.
29.解:(1)去分母得:2x=3x﹣9,
解得:x=9,
检验:当x=9时,x(x﹣3)≠0,
∴分式方程的解为x=9;
(2)去分母得:4=(x+2)(x+1)﹣(x2﹣1),
去括号得:4=(x+2)(x+1)﹣x2+1,
整理得:4=x2+3x+2﹣x2+1,
解得:x=,
检验:当x=时,(x+1)(x﹣1)≠0,
∴分式方程的解为x=.
30.解:(1)由题意可得:第一步变化过程的依据是:分式的基本性质,
故答案为:分式的基本性质;
(2)方程两边同乘(x﹣3)得:x﹣2﹣2(x﹣3)=10﹣3x,
去括号,得:x﹣2﹣2x+6=10﹣3x,
移项,得:x﹣2x+3x=10﹣6+2,
合并同类项,得:2x=6,
系数化1,得:x=3,
检验:当x=3时,x﹣3=0,
∴x=3是原方程的增根,
∴原分式方程无解.
1.解方程:
(1); (2).
2.解分式方程:
(1)﹣1=; (2)=﹣2.
3.解方程:
(1)﹣=; (2)﹣=1.
4.解分式方程:
(1)=; (2)=1.
5.解分式方程:
(1)2=; (2)=1.
6.解分式方程:
(1). (2).
7.解分式方程:
(1)=; (2)=﹣2.
8.解方程:
(1); (2).
9.(1)解方程:=1; (2)计算:.
10.(1)化简:﹣; (2)解方程:﹣1=.
11.解方程:
(1)+=4; (2)=2﹣.
12.解分式方程:
(1)﹣1=; (2)=.
13.解分式方程:
(1)﹣=2; (2)+=.
14.解方程:
(1)﹣=1. (2)﹣1=.
15.解方程:
(1); (2).
16.解方程:
(1)+=1; (2)+1=.
17.解分式方程:
(1)﹣=2; (2)﹣1=.
18.解方程:
(1)=; (2)=+2.
19.解下列分式方程:
(1)+=1; (2)﹣1=.
20.解分式方程:
(1)=; (2)+=﹣1.
21.解下列方程:
(1); (2).
22.解分式方程:
(1)﹣=0; (2)=﹣3.
23.解下列方程:
(1); (2).
24.解下列分式方程
(1); (2).
25.解方程:
(1); (2)=﹣2.
26.解下列方程:
(1)=; (2)﹣=3.
27.解方程:
(1); (2).
28.解方程:
(1); (2).
29.解下列方程:
(1); (2).
30.某同学解方程﹣2=,过程如下:
第一步:整理,得﹣2=,
第二步:….
(1)请你说明第一步变化过程的依据是: ;
(2)请把以上解方程的过程补充完整.
参考答案
1.解:(1)去分母得,x(x+1)=4+x2﹣1,
解得:x=3,
检验:把x=3代入得:(x+1)(x﹣1)≠0,
所以,原方程的根为:x=3;
(2)去分母,得2x=3(x﹣2),
去括号,得2x=3x﹣6,
移项,合并同类项,得﹣x=﹣6,
化x的系数为1,得x=6,
检验:把x=6代入得:x(x﹣2)≠0,
∴原方程的解为x=6.
2.(1)解:﹣1=,
﹣1=,
x(x+2)﹣(x+2)(x﹣2)=6,
x2+2x﹣x2+4=6,
2x=2,
x=1,
检验:把x=1代入(x+2)(x﹣2)≠0,
∴原方程的解是x=1.
(2)=﹣2,
=﹣2,
2﹣x=﹣1﹣2(x﹣3),
2﹣x=﹣1﹣2x+6,
﹣x+2x=﹣1+6﹣2,
x=3,
检验:把x=3代入(x﹣3)=0,
x=3不是原方程的解,
∴原方程无解.
3.解:(1)去分母得:3(3x﹣1)﹣2=5,
去括号得:9x﹣3﹣2=5,
移项合并得:9x=10,
解得:x=,
检验:把x=代入得:2(3x﹣1)≠0,
∴x=是分式方程的解;
(2)去分母得:x(x+2)﹣3=(x﹣1)(x+2),
整理得:x2+2x﹣3=x2+x﹣2,
解得:x=1,
检验:把x=1代入得:(x﹣1)(x+2)=0,
∴x=1是增根,分式方程无解.
4.解:(1)去分母得:3(x+1)=2x+3,
去括号得:3x+3=2x+3,
解得:x=0,
检验:把x=0代入得:(2x+3)(x+1)=3≠0,
∴x=0是分式方程的解;
(2)去分母得:3+x(x+3)=x2﹣9,
整理得:3+x2+3x=x2﹣9,
解得:x=﹣4,
检验:把x=﹣4代入得:(x+3)(x﹣3)=7≠0,
∴x=﹣4是分式方程的解.
5.解:(1),
去分母得:3+2(x﹣1)=x,
解得,x=﹣1,
检验:当x=﹣1时,x﹣1≠0,
∴原方程的解为:x=﹣1;
(2)=1,
去分母得:x2﹣4x+4﹣3x=x2﹣2x,
解得:x=,
检验:当x=时,x(x﹣2)≠0,
∴x=是分式方程的解.
6.解:(1)方程两边同乘(x﹣5),
得3﹣x+5=2x﹣1,
解得x=3,
经检验,x=3是原方程的解;
(2)方程两边同乘(x﹣5)(x+2),
得12﹣(x﹣1)(x﹣2)=(6﹣x)(x+2),
解得x=﹣2,
经检验,x=﹣2是增根,原方程无解.
7.解:(1)方程两边都乘(x+1)(x﹣1),得2(x+1)=5,
解得x=,
检验:当x=时,(x+1)(x﹣1)≠0,
所以分式方程的解为x=.
(2)方程两边都乘(x﹣2),得1﹣x=﹣1﹣2(x﹣2),
解得x=2,
检验:当x=2时,x﹣2=0,
所以x=2是增根,原方程无解.
8.解:(1)方程两边同乘以x2﹣4,得x+2=3,
解得x=1,
检验:当x=1时,x2﹣4=﹣3≠0,
∴x=1原分式方程的解;
(2)方程两边同乘以2x﹣1,得x=2x﹣1+3,
解得x=﹣2,
检验:当x=﹣2时,2x﹣1=﹣5≠0,
∴x=﹣2原分式方程的解.
9.解:(1)去分母得:(x﹣2)2﹣16=x2﹣4,
解得:x=﹣2,
检验:把x=﹣2代入得:(x+2)(x﹣2)=0,
∴x=﹣2是增根,分式方程无解;
(2)原式=
=
=.
10.解:(1)原式=+=;
(2)去分母得:6x﹣3x+3=x,
解得:x=﹣,
检验:把x=﹣代入得:x﹣1≠0,
∴分式方程的解为x=﹣.
11.解:(1)方程两边同时乘以(2x﹣3)得:x﹣5=4(2x﹣3),
解得:x=1,
把x=1代入2x﹣3得:2×1﹣3≠0,
∴x=1是原方程的解;
(2)方程两边同时乘以(x﹣3)得:x﹣2=2(x﹣3)+1,
解得:x=3,
把x=3代入x﹣3得:3﹣3=0,
∴x=3是分式方程的增根,原方程无解.
12.解:(1),
,
方程两边都乘2x﹣5,
得x﹣(2x﹣5)=﹣5,
x﹣2x+5=﹣5,
解这个方程,
得x=10,
经检验,x=10是原方程的根.
(2),
方程两边都乘以(x+4)(x﹣4),
得x+4=4,
解这个方程,得x=0,
经检验,x=0是原方程的根.
13.解:(1)
方程两边都乘2x﹣2,得1+2x=4x﹣4,
解这个方程,得,
检验,当x=时,2x﹣2≠0,
所以是原方程的根,
即原方程的解是x=;
(2),
﹣=,
方程两边都乘(x+1)(x﹣1),得x﹣1﹣2x=3(x+1),
解这个方程,得x=﹣1,
经检验,x=﹣1是原方程的增根,
所以原方程无解.
14.解:(1)﹣=1,
方程两边都乘x(x﹣2),得:(x+3)(x﹣2)﹣2x=x(x﹣2),
去括号,得:x2+x﹣6﹣2x=x2﹣2x,
解得:x=6,
检验:当x=6时,x﹣2≠0,
∴原方程的解是x=6;
(2)﹣1=,
方程两边都乘(x﹣1)(x+1),得:(x+1)2﹣(x2﹣1)=4,
去括号,得:x2+2x+1﹣x2+1=4,
移项、合并同类项,得:2x=2,
解得:x=1,
检验:当x=1时,x﹣1=0,
∴原方程无解.
15.解:(1)给分式方程两边同时乘以x(x﹣3),
得7x=5(x﹣3),
2x=﹣15,
解得x=﹣,
把x=﹣代入x(x﹣3)≠0,
所以x=﹣是原分式方程的解;
(2),
给分式方程两边同时乘以x﹣2,
得1﹣2x=2(x﹣2)﹣3,
解得x=2,
把x=2代入x﹣2=0,
所以原分式方程无解.
16.解:(1)去分母得:2﹣x﹣1=x﹣3,
解得:x=2,
检验:把x=2代入得:x﹣3=2﹣3=﹣1≠0,
∴分式方程的解为x=2;
(2)去分母得:x﹣2+2x﹣1=﹣1.5,
解得:x=0.5,
检验:把x=0.5代入得:2x﹣1=1﹣1=0,
∴x=0.5是增根,分式方程无解.
17.解:(1)去分母得:x+1+4=2x﹣6,
解得:x=11,
检验:当x=11时,x﹣3≠0,
所以x=11是原方程的解;
(2)去分母得:x(x+2)﹣(x+2)(x﹣2)=8,
解得:x=2,
经检验x=2是原方程的增根,
所以原分式方程无解
18.解:(1)方程两边同时乘(2x﹣1)(x+3),可得:3(x+3)=3(2x﹣1),
解得x=4,
检验:当x=4时,(2x﹣1)(x+3)≠0,
∴原分式方程的解为x=4.
(2)方程两边同时乘3(x﹣3),可得:2x+9=3(4x﹣7)+6(x﹣3)
解得x=3,
检验:当x=3时,3(x﹣3)=0,
∴x=3不是原分式方程的解,
∴原分式方程无解.
19.解:(1)∵+=1,
∴﹣=1,
方程两边同时乘(x﹣1),可得:1﹣2=x﹣1,
解得x=0,x﹣1≠0,
∴原分式方程的解为x=0.
(2)∵﹣1=,
∴﹣1=,
方程两边同时乘(x+2)(x﹣2),可得:x(x+2)﹣(x+2)(x﹣2)=8,
整理得:2x﹣4=0,
解得x=2,
检验:当x=2时,(x+2)(x﹣2)=0,
∴原分式方程无解.
20.解:(1)=,
方程两边都乘以9(2x+1),得9(x﹣3)=2x+1,
解得:x=4,
检验:当x=4时,9(2x+1)≠0,所以x=4是原方程的解,
即原方程的解是x=4;
(2)原方程化为:+=﹣1,
方程两边都乘以(x+2)(x﹣2),得﹣(x+2)2+15=﹣(x+2)(x﹣2),
解得:x=,
检验:当x=时,(x+2)(x﹣2)≠0,所以x=是原方程的解,
即原方程的解是x=.
21.解:(1),
去分母得,3(x﹣2)=2(x+2),
去括号得,3x﹣6=2x+4,
移项得,x=10,
经检验:x=10为方程的解,
∴方程的解为x=10;
(2),
去分母得,(x﹣2)2﹣(x+2)2=16,
去括号得,﹣8x=16,
两边同时除以﹣8得,x=﹣2,
经检验:x=﹣2为方程的增根,
∴原方程无解.
22.解:(1)﹣=0,
去分母得,3x﹣2(x﹣1)=0,
去括号得,x=﹣2,
经检验:x=﹣2是方程的根,
∴x=﹣2是原方程的解;
(2)=﹣3,
去分母得,1=﹣(1﹣x)﹣3(x﹣2),
去括号得,1=﹣1+x﹣3x+6,
解得:x=2,
检验:x=2是增根,
∴原方程无解.
23.解:(1)去分母得:8(2x﹣1)=9(x+2),
去括号得:16x﹣8=9x+18,
化简得:7x=26,
∴x=,
检验:当x=时,(x+2)(2x﹣1)≠0,
∴原方程的解为x=;
(2)去分母得:(x﹣1)2﹣(x+1)2=4,
去括号得:x2﹣2x+1﹣x2﹣2x﹣1=4,
化简得:﹣4x=4,
∴x=﹣1,
检验:当x=﹣1时,(x+1)(x﹣1)=0,
∴x=﹣1是增根,原方程无解.
24.解:(1)整理,得:,
去分母,得:﹣2x﹣(x﹣3)=4,
解得:x=﹣,
经检验:当x=﹣时,x﹣3≠0,
∴x=﹣是原分式方程的解,
(2)整理,得:,
,
去分母,得:2(x+4)=4(x+2),
解得:x=0,
经检验:当x=0时,(x+4)(x﹣4)≠0,x(x+2)=0,
∴x=0是原方程的增根,
原分式方程无解.
25.(1)解:方程两边同时乘以(x+2)(x﹣2),得,
x+2=3,
解得x=1,
经检验,x=1是原方程的解,
∴原方程的解为x=1.
(2)解:方程两边同时乘以(y﹣3)得,
2﹣y=﹣1﹣2(y﹣3),
解得y=3,
当y=3时,y﹣3=0,
∴原方程无解
26.解:(1)去分母得:2﹣x=3(x﹣3),
去括号得:2﹣x=3x﹣9,
解得:x=,
检验:当x=时,(x﹣3)(2﹣x)≠0,
∴分式方程的解为x=;
(2)去分母得:3x(x﹣2)﹣2(x+2)=3(x+2)(x﹣2),
整理得:3x2﹣6x﹣2x﹣4=3x2﹣12,
移项合并得:﹣8x=﹣8,
解得:x=1,
检验:当x=1时,(x+2)(x﹣2)≠0,
∴分式方程的解为x=1.
27.解:(1)方程两边同时乘以x﹣2得x﹣3+x﹣2=3,
解整式方程得,x=4,
检验:当x=4时,x﹣2≠0
∴x=4是原方程的解.
(2)方程两边同时乘以(x﹣1)(2x+3)得:2x2﹣x﹣6=2(x﹣2)(x﹣1),
整理得:5x=10,
解得:x=2,
检验:当x=2时,(x﹣1)(2x+3)≠0,
∴分式方程的解为x=2.
28.解:(1)去分母得:2x=5(x+3),
解得:x=﹣5
检验:x=﹣5时,x(x+3)≠0,
∴x=﹣5是原方程的解;
(2)去分母得:8+x2﹣4=x (x+2),
解得:x=2,
检验:当x=2时,(x+2)(x﹣2)=0,
∴x=2 是增根,原方程无解.
29.解:(1)去分母得:2x=3x﹣9,
解得:x=9,
检验:当x=9时,x(x﹣3)≠0,
∴分式方程的解为x=9;
(2)去分母得:4=(x+2)(x+1)﹣(x2﹣1),
去括号得:4=(x+2)(x+1)﹣x2+1,
整理得:4=x2+3x+2﹣x2+1,
解得:x=,
检验:当x=时,(x+1)(x﹣1)≠0,
∴分式方程的解为x=.
30.解:(1)由题意可得:第一步变化过程的依据是:分式的基本性质,
故答案为:分式的基本性质;
(2)方程两边同乘(x﹣3)得:x﹣2﹣2(x﹣3)=10﹣3x,
去括号,得:x﹣2﹣2x+6=10﹣3x,
移项,得:x﹣2x+3x=10﹣6+2,
合并同类项,得:2x=6,
系数化1,得:x=3,
检验:当x=3时,x﹣3=0,
∴x=3是原方程的增根,
∴原分式方程无解.
