2021-2022学年九年级上册数学人教版24.1.4圆周角1 同步作业(word版含答案)
文档属性
| 名称 | 2021-2022学年九年级上册数学人教版24.1.4圆周角1 同步作业(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 183.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-31 16:41:21 | ||
图片预览


文档简介
24.14圆周角同步作业(1)
选择题
如图,线段AB是⊙O的直径,弦CD⊥AB,∠CAB=200,则∠AOD等于( )
A 1200 B. 1400 C. 1500 D. 1600
如图,在Rt△ABC中,∠ACB=900,AC=6,BC=8,若以AC为直径的⊙O交AB于点D,则CD的长为( )
B. C. D. 5
如图,BC是⊙O的直径,AB是⊙O的弦,若∠AOC=600,则∠OAB的度数是( )
200 B. 250 C. 300 D. 350
如图,A、B是⊙O上的两点,∠AOB=600,OF⊥AB交⊙O于点F,则∠BAF等于( )
200 B. 22.50 C. 150 D. 12.50
如图,⊙O的半径OB为4,OC⊥AB于点D,∠BAC=300,则OD的长是( )
B. C. 2 D. 3
如图,AB为⊙O的直径,C, D为⊙O上的两点,若∠ABD=540,则∠C的度数为()
340 B. 360 C. 460 D. 540
如图,点A,B,C为⊙O上的三点,∠AOB=,∠BAC=300,则∠AOC的度数为( )
A.1000 B. 900 C. 800 D.600
如图,A, B, C是⊙O上的三点,若∠O=700,则∠C的度数是( )
400 B. 350 C. 300 D. 250
如图,AB是⊙O的弦,且AB=6,点C是弧AB中点,点D是优弧AB上的一点,∠ADC=300,则圆心O到弦AB的距离等于( )
B. C . D.
如图,在以AB为直径的⊙O中,点C为圆上的一点,弧BC=3弧AC,弦CD⊥AB于点E,弦AF交弦BC于点G,若点H是AG的中点,则∠CBF的度数为( )
180 B. 210 C. 22.50 D.300
填空题
如图,△ABC内接于⊙O,∠BAC=1200,AB=AC,BD是⊙O的直径,若AD=3,则BC的长为______.
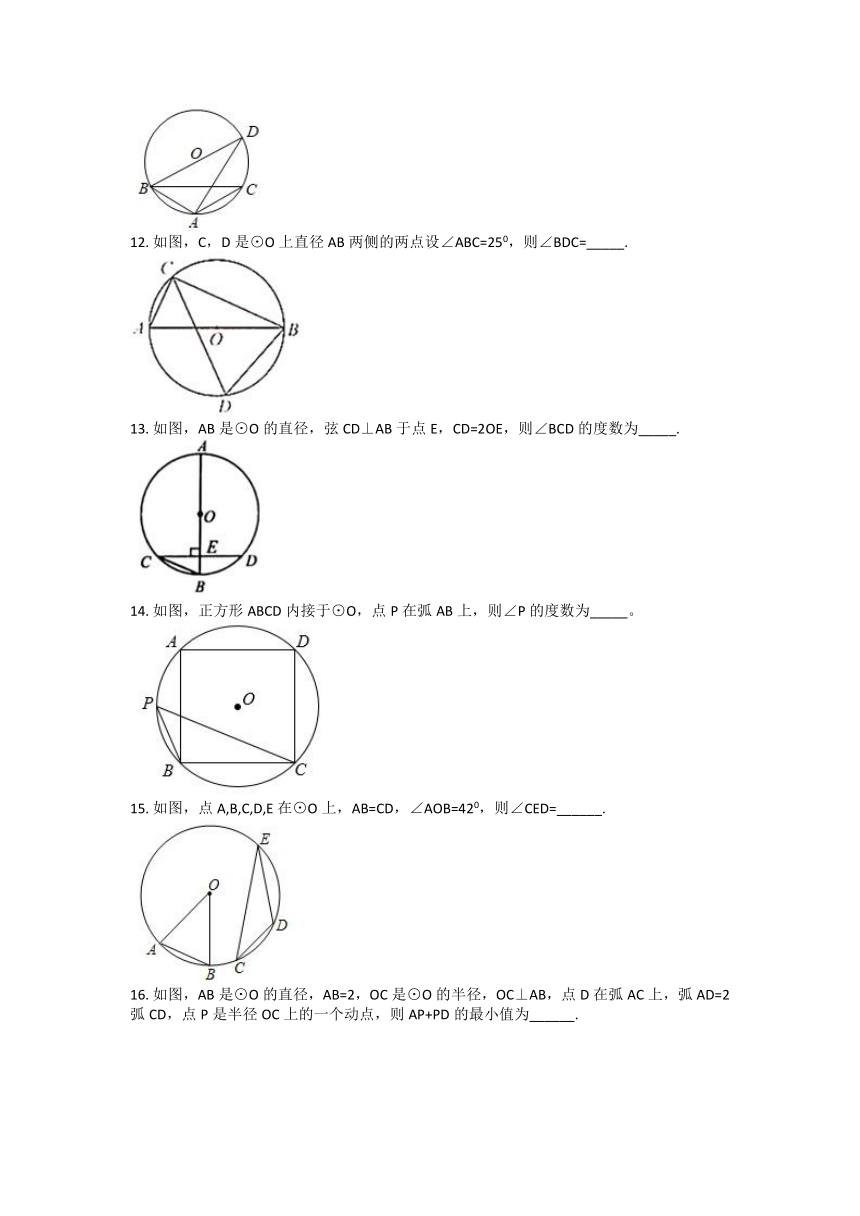
如图,C,D是⊙O上直径AB两侧的两点设∠ABC=250,则∠BDC=_____.
如图,AB是⊙O的直径,弦CD⊥AB于点E,CD=2OE,则∠BCD的度数为_____.
如图,正方形ABCD内接于⊙O,点P在弧AB上,则∠P的度数为_____。
如图,点A,B,C,D,E在⊙O上,AB=CD,∠AOB=420,则∠CED=______.
如图,AB是⊙O的直径,AB=2,OC是⊙O的半径,OC⊥AB,点D在弧AC上,弧AD=2弧CD,点P是半径OC上的一个动点,则AP+PD的最小值为______.
如图,AB是⊙O的直径,AB=8,点M在⊙O上,∠MAB=200,N是弧MB的中点,P是直径AB上的一动点,若MN=1,则△PMN的周长的最小值为____
已知⊙O的半径是7,AB是⊙O的弦,且AB的长为7,则弦AB所对的圆周角的度数 为_____。
一块直角三角板的300的角的顶点A落在⊙O上,两边分别交⊙O于B,C两点,若弦BC=2,则⊙O的半径 为_____
解答题
20.已知如图,△ABC内接于⊙O,∠CAB=300,∠CBA=450,CD⊥AB于点D,若⊙O的半径为4,求弦AB的长。
21.如图,AB是⊙O直径,CD是⊙O的弦,∠ADC=260,求∠CAB的度数。
22.如图,在△ABC中,AC=BC,D是AB上一点,⊙O经过点A,C,D,过点D作DE∥BC,交⊙O于点E,连接CE。求证:四边形DBCE是平行四边形
23.如图,⊙O的直径AB为10cm,弦BC=8cm,∠ACB的平分线交⊙O于点D。连接AD,BD,求四边形ABCD的面积。
参考答案
选择题
B 2.C 3.C 4.C 5.C 6.B 7.C 8.B 9.C 10.C
填空题
3
650
13. 22.50
14. 450
15. 210
16.
17. 5
18. 600或1200
19. 2
三、解答题
20.解:连接OC,OB,则∠O=2∠A
∵OB=OC
∴△BOC是等边三角形
∵⊙O的半径为4
∴BC=4
∵CD⊥AB,∠CBA=450
∴BD=CD=
∵∠A=300,
∴AC=4
∴AD=
∴AB=AD+DB=+
21.解:连接BC
∵AB是⊙O的直径
∴∠ACB=900
∵弧AC=弧AC
∴∠CBA=∠ADC=260
∴∠CAB=1800-∠ACB-∠CBA=1800-900-260=640
即 ∠CAB=640
22.证明:∵AC=BC,∴∠BAC=∠B
∵DE∥BC,
∴∠ADE=∠B
∴∠ADE=∠BAC
又在⊙O中,∠BAC=∠CED
∴∠ADE=∠CED
∴BD∥CE
又∵DF∥BC
∴四边形DBCE是平行四边形
23.解:∵AB为直径,
∴∠ADB=900
又∵CD平分∠ACB,即 ∠ACD=∠BCD
∴弧AD=弧BD
∴AD=BD
∵直角△ABD中,AD=BD,
则AD=BD=
则
在直角△ABC中,AC=
则
则
选择题
如图,线段AB是⊙O的直径,弦CD⊥AB,∠CAB=200,则∠AOD等于( )
A 1200 B. 1400 C. 1500 D. 1600
如图,在Rt△ABC中,∠ACB=900,AC=6,BC=8,若以AC为直径的⊙O交AB于点D,则CD的长为( )
B. C. D. 5
如图,BC是⊙O的直径,AB是⊙O的弦,若∠AOC=600,则∠OAB的度数是( )
200 B. 250 C. 300 D. 350
如图,A、B是⊙O上的两点,∠AOB=600,OF⊥AB交⊙O于点F,则∠BAF等于( )
200 B. 22.50 C. 150 D. 12.50
如图,⊙O的半径OB为4,OC⊥AB于点D,∠BAC=300,则OD的长是( )
B. C. 2 D. 3
如图,AB为⊙O的直径,C, D为⊙O上的两点,若∠ABD=540,则∠C的度数为()
340 B. 360 C. 460 D. 540
如图,点A,B,C为⊙O上的三点,∠AOB=,∠BAC=300,则∠AOC的度数为( )
A.1000 B. 900 C. 800 D.600
如图,A, B, C是⊙O上的三点,若∠O=700,则∠C的度数是( )
400 B. 350 C. 300 D. 250
如图,AB是⊙O的弦,且AB=6,点C是弧AB中点,点D是优弧AB上的一点,∠ADC=300,则圆心O到弦AB的距离等于( )
B. C . D.
如图,在以AB为直径的⊙O中,点C为圆上的一点,弧BC=3弧AC,弦CD⊥AB于点E,弦AF交弦BC于点G,若点H是AG的中点,则∠CBF的度数为( )
180 B. 210 C. 22.50 D.300
填空题
如图,△ABC内接于⊙O,∠BAC=1200,AB=AC,BD是⊙O的直径,若AD=3,则BC的长为______.
如图,C,D是⊙O上直径AB两侧的两点设∠ABC=250,则∠BDC=_____.
如图,AB是⊙O的直径,弦CD⊥AB于点E,CD=2OE,则∠BCD的度数为_____.
如图,正方形ABCD内接于⊙O,点P在弧AB上,则∠P的度数为_____。
如图,点A,B,C,D,E在⊙O上,AB=CD,∠AOB=420,则∠CED=______.
如图,AB是⊙O的直径,AB=2,OC是⊙O的半径,OC⊥AB,点D在弧AC上,弧AD=2弧CD,点P是半径OC上的一个动点,则AP+PD的最小值为______.
如图,AB是⊙O的直径,AB=8,点M在⊙O上,∠MAB=200,N是弧MB的中点,P是直径AB上的一动点,若MN=1,则△PMN的周长的最小值为____
已知⊙O的半径是7,AB是⊙O的弦,且AB的长为7,则弦AB所对的圆周角的度数 为_____。
一块直角三角板的300的角的顶点A落在⊙O上,两边分别交⊙O于B,C两点,若弦BC=2,则⊙O的半径 为_____
解答题
20.已知如图,△ABC内接于⊙O,∠CAB=300,∠CBA=450,CD⊥AB于点D,若⊙O的半径为4,求弦AB的长。
21.如图,AB是⊙O直径,CD是⊙O的弦,∠ADC=260,求∠CAB的度数。
22.如图,在△ABC中,AC=BC,D是AB上一点,⊙O经过点A,C,D,过点D作DE∥BC,交⊙O于点E,连接CE。求证:四边形DBCE是平行四边形
23.如图,⊙O的直径AB为10cm,弦BC=8cm,∠ACB的平分线交⊙O于点D。连接AD,BD,求四边形ABCD的面积。
参考答案
选择题
B 2.C 3.C 4.C 5.C 6.B 7.C 8.B 9.C 10.C
填空题
3
650
13. 22.50
14. 450
15. 210
16.
17. 5
18. 600或1200
19. 2
三、解答题
20.解:连接OC,OB,则∠O=2∠A
∵OB=OC
∴△BOC是等边三角形
∵⊙O的半径为4
∴BC=4
∵CD⊥AB,∠CBA=450
∴BD=CD=
∵∠A=300,
∴AC=4
∴AD=
∴AB=AD+DB=+
21.解:连接BC
∵AB是⊙O的直径
∴∠ACB=900
∵弧AC=弧AC
∴∠CBA=∠ADC=260
∴∠CAB=1800-∠ACB-∠CBA=1800-900-260=640
即 ∠CAB=640
22.证明:∵AC=BC,∴∠BAC=∠B
∵DE∥BC,
∴∠ADE=∠B
∴∠ADE=∠BAC
又在⊙O中,∠BAC=∠CED
∴∠ADE=∠CED
∴BD∥CE
又∵DF∥BC
∴四边形DBCE是平行四边形
23.解:∵AB为直径,
∴∠ADB=900
又∵CD平分∠ACB,即 ∠ACD=∠BCD
∴弧AD=弧BD
∴AD=BD
∵直角△ABD中,AD=BD,
则AD=BD=
则
在直角△ABC中,AC=
则
则
同课章节目录
