2021-2022学年人教版 九年级数学上册24.1.2 垂直于弦的直径 课后练习(word版含解析)
文档属性
| 名称 | 2021-2022学年人教版 九年级数学上册24.1.2 垂直于弦的直径 课后练习(word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 645.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-31 16:43:45 | ||
图片预览



文档简介
24.1.2 垂直于弦的直径
一、单选题
1.已知的半径为5,一条弦的弦心距为3,则此弦的长为( )
A.6 B.4 C.8 D.10
2.如图,已知⊙O的半径为5,弦AB的长为8,P是AB的延长线上一点,BP=2,则OP等于( )
A. B. C. D.
3.下列命题中不正确的是( )
A.圆是轴对称图形,任何一条直径所在直线都是圆的对称轴
B.圆是中心对称图形,圆心是它的对称中心
C.图形经过旋转所得的对应点到旋转中心的距离相等
D.平分弦的直径一定垂直于这条弦
4.如图,为的直径,弦,垂足为,,,则的半径为( )
A.3 B.4 C.5 D.无法确定
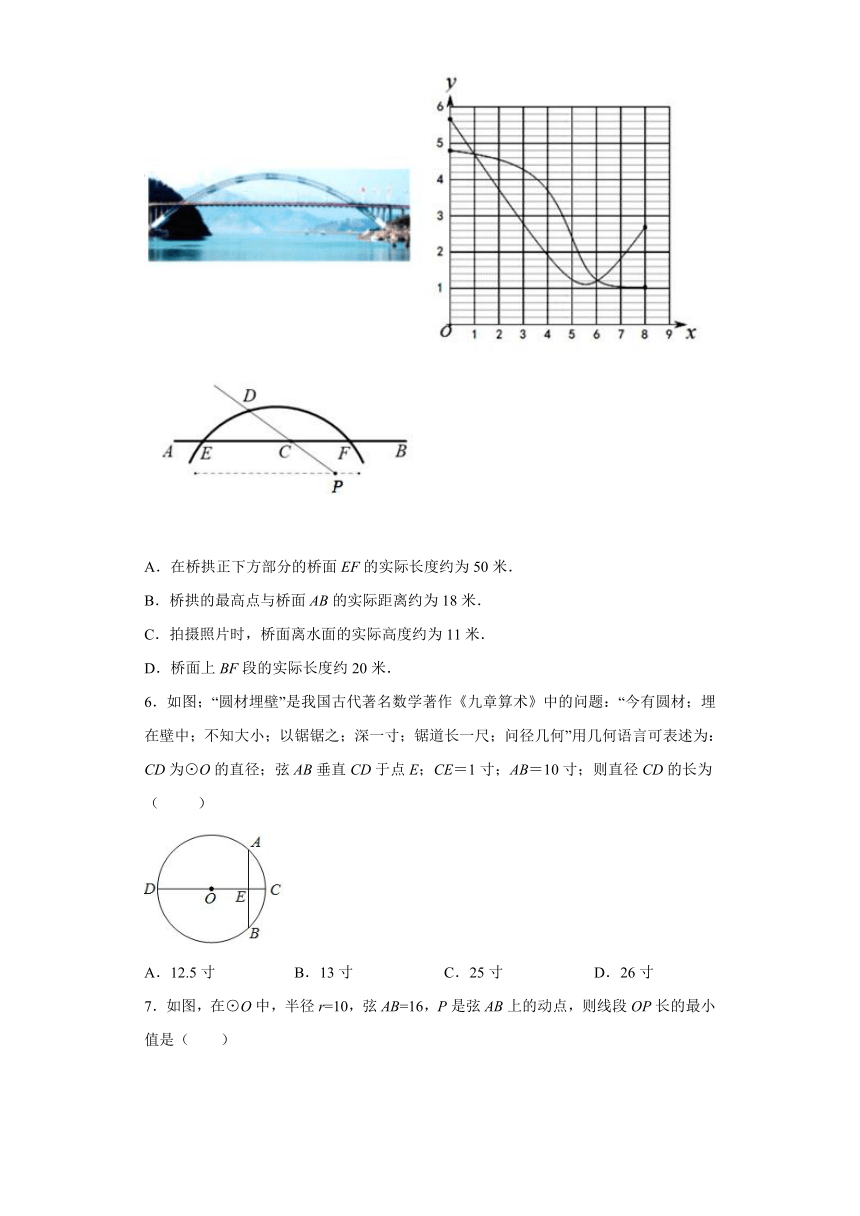
5.如图,这是一张从某大桥正侧面拍摄的照片,大桥的主桥拱为圆弧型,桥面AB长为80米,且与水面平行,小王用计算机根据照片对大桥进行了模拟分析,在桥正下方的水面上取一点P,在桥面AB上取点C,作射线PC交弧(主桥拱)于点D,画出了PC与PD关于AC长的函数图象,下列对此桥的判断不合理的是( )
A.在桥拱正下方部分的桥面EF的实际长度约为50米.
B.桥拱的最高点与桥面AB的实际距离约为18米.
C.拍摄照片时,桥面离水面的实际高度约为11米.
D.桥面上BF段的实际长度约20米.
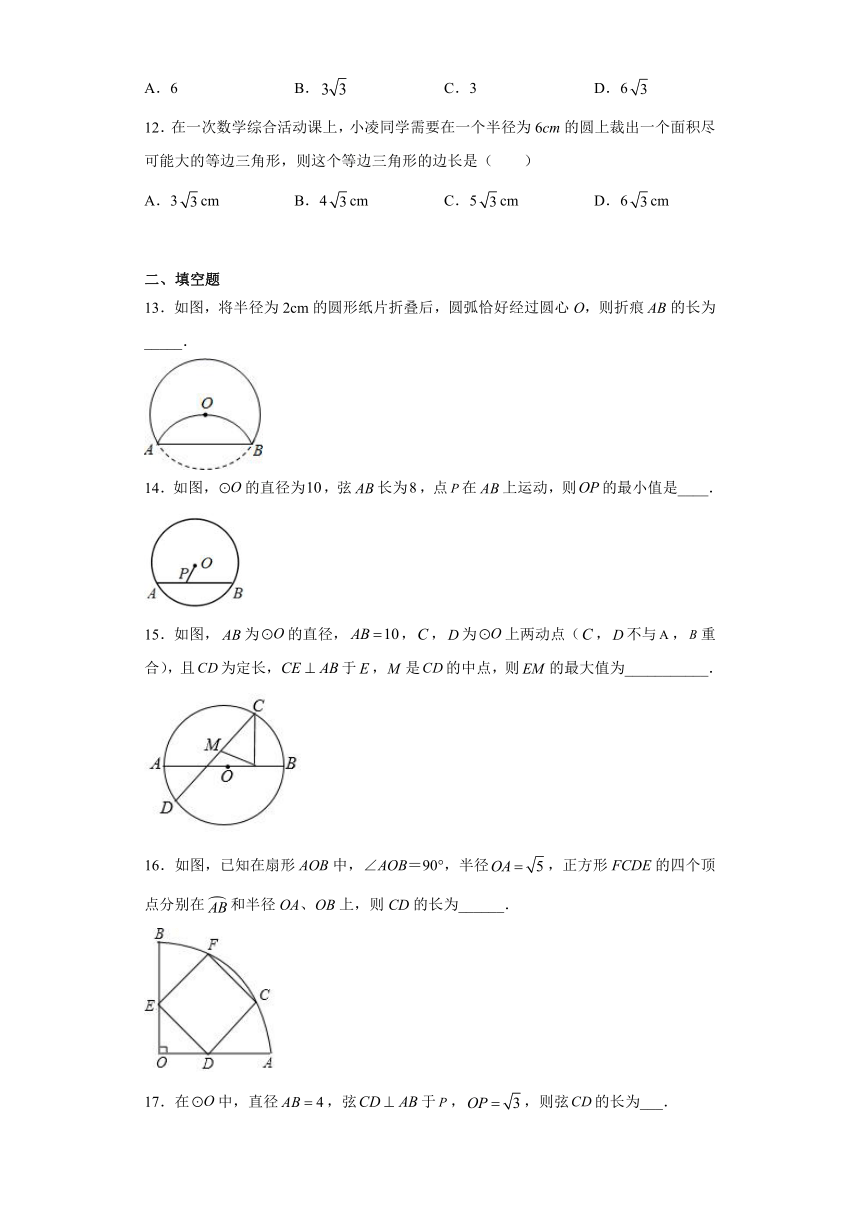
6.如图;“圆材埋壁”是我国古代著名数学著作《九章算术》中的问题:“今有圆材;埋在壁中;不知大小;以锯锯之;深一寸;锯道长一尺;问径几何”用几何语言可表述为:CD为⊙O的直径;弦AB垂直CD于点E;CE=1寸;AB=10寸;则直径CD的长为( )
A.12.5寸 B.13寸 C.25寸 D.26寸
7.如图,在⊙O中,半径r=10,弦AB=16,P是弦AB上的动点,则线段OP长的最小值是( )
A.10 B.16 C.6 D.8
8.如图,是的直径,弦于点,连接、,下列结论中不一定正确的是( )
A. B. C. D.
9.下列说法正确的是( )
A.垂直于弦的直线平分弦所对的两条弧 B.平分弦的直径垂直于弦
C.垂直于直径的弦平分这条直径 D.弦的垂直平分线经过圆心
10.如图,是的直径,弦于点,,,则的长为( )
A.4 B.5 C.8 D.16
11.如图,是的直径,弦于点E,,的半径为6,则弦的长为( )
A.6 B. C.3 D.6
12.在一次数学综合活动课上,小凌同学需要在一个半径为6cm的圆上裁出一个面积尽可能大的等边三角形,则这个等边三角形的边长是( )
A.3cm B.4cm C.5cm D.6cm
二、填空题
13.如图,将半径为2cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长为_____.
14.如图,的直径为,弦长为,点在上运动,则的最小值是____.
15.如图,为的直径,,,为上两动点(,不与,重合),且为定长,于,是的中点,则的最大值为___________.
16.如图,已知在扇形AOB中,∠AOB=90°,半径,正方形FCDE的四个顶点分别在和半径OA、OB上,则CD的长为______.
17.在中,直径,弦于,,则弦的长为___.
18.如图,在半径为的中,,弦于点,则等于______.
19.如图,的半径为6,弦垂直平分,则________,________.
三、解答题
20.如图,已知为的弦,且,求证:是等腰三角形.
21.如图,在单位长度为的正方形网格中,一段圆弧经过网格的交点、、.请完成如下操作:
(1)以点为原点、网格边长为单位长,建立平面直角坐标系;
(2)仅用一把无刻度直尺,利用网格,标出圆弧所在圆的圆心,则点的坐标为______.(不写作法,保留作图痕迹)
(3)直接写出的半径______.
22.阅读理解:小明热爱数学,在课外书上看到了一个有趣的定理--“中线长定理”:三角形两边的平方和等于第三边的一半与第三边上的中线的平方和的两倍.如图1,在△ABC中,点D为BC的中点,根据“中线长定理”,可得:
AB2+AC2=2AD2+2BD2.小明尝试对它进行证明,部分过程如下:
解:过点A作AE⊥BC于点E,如图2,在Rt△ABE中,AB2=AE2+BE2,
同理可得:AC2=AE2+CE2,AD2=AE2+DE2,
为证明的方便,不妨设BD=CD=x,DE=y,
∴AB2+AC2=AE2+BE2+AE2+CE2=…
(1)请你完成小明剩余的证明过程;
理解运用:
(2)①在△ABC中,点D为BC的中点,AB=6,AC=4,BC=8,则AD= ;
②如图3,⊙O的半径为6,点A在圆内,且OA=2,点B和点C在⊙O上,且∠BAC=90°,点E、F分别为AO、BC的中点,则EF的长为 ;
拓展延伸:
(3)小明解决上述问题后,联想到如下的题目:
如图4,已知⊙O的半径为5,以A(-3,4)为直角顶点的△ABC的另两个顶点B,C都在⊙O上,D为BC的中点,求AD长的最大值.
请你利用上面的方法和结论,求出AD长的最大值.
参考答案
1.C
解:根据垂径定理,由已知得,这条弦的一半为=4,
所以弦为8.
故选:C.
2.D
解:过O作OC⊥AB于C,
则∠OCP=∠ACO=90°,
∵OC⊥AB,OC过O,
∴AC=BC=AB=×8=4,
∵BP=2,
∴PC=BC+BP=6,
在Rt△ACO中,由勾股定理得:OC= ,
在Rt△PCO中,由勾股定理得:OP= ,
故选:D.
3.D
解:、圆是轴对称图形,任何一条直径所在直线都是圆的对称轴,正确,不符合题意;
、圆是中心对称图形,圆心是它的对称中心,正确,不符合题意;
、同弧或等弧所对的圆心角相等,正确,不符合题意;
、平分弦(不是直径)的直径一定垂直于这条弦,错误,符合题意,
故选:D.
4.C
连接OA,
∵为的直径,弦,
∴AE=AB=3,
设OA=OC=x,则OE=x-1,
∴,解得:x=5,
∴的半径为5.
故选C.
5.B
解:A、函数图像中PC与PD函数图像的交点即为桥拱与桥面的交点E、F,对应的横坐标分别为1、6,根据横坐标最大为8,AB=80米,
∴横坐标一个单位长度对应的长度是10米,
∴EF=10×(6-1)=50米,故A不符合题意;
B、如图当D在最高点,作DH⊥AB于H,若DH=18m,则斜边CD的长大于18m,即,即在函数图像上,而由函数图像可知,PC与PD的差值最大没有达到1.8,因此桥拱的最高点与桥面AB的实际距离小于18米,故B符合题意;
C、PC的纵坐标最低时,此时PC⊥AB,由函数图像可知,此时正好在1.1处,即高度为11米,故C不符合题意;
D、由函数图像可知F的横坐标为6,B的横坐标为8,即F、B之间的距离为20,故D不符合题意;
故选B.
6.D
解:连接OA,如图所示,
设直径CD的长为2x寸,则半径OA=OC=x寸,
∵CD为⊙O的直径,弦AB⊥CD于E,AB=10寸,
∴AE=BE=AB=×10=5寸,
根据勾股定理得x2=52+(x-1)2,
解得x=13,
CD=2x=2×13=26(寸).
故选:D.
7.C
解:过点O作OC⊥AB于C,连接OA,
∴AC=AB=×16=8,
∵⊙O的半径r=10,
∴OA=10,
在Rt△OAC中,由勾股定理得:OC==6,
由垂线段最短得:当P与C重合时,OP最短=OC=6,
故选:C.
8.C
∵直径垂直于弦于点,则由垂径定理可得,,,,故选项A,B,D正确;无法得出,故C错误.
故选C.
9.D
解:A.垂直于弦的直径平分弦所对的两条弧,所以A选项错误;
B.平分弦(非直径)的直径垂直于弦,所以B选项错误;
C.垂直于直径的弦被这条直径平分,所以C选项错误;
D.弦的垂直平分线经过圆心,所以D选项正确.
故选D.
10.C
解:∵AB是⊙O的直径,弦CD⊥AB,
∴CM=DM,
∵AM=2,BM=8,
∴AB=10,
∴OA=OC=5,
在Rt△OCM中,OM2+CM2=OC2,
∴CM==4,
∴CD=8.
故选:C.
11.D
连接,如图,
是的直径,弦
又
为等边三角形,
故选D
12.D
解:依题意得,
连接,,作于点,
∵,
∴,,
∴
∴
由勾股定理可得
故选:D.
13.
如图所示,过点作于,连接,
,,,
在中,由勾股定理得:,
由垂径定理得:.
故答案为:.
14.3
解:当OP⊥AB时,OP的值最小,
则AP′=BP′=AB=4,
如图所示,连接OA,
在Rt△OAP′中,AP′=4,OA=5,
则根据勾股定理知OP′=3,即OP的最小值为3.
15.5
解:如图,当CD∥AB时,EM的值最大,
连接OM、CE、OC,
∵DM=CM,
∴OM⊥CD,
∵CD∥AB,CE⊥AB,
∴∠OMC=∠MOB=∠OEC=90°,
∴四边形OMCE是矩形,
∴EM=OC=5,
∴EM的最大值为5,
故答案为:5.
16.
解:过点O作OH⊥CF于点H,交DE于点K,连接OC,
∵OH过圆心,OH⊥CF
∴CH=HF,
∵四边形FCDE是正方形,
∴OH⊥DE,DK=EK,
∴△OED是等腰直角三角形,OK=EK=DK,
设CD=x,则HK=x,HC=OK=DK=,
在Rt△OHC中,OC2=OH2+HC2,
∴5=(x+)2+
∴x=
∴CD的长为
故答案为:.
17.2
解:连接,
在中,直径,
,
∵弦于,,
,
.
故答案为:2.
18.6
解:连接OA,如图,
∵OC⊥AB,
∴AC=BC=AB=8,
在Rt△OAC中,OC===6(cm).
故答案为6.
19.
连接,设交于点,则垂直平分,
弦垂直平分,
四边形是菱形,
,,
,
是等边三角形,
,
,
,
,
,
,
故答案为:.
20.见解析
证明:从O向AB引垂线,交点为E,
则根据垂径定理可知AE=BE
∵AC=BD,
∴CE=DE.
∴OE是CD的垂直平分线.
所以OC=OD.
∴△OCD为等腰三角形.
21.(1)见解析;(2)作图见解析,;(3)
解:(1)以为原点,水平方向为轴,竖直方向为轴建立平面直角坐标系,如下图:
(2)连接、,找出相应的格点,作出线段、的垂直平分线,交点即是圆心,如下图:
由图形可得点坐标为
(3)连接,如下图:
由图形可得点坐标为,即
由(2)得
由勾股定理得:
即半径长为
22.(1)见解析;(2)①;②4;(3)AD长的最大值为10.
解:(1)过点A作AE⊥BC于点E,如图2,
在Rt△ABE中,AB2=AE2+BE2,
同理可得:AC2=AE2+CE2,AD2=AE2+DE2,
为证明的方便,不妨设BD=CD=x,DE=y,
∴AB2+AC2=2AE2+(x+y)2+(x-y)2=2AE2+2x2+2y2
=2AE2+2BD2+2DE2
=2AD2+2BD2;
(2)①∵AB2+AC2=2AD2+2BD2,
∴62+42=2AD2+2×42,
∴AD=;
②如图3中,
∵AF是△ABC的中线,EF是△AEO的中线,OF是△BOC的中线,
∵2EF2+2AE2=AF2+OF2,
2AF2+2BF2=AB2+AC2,
OF2=OB2-BF2,
∴4EF2=2OB2-4AE2=2OB2-OA2,
∴EF2=OB2-OA2=16,
∴EF=4(负根舍弃),
故答案为:①;②4;
(3)如图4中,连接OA,取OA的中点E,连接DE.
由(2)的②可知:DE2=OB2-OA2=,
∴DE=;
在△ADE中,AE=,DE=,
∵AD≤AE+DE,
∴AD长的最大值为+=10.
一、单选题
1.已知的半径为5,一条弦的弦心距为3,则此弦的长为( )
A.6 B.4 C.8 D.10
2.如图,已知⊙O的半径为5,弦AB的长为8,P是AB的延长线上一点,BP=2,则OP等于( )
A. B. C. D.
3.下列命题中不正确的是( )
A.圆是轴对称图形,任何一条直径所在直线都是圆的对称轴
B.圆是中心对称图形,圆心是它的对称中心
C.图形经过旋转所得的对应点到旋转中心的距离相等
D.平分弦的直径一定垂直于这条弦
4.如图,为的直径,弦,垂足为,,,则的半径为( )
A.3 B.4 C.5 D.无法确定
5.如图,这是一张从某大桥正侧面拍摄的照片,大桥的主桥拱为圆弧型,桥面AB长为80米,且与水面平行,小王用计算机根据照片对大桥进行了模拟分析,在桥正下方的水面上取一点P,在桥面AB上取点C,作射线PC交弧(主桥拱)于点D,画出了PC与PD关于AC长的函数图象,下列对此桥的判断不合理的是( )
A.在桥拱正下方部分的桥面EF的实际长度约为50米.
B.桥拱的最高点与桥面AB的实际距离约为18米.
C.拍摄照片时,桥面离水面的实际高度约为11米.
D.桥面上BF段的实际长度约20米.
6.如图;“圆材埋壁”是我国古代著名数学著作《九章算术》中的问题:“今有圆材;埋在壁中;不知大小;以锯锯之;深一寸;锯道长一尺;问径几何”用几何语言可表述为:CD为⊙O的直径;弦AB垂直CD于点E;CE=1寸;AB=10寸;则直径CD的长为( )
A.12.5寸 B.13寸 C.25寸 D.26寸
7.如图,在⊙O中,半径r=10,弦AB=16,P是弦AB上的动点,则线段OP长的最小值是( )
A.10 B.16 C.6 D.8
8.如图,是的直径,弦于点,连接、,下列结论中不一定正确的是( )
A. B. C. D.
9.下列说法正确的是( )
A.垂直于弦的直线平分弦所对的两条弧 B.平分弦的直径垂直于弦
C.垂直于直径的弦平分这条直径 D.弦的垂直平分线经过圆心
10.如图,是的直径,弦于点,,,则的长为( )
A.4 B.5 C.8 D.16
11.如图,是的直径,弦于点E,,的半径为6,则弦的长为( )
A.6 B. C.3 D.6
12.在一次数学综合活动课上,小凌同学需要在一个半径为6cm的圆上裁出一个面积尽可能大的等边三角形,则这个等边三角形的边长是( )
A.3cm B.4cm C.5cm D.6cm
二、填空题
13.如图,将半径为2cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长为_____.
14.如图,的直径为,弦长为,点在上运动,则的最小值是____.
15.如图,为的直径,,,为上两动点(,不与,重合),且为定长,于,是的中点,则的最大值为___________.
16.如图,已知在扇形AOB中,∠AOB=90°,半径,正方形FCDE的四个顶点分别在和半径OA、OB上,则CD的长为______.
17.在中,直径,弦于,,则弦的长为___.
18.如图,在半径为的中,,弦于点,则等于______.
19.如图,的半径为6,弦垂直平分,则________,________.
三、解答题
20.如图,已知为的弦,且,求证:是等腰三角形.
21.如图,在单位长度为的正方形网格中,一段圆弧经过网格的交点、、.请完成如下操作:
(1)以点为原点、网格边长为单位长,建立平面直角坐标系;
(2)仅用一把无刻度直尺,利用网格,标出圆弧所在圆的圆心,则点的坐标为______.(不写作法,保留作图痕迹)
(3)直接写出的半径______.
22.阅读理解:小明热爱数学,在课外书上看到了一个有趣的定理--“中线长定理”:三角形两边的平方和等于第三边的一半与第三边上的中线的平方和的两倍.如图1,在△ABC中,点D为BC的中点,根据“中线长定理”,可得:
AB2+AC2=2AD2+2BD2.小明尝试对它进行证明,部分过程如下:
解:过点A作AE⊥BC于点E,如图2,在Rt△ABE中,AB2=AE2+BE2,
同理可得:AC2=AE2+CE2,AD2=AE2+DE2,
为证明的方便,不妨设BD=CD=x,DE=y,
∴AB2+AC2=AE2+BE2+AE2+CE2=…
(1)请你完成小明剩余的证明过程;
理解运用:
(2)①在△ABC中,点D为BC的中点,AB=6,AC=4,BC=8,则AD= ;
②如图3,⊙O的半径为6,点A在圆内,且OA=2,点B和点C在⊙O上,且∠BAC=90°,点E、F分别为AO、BC的中点,则EF的长为 ;
拓展延伸:
(3)小明解决上述问题后,联想到如下的题目:
如图4,已知⊙O的半径为5,以A(-3,4)为直角顶点的△ABC的另两个顶点B,C都在⊙O上,D为BC的中点,求AD长的最大值.
请你利用上面的方法和结论,求出AD长的最大值.
参考答案
1.C
解:根据垂径定理,由已知得,这条弦的一半为=4,
所以弦为8.
故选:C.
2.D
解:过O作OC⊥AB于C,
则∠OCP=∠ACO=90°,
∵OC⊥AB,OC过O,
∴AC=BC=AB=×8=4,
∵BP=2,
∴PC=BC+BP=6,
在Rt△ACO中,由勾股定理得:OC= ,
在Rt△PCO中,由勾股定理得:OP= ,
故选:D.
3.D
解:、圆是轴对称图形,任何一条直径所在直线都是圆的对称轴,正确,不符合题意;
、圆是中心对称图形,圆心是它的对称中心,正确,不符合题意;
、同弧或等弧所对的圆心角相等,正确,不符合题意;
、平分弦(不是直径)的直径一定垂直于这条弦,错误,符合题意,
故选:D.
4.C
连接OA,
∵为的直径,弦,
∴AE=AB=3,
设OA=OC=x,则OE=x-1,
∴,解得:x=5,
∴的半径为5.
故选C.
5.B
解:A、函数图像中PC与PD函数图像的交点即为桥拱与桥面的交点E、F,对应的横坐标分别为1、6,根据横坐标最大为8,AB=80米,
∴横坐标一个单位长度对应的长度是10米,
∴EF=10×(6-1)=50米,故A不符合题意;
B、如图当D在最高点,作DH⊥AB于H,若DH=18m,则斜边CD的长大于18m,即,即在函数图像上,而由函数图像可知,PC与PD的差值最大没有达到1.8,因此桥拱的最高点与桥面AB的实际距离小于18米,故B符合题意;
C、PC的纵坐标最低时,此时PC⊥AB,由函数图像可知,此时正好在1.1处,即高度为11米,故C不符合题意;
D、由函数图像可知F的横坐标为6,B的横坐标为8,即F、B之间的距离为20,故D不符合题意;
故选B.
6.D
解:连接OA,如图所示,
设直径CD的长为2x寸,则半径OA=OC=x寸,
∵CD为⊙O的直径,弦AB⊥CD于E,AB=10寸,
∴AE=BE=AB=×10=5寸,
根据勾股定理得x2=52+(x-1)2,
解得x=13,
CD=2x=2×13=26(寸).
故选:D.
7.C
解:过点O作OC⊥AB于C,连接OA,
∴AC=AB=×16=8,
∵⊙O的半径r=10,
∴OA=10,
在Rt△OAC中,由勾股定理得:OC==6,
由垂线段最短得:当P与C重合时,OP最短=OC=6,
故选:C.
8.C
∵直径垂直于弦于点,则由垂径定理可得,,,,故选项A,B,D正确;无法得出,故C错误.
故选C.
9.D
解:A.垂直于弦的直径平分弦所对的两条弧,所以A选项错误;
B.平分弦(非直径)的直径垂直于弦,所以B选项错误;
C.垂直于直径的弦被这条直径平分,所以C选项错误;
D.弦的垂直平分线经过圆心,所以D选项正确.
故选D.
10.C
解:∵AB是⊙O的直径,弦CD⊥AB,
∴CM=DM,
∵AM=2,BM=8,
∴AB=10,
∴OA=OC=5,
在Rt△OCM中,OM2+CM2=OC2,
∴CM==4,
∴CD=8.
故选:C.
11.D
连接,如图,
是的直径,弦
又
为等边三角形,
故选D
12.D
解:依题意得,
连接,,作于点,
∵,
∴,,
∴
∴
由勾股定理可得
故选:D.
13.
如图所示,过点作于,连接,
,,,
在中,由勾股定理得:,
由垂径定理得:.
故答案为:.
14.3
解:当OP⊥AB时,OP的值最小,
则AP′=BP′=AB=4,
如图所示,连接OA,
在Rt△OAP′中,AP′=4,OA=5,
则根据勾股定理知OP′=3,即OP的最小值为3.
15.5
解:如图,当CD∥AB时,EM的值最大,
连接OM、CE、OC,
∵DM=CM,
∴OM⊥CD,
∵CD∥AB,CE⊥AB,
∴∠OMC=∠MOB=∠OEC=90°,
∴四边形OMCE是矩形,
∴EM=OC=5,
∴EM的最大值为5,
故答案为:5.
16.
解:过点O作OH⊥CF于点H,交DE于点K,连接OC,
∵OH过圆心,OH⊥CF
∴CH=HF,
∵四边形FCDE是正方形,
∴OH⊥DE,DK=EK,
∴△OED是等腰直角三角形,OK=EK=DK,
设CD=x,则HK=x,HC=OK=DK=,
在Rt△OHC中,OC2=OH2+HC2,
∴5=(x+)2+
∴x=
∴CD的长为
故答案为:.
17.2
解:连接,
在中,直径,
,
∵弦于,,
,
.
故答案为:2.
18.6
解:连接OA,如图,
∵OC⊥AB,
∴AC=BC=AB=8,
在Rt△OAC中,OC===6(cm).
故答案为6.
19.
连接,设交于点,则垂直平分,
弦垂直平分,
四边形是菱形,
,,
,
是等边三角形,
,
,
,
,
,
,
故答案为:.
20.见解析
证明:从O向AB引垂线,交点为E,
则根据垂径定理可知AE=BE
∵AC=BD,
∴CE=DE.
∴OE是CD的垂直平分线.
所以OC=OD.
∴△OCD为等腰三角形.
21.(1)见解析;(2)作图见解析,;(3)
解:(1)以为原点,水平方向为轴,竖直方向为轴建立平面直角坐标系,如下图:
(2)连接、,找出相应的格点,作出线段、的垂直平分线,交点即是圆心,如下图:
由图形可得点坐标为
(3)连接,如下图:
由图形可得点坐标为,即
由(2)得
由勾股定理得:
即半径长为
22.(1)见解析;(2)①;②4;(3)AD长的最大值为10.
解:(1)过点A作AE⊥BC于点E,如图2,
在Rt△ABE中,AB2=AE2+BE2,
同理可得:AC2=AE2+CE2,AD2=AE2+DE2,
为证明的方便,不妨设BD=CD=x,DE=y,
∴AB2+AC2=2AE2+(x+y)2+(x-y)2=2AE2+2x2+2y2
=2AE2+2BD2+2DE2
=2AD2+2BD2;
(2)①∵AB2+AC2=2AD2+2BD2,
∴62+42=2AD2+2×42,
∴AD=;
②如图3中,
∵AF是△ABC的中线,EF是△AEO的中线,OF是△BOC的中线,
∵2EF2+2AE2=AF2+OF2,
2AF2+2BF2=AB2+AC2,
OF2=OB2-BF2,
∴4EF2=2OB2-4AE2=2OB2-OA2,
∴EF2=OB2-OA2=16,
∴EF=4(负根舍弃),
故答案为:①;②4;
(3)如图4中,连接OA,取OA的中点E,连接DE.
由(2)的②可知:DE2=OB2-OA2=,
∴DE=;
在△ADE中,AE=,DE=,
∵AD≤AE+DE,
∴AD长的最大值为+=10.
同课章节目录
