2021-2022学年冀教版九年级数学上册26.4解直角三角形的应用 题型分类训练(word版含答案)
文档属性
| 名称 | 2021-2022学年冀教版九年级数学上册26.4解直角三角形的应用 题型分类训练(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 497.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-01 07:05:47 | ||
图片预览


文档简介
2021-2022学年冀教版九年级数学上册《26.4解直角三角形的应用》题型分类训练(附答案)
一.解直角三角形的应用
1.根据道路管理规定,在广州某段笔直公路上行驶的车辆,限速40千米/时;已知交警测速点M到该公路A点的距离为10米,∠MAB=45°,∠MBA=37°(如图所示),现有一辆汽车由A往B方向匀速行驶,测得此车从A点行驶到B点所用的时间为2秒.
(1)求测速点M到该公路的距离.
(2)通过计算判断此车是否超速.(数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
二.解直角三角形的应用-坡度坡角问题
2.如图所示,河堤横断面迎水坡AB的坡比是1:,堤高BC=5m,则坡面AB的长是( )
A.10m B.m C.15m D.m
3.江堤的横断面如图,堤高BC=10米,迎水坡AB的坡比是1:,则堤脚AC的长是( )
A.20米 B.20米 C.米 D.10米
4.如图,一小型水库堤坝的横断面为直角梯形,坝顶BC宽6m,坝高14m,斜坡CD的坡度i=1:2,则坝底AD的长为( )
A.13m B.34m C.(6+)m D.40m
5.如图,有一斜坡AB,坡顶B离地面的高度BC为30m,斜坡的倾斜角是∠BAC,若tan∠BAC=,则此斜坡的水平距离AC为( )
A.75m B.50m C.30m D.12m
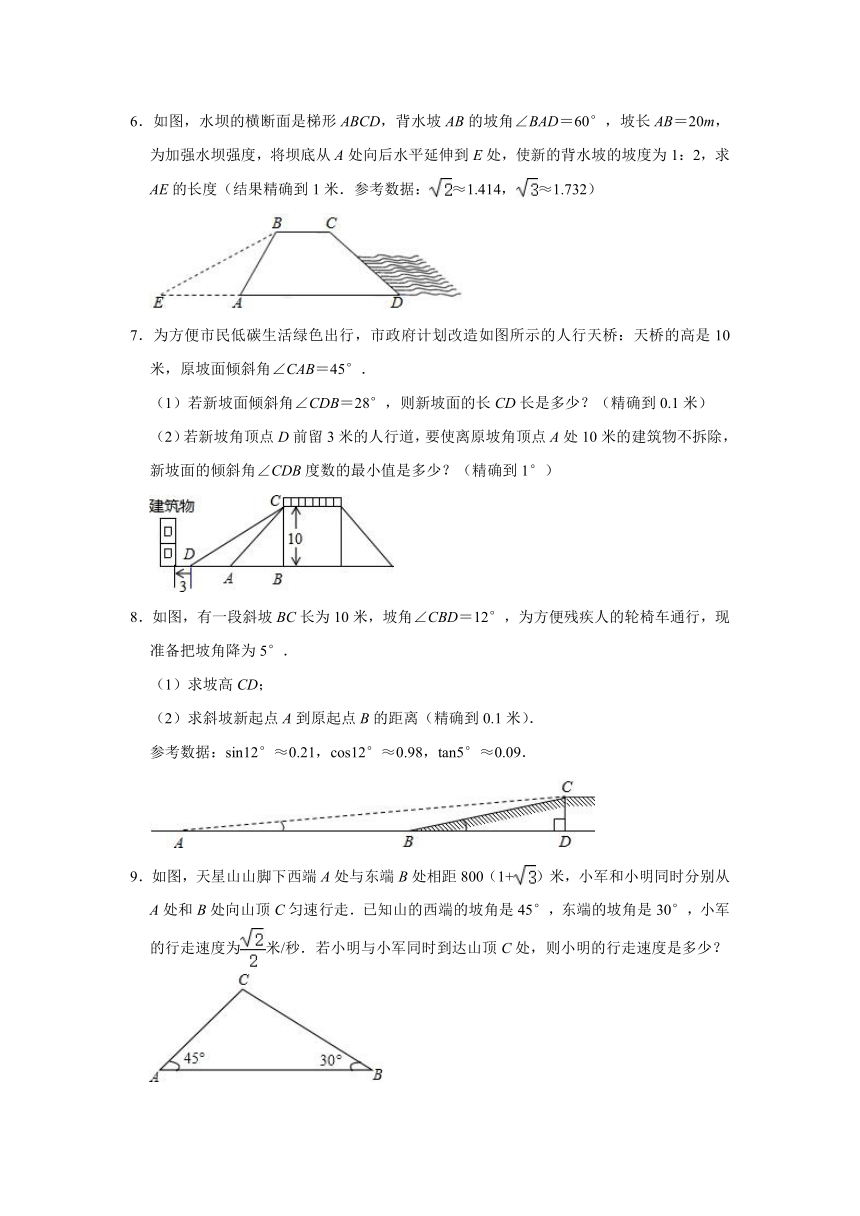
6.如图,水坝的横断面是梯形ABCD,背水坡AB的坡角∠BAD=60°,坡长AB=20m,为加强水坝强度,将坝底从A处向后水平延伸到E处,使新的背水坡的坡度为1:2,求AE的长度(结果精确到1米.参考数据:≈1.414,≈1.732)
7.为方便市民低碳生活绿色出行,市政府计划改造如图所示的人行天桥:天桥的高是10米,原坡面倾斜角∠CAB=45°.
(1)若新坡面倾斜角∠CDB=28°,则新坡面的长CD长是多少?(精确到0.1米)
(2)若新坡角顶点D前留3米的人行道,要使离原坡角顶点A处10米的建筑物不拆除,新坡面的倾斜角∠CDB度数的最小值是多少?(精确到1°)
8.如图,有一段斜坡BC长为10米,坡角∠CBD=12°,为方便残疾人的轮椅车通行,现准备把坡角降为5°.
(1)求坡高CD;
(2)求斜坡新起点A到原起点B的距离(精确到0.1米).
参考数据:sin12°≈0.21,cos12°≈0.98,tan5°≈0.09.
9.如图,天星山山脚下西端A处与东端B处相距800(1+)米,小军和小明同时分别从A处和B处向山顶C匀速行走.已知山的西端的坡角是45°,东端的坡角是30°,小军的行走速度为米/秒.若小明与小军同时到达山顶C处,则小明的行走速度是多少?
三.解直角三角形的应用-仰角俯角问题
10.如图,在热气球C处测得地面A、B两点的俯角分别为30°、45°,热气球C的高度CD为100米,点A、D、B在同一直线上,则AB两点的距离是( )
A.200米 B.200米 C.220米 D.米
11.如图,航拍无人机从A处测得一幢建筑物顶部B的仰角为30°,测得底部C的俯角为60°,此时航拍无人机与该建筑物的水平距离AD为90米,那么该建筑物的高度BC约为 米.(精确到1米,参考数据:≈1.73)
12.如图,楼房BD的前方竖立着旗杆AC.小亮在B处观察旗杆顶端C的仰角为45°,在D处观察旗杆顶端C的俯角为30°,楼高BD为20米.
(1)求∠BCD的度数;
(2)求旗杆AC的高度.
13.如图,在电线杆CD上的C处引拉线CE、CF固定电线杆,拉线CE和地面所成的角∠CED=60°,在离电线杆6米的B处安置高为1.5米的测角仪AB,在A处测得电线杆上C处的仰角为30°,求拉线CE的长(结果保留小数点后一位,参考数据:≈1.41,≈1.73).
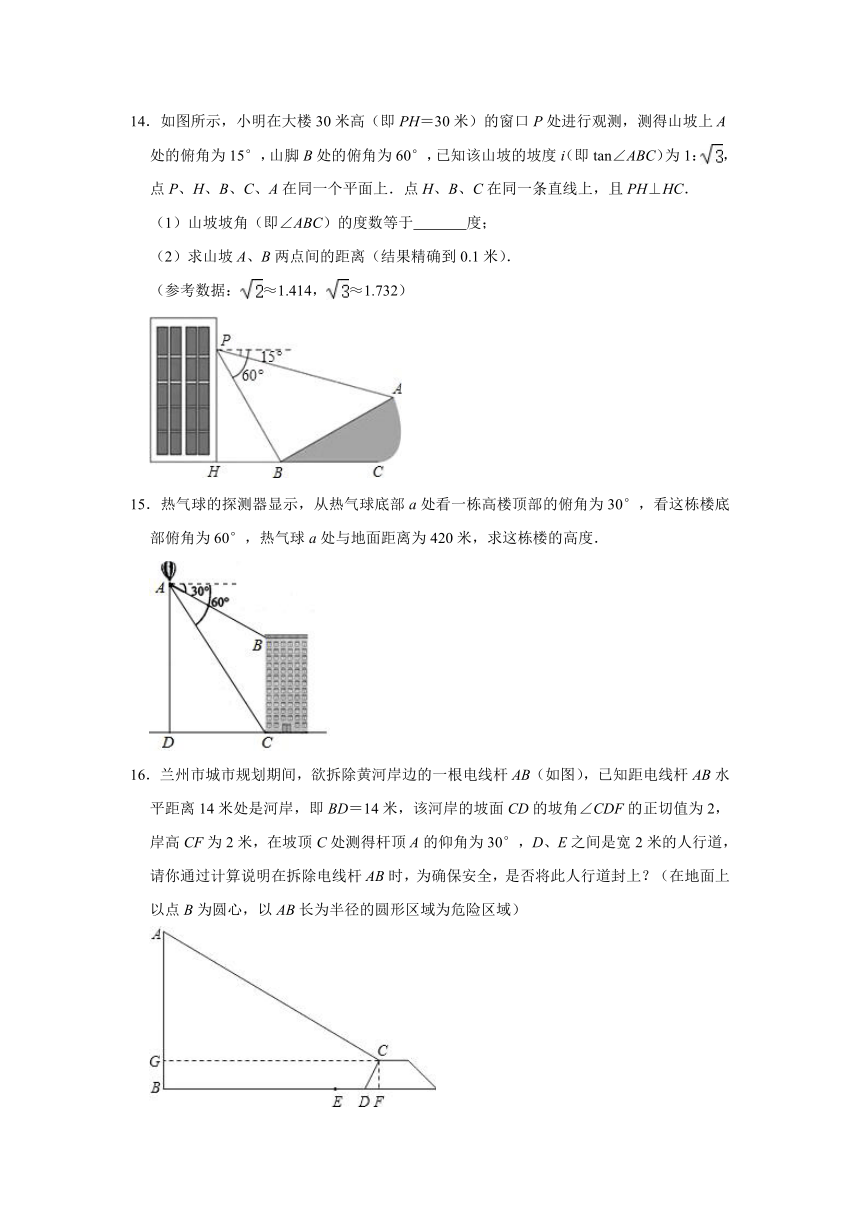
14.如图所示,小明在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的坡度i(即tan∠ABC)为1:,点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上,且PH⊥HC.
(1)山坡坡角(即∠ABC)的度数等于 度;
(2)求山坡A、B两点间的距离(结果精确到0.1米).
(参考数据:≈1.414,≈1.732)
15.热气球的探测器显示,从热气球底部a处看一栋高楼顶部的俯角为30°,看这栋楼底部俯角为60°,热气球a处与地面距离为420米,求这栋楼的高度.
16.兰州市城市规划期间,欲拆除黄河岸边的一根电线杆AB(如图),已知距电线杆AB水平距离14米处是河岸,即BD=14米,该河岸的坡面CD的坡角∠CDF的正切值为2,岸高CF为2米,在坡顶C处测得杆顶A的仰角为30°,D、E之间是宽2米的人行道,请你通过计算说明在拆除电线杆AB时,为确保安全,是否将此人行道封上?(在地面上以点B为圆心,以AB长为半径的圆形区域为危险区域)
四.解直角三角形的应用-方向角问题
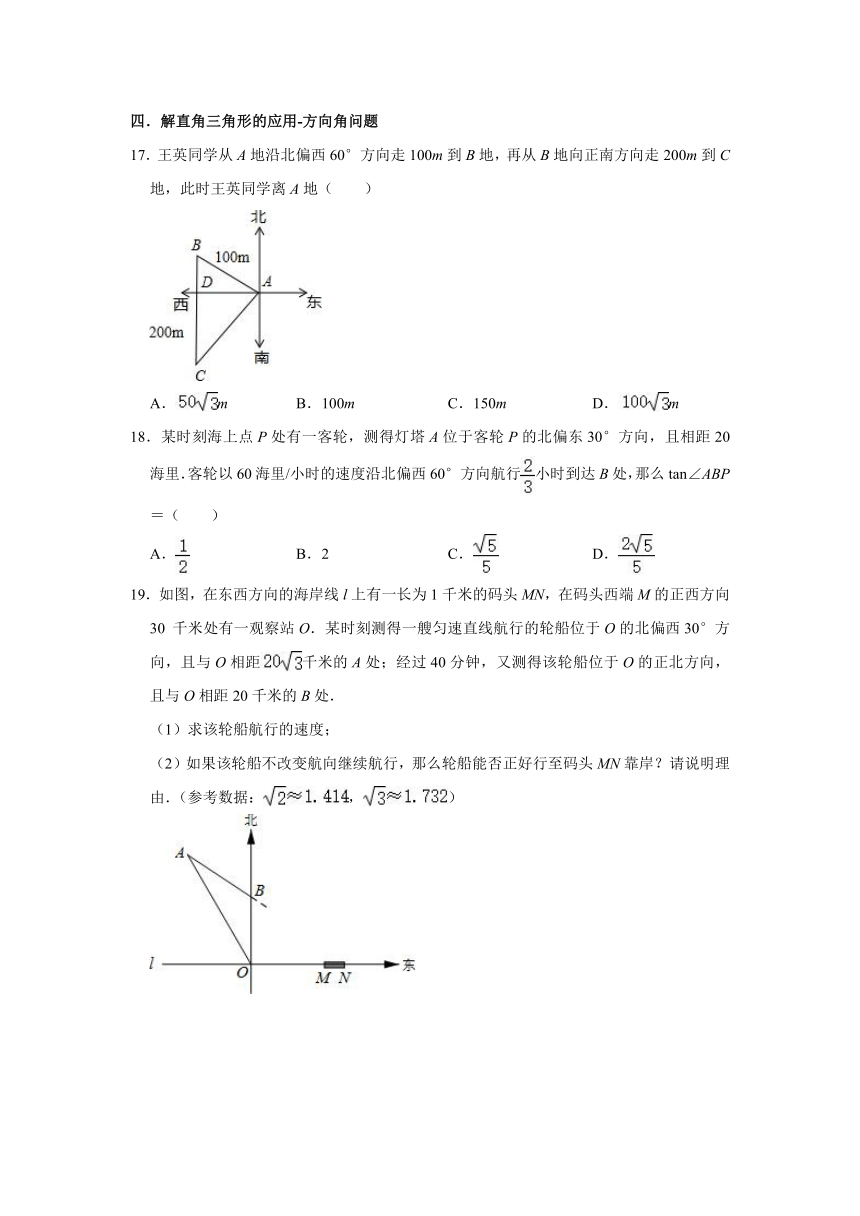
17.王英同学从A地沿北偏西60°方向走100m到B地,再从B地向正南方向走200m到C地,此时王英同学离A地( )
A.m B.100m C.150m D.m
18.某时刻海上点P处有一客轮,测得灯塔A位于客轮P的北偏东30°方向,且相距20海里.客轮以60海里/小时的速度沿北偏西60°方向航行小时到达B处,那么tan∠ABP=( )
A. B.2 C. D.
19.如图,在东西方向的海岸线l上有一长为1千米的码头MN,在码头西端M的正西方向30 千米处有一观察站O.某时刻测得一艘匀速直线航行的轮船位于O的北偏西30°方向,且与O相距千米的A处;经过40分钟,又测得该轮船位于O的正北方向,且与O相距20千米的B处.
(1)求该轮船航行的速度;
(2)如果该轮船不改变航向继续航行,那么轮船能否正好行至码头MN靠岸?请说明理由.(参考数据:,)
20.由我国完全自主设计、自主建造的首艘国产航母于2018年5月成功完成第一次海上试验任务.如图,航母由西向东航行,到达A处时,测得小岛B位于它的北偏东30°方向,且与航母相距80海里再航行一段时间后到达C处,测得小岛B位于它的西北方向,求此时航母与小岛的距离BC的长.
21.如图,港口B位于港口A的南偏东37°方向,灯塔C恰好在AB的中点处.一艘海轮位于港口A的正南方向,港口B的正西方向的D处,它沿正北方向航行5km到达E处,测得灯塔C在北偏东45°方向上,这时,E处距离港口A有多远?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
22.钓鱼岛自古就是中国的领土,我国有关部门已对钓鱼岛及其附属岛屿开展常态化监视监测.M、N为钓鱼岛上东西海岸线上的两点,MN之间的距离约为3.6km,某日,我国一艘海监船从A点沿正北方向巡航,在A点测得岛屿的西端点N在点A的北偏东35°方向;海监船继续航行4km后到达B点,测得岛屿的东端点M在点B的北偏东60°方向,求点M距离海监船航线的最短距离(结果精确到0.1km,tan35°≈0.7).
23.如图,一般捕鱼船在A处发出求救信号,位于A处正西方向的B处有一艘救援艇决定前去救援,但两船之间有大片暗礁,无法直线到达.救援艇决定马上调整方向,先向北偏东60°方向以每小时30海里的速度航行,同时捕鱼船向正北低速航行.30分钟后,捕鱼船到达距离A处1.5海里的D处,此时救援艇在C处测得D处在南偏东53°的方向上.
(1)求C、D两点的距离;
(2)捕鱼船继续低速向北航行,救援艇决定再次调整航向,沿CE方向前去救援,并且捕鱼船和救援艇同时到达到E处,若两船航速不变,求∠ECD的正弦值.(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈)
24.如图,在某中学教学楼A西南方向510米的C处,有一辆货车以60km/h的速度沿北偏东60°方向的道路CF行驶、
(1)若货车以60km/h的速度行驶时其噪声污染半径为100米,试问教学楼是否受到货车噪声的影响?
(2)假设货车以60km/h的以上速度行驶时,其行驶速度每增加10km/h时其噪声污染半径约增大15米,要使教学楼不受货车的噪声影响,在此路段应该限速多少?(精确到10km/h)
25.一条船在海面上自西向东沿直线航行,在A处测得航标C在北偏东60°方向上,前进100米到达B处,又测得航标C在北偏东45°方向上.
(1)请根据以上描述,画出图形.
(2)已知以航标C为圆心,120米为半径的圆形区域内有浅滩,若这条船继续前进,是否有被浅滩阻碍的危险?为什么?
26.如图,A,B,C三个粮仓的位置如图所示,A粮仓在B粮仓北偏东26°,180千米处;C粮仓在B粮仓的正东方,A粮仓的正南方.已知A,B两个粮仓原有存粮共450吨,根据灾情需要,现从A粮仓运出该粮仓存粮的支援C粮仓,从B粮仓运出该粮仓存粮的支援C粮仓,这时A,B两处粮仓的存粮吨数相等.(sin26°=0.44,cos26°=0.90,tan26°=0.49)
(1)A,B两处粮仓原有存粮各多少吨?
(2)C粮仓至少需要支援200吨粮食,问此调拨计划能满足C粮仓的需求吗?
(3)由于气象条件恶劣,从B处出发到C处的车队来回都限速以每小时35公里的速度匀速行驶,而司机小王的汽车油箱的油量最多可行驶4小时,那么小王在途中是否需要加油才能安全地回到B地?请你说明理由.
27.如图,台风中心位于点P,并沿东北方向PQ移动,已知台风移动的速度为30千米/时,受影响区域的半径为200千米,B市位于点P的北偏东75°方向上,距离点P点320千米处.
(1)说明本次台风会影响B市;
(2)求这次台风影响B市的时间.
参考答案
一.解直角三角形的应用
1.解:(1)过M作MN⊥AB,
在Rt△AMN中,AM=10,∠MAN=45°,
∴sin∠MAN=,即,
解得:MN=10,
则测速点M到该公路的距离为10米;
(2)由(1)知:AN=MN=10米,
在Rt△MNB中,∠MBN=37°,
由tan∠MBN=,得:,
解得:BN=13(米),
∴AB=AN+NB=10+13≈23.3(米),
∴汽车从A到B的平均速度为23.3÷2=11.65(米/秒),
∵11.65米/秒=41.94千米/时>40千米/时,
∴此车超速
二.解直角三角形的应用-坡度坡角问题
2.解:河堤横断面迎水坡AB的坡比是1:,
即tan∠BAC===,
∴∠BAC=30°,
∴AB=2BC=2×5=10m,
故选:A.
3.解:根据题意得:=1:,
解得:AC=BC=10(米).
故选:D.
4.解:过点C作CE⊥AD于点E,
∵BC=6m,坝高为14m,
∴AE=6m,CE=14m,
∵斜坡CD的坡度i=1:2,
∴CE:DE=1:2,
∴DE=28m,
则AD=AE+DE=6+28=34(m).
故选:B.
5.解:∵∠BCA=90°,tan∠BAC=,BC=30m,
∴tan∠BAC=,
解得,AC=75,
故选:A.
6.解:作BH⊥AD于H,
在Rt△ABH中,sin∠BAH=,
则BH=AB sin∠BAH=20×=10,AH=AB=10,
在Rt△EBH中,BE的坡度为1:2,BH=10,
∴EH=20,
∴AE=EH﹣AH=20﹣10≈25(米),
答:AE的长度约为25米.
7.(1)在Rt△BCD中,
∵BC=10,∠CDB=28°,
∴CD==≈21.3(米),
答:新坡面的长为21.3米
(2)∵∠CAB=45°,
∴AB=CB=10,
又建筑物离原坡角顶点A处10米,即建筑物离天桥底点B的距离为20米,
当DB取最大值时,∠CDB达最小值,
要使建筑物不被拆掉DB的最大值为20﹣3=17,
则tan∠CDB==≈0.588,
∴∠CDB≈31°.
答:若新坡角顶点D前留3米的人行道,要使离原坡角顶点A处10米的建筑物不拆除,新坡面的倾斜角的最小值是31°.
8.解:(1)在Rt△BCD中,CD=BCsin12°≈10×0.21=2.1米.
(2)在Rt△BCD中,BD=BCcos12°≈10×0.98=9.8米;
在Rt△ACD中,米,
AB=AD﹣BD≈23.33﹣9.8=13.53≈13.5米.
答:坡高2.1米,斜坡新起点与原起点的距离为13.5米.
9.解:过点C作CD⊥AB于点D,设AD=x米,小明的行走速度是a米/秒,
∵∠A=45°,CD⊥AB,
∴AD=CD=x米,
∴AC=x.
在Rt△BCD中,
∵∠B=30°,
∴BC===2x,
∵小军的行走速度为米/秒.若小明与小军同时到达山顶C处,
∴=,解得a=1米/秒.
答:小明的行走速度是1米/秒.
三.解直角三角形的应用-仰角俯角问题
10.解:∵在热气球C处测得地面B点的俯角为45°,
∴BD=CD=100米,
∵在热气球C处测得地面A点的俯角为30°,
∴AC=2×100=200米,
∴AD==100米,
∴AB=AD+BD=100+100=100(1+)米,
故选:D.
11.解:由题意可得:tan30°===,
解得:BD=30(m),
tan60°===,
解得:DC=90(m),
故该建筑物的高度为:BC=BD+DC=120≈208(m),
故答案为:208.
12.解:(1)过点C作CE⊥BD于E,则DF∥CE,AB∥CE
∵DF∥CE
∴∠ECD=∠CDF=30°
同理∠ECB=∠ABC=45°
∴∠BCD=∠ECD+∠ECB=75°.
(2)在Rt△ECD中,∠ECD=30°
∵
∴
同理BE=CE
∵BD=BE+DE
∴,
答:(1)∠BCD为75°;
(2)旗杆AC的高度CE为米.
13.解:过点A作AH⊥CD,垂足为H,
由题意可知四边形ABDH为矩形,∠CAH=30°,
∴AB=DH=1.5(米),BD=AH=6(米),
在Rt△ACH中,tan∠CAH=,
∴CH=AH tan∠CAH,
∴CH=AH tan∠CAH=6tan30°=6×(米),
∵DH=1.5(米),
∴CD=(2+1.5)(米),
在Rt△CDE中,
∵∠CED=60°,sin∠CED=,
∴CE==4+≈5.7(米),
答:拉线CE的长约为5.7米.
14.解:(1)过A作AD⊥BC于D,
∵山坡的坡度i(即tan∠ABC)为1:,
∴∠ABC=30°,
故答案为:30;
(2)由题意得,∠PBH=60°,∠APB=45°,
∵∠ABC=30°,
∴∠ABP=90°,
∴△PBA是等腰直角三角形,
∴PB====20,
∵AB=PB=20=34.6,
答:山坡A、B两点间的距离是34.6米.
15.解:过A作AE⊥BC,交CB的延长线于点E,
在Rt△ACD中,
∵∠CAD=30°,AD=420米,
∴CD=AD tan30°=420×=140(米),
∴AE=CD=140米.
在Rt△ABE中,
∵∠BAE=30°,AE=140米,
∴BE=AE tan30°=140×=140(米),
∴BC=AD﹣BE=420﹣140=280(米),
答:这栋楼的高度为280米.
16.解:由tan∠CDF==2,CF=2米,
∴DF=1米,BG=2米;
∵BD=14米,
∴BF=GC=15米;
在Rt△AGC中,由tan30°=,
∴AG=15×=≈5×1.732=8.660米;
∴AB=8.660+2=10.66米;
而BE=BD﹣ED=12米,
∴BE>AB;
因此不需要封人行道.
四.解直角三角形的应用-方向角问题
17.解:AD=AB sin60°=50;
BD=AB cos60°=50,∴CD=150.
∴AC==100.
故选:D.
18.解:∵灯塔A位于客轮P的北偏东30°方向,且相距20海里.
∴PA=20海里,
∵客轮以60海里/小时的速度沿北偏西60°方向航行小时到达B处,
∴∠APB=90°,BP=60×=40海里,
∴tan∠ABP===.
故选:A.
19.解(1)过点A作AC⊥OB于点C.由题意,得
OA=千米,OB=20千米,∠AOC=30°.
∴(千米).
∵在Rt△AOC中,OC=OA cos∠AOC==30(千米).
∴BC=OC﹣OB=30﹣20=10(千米).
∴在Rt△ABC中,==20(千米).
∴轮船航行的速度为:(千米/时).
(2)如果该轮船不改变航向继续航行,不能行至码头MN靠岸.
理由:延长AB交l于点D.
∵AB=OB=20(千米),∠AOC=30°.
∴∠OAB=∠AOC=30°,∴∠OBD=∠OAB+∠AOC=60°.
∴在Rt△BOD中,OD=OB tan∠OBD=20×tan60°=(千米).
∵>30+1,
∴该轮船不改变航向继续航行,不能行至码头MN靠岸.
20.解:过点B作BD⊥AC于点D,
由题意,得:∠BAD=60°,∠BCD=45°,AB=80,
在Rt△ADB中,∠BAD=60°,
∴BD=AB=40(海里),
在Rt△BCD中,∠BCD=45°,
∴BD=CD=40(海里),
∴BC=BD=40(海里),
答:BC的距离是40海里.
21.解:如图作CH⊥AD于H.设CH=xkm,
在Rt△ACH中,∠A=37°,∵tan37°=,
∴AH==,
在Rt△CEH中,∵∠CEH=45°,
∴CH=EH=x,
∵CH⊥AD,BD⊥AD,
∴CH∥BD,
∴=,
∵AC=CB,
∴AH=HD,
∴=x+5,
∴x=≈15,
∴AE=AH+HE=+15≈35km,
∴E处距离港口A有35km.
22.解:如图,延长MN交AB于K.设KN=x,KB=y,
在Rt△MBK中,tan60°=,
∴x+3.6=y①
在Rt△ANK中,tan35°=,
∴x=0.7(4+y) ②,
由①②可得x=7.1(km),
∴MK=7.1+3.6=10.7(km),
答:点M距离海监船航线的最短距离为10.7km.
23.解:(1)过点C、D分别作CG⊥AB,DF⊥CG,垂足分别为G,F,
∵在Rt△CGB中,∠CBG=90°﹣60°=30°,
∴CG=BC=×(30×)=7.5海里,
∵∠DAG=90°,
∴四边形ADFG是矩形,
∴GF=AD=1.5海里,
∴CF=CG﹣GF=7.5﹣1.5=6海里,
在Rt△CDF中,∠CFD=90°,
∵∠DCF=53°,
∴COS∠DCF=,
∴CD===10(海里).
答:CD两点的距离是10海里;
(2)如图,设渔政船调整方向后t小时能与捕渔船相会合,
由题意知CE=30t,DE=1.5×2×t=3t,∠EDC=53°,
过点E作EH⊥CD于点H,则∠EHD=∠CHE=90°,
∴sin∠EDH=,
∴EH=EDsin53°=3t×0.8=2.4t,
∴在Rt△EHC中,sin∠ECD===0.08.
答:∠ECD的正弦值是0.08.
24.解:(1)A教学楼不受货车的噪声影响.
作AH⊥CF于H,则∠ACH=15°,
在Rt△ACH中,∵AC=510,
∴AH=AC×sin15°=510×0.26=132(米).
∵132>100,
∴A教学楼不受大货车的噪声影响.
(2)设在此路段应该限速xkm/h,由题意有:,
解得:x<81,因此在此路段应该限速80km/h.
(只要能用数学知识说明在此路段应该限速80km/h即可给满分)
25.解:(1)
(2)答:这条船继续前进,没有被浅滩阻碍的危险.
作CD⊥直线AB于点D,
由已知可得∠CAD=30°,∠CBD=45°,
AB=100米.
设CD=x米.
在Rt△ACD中,tan∠CAD=,
∴AD=,
在Rt△CBD中,∵∠CBD=45°,
∴BD=CD=x,
∵AD﹣BD=AB,
∴,
解得,
∴这条船继续前进没有被浅滩阻碍的危险.
26.解:
(1)设A,B两处粮仓原有存粮x,y吨
根据题意得:
解得:x=270,y=180.
答:A,B两处粮仓原有存粮分别是270,180吨.
(2)A粮仓支援C粮仓的粮食是×270=162(吨),
B粮仓支援C粮仓的粮食是×180=72(吨),
A,B两粮仓合计共支援C粮仓粮食为162+72=234(吨).
∵234>200,
∴此次调拨能满足C粮仓需求.
(3)根据题意知:∠A=26°,AB=180千米,∠ACB=90°.
在Rt△ABC中,sin∠BAC=,
∴BC=AB sin∠BAC=180×0.44=79.2.
∵此车最多可行驶4×35=140(千米)<2×79.2,
∴小王途中须加油才能安全回到B地.
27.(1)如图所示:
∵台风中心位于点P,并沿东北方向PQ移动,B市位于点P的北偏东75°方向上,
∴∠QPG=45°,∠NPB=75°,∠BPG=15°,
∴∠BPQ=30°
作BH⊥PQ于点H,在Rt△BHP中,由条件知,PB=320,
得 BH=320sin30°=160<200,
∴本次台风会影响B市.
(2)如图,若台风中心移动到P1时,台风开始影响B市,台风中心移动到P2时,台风影响结束.由(1)得BH=160,由条件得BP1=BP2=200,
∴P1P2=2=240,
∴台风影响的时间t==8(小时).
一.解直角三角形的应用
1.根据道路管理规定,在广州某段笔直公路上行驶的车辆,限速40千米/时;已知交警测速点M到该公路A点的距离为10米,∠MAB=45°,∠MBA=37°(如图所示),现有一辆汽车由A往B方向匀速行驶,测得此车从A点行驶到B点所用的时间为2秒.
(1)求测速点M到该公路的距离.
(2)通过计算判断此车是否超速.(数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
二.解直角三角形的应用-坡度坡角问题
2.如图所示,河堤横断面迎水坡AB的坡比是1:,堤高BC=5m,则坡面AB的长是( )
A.10m B.m C.15m D.m
3.江堤的横断面如图,堤高BC=10米,迎水坡AB的坡比是1:,则堤脚AC的长是( )
A.20米 B.20米 C.米 D.10米
4.如图,一小型水库堤坝的横断面为直角梯形,坝顶BC宽6m,坝高14m,斜坡CD的坡度i=1:2,则坝底AD的长为( )
A.13m B.34m C.(6+)m D.40m
5.如图,有一斜坡AB,坡顶B离地面的高度BC为30m,斜坡的倾斜角是∠BAC,若tan∠BAC=,则此斜坡的水平距离AC为( )
A.75m B.50m C.30m D.12m
6.如图,水坝的横断面是梯形ABCD,背水坡AB的坡角∠BAD=60°,坡长AB=20m,为加强水坝强度,将坝底从A处向后水平延伸到E处,使新的背水坡的坡度为1:2,求AE的长度(结果精确到1米.参考数据:≈1.414,≈1.732)
7.为方便市民低碳生活绿色出行,市政府计划改造如图所示的人行天桥:天桥的高是10米,原坡面倾斜角∠CAB=45°.
(1)若新坡面倾斜角∠CDB=28°,则新坡面的长CD长是多少?(精确到0.1米)
(2)若新坡角顶点D前留3米的人行道,要使离原坡角顶点A处10米的建筑物不拆除,新坡面的倾斜角∠CDB度数的最小值是多少?(精确到1°)
8.如图,有一段斜坡BC长为10米,坡角∠CBD=12°,为方便残疾人的轮椅车通行,现准备把坡角降为5°.
(1)求坡高CD;
(2)求斜坡新起点A到原起点B的距离(精确到0.1米).
参考数据:sin12°≈0.21,cos12°≈0.98,tan5°≈0.09.
9.如图,天星山山脚下西端A处与东端B处相距800(1+)米,小军和小明同时分别从A处和B处向山顶C匀速行走.已知山的西端的坡角是45°,东端的坡角是30°,小军的行走速度为米/秒.若小明与小军同时到达山顶C处,则小明的行走速度是多少?
三.解直角三角形的应用-仰角俯角问题
10.如图,在热气球C处测得地面A、B两点的俯角分别为30°、45°,热气球C的高度CD为100米,点A、D、B在同一直线上,则AB两点的距离是( )
A.200米 B.200米 C.220米 D.米
11.如图,航拍无人机从A处测得一幢建筑物顶部B的仰角为30°,测得底部C的俯角为60°,此时航拍无人机与该建筑物的水平距离AD为90米,那么该建筑物的高度BC约为 米.(精确到1米,参考数据:≈1.73)
12.如图,楼房BD的前方竖立着旗杆AC.小亮在B处观察旗杆顶端C的仰角为45°,在D处观察旗杆顶端C的俯角为30°,楼高BD为20米.
(1)求∠BCD的度数;
(2)求旗杆AC的高度.
13.如图,在电线杆CD上的C处引拉线CE、CF固定电线杆,拉线CE和地面所成的角∠CED=60°,在离电线杆6米的B处安置高为1.5米的测角仪AB,在A处测得电线杆上C处的仰角为30°,求拉线CE的长(结果保留小数点后一位,参考数据:≈1.41,≈1.73).
14.如图所示,小明在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的坡度i(即tan∠ABC)为1:,点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上,且PH⊥HC.
(1)山坡坡角(即∠ABC)的度数等于 度;
(2)求山坡A、B两点间的距离(结果精确到0.1米).
(参考数据:≈1.414,≈1.732)
15.热气球的探测器显示,从热气球底部a处看一栋高楼顶部的俯角为30°,看这栋楼底部俯角为60°,热气球a处与地面距离为420米,求这栋楼的高度.
16.兰州市城市规划期间,欲拆除黄河岸边的一根电线杆AB(如图),已知距电线杆AB水平距离14米处是河岸,即BD=14米,该河岸的坡面CD的坡角∠CDF的正切值为2,岸高CF为2米,在坡顶C处测得杆顶A的仰角为30°,D、E之间是宽2米的人行道,请你通过计算说明在拆除电线杆AB时,为确保安全,是否将此人行道封上?(在地面上以点B为圆心,以AB长为半径的圆形区域为危险区域)
四.解直角三角形的应用-方向角问题
17.王英同学从A地沿北偏西60°方向走100m到B地,再从B地向正南方向走200m到C地,此时王英同学离A地( )
A.m B.100m C.150m D.m
18.某时刻海上点P处有一客轮,测得灯塔A位于客轮P的北偏东30°方向,且相距20海里.客轮以60海里/小时的速度沿北偏西60°方向航行小时到达B处,那么tan∠ABP=( )
A. B.2 C. D.
19.如图,在东西方向的海岸线l上有一长为1千米的码头MN,在码头西端M的正西方向30 千米处有一观察站O.某时刻测得一艘匀速直线航行的轮船位于O的北偏西30°方向,且与O相距千米的A处;经过40分钟,又测得该轮船位于O的正北方向,且与O相距20千米的B处.
(1)求该轮船航行的速度;
(2)如果该轮船不改变航向继续航行,那么轮船能否正好行至码头MN靠岸?请说明理由.(参考数据:,)
20.由我国完全自主设计、自主建造的首艘国产航母于2018年5月成功完成第一次海上试验任务.如图,航母由西向东航行,到达A处时,测得小岛B位于它的北偏东30°方向,且与航母相距80海里再航行一段时间后到达C处,测得小岛B位于它的西北方向,求此时航母与小岛的距离BC的长.
21.如图,港口B位于港口A的南偏东37°方向,灯塔C恰好在AB的中点处.一艘海轮位于港口A的正南方向,港口B的正西方向的D处,它沿正北方向航行5km到达E处,测得灯塔C在北偏东45°方向上,这时,E处距离港口A有多远?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
22.钓鱼岛自古就是中国的领土,我国有关部门已对钓鱼岛及其附属岛屿开展常态化监视监测.M、N为钓鱼岛上东西海岸线上的两点,MN之间的距离约为3.6km,某日,我国一艘海监船从A点沿正北方向巡航,在A点测得岛屿的西端点N在点A的北偏东35°方向;海监船继续航行4km后到达B点,测得岛屿的东端点M在点B的北偏东60°方向,求点M距离海监船航线的最短距离(结果精确到0.1km,tan35°≈0.7).
23.如图,一般捕鱼船在A处发出求救信号,位于A处正西方向的B处有一艘救援艇决定前去救援,但两船之间有大片暗礁,无法直线到达.救援艇决定马上调整方向,先向北偏东60°方向以每小时30海里的速度航行,同时捕鱼船向正北低速航行.30分钟后,捕鱼船到达距离A处1.5海里的D处,此时救援艇在C处测得D处在南偏东53°的方向上.
(1)求C、D两点的距离;
(2)捕鱼船继续低速向北航行,救援艇决定再次调整航向,沿CE方向前去救援,并且捕鱼船和救援艇同时到达到E处,若两船航速不变,求∠ECD的正弦值.(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈)
24.如图,在某中学教学楼A西南方向510米的C处,有一辆货车以60km/h的速度沿北偏东60°方向的道路CF行驶、
(1)若货车以60km/h的速度行驶时其噪声污染半径为100米,试问教学楼是否受到货车噪声的影响?
(2)假设货车以60km/h的以上速度行驶时,其行驶速度每增加10km/h时其噪声污染半径约增大15米,要使教学楼不受货车的噪声影响,在此路段应该限速多少?(精确到10km/h)
25.一条船在海面上自西向东沿直线航行,在A处测得航标C在北偏东60°方向上,前进100米到达B处,又测得航标C在北偏东45°方向上.
(1)请根据以上描述,画出图形.
(2)已知以航标C为圆心,120米为半径的圆形区域内有浅滩,若这条船继续前进,是否有被浅滩阻碍的危险?为什么?
26.如图,A,B,C三个粮仓的位置如图所示,A粮仓在B粮仓北偏东26°,180千米处;C粮仓在B粮仓的正东方,A粮仓的正南方.已知A,B两个粮仓原有存粮共450吨,根据灾情需要,现从A粮仓运出该粮仓存粮的支援C粮仓,从B粮仓运出该粮仓存粮的支援C粮仓,这时A,B两处粮仓的存粮吨数相等.(sin26°=0.44,cos26°=0.90,tan26°=0.49)
(1)A,B两处粮仓原有存粮各多少吨?
(2)C粮仓至少需要支援200吨粮食,问此调拨计划能满足C粮仓的需求吗?
(3)由于气象条件恶劣,从B处出发到C处的车队来回都限速以每小时35公里的速度匀速行驶,而司机小王的汽车油箱的油量最多可行驶4小时,那么小王在途中是否需要加油才能安全地回到B地?请你说明理由.
27.如图,台风中心位于点P,并沿东北方向PQ移动,已知台风移动的速度为30千米/时,受影响区域的半径为200千米,B市位于点P的北偏东75°方向上,距离点P点320千米处.
(1)说明本次台风会影响B市;
(2)求这次台风影响B市的时间.
参考答案
一.解直角三角形的应用
1.解:(1)过M作MN⊥AB,
在Rt△AMN中,AM=10,∠MAN=45°,
∴sin∠MAN=,即,
解得:MN=10,
则测速点M到该公路的距离为10米;
(2)由(1)知:AN=MN=10米,
在Rt△MNB中,∠MBN=37°,
由tan∠MBN=,得:,
解得:BN=13(米),
∴AB=AN+NB=10+13≈23.3(米),
∴汽车从A到B的平均速度为23.3÷2=11.65(米/秒),
∵11.65米/秒=41.94千米/时>40千米/时,
∴此车超速
二.解直角三角形的应用-坡度坡角问题
2.解:河堤横断面迎水坡AB的坡比是1:,
即tan∠BAC===,
∴∠BAC=30°,
∴AB=2BC=2×5=10m,
故选:A.
3.解:根据题意得:=1:,
解得:AC=BC=10(米).
故选:D.
4.解:过点C作CE⊥AD于点E,
∵BC=6m,坝高为14m,
∴AE=6m,CE=14m,
∵斜坡CD的坡度i=1:2,
∴CE:DE=1:2,
∴DE=28m,
则AD=AE+DE=6+28=34(m).
故选:B.
5.解:∵∠BCA=90°,tan∠BAC=,BC=30m,
∴tan∠BAC=,
解得,AC=75,
故选:A.
6.解:作BH⊥AD于H,
在Rt△ABH中,sin∠BAH=,
则BH=AB sin∠BAH=20×=10,AH=AB=10,
在Rt△EBH中,BE的坡度为1:2,BH=10,
∴EH=20,
∴AE=EH﹣AH=20﹣10≈25(米),
答:AE的长度约为25米.
7.(1)在Rt△BCD中,
∵BC=10,∠CDB=28°,
∴CD==≈21.3(米),
答:新坡面的长为21.3米
(2)∵∠CAB=45°,
∴AB=CB=10,
又建筑物离原坡角顶点A处10米,即建筑物离天桥底点B的距离为20米,
当DB取最大值时,∠CDB达最小值,
要使建筑物不被拆掉DB的最大值为20﹣3=17,
则tan∠CDB==≈0.588,
∴∠CDB≈31°.
答:若新坡角顶点D前留3米的人行道,要使离原坡角顶点A处10米的建筑物不拆除,新坡面的倾斜角的最小值是31°.
8.解:(1)在Rt△BCD中,CD=BCsin12°≈10×0.21=2.1米.
(2)在Rt△BCD中,BD=BCcos12°≈10×0.98=9.8米;
在Rt△ACD中,米,
AB=AD﹣BD≈23.33﹣9.8=13.53≈13.5米.
答:坡高2.1米,斜坡新起点与原起点的距离为13.5米.
9.解:过点C作CD⊥AB于点D,设AD=x米,小明的行走速度是a米/秒,
∵∠A=45°,CD⊥AB,
∴AD=CD=x米,
∴AC=x.
在Rt△BCD中,
∵∠B=30°,
∴BC===2x,
∵小军的行走速度为米/秒.若小明与小军同时到达山顶C处,
∴=,解得a=1米/秒.
答:小明的行走速度是1米/秒.
三.解直角三角形的应用-仰角俯角问题
10.解:∵在热气球C处测得地面B点的俯角为45°,
∴BD=CD=100米,
∵在热气球C处测得地面A点的俯角为30°,
∴AC=2×100=200米,
∴AD==100米,
∴AB=AD+BD=100+100=100(1+)米,
故选:D.
11.解:由题意可得:tan30°===,
解得:BD=30(m),
tan60°===,
解得:DC=90(m),
故该建筑物的高度为:BC=BD+DC=120≈208(m),
故答案为:208.
12.解:(1)过点C作CE⊥BD于E,则DF∥CE,AB∥CE
∵DF∥CE
∴∠ECD=∠CDF=30°
同理∠ECB=∠ABC=45°
∴∠BCD=∠ECD+∠ECB=75°.
(2)在Rt△ECD中,∠ECD=30°
∵
∴
同理BE=CE
∵BD=BE+DE
∴,
答:(1)∠BCD为75°;
(2)旗杆AC的高度CE为米.
13.解:过点A作AH⊥CD,垂足为H,
由题意可知四边形ABDH为矩形,∠CAH=30°,
∴AB=DH=1.5(米),BD=AH=6(米),
在Rt△ACH中,tan∠CAH=,
∴CH=AH tan∠CAH,
∴CH=AH tan∠CAH=6tan30°=6×(米),
∵DH=1.5(米),
∴CD=(2+1.5)(米),
在Rt△CDE中,
∵∠CED=60°,sin∠CED=,
∴CE==4+≈5.7(米),
答:拉线CE的长约为5.7米.
14.解:(1)过A作AD⊥BC于D,
∵山坡的坡度i(即tan∠ABC)为1:,
∴∠ABC=30°,
故答案为:30;
(2)由题意得,∠PBH=60°,∠APB=45°,
∵∠ABC=30°,
∴∠ABP=90°,
∴△PBA是等腰直角三角形,
∴PB====20,
∵AB=PB=20=34.6,
答:山坡A、B两点间的距离是34.6米.
15.解:过A作AE⊥BC,交CB的延长线于点E,
在Rt△ACD中,
∵∠CAD=30°,AD=420米,
∴CD=AD tan30°=420×=140(米),
∴AE=CD=140米.
在Rt△ABE中,
∵∠BAE=30°,AE=140米,
∴BE=AE tan30°=140×=140(米),
∴BC=AD﹣BE=420﹣140=280(米),
答:这栋楼的高度为280米.
16.解:由tan∠CDF==2,CF=2米,
∴DF=1米,BG=2米;
∵BD=14米,
∴BF=GC=15米;
在Rt△AGC中,由tan30°=,
∴AG=15×=≈5×1.732=8.660米;
∴AB=8.660+2=10.66米;
而BE=BD﹣ED=12米,
∴BE>AB;
因此不需要封人行道.
四.解直角三角形的应用-方向角问题
17.解:AD=AB sin60°=50;
BD=AB cos60°=50,∴CD=150.
∴AC==100.
故选:D.
18.解:∵灯塔A位于客轮P的北偏东30°方向,且相距20海里.
∴PA=20海里,
∵客轮以60海里/小时的速度沿北偏西60°方向航行小时到达B处,
∴∠APB=90°,BP=60×=40海里,
∴tan∠ABP===.
故选:A.
19.解(1)过点A作AC⊥OB于点C.由题意,得
OA=千米,OB=20千米,∠AOC=30°.
∴(千米).
∵在Rt△AOC中,OC=OA cos∠AOC==30(千米).
∴BC=OC﹣OB=30﹣20=10(千米).
∴在Rt△ABC中,==20(千米).
∴轮船航行的速度为:(千米/时).
(2)如果该轮船不改变航向继续航行,不能行至码头MN靠岸.
理由:延长AB交l于点D.
∵AB=OB=20(千米),∠AOC=30°.
∴∠OAB=∠AOC=30°,∴∠OBD=∠OAB+∠AOC=60°.
∴在Rt△BOD中,OD=OB tan∠OBD=20×tan60°=(千米).
∵>30+1,
∴该轮船不改变航向继续航行,不能行至码头MN靠岸.
20.解:过点B作BD⊥AC于点D,
由题意,得:∠BAD=60°,∠BCD=45°,AB=80,
在Rt△ADB中,∠BAD=60°,
∴BD=AB=40(海里),
在Rt△BCD中,∠BCD=45°,
∴BD=CD=40(海里),
∴BC=BD=40(海里),
答:BC的距离是40海里.
21.解:如图作CH⊥AD于H.设CH=xkm,
在Rt△ACH中,∠A=37°,∵tan37°=,
∴AH==,
在Rt△CEH中,∵∠CEH=45°,
∴CH=EH=x,
∵CH⊥AD,BD⊥AD,
∴CH∥BD,
∴=,
∵AC=CB,
∴AH=HD,
∴=x+5,
∴x=≈15,
∴AE=AH+HE=+15≈35km,
∴E处距离港口A有35km.
22.解:如图,延长MN交AB于K.设KN=x,KB=y,
在Rt△MBK中,tan60°=,
∴x+3.6=y①
在Rt△ANK中,tan35°=,
∴x=0.7(4+y) ②,
由①②可得x=7.1(km),
∴MK=7.1+3.6=10.7(km),
答:点M距离海监船航线的最短距离为10.7km.
23.解:(1)过点C、D分别作CG⊥AB,DF⊥CG,垂足分别为G,F,
∵在Rt△CGB中,∠CBG=90°﹣60°=30°,
∴CG=BC=×(30×)=7.5海里,
∵∠DAG=90°,
∴四边形ADFG是矩形,
∴GF=AD=1.5海里,
∴CF=CG﹣GF=7.5﹣1.5=6海里,
在Rt△CDF中,∠CFD=90°,
∵∠DCF=53°,
∴COS∠DCF=,
∴CD===10(海里).
答:CD两点的距离是10海里;
(2)如图,设渔政船调整方向后t小时能与捕渔船相会合,
由题意知CE=30t,DE=1.5×2×t=3t,∠EDC=53°,
过点E作EH⊥CD于点H,则∠EHD=∠CHE=90°,
∴sin∠EDH=,
∴EH=EDsin53°=3t×0.8=2.4t,
∴在Rt△EHC中,sin∠ECD===0.08.
答:∠ECD的正弦值是0.08.
24.解:(1)A教学楼不受货车的噪声影响.
作AH⊥CF于H,则∠ACH=15°,
在Rt△ACH中,∵AC=510,
∴AH=AC×sin15°=510×0.26=132(米).
∵132>100,
∴A教学楼不受大货车的噪声影响.
(2)设在此路段应该限速xkm/h,由题意有:,
解得:x<81,因此在此路段应该限速80km/h.
(只要能用数学知识说明在此路段应该限速80km/h即可给满分)
25.解:(1)
(2)答:这条船继续前进,没有被浅滩阻碍的危险.
作CD⊥直线AB于点D,
由已知可得∠CAD=30°,∠CBD=45°,
AB=100米.
设CD=x米.
在Rt△ACD中,tan∠CAD=,
∴AD=,
在Rt△CBD中,∵∠CBD=45°,
∴BD=CD=x,
∵AD﹣BD=AB,
∴,
解得,
∴这条船继续前进没有被浅滩阻碍的危险.
26.解:
(1)设A,B两处粮仓原有存粮x,y吨
根据题意得:
解得:x=270,y=180.
答:A,B两处粮仓原有存粮分别是270,180吨.
(2)A粮仓支援C粮仓的粮食是×270=162(吨),
B粮仓支援C粮仓的粮食是×180=72(吨),
A,B两粮仓合计共支援C粮仓粮食为162+72=234(吨).
∵234>200,
∴此次调拨能满足C粮仓需求.
(3)根据题意知:∠A=26°,AB=180千米,∠ACB=90°.
在Rt△ABC中,sin∠BAC=,
∴BC=AB sin∠BAC=180×0.44=79.2.
∵此车最多可行驶4×35=140(千米)<2×79.2,
∴小王途中须加油才能安全回到B地.
27.(1)如图所示:
∵台风中心位于点P,并沿东北方向PQ移动,B市位于点P的北偏东75°方向上,
∴∠QPG=45°,∠NPB=75°,∠BPG=15°,
∴∠BPQ=30°
作BH⊥PQ于点H,在Rt△BHP中,由条件知,PB=320,
得 BH=320sin30°=160<200,
∴本次台风会影响B市.
(2)如图,若台风中心移动到P1时,台风开始影响B市,台风中心移动到P2时,台风影响结束.由(1)得BH=160,由条件得BP1=BP2=200,
∴P1P2=2=240,
∴台风影响的时间t==8(小时).
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
