2021--2022学年人教版八年级数学上册11.3.1 多边形 同步练习 (word版含解析)
文档属性
| 名称 | 2021--2022学年人教版八年级数学上册11.3.1 多边形 同步练习 (word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 77.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-01 00:00:00 | ||
图片预览


文档简介
多边形
一、选择题
在凸多边形中,四边形有条对角线,五边形有条对角线,观察探索凸十边形的对角线有
A. 条 B. 条 C. 条 D. 条
下列图形中,是正多边形的是
A. 直角三角形 B. 等腰三角形 C. 长方形 D. 正方形
已知一个多边形从一个顶点处只能引出条对角线,则它是
A. 五边形 B. 六边形 C. 七边形 D. 八边形
下列说法不正确的是
A. 正多边形的各边都相等 B. 正多边形的各内角都相等
C. 正四边形就是长方形 D. 正三角形就是等边三角形
把一个多边形纸片沿一条直线截下一个三角形后,变成一个十八边形,则原多边形纸片的边数不可能是
A. B. C. D.
以线段,,,为边作四边形,可以作
A. 个 B. 个 C. 个 D. 无数个
将一个正方形桌面砍下一个角后,桌子剩下的角的个数是
A. 个 B. 个
C. 个 D. 个或个或个
二、填空题
如图,在四边形中,延长,,则图中四边形的内角有______ ,外角有______ .
如图所示的图形中,属于多边形的有_______个.
从多边形的一个顶点所引的对角线把这个多边形分成个三角形,则这个多边形共有 条对角线.
三、解答题
在如图所示的四边形中,截去一个角后使它变成:三角形四边形五边形,请分别在图中画出截线.
已知正边形的周长为,边长为
当时,请直接写出的值;
把正边形的周长与边数同时增加后,假设得到的仍是正多边形,它的边数为,周长为,边长为有人分别取等于,,,再求出相应的与,然后断言:“无论取任何大于的正整数,与一定不相等.”你认为这种说法对吗?若不对,请求出不符合这一说法的的值.
五边形中,过顶点最多能引几条对角线?它们将五边形分为几个三角形?这几个三角形所有内角之和与五边形内角之和有什么关系?
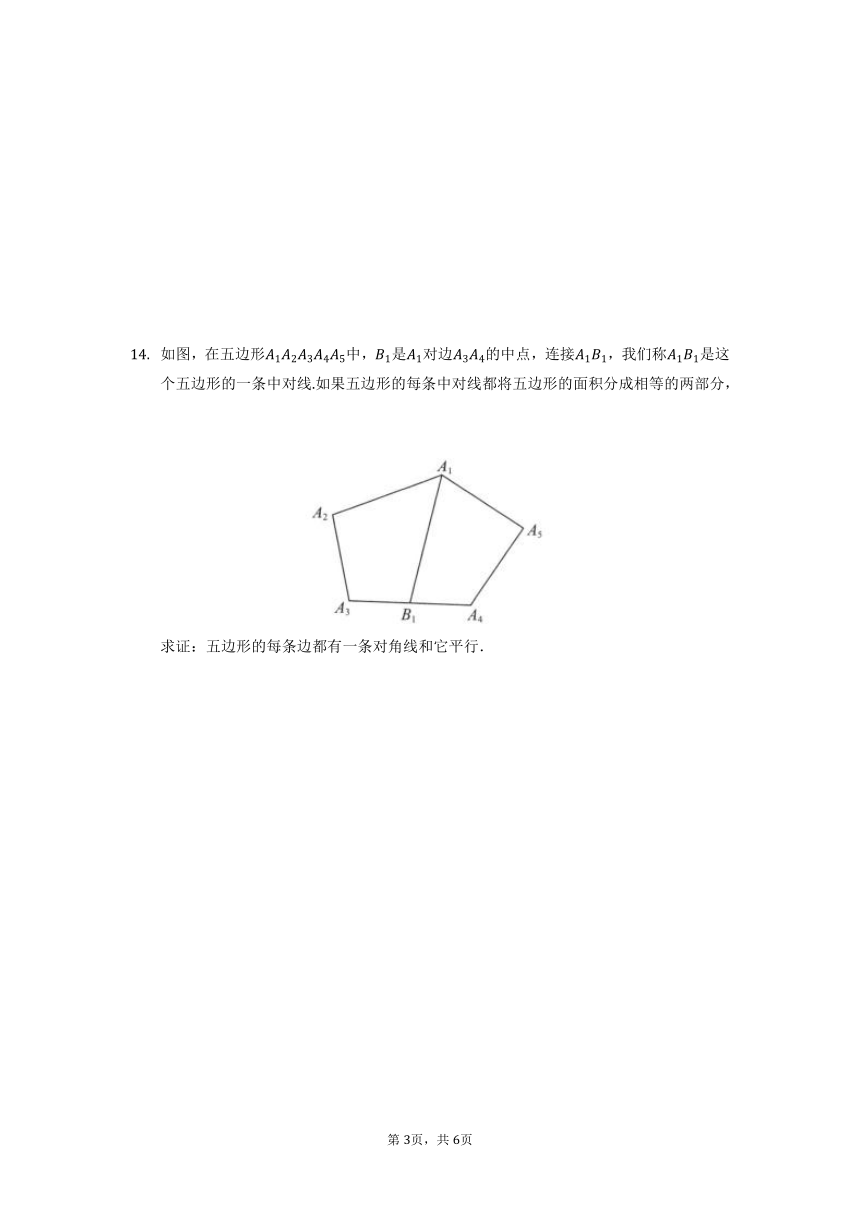
如图,在五边形中,是对边的中点,连接,我们称是这个五边形的一条中对线如果五边形的每条中对线都将五边形的面积分成相等的两部分,求证:五边形的每条边都有一条对角线和它平行.
答案和解析
1.【答案】
2.【答案】
【解析】解:
选项,直角三角形有一个内角是直角,其他两个内角都是锐角,即直角三角形的三个内角不都相等,故不是正多边形;
选项,等腰三角形的三条边不一定都相等,所以不是正多边形;
选项,长方形的四个角都是直角,但是四条边不一定都相等,故不是正多边形;
选项,正方形四个内角都相等,且四条边都相等,所以是正多边形.
故选D.
3.【答案】
【解析】解:多边形从一个顶点出发可引出条对角线,
,
解得.
即这个多边形是七边形,
4.【答案】
5.【答案】
6.【答案】
【解析】解:四条线段组成的四边形可有无数种变化.
7.【答案】
【解析】如图所示.
由图可知,桌子剩下的角的的个数是是个或个或个.
8.【答案】、、、 、
【解析】解:图中四边形的内角有、、、,
外角有、.
故答案为:、、、;、.
根据多边形的内角和外角的定义可得答案.
本题考查四边形的内角与外角,掌握内角与外角的定义是解题关键.
9.【答案】
10.【答案】
11.【答案】解:如图答案不唯一.
12.【答案】解:;
此说法不正确.
理由如下:尽管当、、时,或,
但可令,得,即.
,
解得,
经检验是方程的根.
当时,,即不符合这一说法的的值为.
13.【答案】解:五边形中,过顶点最多能引条对角线,它们将五边形分为个三角形,这几个三角形所有内角之和与五边形内角之和相等.
14.【答案】证明:取中点,连接、、、,
,
,
又四边形与四边形的面积相等,
,
同理,
,
与边上的高相等,
,
同理可证,,,.
即五边形的每条边都有一条对角线和它平行.
第2页,共2页
第1页,共1页
一、选择题
在凸多边形中,四边形有条对角线,五边形有条对角线,观察探索凸十边形的对角线有
A. 条 B. 条 C. 条 D. 条
下列图形中,是正多边形的是
A. 直角三角形 B. 等腰三角形 C. 长方形 D. 正方形
已知一个多边形从一个顶点处只能引出条对角线,则它是
A. 五边形 B. 六边形 C. 七边形 D. 八边形
下列说法不正确的是
A. 正多边形的各边都相等 B. 正多边形的各内角都相等
C. 正四边形就是长方形 D. 正三角形就是等边三角形
把一个多边形纸片沿一条直线截下一个三角形后,变成一个十八边形,则原多边形纸片的边数不可能是
A. B. C. D.
以线段,,,为边作四边形,可以作
A. 个 B. 个 C. 个 D. 无数个
将一个正方形桌面砍下一个角后,桌子剩下的角的个数是
A. 个 B. 个
C. 个 D. 个或个或个
二、填空题
如图,在四边形中,延长,,则图中四边形的内角有______ ,外角有______ .
如图所示的图形中,属于多边形的有_______个.
从多边形的一个顶点所引的对角线把这个多边形分成个三角形,则这个多边形共有 条对角线.
三、解答题
在如图所示的四边形中,截去一个角后使它变成:三角形四边形五边形,请分别在图中画出截线.
已知正边形的周长为,边长为
当时,请直接写出的值;
把正边形的周长与边数同时增加后,假设得到的仍是正多边形,它的边数为,周长为,边长为有人分别取等于,,,再求出相应的与,然后断言:“无论取任何大于的正整数,与一定不相等.”你认为这种说法对吗?若不对,请求出不符合这一说法的的值.
五边形中,过顶点最多能引几条对角线?它们将五边形分为几个三角形?这几个三角形所有内角之和与五边形内角之和有什么关系?
如图,在五边形中,是对边的中点,连接,我们称是这个五边形的一条中对线如果五边形的每条中对线都将五边形的面积分成相等的两部分,求证:五边形的每条边都有一条对角线和它平行.
答案和解析
1.【答案】
2.【答案】
【解析】解:
选项,直角三角形有一个内角是直角,其他两个内角都是锐角,即直角三角形的三个内角不都相等,故不是正多边形;
选项,等腰三角形的三条边不一定都相等,所以不是正多边形;
选项,长方形的四个角都是直角,但是四条边不一定都相等,故不是正多边形;
选项,正方形四个内角都相等,且四条边都相等,所以是正多边形.
故选D.
3.【答案】
【解析】解:多边形从一个顶点出发可引出条对角线,
,
解得.
即这个多边形是七边形,
4.【答案】
5.【答案】
6.【答案】
【解析】解:四条线段组成的四边形可有无数种变化.
7.【答案】
【解析】如图所示.
由图可知,桌子剩下的角的的个数是是个或个或个.
8.【答案】、、、 、
【解析】解:图中四边形的内角有、、、,
外角有、.
故答案为:、、、;、.
根据多边形的内角和外角的定义可得答案.
本题考查四边形的内角与外角,掌握内角与外角的定义是解题关键.
9.【答案】
10.【答案】
11.【答案】解:如图答案不唯一.
12.【答案】解:;
此说法不正确.
理由如下:尽管当、、时,或,
但可令,得,即.
,
解得,
经检验是方程的根.
当时,,即不符合这一说法的的值为.
13.【答案】解:五边形中,过顶点最多能引条对角线,它们将五边形分为个三角形,这几个三角形所有内角之和与五边形内角之和相等.
14.【答案】证明:取中点,连接、、、,
,
,
又四边形与四边形的面积相等,
,
同理,
,
与边上的高相等,
,
同理可证,,,.
即五边形的每条边都有一条对角线和它平行.
第2页,共2页
第1页,共1页
