人教版2021-2022学年九年级数学上册22.3实际问题与二次函数同步练习(word解析版)
文档属性
| 名称 | 人教版2021-2022学年九年级数学上册22.3实际问题与二次函数同步练习(word解析版) |  | |
| 格式 | docx | ||
| 文件大小 | 404.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-01 09:22:21 | ||
图片预览




文档简介
2021-2022学年九年级数学上册(人教版)教材同步
22.3实际问题与二次函数-同步练习
时间:60分钟
一、单选题
1.飞机着陆后滑行的距离y(单位:m)关于滑行时间以(单位:)的函数解析式是y=60t﹣t2.在飞机着陆滑行中,滑行最后的150m所用的时间是( )s.
A.10 B.20 C.30 D.10或30
2.长为,宽为的矩形,四个角上剪去边长为的小正方形,然后把四边折起来,作成底面为的无盖的长方体盒子,则y与x的关系式为( )
A. B.
C. D.
3.一台机器原价100万元,若每年的折旧率是x,两年后这台机器约为y万元,则y与x的函数关系式为( )
A. B. C. D.
4.一位运动员在距篮筐正下方水平距离处跳起投篮,球运行的路线是抛物线,当球运行的水平距离为时,达到最大高度,然后准确落入篮筐.如图所示,建立平面直角坐标系,已知篮筐中心到地面的距离为,该运动员身高,在这次跳投中,球在头顶上方处出手,球出手时,他跳离地面的高度是( )
A. B. C. D.
5.重装专卖店销售一种童装,若这种童装每天获利y(元)与销售单价x(元)满足关系,则要想获得最大利润每天必须卖出( )
A.25件 B.20件 C.30件 D.40件
6.某建筑物,从10m高的窗口A,用水管向外喷水,喷出的水呈抛物线状(抛物线所在的平面与墙面垂直),如图所示,如果抛物线的最高点M离墙1m,离地面m,则水流落地点B离墙的距离OB是( )
A.2m B.3m C.4m D.5m
7.如图,花坛水池中央有一喷泉,水管OP=3m,水从喷头P喷出后呈抛物线状先向上至最高点后落下,若最高点距水面4m,P距抛物线对称轴1m,则为使水不落到池外,水池半径最小为( )
A.1 B.1.5
C.2 D.3
8.设等边三角形的边长为x(x>0),面积为y,则y与x的函数关系式是( )
A.y=x2 B.y= C.y= D.y=
二、填空题
9.竖直上抛某物体时,物体离地面的高度h(m)与运动时间t(s)之间的关系可用公式来表示,由公式可知,该物体经过_____s离地面的高度为30m.
10.崇左市政府大楼前广场有一喷水池,水从地面喷出,喷出水的路径是一条抛物线.如果以水平地面为x轴,建立如图所示的平面直角坐标系,水在空中划出的曲线是抛物线y=﹣x2+4x(单位:米)的一部分.则水喷出的最大高度是___千米.
11.2013年5月26日,中国羽毛球队蝉联苏迪曼杯团体赛冠军,成就了首个五连冠霸业.比赛中羽毛球的某次运动路线可以看作是一条抛物线(如图).若不考虑外力因素,羽毛球行进高度y(米)与水平距离x(米)之间满足关系,则羽毛球飞出的水平距离为 米.
12.拱桥呈抛物线形,其函数关系式为,当拱桥下水位线在位置时,水面宽为,这时水面离桥拱顶端的高度是____________________.
13.周长为的矩形铁板上剪去一个等边三角形(这个等边三角形的一边是矩形的宽),则矩形宽为__________时,剩下的面积最大.
14.农机厂第一个月水泵的产量为50(台),第三个月的产量y(台)与月平均增长率x之间的关系表示为___________.
15.某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元,为了扩大销售,增加利润,尽快减少库存,商场决定采取适当的降价措施,经调查发现:如果每件村衫降价1元,商场平均每天可多售出2件.则商场降价后每天盈利y(元)与降价x(元)的函数关系式为____________________.
16.如图,在中,,,,动点从点开始沿边向以2的速度移动(不与点重合),动点从点开始沿边向以4的速度移动(不与点重合).如果、分别从、同时出发,那么经过______秒,四边形的面积最小.
三、解答题
17.某种产品现在的年产量是,计划今后两年增加产量.如果每年都比上一年的产量增加x倍,那么两年后这种产品的产量y将随计划所定的x的值而确定,y与x之间的关系应怎样表示?
18.竖直向上发射的物体的高度满足关系式,其中是物体运动的时间,是物体被发射时的速度.某公园计划设计园内喷泉,喷水的最大高度要求达到,那么喷水的速度应该达到多少?(结果精确到)
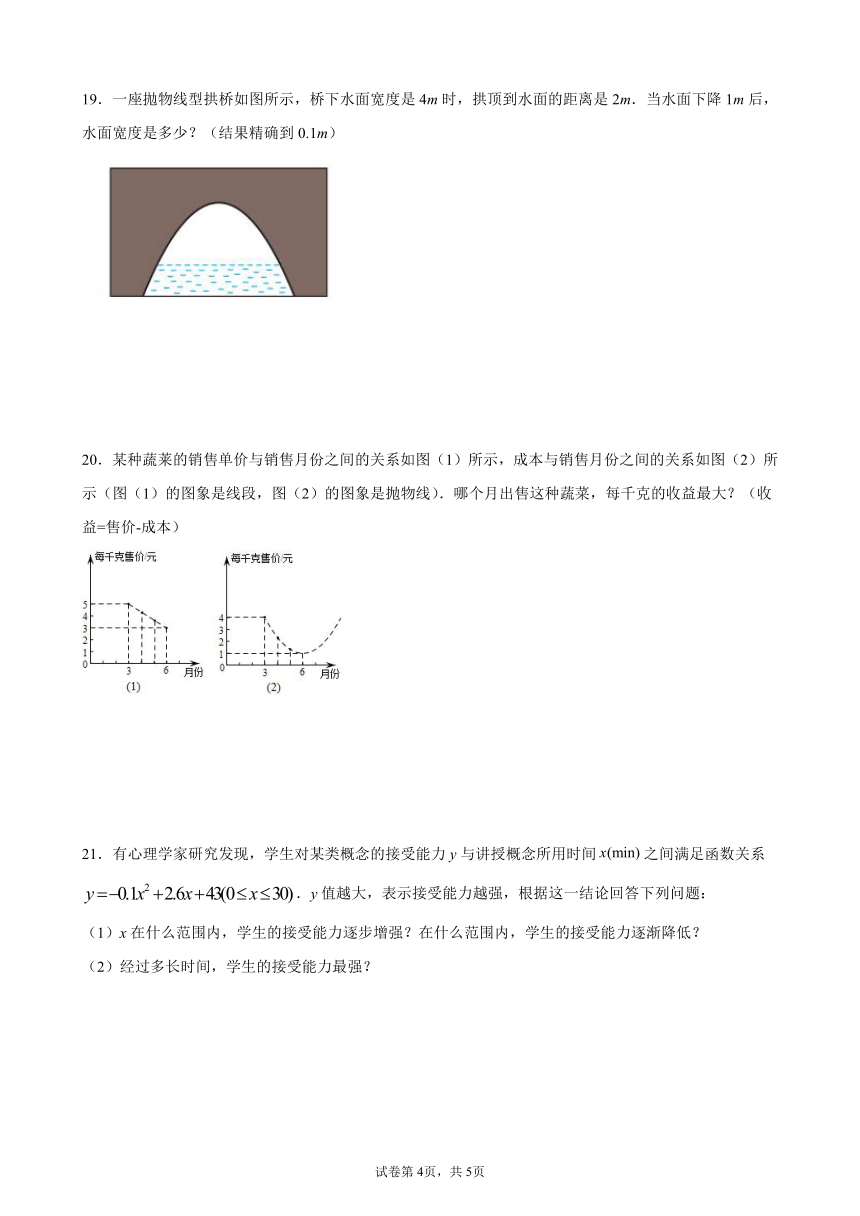
19.一座拋物线型拱桥如图所示,桥下水面宽度是4m时,拱顶到水面的距离是2m.当水面下降1m后,水面宽度是多少?(结果精确到0.1m)
20.某种蔬莱的销售单价与销售月份之间的关系如图(1)所示,成本与销售月份之间的关系如图(2)所示(图(1)的图象是线段,图(2)的图象是抛物线).哪个月出售这种蔬菜,每千克的收益最大?(收益=售价-成本)
21.有心理学家研究发现,学生对某类概念的接受能力y与讲授概念所用时间之间满足函数关系.y值越大,表示接受能力越强,根据这一结论回答下列问题:
(1)x在什么范围内,学生的接受能力逐步增强?在什么范围内,学生的接受能力逐渐降低?
(2)经过多长时间,学生的接受能力最强?
22.如图(单位:),等腰直角三角形以的速度沿直线l向正方形移动,直到与重合.设时,三角形与正方形重叠部分的面积为.
(1)写出y与x的关系式;
(2)当,3.5时,y分别是多少?
(3)当重叠部分的面积是正方形面积的一半时,三角形移动了多长时间?
23.一个足球被从地面向上踢出,它距地面的高度可以用公式来表示,其中表示足球被踢出后经过的时间.
(1)画出函数的图象;
(2)当时,足球距地面的高度分别是多少?
(3)方程的根的实际意义分别是什么?你能在图象上表示出来吗?
24.相框边的宽窄影响可放入相片的大小.如图,相框长,宽,相框边的宽,相框内的面积为.
(1)写出y与x的函数关系式;
(2)画出这个函数的图象;
(3)当,1.5,2时,分别可以放入多大的相片?
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.A
【解析】解:当y取得最大值时,飞机停下来,
则y=60t﹣1.5t2=﹣1.5(t﹣20)2+600,
此时t=20,飞机着陆后滑行600米才能停下来.
因此t的取值范围是0≤t≤20;
即当y=600﹣150=450时,
即60t﹣t2=450,
解得:t=10,t=30(不合题意舍去),
∴滑行最后的150m所用的时间是20﹣10=10,
故选:A.
2.C
【解析】解:设小正方形边长为xcm,由题意知:
现在底面长为(20-2x)cm,宽为(10-2x)cm,
则y=(10-2x)(20-2x)(0<x<5),
故选:C.
3.A
【解析】解:由题意得:二年后的价格是为:100×(1-x)×(1-x)=100(1-x)2,
则函数解析式是:y=100(1-x)2.
故选A.
4.A
【解析】∵当球运行的水平距离为时,达到最大高度,∴抛物线的顶点坐标为,∴设抛物线的解析式为.由题意知图象过点,∴,解得,抛物线的解析式为.设球出手时,他跳离地面的高度为.
∵抛物线的解析式为,球出手时,球的高度为.
∴,∴.
故选:A.
5.A
【解析】解:∵y=-x2+50x-500=-(x-25)2+125,
∴当x=25时,y取得最大值,最大值为125,
即销售单价为25元时,销售利润最大,
故选:A.
6.B
【解析】解:设抛物线的解析式为y=a(x﹣1)2+,
把点A(0,10)代入a(x﹣1)2+,得a(0﹣1)2+=10,
解得a=﹣,
因此抛物线解析式为y=﹣(x﹣1)2+,
当y=0时,解得x1=3,x2=﹣1(不合题意,舍去);
即OB=3米.
故选B.
7.D
【解析】如图建立坐标系:
抛物线的顶点坐标是(1,4),
设抛物线的解析式是y=a(x-1)2+4,
把(0,3)代入解析式得:a+4=3,
解得:a=-1,
则抛物线的解析式是:y=-(x-1)2+4,
当y=0时,-(x-1)2+4=0,
解得:x1=3,x2=-1(舍去),
则水池的最小半径是3米.
故选:D.
8.D
【解析】解:作出BC边上的高AD.
∵△ABC是等边三角形,边长为x,
∴CD=x,
∴高为h=x,
∴y=x×h=.
故选:D.
【点睛】
此题主要考查了三角形的面积的求法,找到等边三角形一边上的高是难点,求出三角形的高是解决问题的关键.
9.2或3
【解析】解:设该物体经过ts离地面的高度为30m
则整理得:
解得:t=2或3
10.4
【解析】∵水在空中划出的曲线是抛物线y=﹣x2+4x,
∴喷水的最大高度就是水在空中划出的抛物线y=﹣x2+4x的顶点坐标的纵坐标.
∵y=﹣x2+4x=﹣(x﹣2)2+4,∴顶点坐标为:(2,4).
∴喷水的最大高度为4千米.
11.5
【解析】当y=0时,,
解得:x1=﹣1(舍),x2=5.
∴羽毛球飞出的水平距离为5米.
12.
【解析】解:函数的顶点为(0,c),对称轴为x=0,
当水面宽为12m时,将x=6代入可得y=c-9,
此时水面离拱桥顶端的高度h是c-(c-9)=9m.
故答案为:9m.
13.
【解析】解:设矩形的宽为xcm,长为,
则剩下的面积=,
∴当时,面积有最大值,
故答案为:.
14.
【解析】第二个月是50(1+x),
第三个月是50(1+x)2
所以答案为y=50(1+x)2
15.
【解析】解:∵每件衬衫降价1元,商场平均每天可多售出2件,
∴每件衬衫降价x元,商场平均每天可多售出2x件,
∵原来每件的利润为40元,现在降价x元,
∴现在每件的利润为(40-x)元,
∴y=(40-x)(20+2x)=-2x2+60x+800.
故答案为:y=-2x2+60x+800.
16.3
【解析】解:设P、Q同时出发后经过的时间为ts,四边形APQC的面积为Scm2,则有:
S=S△ABC-S△PBQ=×12×6-(6-t)×2t
=t2-6t+36
=(t-3)2+27.
∴当t=3s时,S取得最小值.
故填:3.
17.,y是x的函数
【解析】解:这种产品的原产量是,一年后的产量是,再经过一年后的产量是,即两年后的产量,
即①
①式表示了两年后的产量y与计划增产的倍数x之间的关系,对于x的每一个值,y都有一个对应值,即y是x的函数.
18.喷水的速度应该达到17.32m/s.
【解析】解:h=-5t2+v0 t,其对称轴为t= .
当t=时,h最大=-5 ()2+v0 ==15,
整理得:v02=300,
∴v0=10≈17.32(m/s),或v0=-10(舍去),
答:喷水的速度应该达到17.32m/s.
19.水面宽度是4.9 m.
【解析】解:以水面所在的直线为x轴,以这座抛物线型拱桥的对称轴为y轴,建立平面直角坐标系,
设抛物线的函数关系式为:y=ax2+k,
∵抛物线过点(0,2),
∴有y=ax2+2,
又∵抛物线经过点(2,0),
∴有0=4a+2,
解得a=-,
∴y=-x2+2,
水面下降1m,即-1=-x2+2,
解得x=,或x=-(舍去),
∴水面宽度为2≈4.9.
∴当水面下降1m后,水面宽度是4.9 m.
20.5月出售这种蔬菜,每千克的收益最大
【解析】解:设y1=kx+b,将(3,5)和(6,3)代入得,
,
解得.
∴y1=-x+7.
由图象知抛物线的顶点坐标为(6,1),
设y2=a(x-6)2+1,把(3,4)代入得,
4=a(3-6)2+1,解得a=.
∴y2=(x-6)2+1,即y2=x2-4x+13;
∴收益W=y1-y2
=-x+7-(x2-4x+13)
=-(x-5)2+,
∵a=-<0,
∴当x=5时,W最大值=.
故5月出售这种蔬菜,每千克的收益最大,最大为元.
21.(1)当时,学生的接受能力逐渐增强;当时.学生的接受能力最强;当时,学生的接受能力逐渐降低;(2).
【解析】解:(1)y= 0.1+2.6x+43,
= 0.1+59.9
示意图如图:
当时,学生的接受能力逐渐增强;
当时.学生的接受能力最强;
当13<x≤30时,学生的接受能力逐步降低.
(2)顶点在坐标为(13,59.9),
∴当x=13时,y有最大值,
即经过13分钟时,学生的接受能力最强.
22.(1);(2)8,24.5;(3)当重叠部分的面积是正方形的一半时,三角形移动了5s.
【解析】解:(1)因为三角形与正方形重合部分是个等腰直角三角形,且直角边都是2x,
所以y=×2x×2x=2x2;
(2)在y=2x2中,
当x=2时,y=8;
当x=3.5时,y=24.5;
(3)在y=2x2中,
因为当y=50时,2x2=50,
所以x2=25,
解得x=5s(负值舍去).
即当重叠部分的面积是正方形的一半时,三角形移动了5s.
23.(1)见解析;(2);(3)球离开地面及落地的时间,足球高度是时的时间.图象见解析
【解析】解:(1)画出函数h=﹣4.9t2+19.6t的图象如图所示;
(2)把t=1,t=2分别代入h=﹣4.9t2+19.6t得,
h=﹣4.9+19.6=14.7,h=﹣4.9×22+19.6×2=19.6,
故当t=1,t=2时,足球距地面的高度分别是14.7和19.6;
(3)解﹣4.9t2+19.6t=0,得t1=0,t2=4,
其中t1=0表示足球离开地面的时间,t2=4表示足球落地的时间;
解﹣4.9t2+19.6t=14.7得,t3=1,t4=3,
其中t3=1表示足球离开地面的高度是14.7m时的时间,t2=4离开地面的高度是14.7m时的时间,
24.(1);(2)见解析;(3),,
【解析】(1)相框长,宽,相框边的宽,相框内的面积为.
由题意得,
(2)列表:
x 0 1 2 3 4 5 6 7
y 572 480 396 320 252 192 140 96
描点,连线,如图,
(3)当时,,,则相片尺寸为,
当时,,,则相片尺寸为,
当时,,,则相片尺寸为.
答案第1页,共2页
答案第1页,共2页
22.3实际问题与二次函数-同步练习
时间:60分钟
一、单选题
1.飞机着陆后滑行的距离y(单位:m)关于滑行时间以(单位:)的函数解析式是y=60t﹣t2.在飞机着陆滑行中,滑行最后的150m所用的时间是( )s.
A.10 B.20 C.30 D.10或30
2.长为,宽为的矩形,四个角上剪去边长为的小正方形,然后把四边折起来,作成底面为的无盖的长方体盒子,则y与x的关系式为( )
A. B.
C. D.
3.一台机器原价100万元,若每年的折旧率是x,两年后这台机器约为y万元,则y与x的函数关系式为( )
A. B. C. D.
4.一位运动员在距篮筐正下方水平距离处跳起投篮,球运行的路线是抛物线,当球运行的水平距离为时,达到最大高度,然后准确落入篮筐.如图所示,建立平面直角坐标系,已知篮筐中心到地面的距离为,该运动员身高,在这次跳投中,球在头顶上方处出手,球出手时,他跳离地面的高度是( )
A. B. C. D.
5.重装专卖店销售一种童装,若这种童装每天获利y(元)与销售单价x(元)满足关系,则要想获得最大利润每天必须卖出( )
A.25件 B.20件 C.30件 D.40件
6.某建筑物,从10m高的窗口A,用水管向外喷水,喷出的水呈抛物线状(抛物线所在的平面与墙面垂直),如图所示,如果抛物线的最高点M离墙1m,离地面m,则水流落地点B离墙的距离OB是( )
A.2m B.3m C.4m D.5m
7.如图,花坛水池中央有一喷泉,水管OP=3m,水从喷头P喷出后呈抛物线状先向上至最高点后落下,若最高点距水面4m,P距抛物线对称轴1m,则为使水不落到池外,水池半径最小为( )
A.1 B.1.5
C.2 D.3
8.设等边三角形的边长为x(x>0),面积为y,则y与x的函数关系式是( )
A.y=x2 B.y= C.y= D.y=
二、填空题
9.竖直上抛某物体时,物体离地面的高度h(m)与运动时间t(s)之间的关系可用公式来表示,由公式可知,该物体经过_____s离地面的高度为30m.
10.崇左市政府大楼前广场有一喷水池,水从地面喷出,喷出水的路径是一条抛物线.如果以水平地面为x轴,建立如图所示的平面直角坐标系,水在空中划出的曲线是抛物线y=﹣x2+4x(单位:米)的一部分.则水喷出的最大高度是___千米.
11.2013年5月26日,中国羽毛球队蝉联苏迪曼杯团体赛冠军,成就了首个五连冠霸业.比赛中羽毛球的某次运动路线可以看作是一条抛物线(如图).若不考虑外力因素,羽毛球行进高度y(米)与水平距离x(米)之间满足关系,则羽毛球飞出的水平距离为 米.
12.拱桥呈抛物线形,其函数关系式为,当拱桥下水位线在位置时,水面宽为,这时水面离桥拱顶端的高度是____________________.
13.周长为的矩形铁板上剪去一个等边三角形(这个等边三角形的一边是矩形的宽),则矩形宽为__________时,剩下的面积最大.
14.农机厂第一个月水泵的产量为50(台),第三个月的产量y(台)与月平均增长率x之间的关系表示为___________.
15.某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元,为了扩大销售,增加利润,尽快减少库存,商场决定采取适当的降价措施,经调查发现:如果每件村衫降价1元,商场平均每天可多售出2件.则商场降价后每天盈利y(元)与降价x(元)的函数关系式为____________________.
16.如图,在中,,,,动点从点开始沿边向以2的速度移动(不与点重合),动点从点开始沿边向以4的速度移动(不与点重合).如果、分别从、同时出发,那么经过______秒,四边形的面积最小.
三、解答题
17.某种产品现在的年产量是,计划今后两年增加产量.如果每年都比上一年的产量增加x倍,那么两年后这种产品的产量y将随计划所定的x的值而确定,y与x之间的关系应怎样表示?
18.竖直向上发射的物体的高度满足关系式,其中是物体运动的时间,是物体被发射时的速度.某公园计划设计园内喷泉,喷水的最大高度要求达到,那么喷水的速度应该达到多少?(结果精确到)
19.一座拋物线型拱桥如图所示,桥下水面宽度是4m时,拱顶到水面的距离是2m.当水面下降1m后,水面宽度是多少?(结果精确到0.1m)
20.某种蔬莱的销售单价与销售月份之间的关系如图(1)所示,成本与销售月份之间的关系如图(2)所示(图(1)的图象是线段,图(2)的图象是抛物线).哪个月出售这种蔬菜,每千克的收益最大?(收益=售价-成本)
21.有心理学家研究发现,学生对某类概念的接受能力y与讲授概念所用时间之间满足函数关系.y值越大,表示接受能力越强,根据这一结论回答下列问题:
(1)x在什么范围内,学生的接受能力逐步增强?在什么范围内,学生的接受能力逐渐降低?
(2)经过多长时间,学生的接受能力最强?
22.如图(单位:),等腰直角三角形以的速度沿直线l向正方形移动,直到与重合.设时,三角形与正方形重叠部分的面积为.
(1)写出y与x的关系式;
(2)当,3.5时,y分别是多少?
(3)当重叠部分的面积是正方形面积的一半时,三角形移动了多长时间?
23.一个足球被从地面向上踢出,它距地面的高度可以用公式来表示,其中表示足球被踢出后经过的时间.
(1)画出函数的图象;
(2)当时,足球距地面的高度分别是多少?
(3)方程的根的实际意义分别是什么?你能在图象上表示出来吗?
24.相框边的宽窄影响可放入相片的大小.如图,相框长,宽,相框边的宽,相框内的面积为.
(1)写出y与x的函数关系式;
(2)画出这个函数的图象;
(3)当,1.5,2时,分别可以放入多大的相片?
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.A
【解析】解:当y取得最大值时,飞机停下来,
则y=60t﹣1.5t2=﹣1.5(t﹣20)2+600,
此时t=20,飞机着陆后滑行600米才能停下来.
因此t的取值范围是0≤t≤20;
即当y=600﹣150=450时,
即60t﹣t2=450,
解得:t=10,t=30(不合题意舍去),
∴滑行最后的150m所用的时间是20﹣10=10,
故选:A.
2.C
【解析】解:设小正方形边长为xcm,由题意知:
现在底面长为(20-2x)cm,宽为(10-2x)cm,
则y=(10-2x)(20-2x)(0<x<5),
故选:C.
3.A
【解析】解:由题意得:二年后的价格是为:100×(1-x)×(1-x)=100(1-x)2,
则函数解析式是:y=100(1-x)2.
故选A.
4.A
【解析】∵当球运行的水平距离为时,达到最大高度,∴抛物线的顶点坐标为,∴设抛物线的解析式为.由题意知图象过点,∴,解得,抛物线的解析式为.设球出手时,他跳离地面的高度为.
∵抛物线的解析式为,球出手时,球的高度为.
∴,∴.
故选:A.
5.A
【解析】解:∵y=-x2+50x-500=-(x-25)2+125,
∴当x=25时,y取得最大值,最大值为125,
即销售单价为25元时,销售利润最大,
故选:A.
6.B
【解析】解:设抛物线的解析式为y=a(x﹣1)2+,
把点A(0,10)代入a(x﹣1)2+,得a(0﹣1)2+=10,
解得a=﹣,
因此抛物线解析式为y=﹣(x﹣1)2+,
当y=0时,解得x1=3,x2=﹣1(不合题意,舍去);
即OB=3米.
故选B.
7.D
【解析】如图建立坐标系:
抛物线的顶点坐标是(1,4),
设抛物线的解析式是y=a(x-1)2+4,
把(0,3)代入解析式得:a+4=3,
解得:a=-1,
则抛物线的解析式是:y=-(x-1)2+4,
当y=0时,-(x-1)2+4=0,
解得:x1=3,x2=-1(舍去),
则水池的最小半径是3米.
故选:D.
8.D
【解析】解:作出BC边上的高AD.
∵△ABC是等边三角形,边长为x,
∴CD=x,
∴高为h=x,
∴y=x×h=.
故选:D.
【点睛】
此题主要考查了三角形的面积的求法,找到等边三角形一边上的高是难点,求出三角形的高是解决问题的关键.
9.2或3
【解析】解:设该物体经过ts离地面的高度为30m
则整理得:
解得:t=2或3
10.4
【解析】∵水在空中划出的曲线是抛物线y=﹣x2+4x,
∴喷水的最大高度就是水在空中划出的抛物线y=﹣x2+4x的顶点坐标的纵坐标.
∵y=﹣x2+4x=﹣(x﹣2)2+4,∴顶点坐标为:(2,4).
∴喷水的最大高度为4千米.
11.5
【解析】当y=0时,,
解得:x1=﹣1(舍),x2=5.
∴羽毛球飞出的水平距离为5米.
12.
【解析】解:函数的顶点为(0,c),对称轴为x=0,
当水面宽为12m时,将x=6代入可得y=c-9,
此时水面离拱桥顶端的高度h是c-(c-9)=9m.
故答案为:9m.
13.
【解析】解:设矩形的宽为xcm,长为,
则剩下的面积=,
∴当时,面积有最大值,
故答案为:.
14.
【解析】第二个月是50(1+x),
第三个月是50(1+x)2
所以答案为y=50(1+x)2
15.
【解析】解:∵每件衬衫降价1元,商场平均每天可多售出2件,
∴每件衬衫降价x元,商场平均每天可多售出2x件,
∵原来每件的利润为40元,现在降价x元,
∴现在每件的利润为(40-x)元,
∴y=(40-x)(20+2x)=-2x2+60x+800.
故答案为:y=-2x2+60x+800.
16.3
【解析】解:设P、Q同时出发后经过的时间为ts,四边形APQC的面积为Scm2,则有:
S=S△ABC-S△PBQ=×12×6-(6-t)×2t
=t2-6t+36
=(t-3)2+27.
∴当t=3s时,S取得最小值.
故填:3.
17.,y是x的函数
【解析】解:这种产品的原产量是,一年后的产量是,再经过一年后的产量是,即两年后的产量,
即①
①式表示了两年后的产量y与计划增产的倍数x之间的关系,对于x的每一个值,y都有一个对应值,即y是x的函数.
18.喷水的速度应该达到17.32m/s.
【解析】解:h=-5t2+v0 t,其对称轴为t= .
当t=时,h最大=-5 ()2+v0 ==15,
整理得:v02=300,
∴v0=10≈17.32(m/s),或v0=-10(舍去),
答:喷水的速度应该达到17.32m/s.
19.水面宽度是4.9 m.
【解析】解:以水面所在的直线为x轴,以这座抛物线型拱桥的对称轴为y轴,建立平面直角坐标系,
设抛物线的函数关系式为:y=ax2+k,
∵抛物线过点(0,2),
∴有y=ax2+2,
又∵抛物线经过点(2,0),
∴有0=4a+2,
解得a=-,
∴y=-x2+2,
水面下降1m,即-1=-x2+2,
解得x=,或x=-(舍去),
∴水面宽度为2≈4.9.
∴当水面下降1m后,水面宽度是4.9 m.
20.5月出售这种蔬菜,每千克的收益最大
【解析】解:设y1=kx+b,将(3,5)和(6,3)代入得,
,
解得.
∴y1=-x+7.
由图象知抛物线的顶点坐标为(6,1),
设y2=a(x-6)2+1,把(3,4)代入得,
4=a(3-6)2+1,解得a=.
∴y2=(x-6)2+1,即y2=x2-4x+13;
∴收益W=y1-y2
=-x+7-(x2-4x+13)
=-(x-5)2+,
∵a=-<0,
∴当x=5时,W最大值=.
故5月出售这种蔬菜,每千克的收益最大,最大为元.
21.(1)当时,学生的接受能力逐渐增强;当时.学生的接受能力最强;当时,学生的接受能力逐渐降低;(2).
【解析】解:(1)y= 0.1+2.6x+43,
= 0.1+59.9
示意图如图:
当时,学生的接受能力逐渐增强;
当时.学生的接受能力最强;
当13<x≤30时,学生的接受能力逐步降低.
(2)顶点在坐标为(13,59.9),
∴当x=13时,y有最大值,
即经过13分钟时,学生的接受能力最强.
22.(1);(2)8,24.5;(3)当重叠部分的面积是正方形的一半时,三角形移动了5s.
【解析】解:(1)因为三角形与正方形重合部分是个等腰直角三角形,且直角边都是2x,
所以y=×2x×2x=2x2;
(2)在y=2x2中,
当x=2时,y=8;
当x=3.5时,y=24.5;
(3)在y=2x2中,
因为当y=50时,2x2=50,
所以x2=25,
解得x=5s(负值舍去).
即当重叠部分的面积是正方形的一半时,三角形移动了5s.
23.(1)见解析;(2);(3)球离开地面及落地的时间,足球高度是时的时间.图象见解析
【解析】解:(1)画出函数h=﹣4.9t2+19.6t的图象如图所示;
(2)把t=1,t=2分别代入h=﹣4.9t2+19.6t得,
h=﹣4.9+19.6=14.7,h=﹣4.9×22+19.6×2=19.6,
故当t=1,t=2时,足球距地面的高度分别是14.7和19.6;
(3)解﹣4.9t2+19.6t=0,得t1=0,t2=4,
其中t1=0表示足球离开地面的时间,t2=4表示足球落地的时间;
解﹣4.9t2+19.6t=14.7得,t3=1,t4=3,
其中t3=1表示足球离开地面的高度是14.7m时的时间,t2=4离开地面的高度是14.7m时的时间,
24.(1);(2)见解析;(3),,
【解析】(1)相框长,宽,相框边的宽,相框内的面积为.
由题意得,
(2)列表:
x 0 1 2 3 4 5 6 7
y 572 480 396 320 252 192 140 96
描点,连线,如图,
(3)当时,,,则相片尺寸为,
当时,,,则相片尺寸为,
当时,,,则相片尺寸为.
答案第1页,共2页
答案第1页,共2页
同课章节目录
