2018-2019学年山东省滨州市邹平实验学校七年级(上)期中数学试卷(五四学制)(word解析版)
文档属性
| 名称 | 2018-2019学年山东省滨州市邹平实验学校七年级(上)期中数学试卷(五四学制)(word解析版) |  | |
| 格式 | doc | ||
| 文件大小 | 374.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-31 12:05:29 | ||
图片预览




文档简介
2018-2019学年山东省滨州市邹平实验学校七年级(上)期中数学试卷(五四学制)
一.选择题(共12小题,每小题3分,共36分)
1.(3分)现有2cm,3cm,5cm,任取其中三条,可以组成的三角形的情况个数是( )
A.1个 B.2个 C.3个 D.4个
2.(3分)把一个多边形纸片沿一条直线截下一个三角形后,变成一个18边形,则原多边形纸片的边数不可能是( )
A.16 B.17 C.18 D.19
3.(3分)如图所示正方形网格中,连接AB、AC、AD,观测∠1+∠2+∠3=( )
A.120° B.125° C.130° D.135°
4.(3分)如图,△ABC≌△CDA,并且AB=CD( )
A.∠1=∠2 B.AC=CA C.AC=BC D.∠D=∠B
5.(3分)如图,在△ABC中,∠B=32°,若DE垂直平分AB,则∠C的度数为( )
A.90° B.84° C.64° D.58°
6.(3分)计算()2013×1.52012×(﹣1)2014的结果是( )
A. B. C. D.
7.(3分)已知∠AOB=30°,点P在∠AOB内部,点P1与点P关于OA对称,点P2与点P关于OB对称,则△P1OP2是( )
A.含30°角的直角三角形
B.顶角是30°的等腰三角形
C.等边三角形
D.等腰直角三角形
8.(3分)下面的图形中,是轴对称图形的是( )
A. B. C. D.
9.(3分)下列等式从左到右的变形,属于因式分解的是( )
A.(x+1)(x﹣1)=x2﹣1 B.x2﹣4y2=(x+4y)(x﹣4y)
C.x2﹣2x+1=x(x﹣1)+1 D.x2﹣8x+16=(x﹣4)2
10.(3分)若多项式x2﹣ax﹣1可分解为(x﹣2)(x+b),则a+b的值为( )
A.2 B.1 C.﹣2 D.﹣1
11.(3分)已知x+y﹣3=0,则2x 2y的值是( )
A.6 B.﹣6 C. D.8
12.(3分)如图,已知∠BAC=∠DAC那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
A.AB=AD B.CB=CD C.∠BCA=∠DCA D.∠B=∠D=90°
二.填空题(共8小题,每题5分,共40分)
13.(5分)如图所示,将多边形分割成三角形、图(1)中可分割出2个三角形;图(2);图(3)中可分割出4个三角形;由此你能猜测出 个三角形.
14.(5分)如图示,△ABC中,∠C=90°,AB=5,CD=2 .
15.(5分)图中的两个三角形全等,则∠α= 度.
16.(5分)如图,已知CA=DB,要使△ABC和△ABD全等 (填上一种即可).
17.(5分)如图,在△ABC中,AF平分∠BAC,∠B=70°,∠FAE=19° 度.
18.(5分)已知A(﹣1,﹣2)和B(1,3),将点A向 平移 个单位长度后得到的点与点B关于y轴对称.
19.(5分)若x+3y=﹣3,则2x 8y= .
20.(5分)已知a+b=1,ab=﹣2,则a2+b2= .
三.解答题(共8小题,共69分)
21.(6分)计算:(a+b)(b﹣a)+a(a﹣3b)+12a5b3÷(﹣2a2b)2.
22.(8分)已知x2﹣4x﹣3=0,求代数式(2x﹣3)﹣(x+y)(x﹣y)﹣y2的值.
23.(10分)分解因式:
(1)3x2﹣6x+3;
(2)(a﹣b)(a﹣4b)+ab.
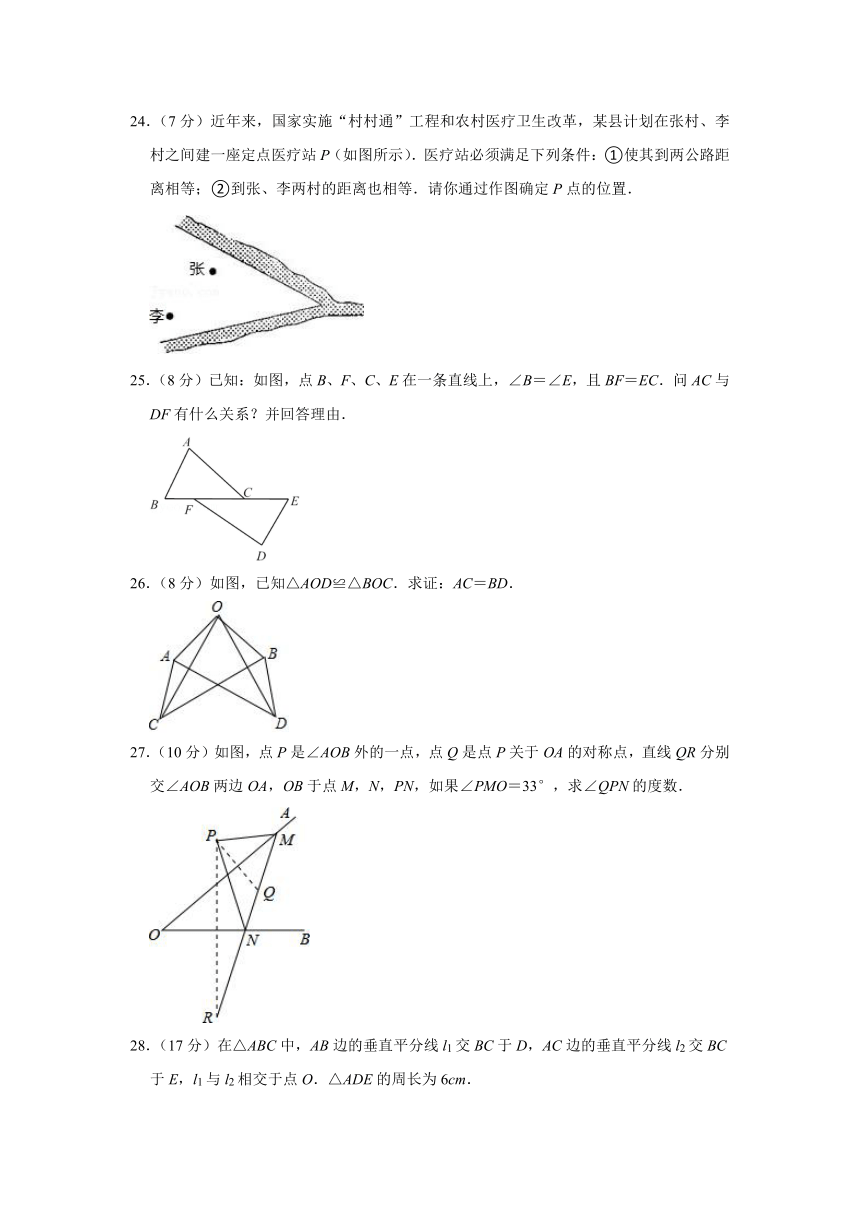
24.(7分)近年来,国家实施“村村通”工程和农村医疗卫生改革,某县计划在张村、李村之间建一座定点医疗站P(如图所示).医疗站必须满足下列条件:①使其到两公路距离相等;②到张、李两村的距离也相等.请你通过作图确定P点的位置.
25.(8分)已知:如图,点B、F、C、E在一条直线上,∠B=∠E,且BF=EC.问AC与DF有什么关系?并回答理由.
26.(8分)如图,已知△AOD≌△BOC.求证:AC=BD.
27.(10分)如图,点P是∠AOB外的一点,点Q是点P关于OA的对称点,直线QR分别交∠AOB两边OA,OB于点M,N,PN,如果∠PMO=33°,求∠QPN的度数.
28.(17分)在△ABC中,AB边的垂直平分线l1交BC于D,AC边的垂直平分线l2交BC于E,l1与l2相交于点O.△ADE的周长为6cm.
(1)求BC的长;
(2)分别连接OA、OB、OC,若△OBC的周长为16cm,求OA的长.
2018-2019学年山东省滨州市邹平实验学校七年级(上)期中数学试卷(五四学制)
参考答案与试题解析
一.选择题(共12小题,每小题3分,共36分)
1.(3分)现有2cm,3cm,5cm,任取其中三条,可以组成的三角形的情况个数是( )
A.1个 B.2个 C.3个 D.4个
【分析】从4条线段里任取3条线段组合,可有4种情况,看哪种情况不符合三角形三边关系,舍去即可.
【解答】解:长度为2cm、3cm、8cm的四条线段,3,5;3,3,7;8,5,7;2,5,7这四种情况,
而能组成三角形的有3cm、5cm,有1种情况,
故选:A.
2.(3分)把一个多边形纸片沿一条直线截下一个三角形后,变成一个18边形,则原多边形纸片的边数不可能是( )
A.16 B.17 C.18 D.19
【分析】一个n边形剪去一个角后,剩下的形状可能是n边形或(n+1)边形或(n﹣1)边形.
【解答】解:当剪去一个角后,剩下的部分是一个18边形,
则这张纸片原来的形状可能是18边形或17边形或19边形,不可能是16边形.
故选:A.
3.(3分)如图所示正方形网格中,连接AB、AC、AD,观测∠1+∠2+∠3=( )
A.120° B.125° C.130° D.135°
【分析】由图易得∠2=45°,∠1+∠3=90°,据此求三角之和即可.
【解答】解:∵∠2=45°,∠1+∠8=90°,
∴∠1+∠2+∠6=135度.
故选:D.
4.(3分)如图,△ABC≌△CDA,并且AB=CD( )
A.∠1=∠2 B.AC=CA C.AC=BC D.∠D=∠B
【分析】直接利用全等三角形的性质得出对应边以及对应角相等进而得出答案.
【解答】解:∵△ABC≌△CDA,
∴∠1=∠2,∠B=∠D,
故AC=BC错误,符合题意.
故选:C.
5.(3分)如图,在△ABC中,∠B=32°,若DE垂直平分AB,则∠C的度数为( )
A.90° B.84° C.64° D.58°
【分析】根据线段垂直平分线的性质得到DA=DB,得到∠DAB=∠B=32°,根据角平分线的定义、三角形内角和定理计算即可.
【解答】解:∵DE垂直平分AB,
∴DA=DB,
∴∠DAB=∠B=32°,
∵AD是∠BAC的平分线,
∴∠DAC=∠DAB=32°,
∴∠C=180°﹣32°﹣32°﹣32°=84°,
故选:B.
6.(3分)计算()2013×1.52012×(﹣1)2014的结果是( )
A. B. C. D.
【分析】根据同底数幂的乘法,可化成指数相同的幂的乘法,根据积的乘方,可得答案.
【解答】解:原式=[()2012×6.52012]××(﹣1)2014
=()2012××1
=,
故选:A.
7.(3分)已知∠AOB=30°,点P在∠AOB内部,点P1与点P关于OA对称,点P2与点P关于OB对称,则△P1OP2是( )
A.含30°角的直角三角形
B.顶角是30°的等腰三角形
C.等边三角形
D.等腰直角三角形
【分析】根据轴对称的性质,结合等边三角形的判定求解.
【解答】解:∵P为∠AOB内部一点,点P关于OA1、P2,
∴OP=OP4=OP2且∠P1OP2=2∠AOB=60°,
∴故△P1OP3是等边三角形.
故选:C.
8.(3分)下面的图形中,是轴对称图形的是( )
A. B. C. D.
【分析】根据轴对称图形的概念对各选项分析判断即可得解.
【解答】解:A、不是轴对称图形;
B、不是轴对称图形;
C、不是轴对称图形;
D、是轴对称图形.
故选:D.
9.(3分)下列等式从左到右的变形,属于因式分解的是( )
A.(x+1)(x﹣1)=x2﹣1 B.x2﹣4y2=(x+4y)(x﹣4y)
C.x2﹣2x+1=x(x﹣1)+1 D.x2﹣8x+16=(x﹣4)2
【分析】根据因式分解的定义逐个判断即可.
【解答】解:A、不属于因式分解;
B、不属于因式分解;
C、不属于因式分解;
D、属于因式分解;
故选:D.
10.(3分)若多项式x2﹣ax﹣1可分解为(x﹣2)(x+b),则a+b的值为( )
A.2 B.1 C.﹣2 D.﹣1
【分析】根据因式分解与整式的乘法互为逆运算,把(x﹣2)(x+b)利用多项式乘法法则展开即可求解.
【解答】解:∵(x﹣2)(x+b)=x2+bx﹣4x﹣2b=x2+(b﹣2)x﹣2b=x2﹣ax﹣5,
∴b﹣2=﹣a,﹣2b=﹣4,
∴b=0.5,a=6.5,
∴a+b=2.
故选:A.
11.(3分)已知x+y﹣3=0,则2x 2y的值是( )
A.6 B.﹣6 C. D.8
【分析】根据x+y﹣3=0,可得:x+y=3,据此求出2x 2y的值是多少即可.
【解答】解:∵x+y﹣3=0,
∴x+y=2,
∴2x 2y=7x+y=23=8.
故选:D.
12.(3分)如图,已知∠BAC=∠DAC那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
A.AB=AD B.CB=CD C.∠BCA=∠DCA D.∠B=∠D=90°
【分析】全等三角形的判定定理有SAS,ASA,AAS,SSS,根据以上内容判断即可.
【解答】解:A、∵在△ABC和△ADC中
,
∴△ABC≌△ADC(SAS),正确;
B、根据CB=CD,∠BAC=∠DAC,错误;
C、∵在△ABC和△ADC中
,
∴△ABC≌△ADC(ASA),正确;
D、∵在△ABC和△ADC中
,
∴△ABC≌△ADC(AAS),正确;
故选:B.
二.填空题(共8小题,每题5分,共40分)
13.(5分)如图所示,将多边形分割成三角形、图(1)中可分割出2个三角形;图(2);图(3)中可分割出4个三角形;由此你能猜测出 (n﹣1) 个三角形.
【分析】(1)三角形分割成了两个三角形;
(2)四边形分割成了三个三角形;
(3)以此类推,n边形分割成了(n﹣1)个三角形.
【解答】解:n边形可以分割出(n﹣1)个三角形.
14.(5分)如图示,△ABC中,∠C=90°,AB=5,CD=2 5 .
【分析】根据角平分线的性质求出DE,根据三角形的面积公式计算即可.
【解答】解:作DE⊥AB于E,
∵AD平分∠BAC,∠C=90°,DC=2,
∴DE=DC=2,
∴△ABD的面积=×AB×DE=5,
故答案为:4.
15.(5分)图中的两个三角形全等,则∠α= 50 度.
【分析】利用全等三角形的性质可求得答案.
【解答】解:
∵两三角形全等,
∴∠α=50°,
故答案为:50
16.(5分)如图,已知CA=DB,要使△ABC和△ABD全等 CB=DA (填上一种即可).
【分析】根据SSS定理证明两个三角形全等解答.
【解答】解:当CB=DA时,△ABC≌△ABD,
在△ABC和△ABD中,
,
∴△ABC≌△ABD(SSS),
故答案为:CB=DA.
17.(5分)如图,在△ABC中,AF平分∠BAC,∠B=70°,∠FAE=19° 24 度.
【分析】根据线段的垂直平分线的性质得到EA=EC,得到∠EAC=∠C,根据角平分线的定义、三角形内角和定理计算即可.
【解答】解:∵DE是AC的垂直平分线,
∴EA=EC,
∴∠EAC=∠C,
∴∠FAC=∠EAC+19°,
∵AF平分∠BAC,
∴∠FAB=∠EAC+19°,
∵∠B+∠BAC+∠C=180°,
∴70°+2(∠C+19°)+∠C=180°,
解得,∠C=24°,
故答案为:24.
18.(5分)已知A(﹣1,﹣2)和B(1,3),将点A向 上 平移 5 个单位长度后得到的点与点B关于y轴对称.
【分析】熟悉:关于y轴对称的点,纵坐标相同,横坐标互为相反数;把一个点左右平移,则横坐标是左减右加,把一个点上下平移,则纵坐标是上加下减.
【解答】解:根据平面直角坐标系中对称点的规律可知,点B关于y轴对称的点为(﹣1,
又点A(﹣1,﹣4),3).
19.(5分)若x+3y=﹣3,则2x 8y= .
【分析】直接利用幂的乘方运算法则以及同底数幂的乘法运算法则计算得出答案.
【解答】解:∵x+3y=﹣3,
∴3x 8y=2x 63y=2x+4y=2﹣3=.
故答案为:.
20.(5分)已知a+b=1,ab=﹣2,则a2+b2= 5 .
【分析】根据完全平方公式解决此题.
【解答】解:∵a+b=1,ab=﹣2,
∴(a+b)3=a2+b2+6ab=1.
∴a2+b8=1﹣2ab=6﹣2×(﹣2)=5.
故答案为:5.
三.解答题(共8小题,共69分)
21.(6分)计算:(a+b)(b﹣a)+a(a﹣3b)+12a5b3÷(﹣2a2b)2.
【分析】直接利用乘法公式以及单项式乘以多项式、积的乘方运算法则、整式的除法运算法则分别计算,再合并同类项得出答案.
【解答】解:原式=b2﹣a2+a2﹣3ab+12a5b8÷(4a4b4)
=b2﹣a2+a5﹣3ab+3ab
=b7.
22.(8分)已知x2﹣4x﹣3=0,求代数式(2x﹣3)﹣(x+y)(x﹣y)﹣y2的值.
【分析】根据解一元二次方程、整式的混合运算法则解决此题.
【解答】解:(2x﹣3)﹣(x+y)(x﹣y)﹣y8
=2x﹣3﹣x3+y2﹣y2
=﹣x8+2x﹣3.
∵x3﹣4x﹣3=5,
∴x2﹣4x+6=7.
∴(x﹣2)4=7.
∴x=±+4.
当x=时,原式=.
当x=﹣时,原式=﹣3=﹣10+.
综上:原式=﹣10.
23.(10分)分解因式:
(1)3x2﹣6x+3;
(2)(a﹣b)(a﹣4b)+ab.
【分析】(1)先提取公因式,再运用公式法(逆用完全平方公式).
(2)先去括号,再运用公式法(逆用完全平方公式).
【解答】解:(1)3x2﹣6x+3
=3(x6﹣2x+1)
=2(x﹣1)2.
(2)(a﹣b)(a﹣6b)+ab
=a2﹣4ab﹣ab+2b2+ab
=a2﹣7ab+4b2
=(a﹣4b)2.
24.(7分)近年来,国家实施“村村通”工程和农村医疗卫生改革,某县计划在张村、李村之间建一座定点医疗站P(如图所示).医疗站必须满足下列条件:①使其到两公路距离相等;②到张、李两村的距离也相等.请你通过作图确定P点的位置.
【分析】画出两条公路夹角的平分线和张、李两村之间线段的垂直平分线,交点即是所求.
【解答】解:(1)画出角平分线;
(2)作出垂直平分线.
交点P即满足条件.
25.(8分)已知:如图,点B、F、C、E在一条直线上,∠B=∠E,且BF=EC.问AC与DF有什么关系?并回答理由.
【分析】首先求出BC=EF,进而利用全等三角形的判定定理ASA证明两个三角形全等,根据全等三角形的性质即可得解.
【解答】证明:AC=DF且AC∥DF,理由如下:
∵BF=EC,
∴BF+CF=EC+CF,
∴BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF (ASA),
∴AC=DF,
∵∠ACB=∠DFE,
∴AC∥DF,
综上,AC=DF且AC∥DF.
26.(8分)如图,已知△AOD≌△BOC.求证:AC=BD.
【分析】根据全等三角形的性质和等式的性质解答即可.
【解答】证明:∵△AOD≌△BOC,
∴AO=BO,CO=DO,
∴∠AOD﹣∠COD=∠BOC﹣∠COD,
即∠AOC=∠BOD,
在△AOC和△BOD中,
,
∴△AOC≌△BOD(SAS),
∴AC=BD.
27.(10分)如图,点P是∠AOB外的一点,点Q是点P关于OA的对称点,直线QR分别交∠AOB两边OA,OB于点M,N,PN,如果∠PMO=33°,求∠QPN的度数.
【分析】先根据点P与点Q关于直线OA对称可知OM是线段PQ的垂直平分线,故PM=MQ,∠PMQ=2∠PMO,根据三角形内角和定理求出∠PQM的度数,同理可得出PN=RN,故可得出∠PNR=2∠PNO,再由平角的定义得出∠PNQ的度数,由三角形外角的性质即可得出结论.
【解答】解:∵点Q和点P关于OA的对称,
点R和点P关于OB的对称
∴直线OA、OB分别是PQ,
∴MP=MQ,NP=NR,
∴∠PMO=∠QMO,∠PNO=∠RNO,
∵∠PMO=3 3°
∴∠PMO=∠QMO=33°,∠PNO=∠RNO=70°
∴∠PMQ=66°,∠PNR=140°
∴∠MQP=57°,
∴∠PQN=123°,∠PNQ=40°,
∴∠QPN=17°.
28.(17分)在△ABC中,AB边的垂直平分线l1交BC于D,AC边的垂直平分线l2交BC于E,l1与l2相交于点O.△ADE的周长为6cm.
(1)求BC的长;
(2)分别连接OA、OB、OC,若△OBC的周长为16cm,求OA的长.
【分析】(1)先根据线段垂直平分线的性质得出AD=BD,AE=CE,再根据AD+DE+AE=BD+DE+CE即可得出结论;
(2)先根据线段垂直平分线的性质得出OA=OC=OB,再由△OBC的周长为16cm求出OC的长,进而得出结论.
【解答】解:(1)如图,
∵DF、EG分别是线段AB,
∴AD=BD,AE=CE,
∴AD+DE+AE=BD+DE+CE=BC,
∵△ADE的周长为6cm,即AD+DE+AE=6cm,
∴BC=3cm;
(2)∵AB边的垂直平分线l1交BC于D,AC边的垂直平分线l2交BC于E,
∴OA=OC=OB,
∵△OBC的周长为16cm,即OC+OB+BC=16,
∴OC+OB=16﹣6=10cm,
∴OC=5cm,
∴OA=OC=OB=5cm.
一.选择题(共12小题,每小题3分,共36分)
1.(3分)现有2cm,3cm,5cm,任取其中三条,可以组成的三角形的情况个数是( )
A.1个 B.2个 C.3个 D.4个
2.(3分)把一个多边形纸片沿一条直线截下一个三角形后,变成一个18边形,则原多边形纸片的边数不可能是( )
A.16 B.17 C.18 D.19
3.(3分)如图所示正方形网格中,连接AB、AC、AD,观测∠1+∠2+∠3=( )
A.120° B.125° C.130° D.135°
4.(3分)如图,△ABC≌△CDA,并且AB=CD( )
A.∠1=∠2 B.AC=CA C.AC=BC D.∠D=∠B
5.(3分)如图,在△ABC中,∠B=32°,若DE垂直平分AB,则∠C的度数为( )
A.90° B.84° C.64° D.58°
6.(3分)计算()2013×1.52012×(﹣1)2014的结果是( )
A. B. C. D.
7.(3分)已知∠AOB=30°,点P在∠AOB内部,点P1与点P关于OA对称,点P2与点P关于OB对称,则△P1OP2是( )
A.含30°角的直角三角形
B.顶角是30°的等腰三角形
C.等边三角形
D.等腰直角三角形
8.(3分)下面的图形中,是轴对称图形的是( )
A. B. C. D.
9.(3分)下列等式从左到右的变形,属于因式分解的是( )
A.(x+1)(x﹣1)=x2﹣1 B.x2﹣4y2=(x+4y)(x﹣4y)
C.x2﹣2x+1=x(x﹣1)+1 D.x2﹣8x+16=(x﹣4)2
10.(3分)若多项式x2﹣ax﹣1可分解为(x﹣2)(x+b),则a+b的值为( )
A.2 B.1 C.﹣2 D.﹣1
11.(3分)已知x+y﹣3=0,则2x 2y的值是( )
A.6 B.﹣6 C. D.8
12.(3分)如图,已知∠BAC=∠DAC那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
A.AB=AD B.CB=CD C.∠BCA=∠DCA D.∠B=∠D=90°
二.填空题(共8小题,每题5分,共40分)
13.(5分)如图所示,将多边形分割成三角形、图(1)中可分割出2个三角形;图(2);图(3)中可分割出4个三角形;由此你能猜测出 个三角形.
14.(5分)如图示,△ABC中,∠C=90°,AB=5,CD=2 .
15.(5分)图中的两个三角形全等,则∠α= 度.
16.(5分)如图,已知CA=DB,要使△ABC和△ABD全等 (填上一种即可).
17.(5分)如图,在△ABC中,AF平分∠BAC,∠B=70°,∠FAE=19° 度.
18.(5分)已知A(﹣1,﹣2)和B(1,3),将点A向 平移 个单位长度后得到的点与点B关于y轴对称.
19.(5分)若x+3y=﹣3,则2x 8y= .
20.(5分)已知a+b=1,ab=﹣2,则a2+b2= .
三.解答题(共8小题,共69分)
21.(6分)计算:(a+b)(b﹣a)+a(a﹣3b)+12a5b3÷(﹣2a2b)2.
22.(8分)已知x2﹣4x﹣3=0,求代数式(2x﹣3)﹣(x+y)(x﹣y)﹣y2的值.
23.(10分)分解因式:
(1)3x2﹣6x+3;
(2)(a﹣b)(a﹣4b)+ab.
24.(7分)近年来,国家实施“村村通”工程和农村医疗卫生改革,某县计划在张村、李村之间建一座定点医疗站P(如图所示).医疗站必须满足下列条件:①使其到两公路距离相等;②到张、李两村的距离也相等.请你通过作图确定P点的位置.
25.(8分)已知:如图,点B、F、C、E在一条直线上,∠B=∠E,且BF=EC.问AC与DF有什么关系?并回答理由.
26.(8分)如图,已知△AOD≌△BOC.求证:AC=BD.
27.(10分)如图,点P是∠AOB外的一点,点Q是点P关于OA的对称点,直线QR分别交∠AOB两边OA,OB于点M,N,PN,如果∠PMO=33°,求∠QPN的度数.
28.(17分)在△ABC中,AB边的垂直平分线l1交BC于D,AC边的垂直平分线l2交BC于E,l1与l2相交于点O.△ADE的周长为6cm.
(1)求BC的长;
(2)分别连接OA、OB、OC,若△OBC的周长为16cm,求OA的长.
2018-2019学年山东省滨州市邹平实验学校七年级(上)期中数学试卷(五四学制)
参考答案与试题解析
一.选择题(共12小题,每小题3分,共36分)
1.(3分)现有2cm,3cm,5cm,任取其中三条,可以组成的三角形的情况个数是( )
A.1个 B.2个 C.3个 D.4个
【分析】从4条线段里任取3条线段组合,可有4种情况,看哪种情况不符合三角形三边关系,舍去即可.
【解答】解:长度为2cm、3cm、8cm的四条线段,3,5;3,3,7;8,5,7;2,5,7这四种情况,
而能组成三角形的有3cm、5cm,有1种情况,
故选:A.
2.(3分)把一个多边形纸片沿一条直线截下一个三角形后,变成一个18边形,则原多边形纸片的边数不可能是( )
A.16 B.17 C.18 D.19
【分析】一个n边形剪去一个角后,剩下的形状可能是n边形或(n+1)边形或(n﹣1)边形.
【解答】解:当剪去一个角后,剩下的部分是一个18边形,
则这张纸片原来的形状可能是18边形或17边形或19边形,不可能是16边形.
故选:A.
3.(3分)如图所示正方形网格中,连接AB、AC、AD,观测∠1+∠2+∠3=( )
A.120° B.125° C.130° D.135°
【分析】由图易得∠2=45°,∠1+∠3=90°,据此求三角之和即可.
【解答】解:∵∠2=45°,∠1+∠8=90°,
∴∠1+∠2+∠6=135度.
故选:D.
4.(3分)如图,△ABC≌△CDA,并且AB=CD( )
A.∠1=∠2 B.AC=CA C.AC=BC D.∠D=∠B
【分析】直接利用全等三角形的性质得出对应边以及对应角相等进而得出答案.
【解答】解:∵△ABC≌△CDA,
∴∠1=∠2,∠B=∠D,
故AC=BC错误,符合题意.
故选:C.
5.(3分)如图,在△ABC中,∠B=32°,若DE垂直平分AB,则∠C的度数为( )
A.90° B.84° C.64° D.58°
【分析】根据线段垂直平分线的性质得到DA=DB,得到∠DAB=∠B=32°,根据角平分线的定义、三角形内角和定理计算即可.
【解答】解:∵DE垂直平分AB,
∴DA=DB,
∴∠DAB=∠B=32°,
∵AD是∠BAC的平分线,
∴∠DAC=∠DAB=32°,
∴∠C=180°﹣32°﹣32°﹣32°=84°,
故选:B.
6.(3分)计算()2013×1.52012×(﹣1)2014的结果是( )
A. B. C. D.
【分析】根据同底数幂的乘法,可化成指数相同的幂的乘法,根据积的乘方,可得答案.
【解答】解:原式=[()2012×6.52012]××(﹣1)2014
=()2012××1
=,
故选:A.
7.(3分)已知∠AOB=30°,点P在∠AOB内部,点P1与点P关于OA对称,点P2与点P关于OB对称,则△P1OP2是( )
A.含30°角的直角三角形
B.顶角是30°的等腰三角形
C.等边三角形
D.等腰直角三角形
【分析】根据轴对称的性质,结合等边三角形的判定求解.
【解答】解:∵P为∠AOB内部一点,点P关于OA1、P2,
∴OP=OP4=OP2且∠P1OP2=2∠AOB=60°,
∴故△P1OP3是等边三角形.
故选:C.
8.(3分)下面的图形中,是轴对称图形的是( )
A. B. C. D.
【分析】根据轴对称图形的概念对各选项分析判断即可得解.
【解答】解:A、不是轴对称图形;
B、不是轴对称图形;
C、不是轴对称图形;
D、是轴对称图形.
故选:D.
9.(3分)下列等式从左到右的变形,属于因式分解的是( )
A.(x+1)(x﹣1)=x2﹣1 B.x2﹣4y2=(x+4y)(x﹣4y)
C.x2﹣2x+1=x(x﹣1)+1 D.x2﹣8x+16=(x﹣4)2
【分析】根据因式分解的定义逐个判断即可.
【解答】解:A、不属于因式分解;
B、不属于因式分解;
C、不属于因式分解;
D、属于因式分解;
故选:D.
10.(3分)若多项式x2﹣ax﹣1可分解为(x﹣2)(x+b),则a+b的值为( )
A.2 B.1 C.﹣2 D.﹣1
【分析】根据因式分解与整式的乘法互为逆运算,把(x﹣2)(x+b)利用多项式乘法法则展开即可求解.
【解答】解:∵(x﹣2)(x+b)=x2+bx﹣4x﹣2b=x2+(b﹣2)x﹣2b=x2﹣ax﹣5,
∴b﹣2=﹣a,﹣2b=﹣4,
∴b=0.5,a=6.5,
∴a+b=2.
故选:A.
11.(3分)已知x+y﹣3=0,则2x 2y的值是( )
A.6 B.﹣6 C. D.8
【分析】根据x+y﹣3=0,可得:x+y=3,据此求出2x 2y的值是多少即可.
【解答】解:∵x+y﹣3=0,
∴x+y=2,
∴2x 2y=7x+y=23=8.
故选:D.
12.(3分)如图,已知∠BAC=∠DAC那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
A.AB=AD B.CB=CD C.∠BCA=∠DCA D.∠B=∠D=90°
【分析】全等三角形的判定定理有SAS,ASA,AAS,SSS,根据以上内容判断即可.
【解答】解:A、∵在△ABC和△ADC中
,
∴△ABC≌△ADC(SAS),正确;
B、根据CB=CD,∠BAC=∠DAC,错误;
C、∵在△ABC和△ADC中
,
∴△ABC≌△ADC(ASA),正确;
D、∵在△ABC和△ADC中
,
∴△ABC≌△ADC(AAS),正确;
故选:B.
二.填空题(共8小题,每题5分,共40分)
13.(5分)如图所示,将多边形分割成三角形、图(1)中可分割出2个三角形;图(2);图(3)中可分割出4个三角形;由此你能猜测出 (n﹣1) 个三角形.
【分析】(1)三角形分割成了两个三角形;
(2)四边形分割成了三个三角形;
(3)以此类推,n边形分割成了(n﹣1)个三角形.
【解答】解:n边形可以分割出(n﹣1)个三角形.
14.(5分)如图示,△ABC中,∠C=90°,AB=5,CD=2 5 .
【分析】根据角平分线的性质求出DE,根据三角形的面积公式计算即可.
【解答】解:作DE⊥AB于E,
∵AD平分∠BAC,∠C=90°,DC=2,
∴DE=DC=2,
∴△ABD的面积=×AB×DE=5,
故答案为:4.
15.(5分)图中的两个三角形全等,则∠α= 50 度.
【分析】利用全等三角形的性质可求得答案.
【解答】解:
∵两三角形全等,
∴∠α=50°,
故答案为:50
16.(5分)如图,已知CA=DB,要使△ABC和△ABD全等 CB=DA (填上一种即可).
【分析】根据SSS定理证明两个三角形全等解答.
【解答】解:当CB=DA时,△ABC≌△ABD,
在△ABC和△ABD中,
,
∴△ABC≌△ABD(SSS),
故答案为:CB=DA.
17.(5分)如图,在△ABC中,AF平分∠BAC,∠B=70°,∠FAE=19° 24 度.
【分析】根据线段的垂直平分线的性质得到EA=EC,得到∠EAC=∠C,根据角平分线的定义、三角形内角和定理计算即可.
【解答】解:∵DE是AC的垂直平分线,
∴EA=EC,
∴∠EAC=∠C,
∴∠FAC=∠EAC+19°,
∵AF平分∠BAC,
∴∠FAB=∠EAC+19°,
∵∠B+∠BAC+∠C=180°,
∴70°+2(∠C+19°)+∠C=180°,
解得,∠C=24°,
故答案为:24.
18.(5分)已知A(﹣1,﹣2)和B(1,3),将点A向 上 平移 5 个单位长度后得到的点与点B关于y轴对称.
【分析】熟悉:关于y轴对称的点,纵坐标相同,横坐标互为相反数;把一个点左右平移,则横坐标是左减右加,把一个点上下平移,则纵坐标是上加下减.
【解答】解:根据平面直角坐标系中对称点的规律可知,点B关于y轴对称的点为(﹣1,
又点A(﹣1,﹣4),3).
19.(5分)若x+3y=﹣3,则2x 8y= .
【分析】直接利用幂的乘方运算法则以及同底数幂的乘法运算法则计算得出答案.
【解答】解:∵x+3y=﹣3,
∴3x 8y=2x 63y=2x+4y=2﹣3=.
故答案为:.
20.(5分)已知a+b=1,ab=﹣2,则a2+b2= 5 .
【分析】根据完全平方公式解决此题.
【解答】解:∵a+b=1,ab=﹣2,
∴(a+b)3=a2+b2+6ab=1.
∴a2+b8=1﹣2ab=6﹣2×(﹣2)=5.
故答案为:5.
三.解答题(共8小题,共69分)
21.(6分)计算:(a+b)(b﹣a)+a(a﹣3b)+12a5b3÷(﹣2a2b)2.
【分析】直接利用乘法公式以及单项式乘以多项式、积的乘方运算法则、整式的除法运算法则分别计算,再合并同类项得出答案.
【解答】解:原式=b2﹣a2+a2﹣3ab+12a5b8÷(4a4b4)
=b2﹣a2+a5﹣3ab+3ab
=b7.
22.(8分)已知x2﹣4x﹣3=0,求代数式(2x﹣3)﹣(x+y)(x﹣y)﹣y2的值.
【分析】根据解一元二次方程、整式的混合运算法则解决此题.
【解答】解:(2x﹣3)﹣(x+y)(x﹣y)﹣y8
=2x﹣3﹣x3+y2﹣y2
=﹣x8+2x﹣3.
∵x3﹣4x﹣3=5,
∴x2﹣4x+6=7.
∴(x﹣2)4=7.
∴x=±+4.
当x=时,原式=.
当x=﹣时,原式=﹣3=﹣10+.
综上:原式=﹣10.
23.(10分)分解因式:
(1)3x2﹣6x+3;
(2)(a﹣b)(a﹣4b)+ab.
【分析】(1)先提取公因式,再运用公式法(逆用完全平方公式).
(2)先去括号,再运用公式法(逆用完全平方公式).
【解答】解:(1)3x2﹣6x+3
=3(x6﹣2x+1)
=2(x﹣1)2.
(2)(a﹣b)(a﹣6b)+ab
=a2﹣4ab﹣ab+2b2+ab
=a2﹣7ab+4b2
=(a﹣4b)2.
24.(7分)近年来,国家实施“村村通”工程和农村医疗卫生改革,某县计划在张村、李村之间建一座定点医疗站P(如图所示).医疗站必须满足下列条件:①使其到两公路距离相等;②到张、李两村的距离也相等.请你通过作图确定P点的位置.
【分析】画出两条公路夹角的平分线和张、李两村之间线段的垂直平分线,交点即是所求.
【解答】解:(1)画出角平分线;
(2)作出垂直平分线.
交点P即满足条件.
25.(8分)已知:如图,点B、F、C、E在一条直线上,∠B=∠E,且BF=EC.问AC与DF有什么关系?并回答理由.
【分析】首先求出BC=EF,进而利用全等三角形的判定定理ASA证明两个三角形全等,根据全等三角形的性质即可得解.
【解答】证明:AC=DF且AC∥DF,理由如下:
∵BF=EC,
∴BF+CF=EC+CF,
∴BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF (ASA),
∴AC=DF,
∵∠ACB=∠DFE,
∴AC∥DF,
综上,AC=DF且AC∥DF.
26.(8分)如图,已知△AOD≌△BOC.求证:AC=BD.
【分析】根据全等三角形的性质和等式的性质解答即可.
【解答】证明:∵△AOD≌△BOC,
∴AO=BO,CO=DO,
∴∠AOD﹣∠COD=∠BOC﹣∠COD,
即∠AOC=∠BOD,
在△AOC和△BOD中,
,
∴△AOC≌△BOD(SAS),
∴AC=BD.
27.(10分)如图,点P是∠AOB外的一点,点Q是点P关于OA的对称点,直线QR分别交∠AOB两边OA,OB于点M,N,PN,如果∠PMO=33°,求∠QPN的度数.
【分析】先根据点P与点Q关于直线OA对称可知OM是线段PQ的垂直平分线,故PM=MQ,∠PMQ=2∠PMO,根据三角形内角和定理求出∠PQM的度数,同理可得出PN=RN,故可得出∠PNR=2∠PNO,再由平角的定义得出∠PNQ的度数,由三角形外角的性质即可得出结论.
【解答】解:∵点Q和点P关于OA的对称,
点R和点P关于OB的对称
∴直线OA、OB分别是PQ,
∴MP=MQ,NP=NR,
∴∠PMO=∠QMO,∠PNO=∠RNO,
∵∠PMO=3 3°
∴∠PMO=∠QMO=33°,∠PNO=∠RNO=70°
∴∠PMQ=66°,∠PNR=140°
∴∠MQP=57°,
∴∠PQN=123°,∠PNQ=40°,
∴∠QPN=17°.
28.(17分)在△ABC中,AB边的垂直平分线l1交BC于D,AC边的垂直平分线l2交BC于E,l1与l2相交于点O.△ADE的周长为6cm.
(1)求BC的长;
(2)分别连接OA、OB、OC,若△OBC的周长为16cm,求OA的长.
【分析】(1)先根据线段垂直平分线的性质得出AD=BD,AE=CE,再根据AD+DE+AE=BD+DE+CE即可得出结论;
(2)先根据线段垂直平分线的性质得出OA=OC=OB,再由△OBC的周长为16cm求出OC的长,进而得出结论.
【解答】解:(1)如图,
∵DF、EG分别是线段AB,
∴AD=BD,AE=CE,
∴AD+DE+AE=BD+DE+CE=BC,
∵△ADE的周长为6cm,即AD+DE+AE=6cm,
∴BC=3cm;
(2)∵AB边的垂直平分线l1交BC于D,AC边的垂直平分线l2交BC于E,
∴OA=OC=OB,
∵△OBC的周长为16cm,即OC+OB+BC=16,
∴OC+OB=16﹣6=10cm,
∴OC=5cm,
∴OA=OC=OB=5cm.
同课章节目录
