苏科版九年级数学上册 2.8 圆锥的侧面积(学案)(无答案)
文档属性
| 名称 | 苏科版九年级数学上册 2.8 圆锥的侧面积(学案)(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 70.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-01 09:53:37 | ||
图片预览

文档简介
2.8圆锥的侧面积(教案)
课 题 2.8圆锥的侧面积 主 备 主核
使用者 课 型 新 使用日期
【学习目标】 1.掌握圆锥的侧面积的计算公式,并会应用公式解决问题 2.经历探索圆锥侧面积计算公式的过程,发展学生的实践探索能力
第一次集体备课(通案) 第二次备课(个案)
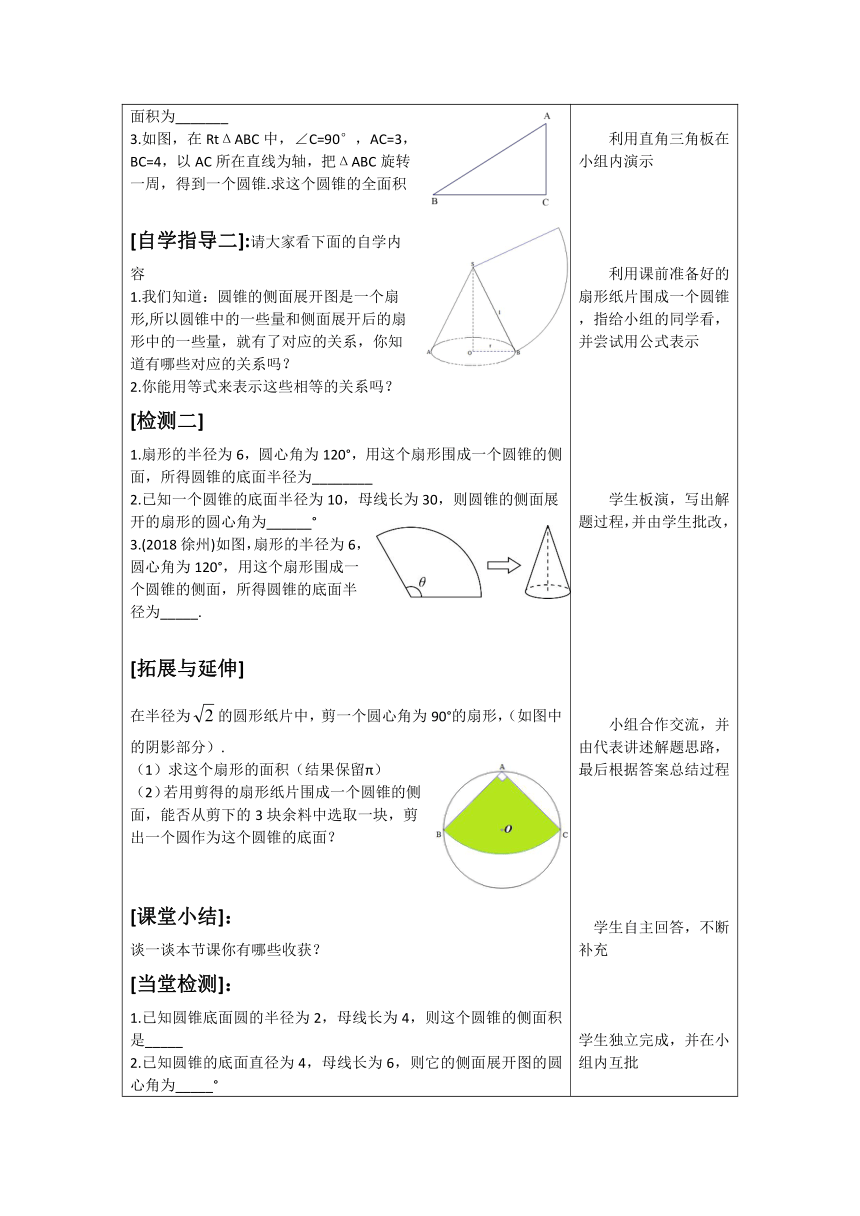
[复习引入] 1.扇形的面积公式是_________、_________ 2.圆锥是由一个_____和一个______围成的,它的_____是一个圆,______是一个曲面. 3.连接______与____________的线段叫做圆锥的高. 4.圆锥的轴截面是_________. [学习目标] 1.掌握圆锥的侧面积的计算公式,并会应用公式解决问题 2.经历探索圆锥侧面积计算公式的过程,发展学生的实践探索能力 [自学指导一]:请大家看书P86页的内容,看完例题 1.连接圆锥的_______和______________的线段叫做圆锥的母线,在右图中的母线是______________.这些母线在数量上______ 2.圆锥的高h,底面半径r和母线l之间的关系是__________________ 3.圆锥的侧面展开图是_____形 4.圆锥的侧面积公式是_______,你是怎样得到的这个公式? 5.你会求例题中容器盖铁皮的面积吗? 6分钟后比一比哪位同学掌握的最好! 例:用铁皮制作的圆锥形容器盖(如图),求这个容器盖铁皮的面积(精确到1 ) [检测一]: 1.已知圆锥的底面半径为3cm,母线长为5cm,则它的侧面积为_______ 2.已知圆锥的底面半径为6cm,高为8cm,则圆锥的侧面展开图的面积为_______ 3.如图,在RtΔABC中,∠C=90°,AC=3,BC=4,以AC所在直线为轴,把ΔABC旋转一周,得到一个圆锥.求这个圆锥的全面积 [自学指导二]:请大家看下面的自学内容 1.我们知道:圆锥的侧面展开图是一个扇形,所以圆锥中的一些量和侧面展开后的扇形中的一些量,就有了对应的关系,你知道有哪些对应的关系吗? 2.你能用等式来表示这些相等的关系吗? [检测二] 1.扇形的半径为6,圆心角为120°,用这个扇形围成一个圆锥的侧面,所得圆锥的底面半径为________ 2.已知一个圆锥的底面半径为10,母线长为30,则圆锥的侧面展开的扇形的圆心角为______° 3.(2018徐州)如图,扇形的半径为6,圆心角为120°,用这个扇形围成一个圆锥的侧面,所得圆锥的底面半径为_____. [拓展与延伸] 在半径为的圆形纸片中,剪一个圆心角为90°的扇形,(如图中的阴影部分). (1)求这个扇形的面积(结果保留π) (2)若用剪得的扇形纸片围成一个圆锥的侧面,能否从剪下的3块余料中选取一块,剪出一个圆作为这个圆锥的底面? [课堂小结]: 谈一谈本节课你有哪些收获? [当堂检测]: 1.已知圆锥底面圆的半径为2,母线长为4,则这个圆锥的侧面积是_____ 2.已知圆锥的底面直径为4,母线长为6,则它的侧面展开图的圆心角为_____° 3.用一张半径为20的扇形纸片制成一个圆锥,如果已知圆锥底面的半径为10,那么扇形的圆心角为______° [课堂作业]: (必做题):书P87页,习题2.8第2题 (选做题):《伴你学》 通过复习引入,让学生回忆旧知识,为下面新知识的学习作铺垫 让一个学生读学习目标 根据自学指导中的几个问题,学生在自学的基础上,结合小组交流来完成,然后在老师的带领下,由学生进行展示 学生小组交流,尝试用两种方法解决,由代表回答,同时,也为自学指导二作铺垫 学生独立完成,并在小组内互批 利用直角三角板在小组内演示 利用课前准备好的扇形纸片围成一个圆锥 ,指给小组的同学看,并尝试用公式表示 学生板演,写出解题过程,并由学生批改, 小组合作交流,并由代表讲述解题思路,最后根据答案总结过程 学生自主回答,不断补充 学生独立完成,并在小组内互批
第三次备课(反思)
本节课,学生对圆锥侧面积公式掌握的很好,但是,对与侧面展开的扇形有关的问题,一部分学生容易产生混淆,课后再让学生一帮一的教学,一定弄懂它们之间的对应关系;另外,课堂上小组活动充分,学生讨论问题的积极性非常高,并乐于动手操作,相互协作,圆满完成本节课的教学任务.
2.8圆锥的侧面积 (学案)
[复习引入]
1.扇形的面积公式是___________、___________
2.圆锥是由一个_____和一个______围成的,它的_____是一个圆,______是一个曲面.
3.连接______与____________的线段叫做圆锥的高.
4.圆锥的轴截面是_________.
[学习目标]
1.掌握圆锥的侧面积的计算公式,并会应用公式解决问题
2.经历探索圆锥侧面积计算公式的过程,发展学生的实践探索能力
[自学指导一]:请大家看书P86页的内容,看完例题
1.连接圆锥的_______和______________的线段叫做圆锥的母线,在右图中的母线是______________.这些母线在数量上________
2.圆锥的高h,底面半径r和母线l之间的关系是__________________
3.圆锥的侧面展开图是_____形
4.圆锥的侧面积公式是_______,你是怎样得到的这个公式?
5.你会求例题中容器盖铁皮的面积吗?
6分钟后比一比哪位同学掌握的最好!
例:用铁皮制作的圆锥形容器盖(如图),求这个容器盖铁皮的面积(精确到1 )
[检测一]:
1.已知圆锥的底面半径为3cm,母线长为5cm,则它的侧面积为_______
2.已知圆锥的底面半径为6cm,高为8cm,则圆锥的侧面展开图的面积为_______
3.如图,在RtΔABC中,∠C=90°,AC=3,BC=4,以AC所在直线为轴,把ΔABC旋转一周,得到一个圆锥.求这个圆锥的全面积
(
C
) (
n°
)[自学指导二]:请大家看下面的自学内容
我们知道:圆锥的侧面展开图是一个扇形,所以圆锥中的一些量和侧面展开后的扇形中的一些量,就有了对应的关系,你知道有哪些对应的关系吗?
①_______________________;②____________________
③_______________________
你能用等式来表示这些相等的关系吗?
①_______________________;②____________________
③_______________________
[检测二]
1.扇形的半径为6,圆心角为120°,用这个扇形围成一个圆锥的侧面,所得圆锥的底面半径为________
2.已知一个圆锥的底面半径为10,母线长为30,则圆锥的侧面展开的扇形的圆心角为______°
3.(2018徐州)如图,扇形的半径为6,圆心角为120°,用这个扇形围成一个圆锥的侧面,所得圆锥的底面半径为_____.
[拓展与延伸]
在半径为的圆形纸片中,剪一个圆心角为90°的扇形,(如图中的阴影部分).
(1)求这个扇形的面积(结果保留π)
(2)若用剪得的扇形纸片围成一个圆锥的侧面,能否从剪下的3块余料中选取一块,剪出一个圆作为这个圆锥的底面?
[课堂小结]:
谈一谈本节课你有哪些收获?
[当堂检测]:
1.已知圆锥底面圆的半径为2,母线长为4,则这个圆锥的侧面积是_____
2.已知圆锥的底面直径为4,母线长为6,则它的侧面展开图的圆心角为_____°
3.用一张半径为20的扇形纸片制成一个圆锥,如果已知圆锥底面的半径为10,那么扇形的圆心角为______°
[课堂作业]:(必做题):书P87页,习题2.8第2题; (选做题):《伴你学》
课 题 2.8圆锥的侧面积 主 备 主核
使用者 课 型 新 使用日期
【学习目标】 1.掌握圆锥的侧面积的计算公式,并会应用公式解决问题 2.经历探索圆锥侧面积计算公式的过程,发展学生的实践探索能力
第一次集体备课(通案) 第二次备课(个案)
[复习引入] 1.扇形的面积公式是_________、_________ 2.圆锥是由一个_____和一个______围成的,它的_____是一个圆,______是一个曲面. 3.连接______与____________的线段叫做圆锥的高. 4.圆锥的轴截面是_________. [学习目标] 1.掌握圆锥的侧面积的计算公式,并会应用公式解决问题 2.经历探索圆锥侧面积计算公式的过程,发展学生的实践探索能力 [自学指导一]:请大家看书P86页的内容,看完例题 1.连接圆锥的_______和______________的线段叫做圆锥的母线,在右图中的母线是______________.这些母线在数量上______ 2.圆锥的高h,底面半径r和母线l之间的关系是__________________ 3.圆锥的侧面展开图是_____形 4.圆锥的侧面积公式是_______,你是怎样得到的这个公式? 5.你会求例题中容器盖铁皮的面积吗? 6分钟后比一比哪位同学掌握的最好! 例:用铁皮制作的圆锥形容器盖(如图),求这个容器盖铁皮的面积(精确到1 ) [检测一]: 1.已知圆锥的底面半径为3cm,母线长为5cm,则它的侧面积为_______ 2.已知圆锥的底面半径为6cm,高为8cm,则圆锥的侧面展开图的面积为_______ 3.如图,在RtΔABC中,∠C=90°,AC=3,BC=4,以AC所在直线为轴,把ΔABC旋转一周,得到一个圆锥.求这个圆锥的全面积 [自学指导二]:请大家看下面的自学内容 1.我们知道:圆锥的侧面展开图是一个扇形,所以圆锥中的一些量和侧面展开后的扇形中的一些量,就有了对应的关系,你知道有哪些对应的关系吗? 2.你能用等式来表示这些相等的关系吗? [检测二] 1.扇形的半径为6,圆心角为120°,用这个扇形围成一个圆锥的侧面,所得圆锥的底面半径为________ 2.已知一个圆锥的底面半径为10,母线长为30,则圆锥的侧面展开的扇形的圆心角为______° 3.(2018徐州)如图,扇形的半径为6,圆心角为120°,用这个扇形围成一个圆锥的侧面,所得圆锥的底面半径为_____. [拓展与延伸] 在半径为的圆形纸片中,剪一个圆心角为90°的扇形,(如图中的阴影部分). (1)求这个扇形的面积(结果保留π) (2)若用剪得的扇形纸片围成一个圆锥的侧面,能否从剪下的3块余料中选取一块,剪出一个圆作为这个圆锥的底面? [课堂小结]: 谈一谈本节课你有哪些收获? [当堂检测]: 1.已知圆锥底面圆的半径为2,母线长为4,则这个圆锥的侧面积是_____ 2.已知圆锥的底面直径为4,母线长为6,则它的侧面展开图的圆心角为_____° 3.用一张半径为20的扇形纸片制成一个圆锥,如果已知圆锥底面的半径为10,那么扇形的圆心角为______° [课堂作业]: (必做题):书P87页,习题2.8第2题 (选做题):《伴你学》 通过复习引入,让学生回忆旧知识,为下面新知识的学习作铺垫 让一个学生读学习目标 根据自学指导中的几个问题,学生在自学的基础上,结合小组交流来完成,然后在老师的带领下,由学生进行展示 学生小组交流,尝试用两种方法解决,由代表回答,同时,也为自学指导二作铺垫 学生独立完成,并在小组内互批 利用直角三角板在小组内演示 利用课前准备好的扇形纸片围成一个圆锥 ,指给小组的同学看,并尝试用公式表示 学生板演,写出解题过程,并由学生批改, 小组合作交流,并由代表讲述解题思路,最后根据答案总结过程 学生自主回答,不断补充 学生独立完成,并在小组内互批
第三次备课(反思)
本节课,学生对圆锥侧面积公式掌握的很好,但是,对与侧面展开的扇形有关的问题,一部分学生容易产生混淆,课后再让学生一帮一的教学,一定弄懂它们之间的对应关系;另外,课堂上小组活动充分,学生讨论问题的积极性非常高,并乐于动手操作,相互协作,圆满完成本节课的教学任务.
2.8圆锥的侧面积 (学案)
[复习引入]
1.扇形的面积公式是___________、___________
2.圆锥是由一个_____和一个______围成的,它的_____是一个圆,______是一个曲面.
3.连接______与____________的线段叫做圆锥的高.
4.圆锥的轴截面是_________.
[学习目标]
1.掌握圆锥的侧面积的计算公式,并会应用公式解决问题
2.经历探索圆锥侧面积计算公式的过程,发展学生的实践探索能力
[自学指导一]:请大家看书P86页的内容,看完例题
1.连接圆锥的_______和______________的线段叫做圆锥的母线,在右图中的母线是______________.这些母线在数量上________
2.圆锥的高h,底面半径r和母线l之间的关系是__________________
3.圆锥的侧面展开图是_____形
4.圆锥的侧面积公式是_______,你是怎样得到的这个公式?
5.你会求例题中容器盖铁皮的面积吗?
6分钟后比一比哪位同学掌握的最好!
例:用铁皮制作的圆锥形容器盖(如图),求这个容器盖铁皮的面积(精确到1 )
[检测一]:
1.已知圆锥的底面半径为3cm,母线长为5cm,则它的侧面积为_______
2.已知圆锥的底面半径为6cm,高为8cm,则圆锥的侧面展开图的面积为_______
3.如图,在RtΔABC中,∠C=90°,AC=3,BC=4,以AC所在直线为轴,把ΔABC旋转一周,得到一个圆锥.求这个圆锥的全面积
(
C
) (
n°
)[自学指导二]:请大家看下面的自学内容
我们知道:圆锥的侧面展开图是一个扇形,所以圆锥中的一些量和侧面展开后的扇形中的一些量,就有了对应的关系,你知道有哪些对应的关系吗?
①_______________________;②____________________
③_______________________
你能用等式来表示这些相等的关系吗?
①_______________________;②____________________
③_______________________
[检测二]
1.扇形的半径为6,圆心角为120°,用这个扇形围成一个圆锥的侧面,所得圆锥的底面半径为________
2.已知一个圆锥的底面半径为10,母线长为30,则圆锥的侧面展开的扇形的圆心角为______°
3.(2018徐州)如图,扇形的半径为6,圆心角为120°,用这个扇形围成一个圆锥的侧面,所得圆锥的底面半径为_____.
[拓展与延伸]
在半径为的圆形纸片中,剪一个圆心角为90°的扇形,(如图中的阴影部分).
(1)求这个扇形的面积(结果保留π)
(2)若用剪得的扇形纸片围成一个圆锥的侧面,能否从剪下的3块余料中选取一块,剪出一个圆作为这个圆锥的底面?
[课堂小结]:
谈一谈本节课你有哪些收获?
[当堂检测]:
1.已知圆锥底面圆的半径为2,母线长为4,则这个圆锥的侧面积是_____
2.已知圆锥的底面直径为4,母线长为6,则它的侧面展开图的圆心角为_____°
3.用一张半径为20的扇形纸片制成一个圆锥,如果已知圆锥底面的半径为10,那么扇形的圆心角为______°
[课堂作业]:(必做题):书P87页,习题2.8第2题; (选做题):《伴你学》
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
