华师大版数学八上13.2.5全等三角形的判定(SSS)课件(15张PPT)
文档属性
| 名称 | 华师大版数学八上13.2.5全等三角形的判定(SSS)课件(15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-01 00:00:00 | ||
图片预览



文档简介
(共15张PPT)
13.2.5三角形全等的判定(SSS)
华东师大版·八年级上册
判断两个三角形全等的方法有几种
2.公理:SAS、ASA;
定理:AAS.
1.根据定义;
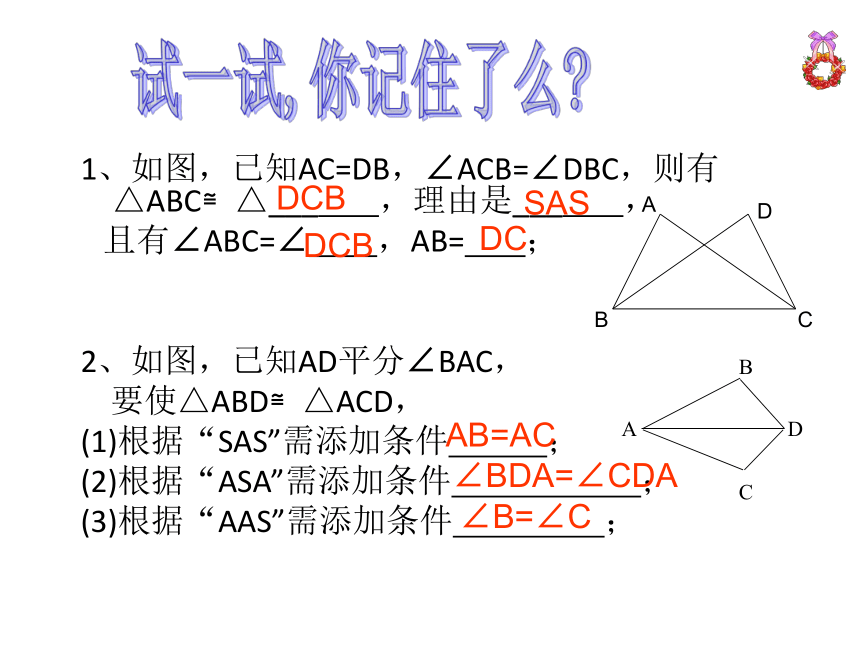
1、如图,已知AC=DB,∠ACB=∠DBC,则有△ABC≌△___ ,理由是___ ,
且有∠ABC=∠ ,AB= ;
2、如图,已知AD平分∠BAC,
要使△ABD≌△ACD,
(1)根据“SAS”需添加条件 ;
(2)根据“ASA”需添加条件 ;
(3)根据“AAS”需添加条件 ;
A
B
C
D
A
B
C
D
DCB
SAS
DCB
DC
AB=AC
∠BDA=∠CDA
∠B=∠C
若两个三角形有三个角对应相等,那么这两个三角形是否全等?
画△ABC,其中∠A=50°,∠B=60°, ∠C=70°.
50°
50°
60°
60°
A
B
C
A
B
C
A
B
C
70°
70°
三个角对应相等的两个三角形不一定全等
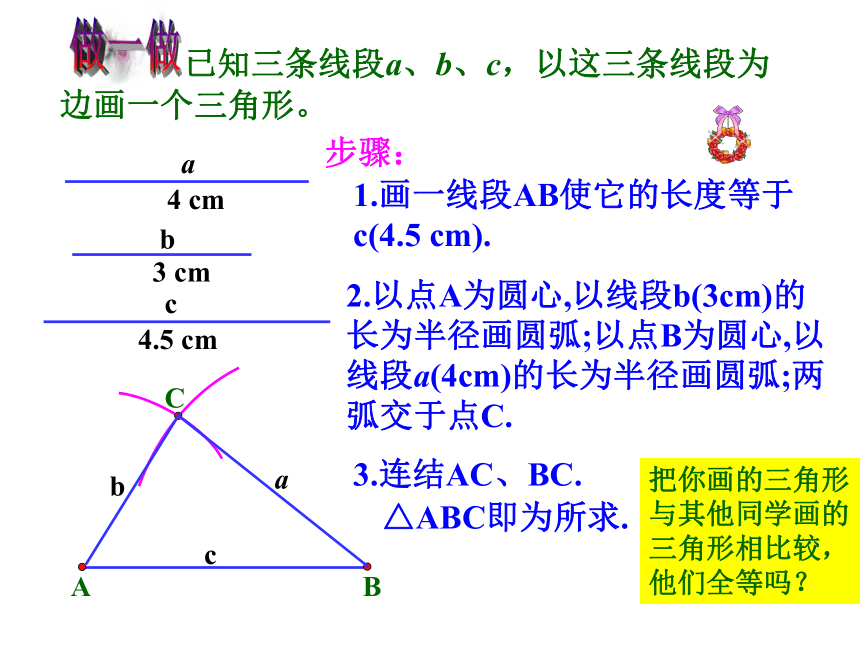
已知三条线段a、b、c,以这三条线段为边画一个三角形。
4 cm
a
3 cm
b
4.5 cm
c
步骤:
1.画一线段AB使它的长度等于 c(4.5 cm).
2.以点A为圆心,以线段b(3cm)的长为半径画圆弧;以点B为圆心,以线段a(4cm)的长为半径画圆弧;两弧交于点C.
3.连结AC、BC.
a
b
c
A
B
C
△ABC即为所求.
把你画的三角形与其他同学画的三角形相比较,他们全等吗?
A
B
C
D
E
F
〃
〃
\
\
≡
≡
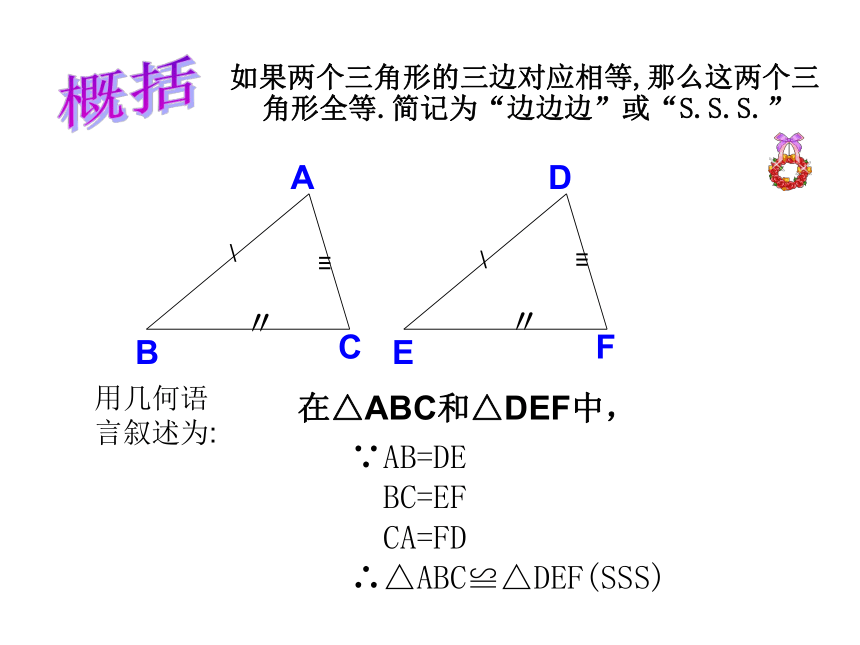
在△ABC和△DEF中,
用几何语言叙述为:
∵AB=DE
BC=EF
CA=FD
∴△ABC≌△DEF(SSS)
如果两个三角形的三边对应相等,那么这两个三角形全等.简记为“边边边”或“S.S.S.”
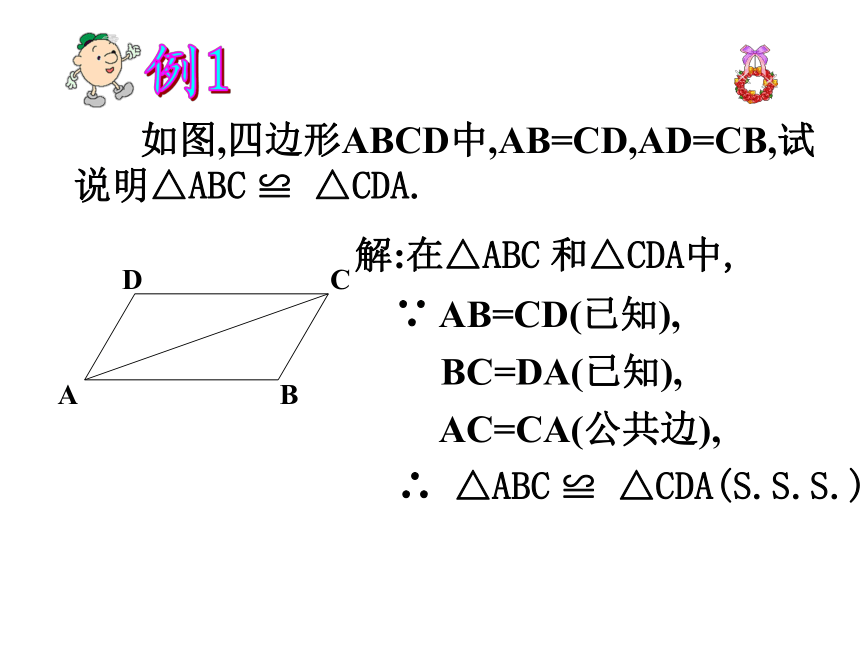
如图,四边形ABCD中,AB=CD,AD=CB,试说明△ABC ≌ △CDA.
解:在△ABC 和△CDA中,
∵ AB=CD(已知),
BC=DA(已知),
AC=CA(公共边),
∴ △ABC ≌ △CDA(S.S.S.)
A
B
C
D
D
A
B
C
(1) ∠B=∠D ;
(4)你还能得到什么结论?
(2) AB∥CD ;
(3) AD∥BC ;
如图,四边形ABCD中,AB=CD,AD=CB,试说明△ABC ≌ △CDA.
对应相等的元素 两边一角
两角一边
三角
三边
两边及其夹角 两边及其中一边的对角 两角及其夹边 两角及其中一角的对边
三角形是否全等
一定
(S.A.S.)
不一定
一定
(A.S.A.)
一定
(A.A.S.)
一定
(S.S.S.)
不一定
归纳
判定三角形全等时最少有几组边对应相等 最多有几组边
判定三角形全等时最少有几组角对应相等 最多有几组角
如图,AB=DC,AC=DB.
求证:△ABC≌△DCB.
A
B
C
D
O
思考:
(1)△ABO与△DCO全等吗?
(2)OB与OC相等吗
如图,AC、BD相交于点O,且AB=DC,AC=BD
求证: (1) ∠A=∠D
(2) OB=OC
A
B
C
D
O
如图,在△ABC中,AB=AC,E、F分别为AB、AC上的点,且AE=AF,BF与CE相交于点O。
A
O
F
E
B
C
图中有哪些全等的三角形?
△ABF≌△ACE(SAS)
△EBC≌△FCB(SSS)
△EBO≌△FCO(AAS)
如图, ∠ 1= ∠2,要使△ ABC ≌△ DCB,需增加的一个条件是_____________
A
B
C
D
O
1
2
①∠ABC=∠DCB(ASA)
②∠A=∠D(AAS)
③AC=DB(SAS)
小明家的衣橱上镶有两块全等的三角形玻璃装饰物,其中一块被打碎了,妈妈让小明到玻璃店配一块回来,请你说说小明该怎么办
链接生活
A
B
C
13.2.5三角形全等的判定(SSS)
华东师大版·八年级上册
判断两个三角形全等的方法有几种
2.公理:SAS、ASA;
定理:AAS.
1.根据定义;
1、如图,已知AC=DB,∠ACB=∠DBC,则有△ABC≌△___ ,理由是___ ,
且有∠ABC=∠ ,AB= ;
2、如图,已知AD平分∠BAC,
要使△ABD≌△ACD,
(1)根据“SAS”需添加条件 ;
(2)根据“ASA”需添加条件 ;
(3)根据“AAS”需添加条件 ;
A
B
C
D
A
B
C
D
DCB
SAS
DCB
DC
AB=AC
∠BDA=∠CDA
∠B=∠C
若两个三角形有三个角对应相等,那么这两个三角形是否全等?
画△ABC,其中∠A=50°,∠B=60°, ∠C=70°.
50°
50°
60°
60°
A
B
C
A
B
C
A
B
C
70°
70°
三个角对应相等的两个三角形不一定全等
已知三条线段a、b、c,以这三条线段为边画一个三角形。
4 cm
a
3 cm
b
4.5 cm
c
步骤:
1.画一线段AB使它的长度等于 c(4.5 cm).
2.以点A为圆心,以线段b(3cm)的长为半径画圆弧;以点B为圆心,以线段a(4cm)的长为半径画圆弧;两弧交于点C.
3.连结AC、BC.
a
b
c
A
B
C
△ABC即为所求.
把你画的三角形与其他同学画的三角形相比较,他们全等吗?
A
B
C
D
E
F
〃
〃
\
\
≡
≡
在△ABC和△DEF中,
用几何语言叙述为:
∵AB=DE
BC=EF
CA=FD
∴△ABC≌△DEF(SSS)
如果两个三角形的三边对应相等,那么这两个三角形全等.简记为“边边边”或“S.S.S.”
如图,四边形ABCD中,AB=CD,AD=CB,试说明△ABC ≌ △CDA.
解:在△ABC 和△CDA中,
∵ AB=CD(已知),
BC=DA(已知),
AC=CA(公共边),
∴ △ABC ≌ △CDA(S.S.S.)
A
B
C
D
D
A
B
C
(1) ∠B=∠D ;
(4)你还能得到什么结论?
(2) AB∥CD ;
(3) AD∥BC ;
如图,四边形ABCD中,AB=CD,AD=CB,试说明△ABC ≌ △CDA.
对应相等的元素 两边一角
两角一边
三角
三边
两边及其夹角 两边及其中一边的对角 两角及其夹边 两角及其中一角的对边
三角形是否全等
一定
(S.A.S.)
不一定
一定
(A.S.A.)
一定
(A.A.S.)
一定
(S.S.S.)
不一定
归纳
判定三角形全等时最少有几组边对应相等 最多有几组边
判定三角形全等时最少有几组角对应相等 最多有几组角
如图,AB=DC,AC=DB.
求证:△ABC≌△DCB.
A
B
C
D
O
思考:
(1)△ABO与△DCO全等吗?
(2)OB与OC相等吗
如图,AC、BD相交于点O,且AB=DC,AC=BD
求证: (1) ∠A=∠D
(2) OB=OC
A
B
C
D
O
如图,在△ABC中,AB=AC,E、F分别为AB、AC上的点,且AE=AF,BF与CE相交于点O。
A
O
F
E
B
C
图中有哪些全等的三角形?
△ABF≌△ACE(SAS)
△EBC≌△FCB(SSS)
△EBO≌△FCO(AAS)
如图, ∠ 1= ∠2,要使△ ABC ≌△ DCB,需增加的一个条件是_____________
A
B
C
D
O
1
2
①∠ABC=∠DCB(ASA)
②∠A=∠D(AAS)
③AC=DB(SAS)
小明家的衣橱上镶有两块全等的三角形玻璃装饰物,其中一块被打碎了,妈妈让小明到玻璃店配一块回来,请你说说小明该怎么办
链接生活
A
B
C
