新疆呼图壁县第一高级中学校2021-2022学年高一上学期期初模块测试数学试卷(Word版,含答案)
文档属性
| 名称 | 新疆呼图壁县第一高级中学校2021-2022学年高一上学期期初模块测试数学试卷(Word版,含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 512.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-31 00:00:00 | ||
图片预览



文档简介
呼图壁县第一中学2021-2022学年第一学期高一年级
期初 数学 模块测试卷
分 值: 100分 时 间:90分钟
一、单选题(共10小题,每题3分,共30分)
1.估计的值在下列哪两个整数之间( )
A.3和4之间 B.2和3之间 C.1和2之间 D.0和1之间
2.下列计算正确的是( )
A.a2 a3=a6 B.(a+b)(a﹣2b)=a2﹣2b2
C.(ab3)2=a2b6 D.5a﹣2a=3
3.在学校举行的“垃圾分类,人人有责”知识测试活动中,某小组的7名同学的测试成绩(单位:分)如下:90,80,90,85,85,90,95.则关于这组成绩数据,其众数和中位数分别是( )
A.85,90 B.90,85
C.90,90 D.85,85
4.如图,几何体由5个相同的小正方体构成,该几何体的主视图是( )
A. B. C. D.
5.如图,直线,则为( )
A.150° B.140°
C.130° D.120°
6.李明的身份证号码是,则李明的生日是( )
A.月日 B.月日 C.月日 D.月
7.2021年5月11日我国第七次人口普查数据出炉,与第五次、第六次人口普查数据相比较,我国人口总量持续增长.第五次人口普查全国总人口约12.95亿,第七次人口普查全国总人口约14.11亿,设从第五次到第七次人口普查总人口平均增长率为,则可列方程为( )
A. B.
C. D.
8.若关于x的方程ax2﹣x+2=0有两个不相等的实数根,则a的值可能是( )
A.﹣1 B.0 C.1 D.2
9.如图,一圆柱体的底面周长为3πcm,高AB为4cm,BC是上底面的直径.一只蚂蚁从点A出发,沿着圆柱的侧面爬行到点C,爬行的最短路程是( ).
A.3πcm B.5cm C.cm D.cm
10.四个相同的不透明的袋子都装有除颜色外无其它差别的小球.从这四个袋子中分别随机摸出一个球,摸到红球可能性最大的是( )
A.有1个红球和2个白球的袋子 B.有2个红球和3个白球的袋子
C.有3个红球和4个白球的袋子 D.有4个红球和5个白球的袋子
二、填空题(共6小题,每小题3分,共18分)
11.若式子在实数范围内有意义,则的取值范围是___________
12.分解因式:x2﹣1= .
13.若x:y=1:2,则=_____.
14.点A(m,n)到x轴的距离为3,到y轴的距离为2,则点A的坐标为______.
15.如图,已知等边三角形ABC的边长为4cm,分别以A、B、C为圆心,2cm为半径作三个扇形,则阴影部分的面积为___________.
16.用形状大小完全相同的等边三角形和正方形按如图所示的规律拼图案,即从第2个图案开始每个图案比前一个图案多4个等边三角形和1个正方形,则第2021个图案中等边三角形的个数为_______个.
三.解答题(共7小题,共52分)
17.(5分)计算:
(1)化简 (2)
18.(8分)如图,直线与双曲线交于,两点,与轴,轴分别交于,两点,且.
(1)求一次函数和反比例函数的解析式.
(2)将点沿轴平移得到点,若的面积为36,求点的坐标.
19.(6分)如图,已知.
(1)与全等吗?请说明理由;
(2)若,垂足为F,请说明线段;
20. (本题5分)解不等式组,并把解集表示在数轴上.
21.(本题6分))已知小光家住在楼高30米的楼上,他从楼顶测得旗杆顶端的俯角是60°,他又从离地面5米的窗口处测得旗杆顶端的仰角是45°,求旗杆的高度.
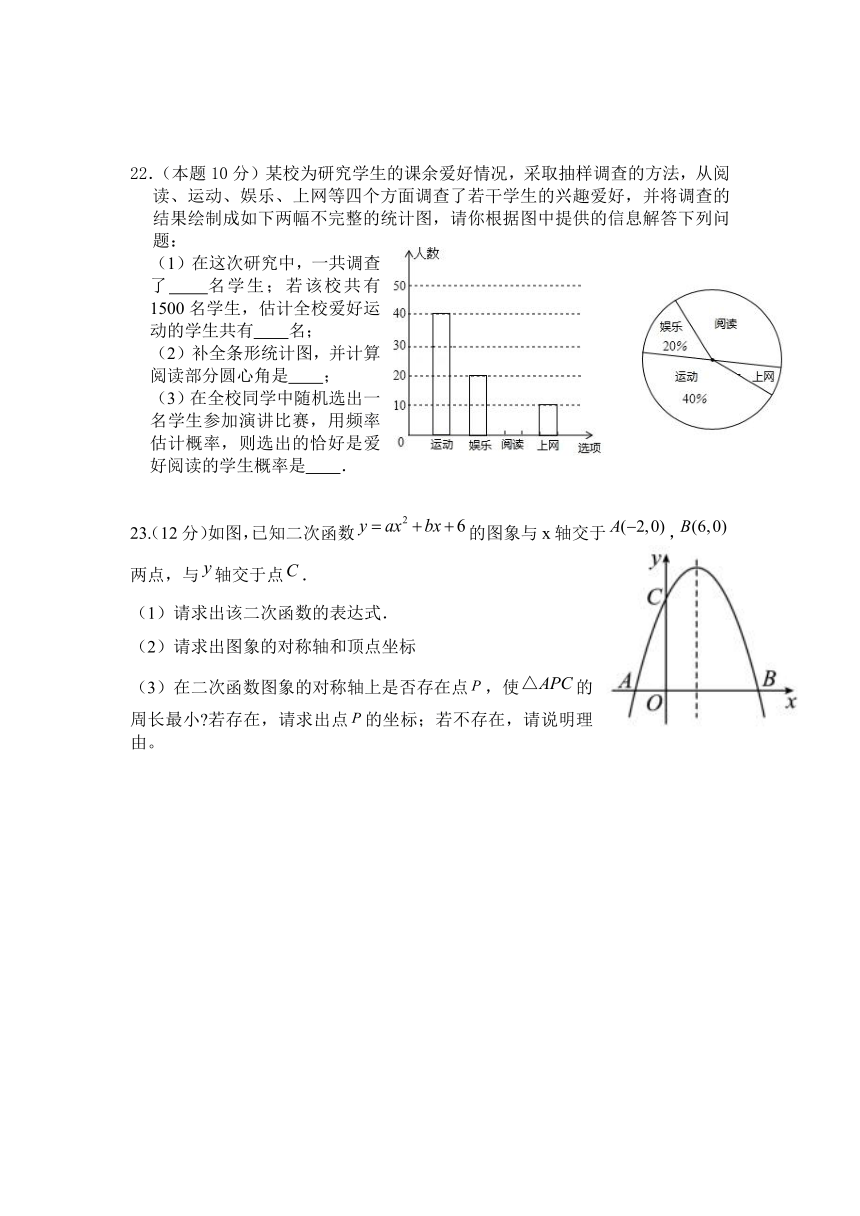
22.(本题10分)某校为研究学生的课余爱好情况,采取抽样调查的方法,从阅读、运动、娱乐、上网等四个方面调查了若干学生的兴趣爱好,并将调查的结果绘制成如下两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
(1)在这次研究中,一共调查了 名学生;若该校共有1500名学生,估计全校爱好运动的学生共有 名;
(2)补全条形统计图,并计算阅读部分圆心角是 ;
(3)在全校同学中随机选出一名学生参加演讲比赛,用频率估计概率,则选出的恰好是爱好阅读的学生概率是 .
23.(12分)如图,已知二次函数的图象与x轴交于,两点,与轴交于点.
(1)请求出该二次函数的表达式.
(2)请求出图象的对称轴和顶点坐标
(3)在二次函数图象的对称轴上是否存在点,使的周长最小 若存在,请求出点的坐标;若不存在,请说明理由。
数学答案
一、单选题
1.【答案】C
2.C
3.【答案】C
4.【答案】B
5.【答案】C
6.【答案】D
7.【答案】A
8.【答案】C
9.【答案】D
10.【答案】D
2、 填空题
11.【答案】x<2,
12.(x+1)(x﹣1)
13.【答案】
14.【答案】(2,3)或(-2,3)或(2,-3)或(2,-3).
15.【答案】
16、【答案】8082
三、解答题
17.
解:(1);
(2).
18、
(1)∵,
∴,
∵在中,
∴,
∴,
∴,
∴,
∴一次函数的解析式为:,
∴,
∴反比例函数的解析式为:;
(2)∵,解得或,
∴C(6,4),D(-3,-8),
∴,
∴,
∴点的坐标为或.
19.
解:(1)
证明:,
,
,
在和中,,
;
(2),理由如下;
延长到,使得,连接,如下图:
,
,
,
,
,
,
,
,
,
在和中,
,
,
,
,
,
.
20.(1)解不等式组,
解:由①得,x>﹣2,
由②得,x≤﹣1 故此不等式组的解集为:﹣2<x≤﹣1.
并把解集表示在数轴上
21.过作于,
∵,设
在中, (2分)
由题意得,
, (4分)
∴(米) (7分)
答:旗杆高为米. (8分)
22.(1)100;600;(2);(3)0.3
23. 解:(1)将,两点的坐标代入,得
解得
∴ 二次函数的表达式为.
(2)
,
∴ 二次函数图象的对称轴为直线,顶点坐标为.
(3)存在.如图,作点关于二次函数图象的对称轴的对称点,
连接A,交二次函数图象的对称轴于点,此时△的周长最小.
,∴ .
设直线A的表达式为,
则, 解得
∴直线A的表达式为.
当时,,即.
期初 数学 模块测试卷
分 值: 100分 时 间:90分钟
一、单选题(共10小题,每题3分,共30分)
1.估计的值在下列哪两个整数之间( )
A.3和4之间 B.2和3之间 C.1和2之间 D.0和1之间
2.下列计算正确的是( )
A.a2 a3=a6 B.(a+b)(a﹣2b)=a2﹣2b2
C.(ab3)2=a2b6 D.5a﹣2a=3
3.在学校举行的“垃圾分类,人人有责”知识测试活动中,某小组的7名同学的测试成绩(单位:分)如下:90,80,90,85,85,90,95.则关于这组成绩数据,其众数和中位数分别是( )
A.85,90 B.90,85
C.90,90 D.85,85
4.如图,几何体由5个相同的小正方体构成,该几何体的主视图是( )
A. B. C. D.
5.如图,直线,则为( )
A.150° B.140°
C.130° D.120°
6.李明的身份证号码是,则李明的生日是( )
A.月日 B.月日 C.月日 D.月
7.2021年5月11日我国第七次人口普查数据出炉,与第五次、第六次人口普查数据相比较,我国人口总量持续增长.第五次人口普查全国总人口约12.95亿,第七次人口普查全国总人口约14.11亿,设从第五次到第七次人口普查总人口平均增长率为,则可列方程为( )
A. B.
C. D.
8.若关于x的方程ax2﹣x+2=0有两个不相等的实数根,则a的值可能是( )
A.﹣1 B.0 C.1 D.2
9.如图,一圆柱体的底面周长为3πcm,高AB为4cm,BC是上底面的直径.一只蚂蚁从点A出发,沿着圆柱的侧面爬行到点C,爬行的最短路程是( ).
A.3πcm B.5cm C.cm D.cm
10.四个相同的不透明的袋子都装有除颜色外无其它差别的小球.从这四个袋子中分别随机摸出一个球,摸到红球可能性最大的是( )
A.有1个红球和2个白球的袋子 B.有2个红球和3个白球的袋子
C.有3个红球和4个白球的袋子 D.有4个红球和5个白球的袋子
二、填空题(共6小题,每小题3分,共18分)
11.若式子在实数范围内有意义,则的取值范围是___________
12.分解因式:x2﹣1= .
13.若x:y=1:2,则=_____.
14.点A(m,n)到x轴的距离为3,到y轴的距离为2,则点A的坐标为______.
15.如图,已知等边三角形ABC的边长为4cm,分别以A、B、C为圆心,2cm为半径作三个扇形,则阴影部分的面积为___________.
16.用形状大小完全相同的等边三角形和正方形按如图所示的规律拼图案,即从第2个图案开始每个图案比前一个图案多4个等边三角形和1个正方形,则第2021个图案中等边三角形的个数为_______个.
三.解答题(共7小题,共52分)
17.(5分)计算:
(1)化简 (2)
18.(8分)如图,直线与双曲线交于,两点,与轴,轴分别交于,两点,且.
(1)求一次函数和反比例函数的解析式.
(2)将点沿轴平移得到点,若的面积为36,求点的坐标.
19.(6分)如图,已知.
(1)与全等吗?请说明理由;
(2)若,垂足为F,请说明线段;
20. (本题5分)解不等式组,并把解集表示在数轴上.
21.(本题6分))已知小光家住在楼高30米的楼上,他从楼顶测得旗杆顶端的俯角是60°,他又从离地面5米的窗口处测得旗杆顶端的仰角是45°,求旗杆的高度.
22.(本题10分)某校为研究学生的课余爱好情况,采取抽样调查的方法,从阅读、运动、娱乐、上网等四个方面调查了若干学生的兴趣爱好,并将调查的结果绘制成如下两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
(1)在这次研究中,一共调查了 名学生;若该校共有1500名学生,估计全校爱好运动的学生共有 名;
(2)补全条形统计图,并计算阅读部分圆心角是 ;
(3)在全校同学中随机选出一名学生参加演讲比赛,用频率估计概率,则选出的恰好是爱好阅读的学生概率是 .
23.(12分)如图,已知二次函数的图象与x轴交于,两点,与轴交于点.
(1)请求出该二次函数的表达式.
(2)请求出图象的对称轴和顶点坐标
(3)在二次函数图象的对称轴上是否存在点,使的周长最小 若存在,请求出点的坐标;若不存在,请说明理由。
数学答案
一、单选题
1.【答案】C
2.C
3.【答案】C
4.【答案】B
5.【答案】C
6.【答案】D
7.【答案】A
8.【答案】C
9.【答案】D
10.【答案】D
2、 填空题
11.【答案】x<2,
12.(x+1)(x﹣1)
13.【答案】
14.【答案】(2,3)或(-2,3)或(2,-3)或(2,-3).
15.【答案】
16、【答案】8082
三、解答题
17.
解:(1);
(2).
18、
(1)∵,
∴,
∵在中,
∴,
∴,
∴,
∴,
∴一次函数的解析式为:,
∴,
∴反比例函数的解析式为:;
(2)∵,解得或,
∴C(6,4),D(-3,-8),
∴,
∴,
∴点的坐标为或.
19.
解:(1)
证明:,
,
,
在和中,,
;
(2),理由如下;
延长到,使得,连接,如下图:
,
,
,
,
,
,
,
,
,
在和中,
,
,
,
,
,
.
20.(1)解不等式组,
解:由①得,x>﹣2,
由②得,x≤﹣1 故此不等式组的解集为:﹣2<x≤﹣1.
并把解集表示在数轴上
21.过作于,
∵,设
在中, (2分)
由题意得,
, (4分)
∴(米) (7分)
答:旗杆高为米. (8分)
22.(1)100;600;(2);(3)0.3
23. 解:(1)将,两点的坐标代入,得
解得
∴ 二次函数的表达式为.
(2)
,
∴ 二次函数图象的对称轴为直线,顶点坐标为.
(3)存在.如图,作点关于二次函数图象的对称轴的对称点,
连接A,交二次函数图象的对称轴于点,此时△的周长最小.
,∴ .
设直线A的表达式为,
则, 解得
∴直线A的表达式为.
当时,,即.
同课章节目录
