人教版 六年级数学下册 3.1 第四课时 圆柱的体积 课件(共22张PPT)
文档属性
| 名称 | 人教版 六年级数学下册 3.1 第四课时 圆柱的体积 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-31 00:00:00 | ||
图片预览






文档简介
(共22张PPT)
人教版数学六年级(下)
第4课时 圆柱的体积(1)
圆柱与圆锥
3
1.圆柱
1.结合具体情境,探究并掌握圆柱体积的计算方法。
2. 经历观察、猜想、证明等数学活动过程,发展合情推理能力和初步的演绎推理能力,渗透数学思想,体验数学研究的方法。
3.通过对圆柱体积计算公式的推导、运用,体验数学问题的探究性和挑战性,感受数学思考过程的条理性和数学结论的确定性。
学习目标
【重点】
掌握圆柱体积的计算公式。
【难点】
圆柱体积计算公式的推导过程。
复习导入
什么是体积?
物体所占空间的大小是物体的体积。
怎样求长方体和正方体的体积?
正方体的体积=棱长×棱长×棱长
长方体的体积=长×宽×高
长
宽
高
棱长
V长方体=abh
V正方体=a3
我们会计算长方体和正方体的体积,圆柱的体积怎样计算呢?能不能将圆柱转化成我们学过的立体图形,计算出它的体积呢?
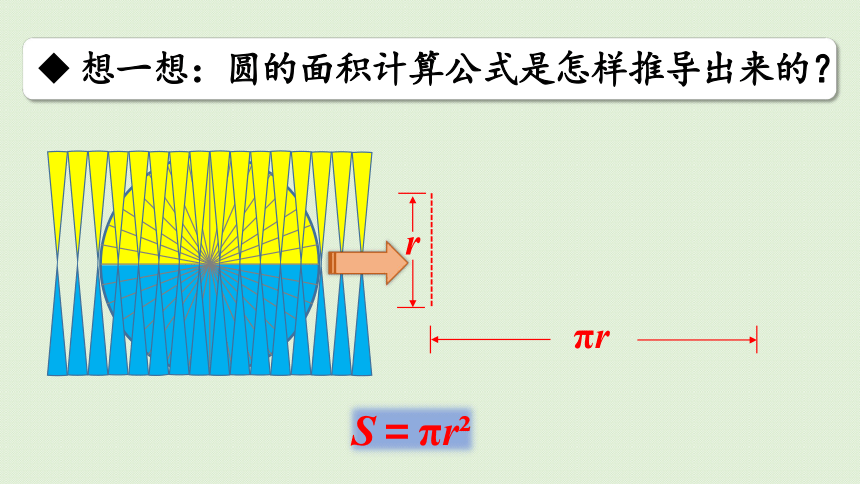
想一想:圆的面积计算公式是怎样推导出来的?
r
S=πr
πr
新知探究
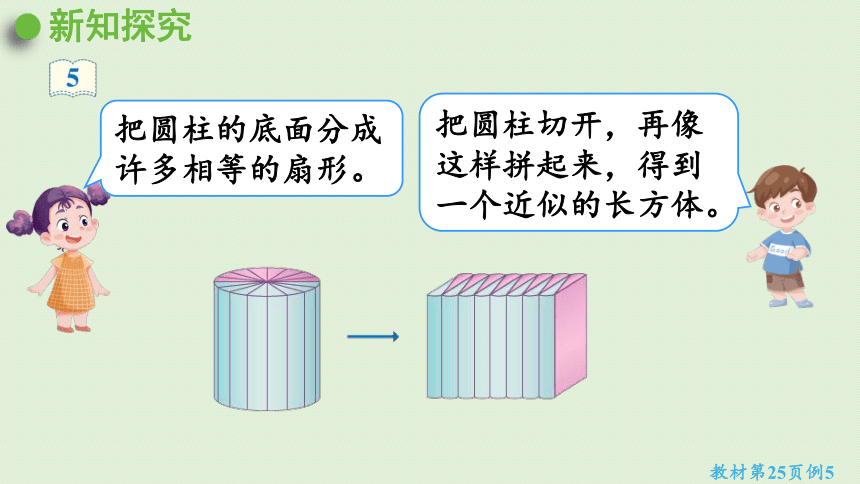
教材第25页例5
把圆柱的底面分成许多相等的扇形。
把圆柱切开,再像这样拼起来,得到一个近似的长方体。
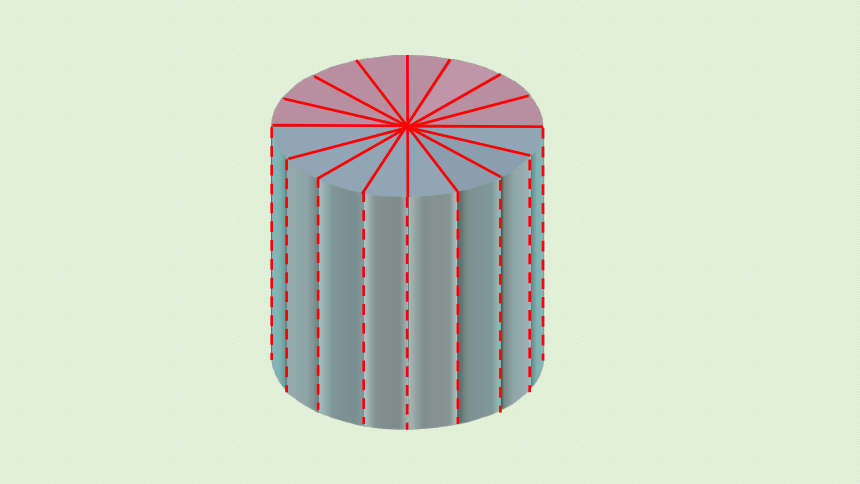
发现:分成的扇形越多,拼成的立体图形
就越接近于长方体。
把拼成的长方体与原来的圆柱比较,你能发现什么?
长方体的宽=圆柱的底面半径
底面半径
长方体的宽
长方体的长
圆柱底面周长的一半
长方体的长=圆柱底面周长的一半
长方体的底面积=圆柱的底面积
把拼成的长方体与原来的圆柱比较,你能发现什么?
底面半径
长方体的宽
长方体的长
圆柱底面周长的一半
长方体的底面积=圆柱的底面积
长方体的高
圆柱的高
长方体的高=圆柱的高
圆柱的体积=底面积 × 高
长方体的体积=底面积 × 高
V =
S
h
如果知道圆柱的底面半径r和高h,
V
圆柱体积计算公式是:
=
πr h
已知底面积和高:V = Sh
已知底面半径和高:V = πr2h
已知底面直径和高:V = π 2h
已知底面周长和高:V = π 2h
根据不同的条件可以推导出不同的公式。
课堂练习
1.求下面圆柱的体积。
(1)底面积是2 m ,高是0.7 m。
2×0.7=1.4( m )
答:圆柱的体积是1.4 m 。
(2)底面半径是3.2 dm,高是5 dm。
3.14×3.2 ×5=160.768(dm )
答:圆柱的体积是160.768 dm 。
V =Sh
V =πr2h
教材第22页“做一做”第1题
2.一根圆柱形木料,底面积为75 cm2 ,长 90 cm。
它的体积是多少?
75 ×90 =6750(cm3)
答:它的体积是6750cm3。
V =Sh
3.计算下面图形的体积。
C=31.4cm
h=8cm
高10dm
直径3dm
r =31.4÷3.14÷2
=5(cm)
S=3.14×5 ×8
=628(cm )
S=3.14×(3÷2) ×10
=3.14×2.25×10
=70.65(dm )
4.李家庄挖了一口圆柱形水井,地面以下的井
深10 m,井口直径为1 m。挖出的土有多少立
方米?
答:挖出的土有7.85立方米。
3.14 ×(1÷2) ×10=7.85(立方米)
已知底面直径和高:V = π ( ) 2h
教材第22页“做一做”第2题
同学们,这节课你有什么收获?
课堂小结
已知底面积和高:V = Sh
已知底面半径和高:V = πr2h
已知底面直径和高:V = π 2h
已知底面周长和高:V = π 2h
人教版数学六年级(下)
第4课时 圆柱的体积(1)
圆柱与圆锥
3
1.圆柱
1.结合具体情境,探究并掌握圆柱体积的计算方法。
2. 经历观察、猜想、证明等数学活动过程,发展合情推理能力和初步的演绎推理能力,渗透数学思想,体验数学研究的方法。
3.通过对圆柱体积计算公式的推导、运用,体验数学问题的探究性和挑战性,感受数学思考过程的条理性和数学结论的确定性。
学习目标
【重点】
掌握圆柱体积的计算公式。
【难点】
圆柱体积计算公式的推导过程。
复习导入
什么是体积?
物体所占空间的大小是物体的体积。
怎样求长方体和正方体的体积?
正方体的体积=棱长×棱长×棱长
长方体的体积=长×宽×高
长
宽
高
棱长
V长方体=abh
V正方体=a3
我们会计算长方体和正方体的体积,圆柱的体积怎样计算呢?能不能将圆柱转化成我们学过的立体图形,计算出它的体积呢?
想一想:圆的面积计算公式是怎样推导出来的?
r
S=πr
πr
新知探究
教材第25页例5
把圆柱的底面分成许多相等的扇形。
把圆柱切开,再像这样拼起来,得到一个近似的长方体。
发现:分成的扇形越多,拼成的立体图形
就越接近于长方体。
把拼成的长方体与原来的圆柱比较,你能发现什么?
长方体的宽=圆柱的底面半径
底面半径
长方体的宽
长方体的长
圆柱底面周长的一半
长方体的长=圆柱底面周长的一半
长方体的底面积=圆柱的底面积
把拼成的长方体与原来的圆柱比较,你能发现什么?
底面半径
长方体的宽
长方体的长
圆柱底面周长的一半
长方体的底面积=圆柱的底面积
长方体的高
圆柱的高
长方体的高=圆柱的高
圆柱的体积=底面积 × 高
长方体的体积=底面积 × 高
V =
S
h
如果知道圆柱的底面半径r和高h,
V
圆柱体积计算公式是:
=
πr h
已知底面积和高:V = Sh
已知底面半径和高:V = πr2h
已知底面直径和高:V = π 2h
已知底面周长和高:V = π 2h
根据不同的条件可以推导出不同的公式。
课堂练习
1.求下面圆柱的体积。
(1)底面积是2 m ,高是0.7 m。
2×0.7=1.4( m )
答:圆柱的体积是1.4 m 。
(2)底面半径是3.2 dm,高是5 dm。
3.14×3.2 ×5=160.768(dm )
答:圆柱的体积是160.768 dm 。
V =Sh
V =πr2h
教材第22页“做一做”第1题
2.一根圆柱形木料,底面积为75 cm2 ,长 90 cm。
它的体积是多少?
75 ×90 =6750(cm3)
答:它的体积是6750cm3。
V =Sh
3.计算下面图形的体积。
C=31.4cm
h=8cm
高10dm
直径3dm
r =31.4÷3.14÷2
=5(cm)
S=3.14×5 ×8
=628(cm )
S=3.14×(3÷2) ×10
=3.14×2.25×10
=70.65(dm )
4.李家庄挖了一口圆柱形水井,地面以下的井
深10 m,井口直径为1 m。挖出的土有多少立
方米?
答:挖出的土有7.85立方米。
3.14 ×(1÷2) ×10=7.85(立方米)
已知底面直径和高:V = π ( ) 2h
教材第22页“做一做”第2题
同学们,这节课你有什么收获?
课堂小结
已知底面积和高:V = Sh
已知底面半径和高:V = πr2h
已知底面直径和高:V = π 2h
已知底面周长和高:V = π 2h
