人教版六年级数学下册 3圆柱与圆锥 1圆柱 第6课时 求不规则物体的体积 课件(共16张PPT)
文档属性
| 名称 | 人教版六年级数学下册 3圆柱与圆锥 1圆柱 第6课时 求不规则物体的体积 课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-31 20:41:57 | ||
图片预览





文档简介
(共16张PPT)
人教版数学六年级(下)
第6课时 求不规则物体的体积
圆柱与圆锥
3
1.圆柱
1.能熟练运用圆柱的体积公式计算不规则物体的体积,体会转化思想。
2.感受数学与生活的联系,培养应用意识。
学习目标
【重点】熟练运用圆柱的体积公式计算不规则物体的体积。
【难点】将不规则物体转化为规则物体进行体积计算。
课堂导入
怎么计算不规则物体的容积呢?
可以转化为规则物体进行转化哦。
新知探究
新知探究
新知探究
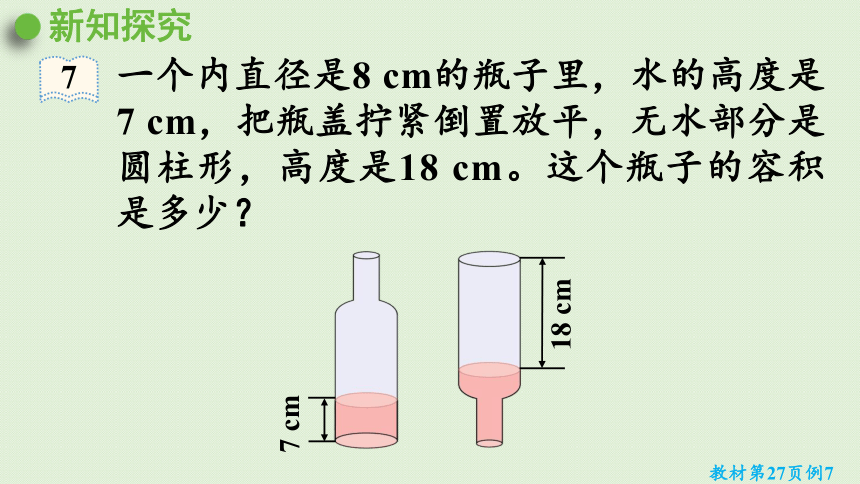
教材第27页例7
一个内直径是8 cm的瓶子里,水的高度是7 cm,把瓶盖拧紧倒置放平,无水部分是圆柱形,高度是18 cm。这个瓶子的容积是多少?
7
7 cm
18 cm
阅读与理解
这个瓶子不是一个完整的圆柱,无法直接计算容积。
能不能转化成圆柱呢?
分析与解答
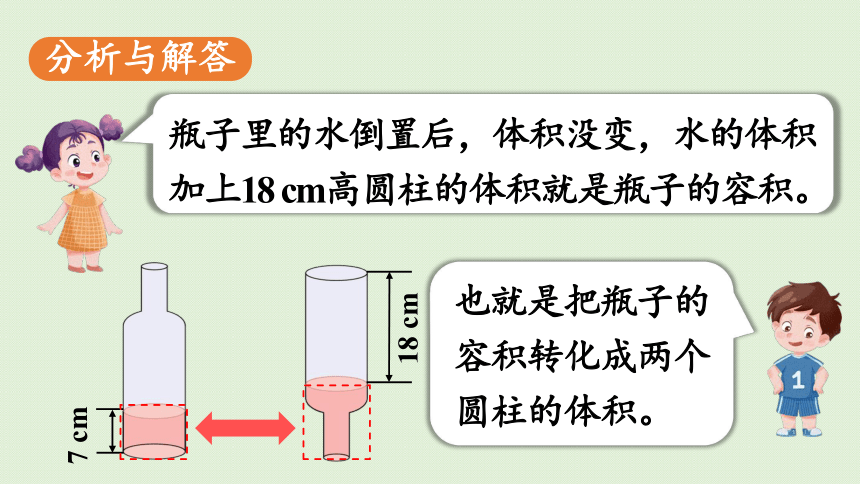
瓶子里的水倒置后,体积没变,水的体积加上18 cm高圆柱的体积就是瓶子的容积。
7 cm
18 cm
也就是把瓶子的容积转化成两个圆柱的体积。
答:瓶子的容积是1256 mL。
瓶子的容积:
3.14×(8÷2)2×7+3.14×(8÷2)2×18
=3.14×16×(7+18)
=3.14×16×25
=1256(cm3)
=1256(mL)
7 cm
18 cm
你还有别的解题思路吗?
求瓶子的容积转化为求一个高为7+18=25(cm)的圆柱的体积。
答:瓶子的容积是1256 mL。
瓶子的容积:
3.14×(8÷2)2×(7+18)
=3.14×16×25
=1256(cm3)
=1256(mL)
你还有别的解题思路吗?
回顾与反思
我们利用了体积不变的特性,把不规则图形转化成规则图形来计算。
在五年级计算梨的体积时也是用了转换的方法。
回顾与反思
课堂练习
1.一瓶装满的矿泉水,小明喝了一些,把瓶盖拧紧后倒置放平,无水部分高10 cm,内径是6 cm。小明喝了多少水?
10 cm
教材第27页“做一做”
喝水量=倒置后无水部分的体积,即高为10 cm、底面半径为6 cm的圆柱的体积。
答:瓶子的容积是1256 mL。
3.14×(6÷2)2×10
=3.14×9×10
=282.6(cm3)
=282.6(mL)
答:小明喝了282.6 mL水。
2.一个圆柱形玻璃容器的底面直径是10 cm,把一块完全浸在这个容器的水中的铁块取出后,水面下降2 cm。这块铁块的体积是多少?
铁块的体积=下降部分水的体积,即高为2 cm、底面半径为10 cm的圆柱的体积。
教材第29页第10题
3.14×(10÷2)2×2
=3.14×25×2
=157(cm3)
答:这块铁块的体积是157 cm3。
3.一个密封的瓶子里装着一些水(如图所示),已知瓶子的底面积为10 cm2,则瓶子的容积是多少?(忽略瓶壁的厚度)
瓶子的容积=圆柱①的体积+圆柱②的体积
①
②
10×[4+(7-5)]
=10×6
=60(cm3)
=60(mL)
答:瓶子的容积是60 mL。
拓展提升
如图所示,瓶子的高为25 cm,下面呈圆柱形。瓶子内装420克油,油面高14 cm;若将其倒立,则油面高18 cm。这个瓶子能装多少克油?
①
②
瓶子的容积=圆柱①②的体积和,即高为14+(25-18)=21(cm)的圆柱的体积。
420÷14×[14+(25-18)]
=30×21
=630(克)
答:这个瓶子能装630克油。
课堂小结
这节课你有什么收获?
求不规则物体的体积
利用体积不变的特性和转化法,将不规则物体转化为规则物体进行计算。
7 cm
18 cm
人教版数学六年级(下)
第6课时 求不规则物体的体积
圆柱与圆锥
3
1.圆柱
1.能熟练运用圆柱的体积公式计算不规则物体的体积,体会转化思想。
2.感受数学与生活的联系,培养应用意识。
学习目标
【重点】熟练运用圆柱的体积公式计算不规则物体的体积。
【难点】将不规则物体转化为规则物体进行体积计算。
课堂导入
怎么计算不规则物体的容积呢?
可以转化为规则物体进行转化哦。
新知探究
新知探究
新知探究
教材第27页例7
一个内直径是8 cm的瓶子里,水的高度是7 cm,把瓶盖拧紧倒置放平,无水部分是圆柱形,高度是18 cm。这个瓶子的容积是多少?
7
7 cm
18 cm
阅读与理解
这个瓶子不是一个完整的圆柱,无法直接计算容积。
能不能转化成圆柱呢?
分析与解答
瓶子里的水倒置后,体积没变,水的体积加上18 cm高圆柱的体积就是瓶子的容积。
7 cm
18 cm
也就是把瓶子的容积转化成两个圆柱的体积。
答:瓶子的容积是1256 mL。
瓶子的容积:
3.14×(8÷2)2×7+3.14×(8÷2)2×18
=3.14×16×(7+18)
=3.14×16×25
=1256(cm3)
=1256(mL)
7 cm
18 cm
你还有别的解题思路吗?
求瓶子的容积转化为求一个高为7+18=25(cm)的圆柱的体积。
答:瓶子的容积是1256 mL。
瓶子的容积:
3.14×(8÷2)2×(7+18)
=3.14×16×25
=1256(cm3)
=1256(mL)
你还有别的解题思路吗?
回顾与反思
我们利用了体积不变的特性,把不规则图形转化成规则图形来计算。
在五年级计算梨的体积时也是用了转换的方法。
回顾与反思
课堂练习
1.一瓶装满的矿泉水,小明喝了一些,把瓶盖拧紧后倒置放平,无水部分高10 cm,内径是6 cm。小明喝了多少水?
10 cm
教材第27页“做一做”
喝水量=倒置后无水部分的体积,即高为10 cm、底面半径为6 cm的圆柱的体积。
答:瓶子的容积是1256 mL。
3.14×(6÷2)2×10
=3.14×9×10
=282.6(cm3)
=282.6(mL)
答:小明喝了282.6 mL水。
2.一个圆柱形玻璃容器的底面直径是10 cm,把一块完全浸在这个容器的水中的铁块取出后,水面下降2 cm。这块铁块的体积是多少?
铁块的体积=下降部分水的体积,即高为2 cm、底面半径为10 cm的圆柱的体积。
教材第29页第10题
3.14×(10÷2)2×2
=3.14×25×2
=157(cm3)
答:这块铁块的体积是157 cm3。
3.一个密封的瓶子里装着一些水(如图所示),已知瓶子的底面积为10 cm2,则瓶子的容积是多少?(忽略瓶壁的厚度)
瓶子的容积=圆柱①的体积+圆柱②的体积
①
②
10×[4+(7-5)]
=10×6
=60(cm3)
=60(mL)
答:瓶子的容积是60 mL。
拓展提升
如图所示,瓶子的高为25 cm,下面呈圆柱形。瓶子内装420克油,油面高14 cm;若将其倒立,则油面高18 cm。这个瓶子能装多少克油?
①
②
瓶子的容积=圆柱①②的体积和,即高为14+(25-18)=21(cm)的圆柱的体积。
420÷14×[14+(25-18)]
=30×21
=630(克)
答:这个瓶子能装630克油。
课堂小结
这节课你有什么收获?
求不规则物体的体积
利用体积不变的特性和转化法,将不规则物体转化为规则物体进行计算。
7 cm
18 cm
