人教版六年级数学下册 4比例 整理和复习 课件(共17张PPT)
文档属性
| 名称 | 人教版六年级数学下册 4比例 整理和复习 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-31 20:45:33 | ||
图片预览




文档简介
(共17张PPT)
人教版数学六年级(下)
比例
4
整理和复习
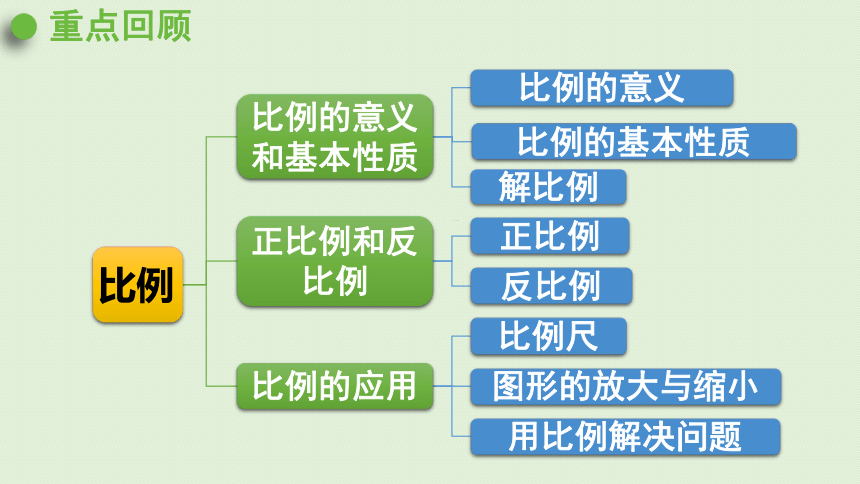
重点回顾
比例的意义和基本性质
比例的意义:表示两个比相等的式子叫做比例。
判断下面的比能否组成比例。
0.6∶0.2和
∶
3
4
1
4
∶ =
3
4
1
4
3
0.6∶0.2=3
能组成比例
比例的基本性质:在比例里,两个外项的积等于两个内项的积。
根据比例的基本性质,将算式改成比例。
比例的意义和基本性质
ad=bc。
如果 a∶b=c∶d或
a
b
c
d
=
(b、d≠0),
那么
× = ×
4
1
1
2
1
6
1
3
∶ = ∶
6
1
1
2
1
3
1
4
(答案不唯一)
解比例:根据比例的基本性质求出比例中的未知数。
小明与他在照片中的身高比是40∶1,他在照片中的身高是3 cm,他的实际身高是多少厘米?
解:设他的实际身高是x厘米。
答:他的实际身高是120厘米。
比例的意义和基本性质
x∶3=40∶1
x=40×3
x=120
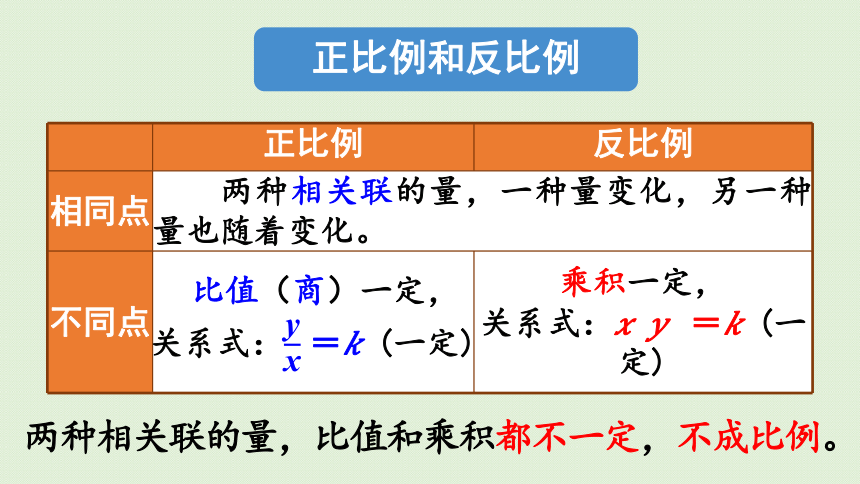
正比例和反比例
正比例 反比例
相同点 两种相关联的量,一种量变化,另一种量也随着变化。 不同点 比值(商)一定, 关系式: = (一定) 乘积一定,
关系式: = (一定)
两种相关联的量,比值和乘积都不一定,不成比例。
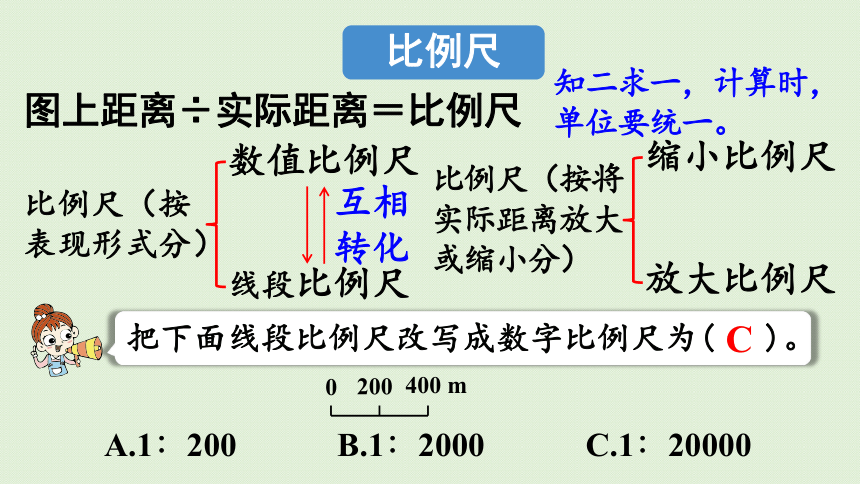
比例尺
图上距离÷实际距离=比例尺
知二求一,计算时,
单位要统一。
比例尺(按表现形式分)
数值比例尺
线段比例尺
互相
转化
把下面线段比例尺改写成数字比例尺为( )。
A.1∶200 B.1∶2000 C.1∶20000
0
200
400 m
C
比例尺(按将实际距离放大或缩小分)
缩小比例尺
放大比例尺
图形的放大与缩小
一数:数原图形各边各占几格。
二算:按给定的比算出图形各边放大或缩小后的长度。
三画:按算出的边长画出新图形。
把右面的长方形按3∶1放大,得到的图形的面积是( )cm2。
135
形状不变,大小变。
5 cm
3 cm
5×3=15(cm)
3×3=9(cm)
15×9=135(cm2)
用比例解决问题
用正比例、反比例解决问题有什么相同点和不同点?
都要找不变量
同
比值一定,用正比例解题
乘积一定,用反比例解题
异
练习巩固
比 比例
联系 比例是由两个比值相等的比组成的 区别 意义 表示两个数相除 表示两个比相等的式子
各部分 名称
基本性质 比的前项和后项同时乘或除以相同的数 (0除外),比值不变 在比例里,两个外项的积等于两个内项的积
2.4∶1.6=1.5
前项
比号
后项
比值
2.4∶1.6=60∶40
外项
内项
(教材第65页)
1.说一说:什么是比?什么是比例?比和比例有什么区别和联系?
2.解比例的依据是什么?解下面的比例。
解:5x4×6
∶∶4
解:4×
依据:比例的基本性质。
解:1.2x2.5×3
6.5∶x3.25∶4
解: 3.25x6.5×4
x8
2.解比例的依据是什么?解下面的比例。
依据:比例的基本性质。
3.下面每个表中的两个量,哪些成比例关系?成正比例关系还是反比例关系?哪些不成比例关系?
(1)从甲地到乙地的路程是240 km,汽车行驶的速度与时间如下表。
速度/(千米/时)
时间/时
40
6
50
4.8
60
4
80
3
100
2.4
因为行驶速度×行驶时间=路程(一定),所以行驶速度和行驶时间成反比例关系。
(2)圆锥的高是30 cm,它的体积与底面积如下表。
因为=×圆锥的高=10(一定),
底面积/cm2
体积/cm3
5
50
8
80
10
100
16
160
20
200
所以圆锥的体积与底面积成正比例关系。
3.下面每个表中的两个量,哪些成比例关系?成正比例关系还是反比例关系?哪些不成比例关系?
(3)圆的半径与圆的面积如下表。
因为=π×圆的半径(不一定),所以圆的面积与圆的半径不成比例关系。
半径/cm
面积/cm2
1
π
2
4π
3
9π
4
16π
5
25π
3.下面每个表中的两个量,哪些成比例关系?成正比例关系还是反比例关系?哪些不成比例关系?
4.(1)王叔叔开车从甲地到乙地,前2小时行了100 km。照这样的速度,从甲地到乙地一共要用3小时,甲乙两地相距多远?
速度一定,路程与时间成正比例关系。
=
x
3
100
2
2x=100×3
x=
100×3
2
x=150
解:设甲乙两地相距 x km。
答:甲乙两地相距 150 km。
4.(2)王叔叔开车从甲地到乙地一共用了3小时,每小时行 50 km。原路返回时每小时行 60 km,返回时用了多长时间?
路程一定,速度与时间成反比例关系。
60x=50×3
x=
50×3
60
x=2.5
解:设返回时用了x小时。
答:返回时用了2.5小时。
人教版数学六年级(下)
比例
4
整理和复习
重点回顾
比例的意义和基本性质
比例的意义:表示两个比相等的式子叫做比例。
判断下面的比能否组成比例。
0.6∶0.2和
∶
3
4
1
4
∶ =
3
4
1
4
3
0.6∶0.2=3
能组成比例
比例的基本性质:在比例里,两个外项的积等于两个内项的积。
根据比例的基本性质,将算式改成比例。
比例的意义和基本性质
ad=bc。
如果 a∶b=c∶d或
a
b
c
d
=
(b、d≠0),
那么
× = ×
4
1
1
2
1
6
1
3
∶ = ∶
6
1
1
2
1
3
1
4
(答案不唯一)
解比例:根据比例的基本性质求出比例中的未知数。
小明与他在照片中的身高比是40∶1,他在照片中的身高是3 cm,他的实际身高是多少厘米?
解:设他的实际身高是x厘米。
答:他的实际身高是120厘米。
比例的意义和基本性质
x∶3=40∶1
x=40×3
x=120
正比例和反比例
正比例 反比例
相同点 两种相关联的量,一种量变化,另一种量也随着变化。 不同点 比值(商)一定, 关系式: = (一定) 乘积一定,
关系式: = (一定)
两种相关联的量,比值和乘积都不一定,不成比例。
比例尺
图上距离÷实际距离=比例尺
知二求一,计算时,
单位要统一。
比例尺(按表现形式分)
数值比例尺
线段比例尺
互相
转化
把下面线段比例尺改写成数字比例尺为( )。
A.1∶200 B.1∶2000 C.1∶20000
0
200
400 m
C
比例尺(按将实际距离放大或缩小分)
缩小比例尺
放大比例尺
图形的放大与缩小
一数:数原图形各边各占几格。
二算:按给定的比算出图形各边放大或缩小后的长度。
三画:按算出的边长画出新图形。
把右面的长方形按3∶1放大,得到的图形的面积是( )cm2。
135
形状不变,大小变。
5 cm
3 cm
5×3=15(cm)
3×3=9(cm)
15×9=135(cm2)
用比例解决问题
用正比例、反比例解决问题有什么相同点和不同点?
都要找不变量
同
比值一定,用正比例解题
乘积一定,用反比例解题
异
练习巩固
比 比例
联系 比例是由两个比值相等的比组成的 区别 意义 表示两个数相除 表示两个比相等的式子
各部分 名称
基本性质 比的前项和后项同时乘或除以相同的数 (0除外),比值不变 在比例里,两个外项的积等于两个内项的积
2.4∶1.6=1.5
前项
比号
后项
比值
2.4∶1.6=60∶40
外项
内项
(教材第65页)
1.说一说:什么是比?什么是比例?比和比例有什么区别和联系?
2.解比例的依据是什么?解下面的比例。
解:5x4×6
∶∶4
解:4×
依据:比例的基本性质。
解:1.2x2.5×3
6.5∶x3.25∶4
解: 3.25x6.5×4
x8
2.解比例的依据是什么?解下面的比例。
依据:比例的基本性质。
3.下面每个表中的两个量,哪些成比例关系?成正比例关系还是反比例关系?哪些不成比例关系?
(1)从甲地到乙地的路程是240 km,汽车行驶的速度与时间如下表。
速度/(千米/时)
时间/时
40
6
50
4.8
60
4
80
3
100
2.4
因为行驶速度×行驶时间=路程(一定),所以行驶速度和行驶时间成反比例关系。
(2)圆锥的高是30 cm,它的体积与底面积如下表。
因为=×圆锥的高=10(一定),
底面积/cm2
体积/cm3
5
50
8
80
10
100
16
160
20
200
所以圆锥的体积与底面积成正比例关系。
3.下面每个表中的两个量,哪些成比例关系?成正比例关系还是反比例关系?哪些不成比例关系?
(3)圆的半径与圆的面积如下表。
因为=π×圆的半径(不一定),所以圆的面积与圆的半径不成比例关系。
半径/cm
面积/cm2
1
π
2
4π
3
9π
4
16π
5
25π
3.下面每个表中的两个量,哪些成比例关系?成正比例关系还是反比例关系?哪些不成比例关系?
4.(1)王叔叔开车从甲地到乙地,前2小时行了100 km。照这样的速度,从甲地到乙地一共要用3小时,甲乙两地相距多远?
速度一定,路程与时间成正比例关系。
=
x
3
100
2
2x=100×3
x=
100×3
2
x=150
解:设甲乙两地相距 x km。
答:甲乙两地相距 150 km。
4.(2)王叔叔开车从甲地到乙地一共用了3小时,每小时行 50 km。原路返回时每小时行 60 km,返回时用了多长时间?
路程一定,速度与时间成反比例关系。
60x=50×3
x=
50×3
60
x=2.5
解:设返回时用了x小时。
答:返回时用了2.5小时。
