人教版六年级数学下册 4比例 1比例的意义和基本性质 第2课时 比例的基本性质 课件(共18张PPT)
文档属性
| 名称 | 人教版六年级数学下册 4比例 1比例的意义和基本性质 第2课时 比例的基本性质 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 663.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-31 20:46:30 | ||
图片预览




文档简介
(共18张PPT)
人教版数学六年级(下)
比例
第2课时 比例的基本性质
4
1.比例的意义和基本性质
1.知道比例的各部分名称,掌握比例的基本性质,能运用比例的基本性质判断两个比能否组成比例。
2.通过观察思考、计算验证、交流讨论等学习方式,在数学活动中自主获取知识,培养数学思维。
3.感悟数学知识的内在联系,培养初步的数学辩证思想。
学习目标
【重点】
理解比例的基本性质。
【难点】
应用比例的基本性质判断两个比能否
组成比例。
试着写出2个比值是1.5的比。
2.4∶1.6=1.5
60∶40=1.5
课堂导入
你能把它们组成比例吗?
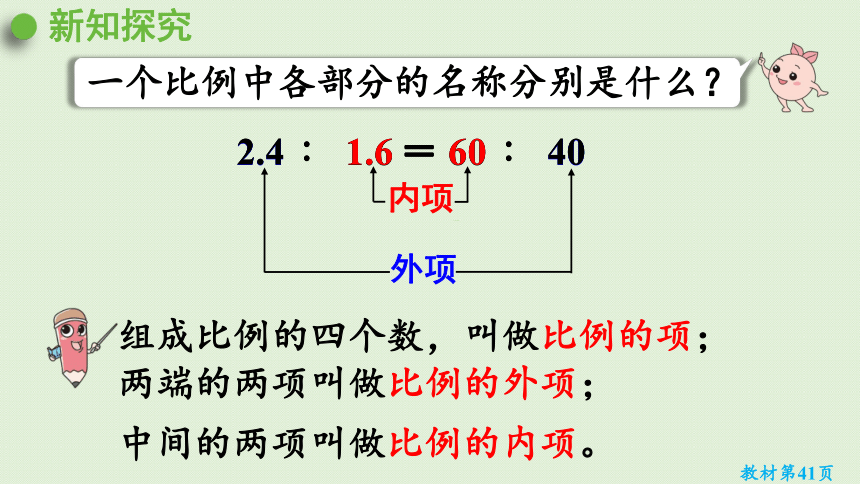
组成比例的四个数,叫做比例的项;
内项
外项
两端的两项叫做比例的外项;
中间的两项叫做比例的内项。
新知探究
2.4 ∶ 1.6= 60 ∶ 40
一个比例中各部分的名称分别是什么?
教材第41页
2.4 ∶ 1.6= 60 ∶ 40
2.4 ∶ 1.6= 60 ∶ 40
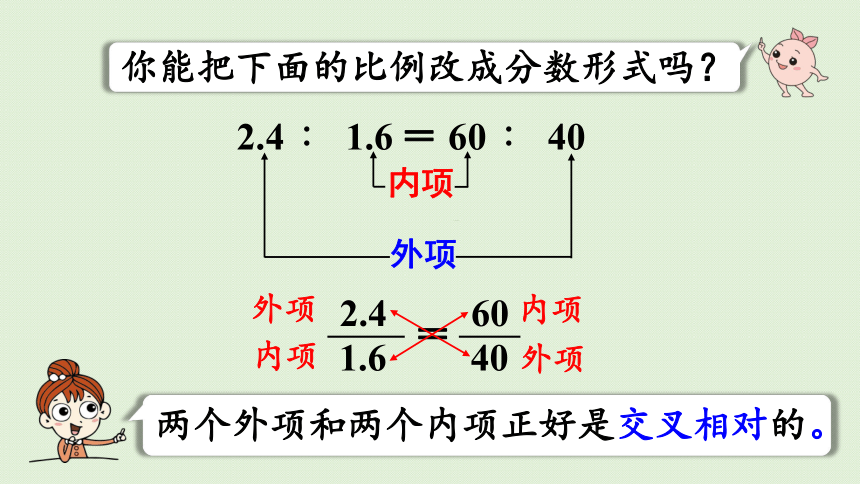
你能把下面的比例改成分数形式吗?
2.4 ∶ 1.6= 60 ∶ 40
内项
外项
2.4
1.6
60
40
=
内项
内项
外项
外项
两个外项和两个内项正好是交叉相对的。
3
5
9
15
=
(2)
(1)2.4∶1.6=60∶40
外项积:
内项积:
3×15=45
5×9=45
2.4×40=96
1.6×60=96
3
15
5
9
内项
外项
教材第41页例1
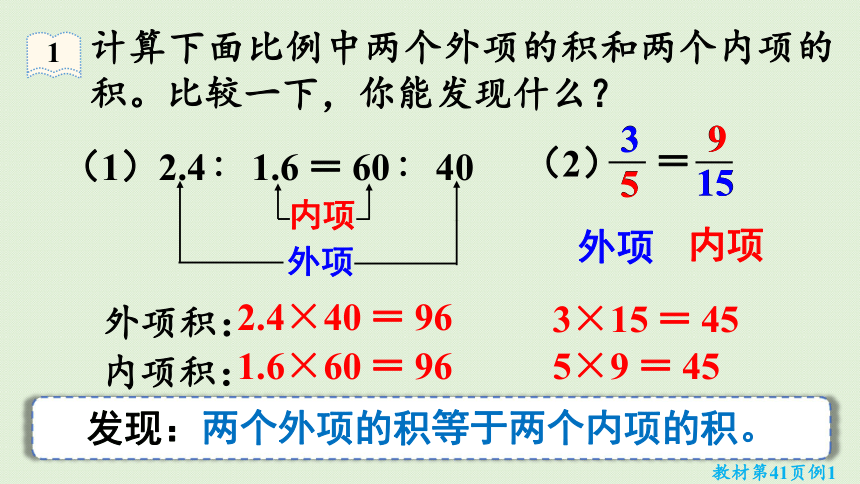
计算下面比例中两个外项的积和两个内项的积。比较一下,你能发现什么?
1
内项
外项
发现:两个外项的积等于两个内项的积。
你能举一个例子,验证你的发现吗?
∶ ∶
1
5
4
1
1
2
5
8
=
外项积:
内项积:
× =
1
4
1
2
1
8
× =
1
5
5
8
1
8
在比例里,两个外项的积等于两个内项的积。
这叫做比例的基本性质。
在比例里,两个外项的积等于两个内项的积。
这叫做比例的基本性质。
你能用字母表示这个性质吗?
ad=bc。
如果 a∶b=c∶d或
a
b
c
d
=
(b、d≠0),
那么
比和比例有什么区别和联系?
比 比例
意义
各部分名称
基本性质
表示两个数相除。
表示两个比相等的式子。
a : b=-(b≠0)
ab
…前项
…比号
…后项
…比值
比的前项和后项同时乘或除以一个相同的数(0除外),比值不变。
在比例里,两个外项的积等于两个内项的积。
内项
外项
a :b = c :d或-=-
ab
cd
(b、d≠0)
课堂练习
1.应用比例的基本性质,判断下面哪组中的两个比可以组成比例。
(1)6∶3和8∶5
(2)0.2∶2.5和4∶50
6×5=30
3×8=24
6×5≠3×8
不能组成比例
0.2×50=10
2.5×4=10
0.2×50=2.5×4
能组成比例
教材第41页“做一做”
1.应用比例的基本性质,判断下面哪组中的两个比可以组成比例。
(3)
∶ 和 ∶
4
1
1
3
1
6
1
2
(4)
∶ 和 ∶
5
1.2
3
4
4
5
能组成比例
× =
1
4
1
3
1
12
× = ×
1
4
1
3
1
6
1
2
× =
1
2
1
6
1
12
1.2×5=6
× =
4
5
3
4
0.6
× ≠ ×
5
1.2
3
4
4
5
不能组成比例
2.填空。
(3)如果A×5=B×8(A、B均不为0),那么A∶B=( )∶( )。
8
5
(1)在一个比例中,两个外项的积是10,一个内项是8,另一个内项是( )。
5
4
(2)在一个比例里,两个外项互为倒数,其中一个内项是 ,另一个内项是( )。
4
9
10÷8=
5
4
9
4
3. 4∶5=12∶15,如果内项5增加5,那么外项4应该增加多少才能使比例成立?
(4+x)∶(5+5)=12∶15
(4+x)∶10=12∶15
15(4+x)=12×10
解:设外项4应该增加x才能使比例成立。
15x=60
x=4
答:外项4应该增加4才能使比例成立。
拓展提升
一个比例的两个内项分别是0.6和1.5,两个比的比值都是 ,你能写出这个比例吗?
9
4
先写出比例结构,再根据比值把比例分成两个单独的比,把求比例的外项转化为求比的前项或后项。
解:设比例的两个外项分别是a和b。可以得到比例
a∶0.6=1.5∶b或a∶1.5=0.6∶b。
a∶0.6=
9
4
1.5∶b=
9
4
a=0.6×
9
4
a=
4
15
b=1.5÷
9
4
b=
27
8
解:设比例的两个外项分别是a和b。可以得到比例
a∶0.6=1.5∶b或a∶1.5=0.6∶b。
a∶1.5=
9
4
0.6∶b=
9
4
a=1.5×
9
4
a=
2
3
b=0.6÷
9
4
b=
27
20
∶ = ∶
20
27
2
3
1.5
0.6
答:这个比例是 或
∶ = ∶
8
27
4
15
0.6
1.5
。
课堂小结
1. 比例各部分的名称: 组成比例的四个数,叫做比例的项。两端的两项叫做比例的外项,中间的两项叫做比例的内项。
2. 比例的基本性质:在比例里,两个外项的积等于两个内项的积。这叫做比例的基本性质。
(判断两个比能否成比例的依据)
这节课你有什么收获?
人教版数学六年级(下)
比例
第2课时 比例的基本性质
4
1.比例的意义和基本性质
1.知道比例的各部分名称,掌握比例的基本性质,能运用比例的基本性质判断两个比能否组成比例。
2.通过观察思考、计算验证、交流讨论等学习方式,在数学活动中自主获取知识,培养数学思维。
3.感悟数学知识的内在联系,培养初步的数学辩证思想。
学习目标
【重点】
理解比例的基本性质。
【难点】
应用比例的基本性质判断两个比能否
组成比例。
试着写出2个比值是1.5的比。
2.4∶1.6=1.5
60∶40=1.5
课堂导入
你能把它们组成比例吗?
组成比例的四个数,叫做比例的项;
内项
外项
两端的两项叫做比例的外项;
中间的两项叫做比例的内项。
新知探究
2.4 ∶ 1.6= 60 ∶ 40
一个比例中各部分的名称分别是什么?
教材第41页
2.4 ∶ 1.6= 60 ∶ 40
2.4 ∶ 1.6= 60 ∶ 40
你能把下面的比例改成分数形式吗?
2.4 ∶ 1.6= 60 ∶ 40
内项
外项
2.4
1.6
60
40
=
内项
内项
外项
外项
两个外项和两个内项正好是交叉相对的。
3
5
9
15
=
(2)
(1)2.4∶1.6=60∶40
外项积:
内项积:
3×15=45
5×9=45
2.4×40=96
1.6×60=96
3
15
5
9
内项
外项
教材第41页例1
计算下面比例中两个外项的积和两个内项的积。比较一下,你能发现什么?
1
内项
外项
发现:两个外项的积等于两个内项的积。
你能举一个例子,验证你的发现吗?
∶ ∶
1
5
4
1
1
2
5
8
=
外项积:
内项积:
× =
1
4
1
2
1
8
× =
1
5
5
8
1
8
在比例里,两个外项的积等于两个内项的积。
这叫做比例的基本性质。
在比例里,两个外项的积等于两个内项的积。
这叫做比例的基本性质。
你能用字母表示这个性质吗?
ad=bc。
如果 a∶b=c∶d或
a
b
c
d
=
(b、d≠0),
那么
比和比例有什么区别和联系?
比 比例
意义
各部分名称
基本性质
表示两个数相除。
表示两个比相等的式子。
a : b=-(b≠0)
ab
…前项
…比号
…后项
…比值
比的前项和后项同时乘或除以一个相同的数(0除外),比值不变。
在比例里,两个外项的积等于两个内项的积。
内项
外项
a :b = c :d或-=-
ab
cd
(b、d≠0)
课堂练习
1.应用比例的基本性质,判断下面哪组中的两个比可以组成比例。
(1)6∶3和8∶5
(2)0.2∶2.5和4∶50
6×5=30
3×8=24
6×5≠3×8
不能组成比例
0.2×50=10
2.5×4=10
0.2×50=2.5×4
能组成比例
教材第41页“做一做”
1.应用比例的基本性质,判断下面哪组中的两个比可以组成比例。
(3)
∶ 和 ∶
4
1
1
3
1
6
1
2
(4)
∶ 和 ∶
5
1.2
3
4
4
5
能组成比例
× =
1
4
1
3
1
12
× = ×
1
4
1
3
1
6
1
2
× =
1
2
1
6
1
12
1.2×5=6
× =
4
5
3
4
0.6
× ≠ ×
5
1.2
3
4
4
5
不能组成比例
2.填空。
(3)如果A×5=B×8(A、B均不为0),那么A∶B=( )∶( )。
8
5
(1)在一个比例中,两个外项的积是10,一个内项是8,另一个内项是( )。
5
4
(2)在一个比例里,两个外项互为倒数,其中一个内项是 ,另一个内项是( )。
4
9
10÷8=
5
4
9
4
3. 4∶5=12∶15,如果内项5增加5,那么外项4应该增加多少才能使比例成立?
(4+x)∶(5+5)=12∶15
(4+x)∶10=12∶15
15(4+x)=12×10
解:设外项4应该增加x才能使比例成立。
15x=60
x=4
答:外项4应该增加4才能使比例成立。
拓展提升
一个比例的两个内项分别是0.6和1.5,两个比的比值都是 ,你能写出这个比例吗?
9
4
先写出比例结构,再根据比值把比例分成两个单独的比,把求比例的外项转化为求比的前项或后项。
解:设比例的两个外项分别是a和b。可以得到比例
a∶0.6=1.5∶b或a∶1.5=0.6∶b。
a∶0.6=
9
4
1.5∶b=
9
4
a=0.6×
9
4
a=
4
15
b=1.5÷
9
4
b=
27
8
解:设比例的两个外项分别是a和b。可以得到比例
a∶0.6=1.5∶b或a∶1.5=0.6∶b。
a∶1.5=
9
4
0.6∶b=
9
4
a=1.5×
9
4
a=
2
3
b=0.6÷
9
4
b=
27
20
∶ = ∶
20
27
2
3
1.5
0.6
答:这个比例是 或
∶ = ∶
8
27
4
15
0.6
1.5
。
课堂小结
1. 比例各部分的名称: 组成比例的四个数,叫做比例的项。两端的两项叫做比例的外项,中间的两项叫做比例的内项。
2. 比例的基本性质:在比例里,两个外项的积等于两个内项的积。这叫做比例的基本性质。
(判断两个比能否成比例的依据)
这节课你有什么收获?
