人教版六年级数学下册 5鸽巢问题 第3课时 鸽巢问题的应用 课件(共20张PPT)
文档属性
| 名称 | 人教版六年级数学下册 5鸽巢问题 第3课时 鸽巢问题的应用 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-31 00:00:00 | ||
图片预览







文档简介
(共20张PPT)
人教版数学六年级(下)
数学广角
——鸽巢问题
第3课时 鸽巢问题的应用
5
1.进一步理解“鸽巢原理”,运用“鸽巢原理”进行逆向思维,解决实际问题。
2.经历运用“鸽巢原理”解决问题的过程,体验观察猜想和实践操作的学习方法。
学习目标
【重点】“鸽巢原理”的逆运用。
【难点】能根据题意设计“鸽巢”。
课堂导入
掷骰子游戏:要保证掷出的点数至少有 2 次相同,至少应掷( )次。
想一想,掷一掷。
盒子里有同样大小的红球和蓝球各4个,要想摸出的球一定有2个同色的,至少要摸出几个球?
2
新知探究
2个同色√
只摸2个球能保证是同色的吗?
验证
任意摸出2个球,会出现三种情况
2 红
2 蓝
1红1蓝
2个同色√
2个不同色×
只摸2个球不能保证是同色的。
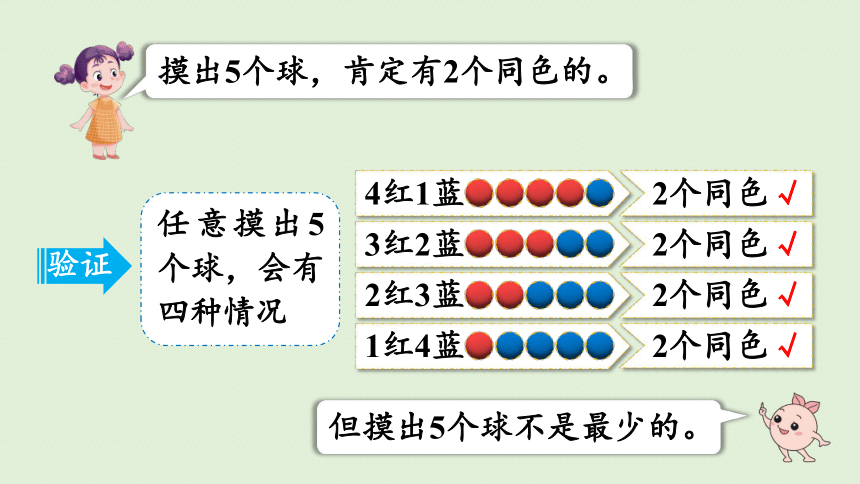
摸出5个球,肯定有2个同色的。
验证
任意摸出5个球,会有四种情况
但摸出5个球不是最少的。
2个同色√
4红1蓝
2个同色√
2个同色√
2个同色√
3红2蓝
2红3蓝
1红4蓝
摸出3个球,肯定有2个同色的。
验证
任意摸出3个球,会有四种情况
要想摸出的球一定有2个同色的,至少要摸出3个球。
2个同色√
3 红
2个同色√
2个同色√
2个同色√
2红1蓝
1红2蓝
3 蓝
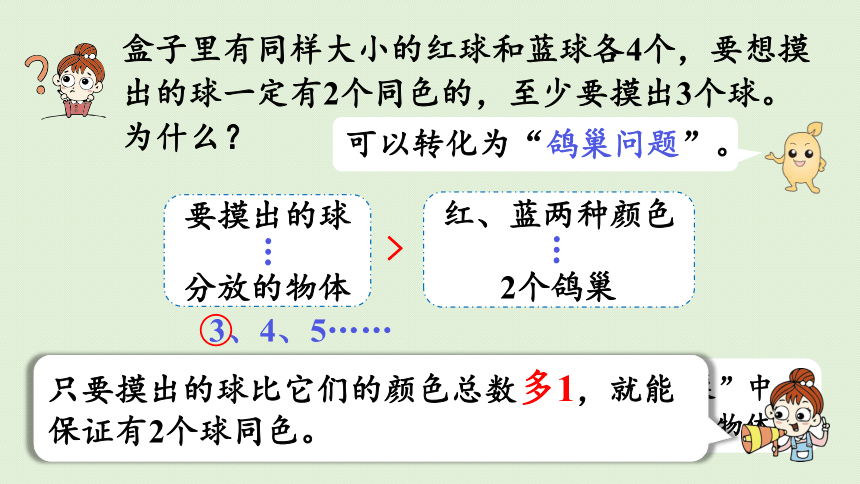
盒子里有同样大小的红球和蓝球各4个,要想摸出的球一定有2个同色的,至少要摸出3个球。为什么?
可以转化为“鸽巢问题”。
鸽巢原理(一):把多于n个物体任意放进n个“鸽巢”中(n是非0自然数),总有一个“鸽巢”中至少放进2个物体。
红、蓝两种颜色
2个鸽巢
…
要摸出的球
分放的物体
…
>
3、4、5……
只要摸出的球比它们的颜色总数多1,就能保证有2个球同色。
因为球的颜色有2种,从最不利的情况考虑,先摸出2个不同颜色的球:
,再摸出1个球:
盒子里有同样大小的红球和蓝球各4个,要想摸出的球一定有2个同色的,至少要摸出3个球。为什么?
也可以从最不利的情况考虑。
,这个球不管是什么颜色都与先摸出的其中一个球同色。
颜色数加1就是要摸出球的个数。
你发现了什么规律?
只要摸出的球
数比它们的颜色种数多1,就能保证有两个球同
色。
摸出的球数=颜色种数+1
与每种颜
色球的个数无关。
课堂练习
3
1.填一填。
2+1=3(个)
(2)盒子里有同样大小的红、黄、蓝球各10个,至少取出( )个就能保证一定有2个球颜色相同。
4
摸出的球数=颜色种数+1
3+1=4(个)
(1)盒子里有同样大小的红球和蓝球各10个,至少取出( )个就能保证一定有2个球颜色相同。
2.向东小学六年级共有367名学生,其中六(2)班有49名学生。
他们说得对吗?为什么?
六年级里至少有两人在同一天过生日。
六(2)班中至少有5人在同一个月过生日。
教材第70页“做一做”第1题
六年级里至少有两人在同一天过生日。
367÷366=1(名)……1(名)
1+1=2(名)
“六年级里至少有两人在同一天过生日”的说法正确。
一年最多有366天
鸽巢数
物体数
2.向东小学六年级共有367名学生,其中六(2)班有49名学生。
49÷12=4(名)……1(名)
4+1=5(名)
“六(2)班中至少有5人在同一个月过生日”的说法正确。
一年有12个月
鸽巢数
物体数
2.向东小学六年级共有367名学生,其中六(2)班有49名学生。
六(2)班中至少有5人在同一个月过生日。
3.把红、黄、蓝、白四种颜色的球各10个放到一个袋子里。至少取多少个球,可以保证取到两个颜色相同的球?
从最不利的原则去考虑:
假设我们每种颜色的都取一个,前4个没有同色的。
再取1个球,不论是哪一种颜色的,都一定有2个同色的。
4+1=5(个)
至少取5个球,可以保证取到两个颜色相同的球。
教材第70页“做一做”第2题
4.把红、黄、蓝、白四种颜色的球各10个放到一个袋子里。至少取多少个球,可以保证取到3个颜色相同的球?
每种颜色先取(3-1)个,再取1个就一定有3个同色的。
至少取9个球,可以保证取到3个颜色相同的球。
4×(3-1)+1 = 9(个)
4.把红、黄、蓝、白四种颜色的球各10个放到一个袋子里。至少取多少个球,可以保证取到3个颜色相同的球?4个颜色相同的呢?
每种颜色先取(4-1)个,再取1个就一定有4个同色的。
至少取13个球,可以保证取到4个颜色相同的球。
4×(4-1)+1 = 13(个)
…物体数
…鸽巢数
…至少数
你有什么发现?
4 ×( 4 - 1 ) + 1 = 13(个)
4 ×( 3 - 1 ) + 1 = 9(个)
×( - 1 ) + 1 =
4.把红、黄、蓝、白四种颜色的球各10个放到一个袋子里。至少取多少个球,可以保证取到3个颜色相同的球?4个颜色相同的呢?
×( - 1 ) + 1 =
5.李老师要将45本课外书奖励给学习进步的同学,最多分给多少名同学,才能保证至少有一名同学能分到5本书?
物体数
鸽巢数
至少数
同学数
5本书
45本课外书
(45 - 1)÷(5 - 1)= 11(名)
最多分给11名同学,才能保证至少有一名同学能分到5本书。
利用鸽巢原理解决问题的方法
课堂小结
1.分析题意,把实际问题转化成“鸽巢问题”;
2.设计“鸽巢”的具体形式;
3.运用原理得出在某个“鸽巢”里至少分放的物体个数,解决问题。
一定要注意把什么看作“鸽巢”,把什么看作“分放的物品”!
人教版数学六年级(下)
数学广角
——鸽巢问题
第3课时 鸽巢问题的应用
5
1.进一步理解“鸽巢原理”,运用“鸽巢原理”进行逆向思维,解决实际问题。
2.经历运用“鸽巢原理”解决问题的过程,体验观察猜想和实践操作的学习方法。
学习目标
【重点】“鸽巢原理”的逆运用。
【难点】能根据题意设计“鸽巢”。
课堂导入
掷骰子游戏:要保证掷出的点数至少有 2 次相同,至少应掷( )次。
想一想,掷一掷。
盒子里有同样大小的红球和蓝球各4个,要想摸出的球一定有2个同色的,至少要摸出几个球?
2
新知探究
2个同色√
只摸2个球能保证是同色的吗?
验证
任意摸出2个球,会出现三种情况
2 红
2 蓝
1红1蓝
2个同色√
2个不同色×
只摸2个球不能保证是同色的。
摸出5个球,肯定有2个同色的。
验证
任意摸出5个球,会有四种情况
但摸出5个球不是最少的。
2个同色√
4红1蓝
2个同色√
2个同色√
2个同色√
3红2蓝
2红3蓝
1红4蓝
摸出3个球,肯定有2个同色的。
验证
任意摸出3个球,会有四种情况
要想摸出的球一定有2个同色的,至少要摸出3个球。
2个同色√
3 红
2个同色√
2个同色√
2个同色√
2红1蓝
1红2蓝
3 蓝
盒子里有同样大小的红球和蓝球各4个,要想摸出的球一定有2个同色的,至少要摸出3个球。为什么?
可以转化为“鸽巢问题”。
鸽巢原理(一):把多于n个物体任意放进n个“鸽巢”中(n是非0自然数),总有一个“鸽巢”中至少放进2个物体。
红、蓝两种颜色
2个鸽巢
…
要摸出的球
分放的物体
…
>
3、4、5……
只要摸出的球比它们的颜色总数多1,就能保证有2个球同色。
因为球的颜色有2种,从最不利的情况考虑,先摸出2个不同颜色的球:
,再摸出1个球:
盒子里有同样大小的红球和蓝球各4个,要想摸出的球一定有2个同色的,至少要摸出3个球。为什么?
也可以从最不利的情况考虑。
,这个球不管是什么颜色都与先摸出的其中一个球同色。
颜色数加1就是要摸出球的个数。
你发现了什么规律?
只要摸出的球
数比它们的颜色种数多1,就能保证有两个球同
色。
摸出的球数=颜色种数+1
与每种颜
色球的个数无关。
课堂练习
3
1.填一填。
2+1=3(个)
(2)盒子里有同样大小的红、黄、蓝球各10个,至少取出( )个就能保证一定有2个球颜色相同。
4
摸出的球数=颜色种数+1
3+1=4(个)
(1)盒子里有同样大小的红球和蓝球各10个,至少取出( )个就能保证一定有2个球颜色相同。
2.向东小学六年级共有367名学生,其中六(2)班有49名学生。
他们说得对吗?为什么?
六年级里至少有两人在同一天过生日。
六(2)班中至少有5人在同一个月过生日。
教材第70页“做一做”第1题
六年级里至少有两人在同一天过生日。
367÷366=1(名)……1(名)
1+1=2(名)
“六年级里至少有两人在同一天过生日”的说法正确。
一年最多有366天
鸽巢数
物体数
2.向东小学六年级共有367名学生,其中六(2)班有49名学生。
49÷12=4(名)……1(名)
4+1=5(名)
“六(2)班中至少有5人在同一个月过生日”的说法正确。
一年有12个月
鸽巢数
物体数
2.向东小学六年级共有367名学生,其中六(2)班有49名学生。
六(2)班中至少有5人在同一个月过生日。
3.把红、黄、蓝、白四种颜色的球各10个放到一个袋子里。至少取多少个球,可以保证取到两个颜色相同的球?
从最不利的原则去考虑:
假设我们每种颜色的都取一个,前4个没有同色的。
再取1个球,不论是哪一种颜色的,都一定有2个同色的。
4+1=5(个)
至少取5个球,可以保证取到两个颜色相同的球。
教材第70页“做一做”第2题
4.把红、黄、蓝、白四种颜色的球各10个放到一个袋子里。至少取多少个球,可以保证取到3个颜色相同的球?
每种颜色先取(3-1)个,再取1个就一定有3个同色的。
至少取9个球,可以保证取到3个颜色相同的球。
4×(3-1)+1 = 9(个)
4.把红、黄、蓝、白四种颜色的球各10个放到一个袋子里。至少取多少个球,可以保证取到3个颜色相同的球?4个颜色相同的呢?
每种颜色先取(4-1)个,再取1个就一定有4个同色的。
至少取13个球,可以保证取到4个颜色相同的球。
4×(4-1)+1 = 13(个)
…物体数
…鸽巢数
…至少数
你有什么发现?
4 ×( 4 - 1 ) + 1 = 13(个)
4 ×( 3 - 1 ) + 1 = 9(个)
×( - 1 ) + 1 =
4.把红、黄、蓝、白四种颜色的球各10个放到一个袋子里。至少取多少个球,可以保证取到3个颜色相同的球?4个颜色相同的呢?
×( - 1 ) + 1 =
5.李老师要将45本课外书奖励给学习进步的同学,最多分给多少名同学,才能保证至少有一名同学能分到5本书?
物体数
鸽巢数
至少数
同学数
5本书
45本课外书
(45 - 1)÷(5 - 1)= 11(名)
最多分给11名同学,才能保证至少有一名同学能分到5本书。
利用鸽巢原理解决问题的方法
课堂小结
1.分析题意,把实际问题转化成“鸽巢问题”;
2.设计“鸽巢”的具体形式;
3.运用原理得出在某个“鸽巢”里至少分放的物体个数,解决问题。
一定要注意把什么看作“鸽巢”,把什么看作“分放的物品”!
