人教版六年级数学下册 6总复习 1数与代数 第5课时 数的运算(二)课件(共26张PPT)
文档属性
| 名称 | 人教版六年级数学下册 6总复习 1数与代数 第5课时 数的运算(二)课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 627.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-31 00:00:00 | ||
图片预览






文档简介
(共26张PPT)
人教版数学六年级(下)
整理和复习
第5课时 数的运算(二)
6
1.数与代数
复习导入
教材第78页第9题
通过计算可以解决许多实际问题,解决实际问题时有哪些主要步骤?
阅读与理解:读题,理解题意,明确已知条件和所求问题。
分析与解答:先分析数量关系,确定怎样算,再列式计算。
回顾与反思:反思解题过程,验证答案是否正确,并写出答语。
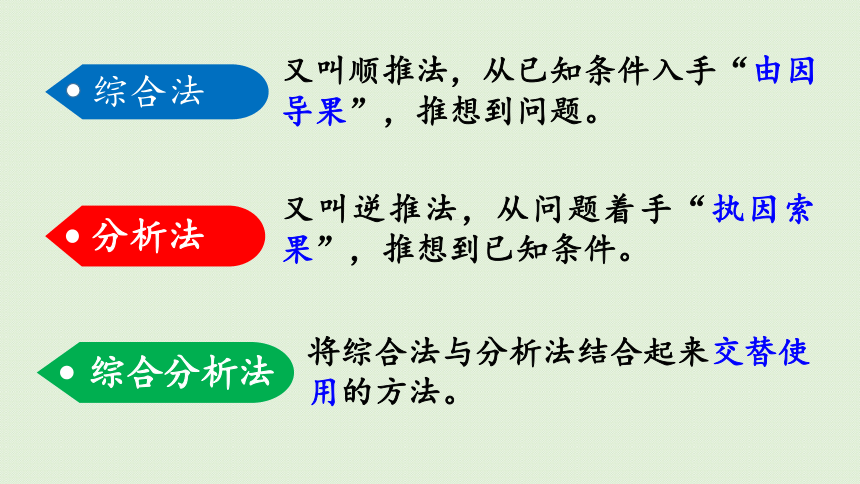
综合法
分析法
综合分析法
又叫顺推法,从已知条件入手“由因导果”,推想到问题。
又叫逆推法,从问题着手“执因索果”,推想到已知条件。
将综合法与分析法结合起来交替使用的方法。
画图可以帮助我们思考。
归纳整理
六年级举行“小发明”比赛,六(1)班同学上交32件作品,六(2)班比六(1)班多交-,两个班共交了多少件作品?
1
4
教材第78页第10题
六(1)班
六(2)班
32件
比六(1)班多-
1
4
件
先求六(2)班的,再求一共的。
32×(1+-)
14
32+
=72(件)
答:两个班共交了72件作品。
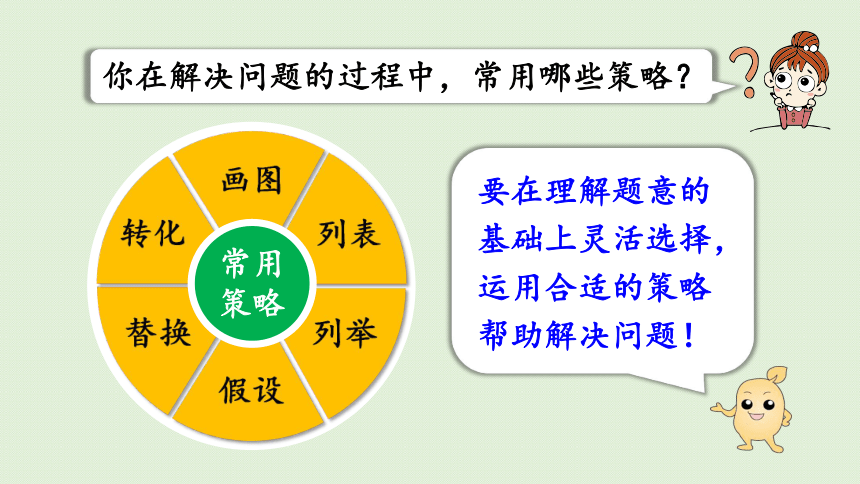
你在解决问题的过程中,常用哪些策略?
画图
列表
列举
假设
替换
转化
常用策略
要在理解题意的基础上灵活选择,运用合适的策略帮助解决问题!
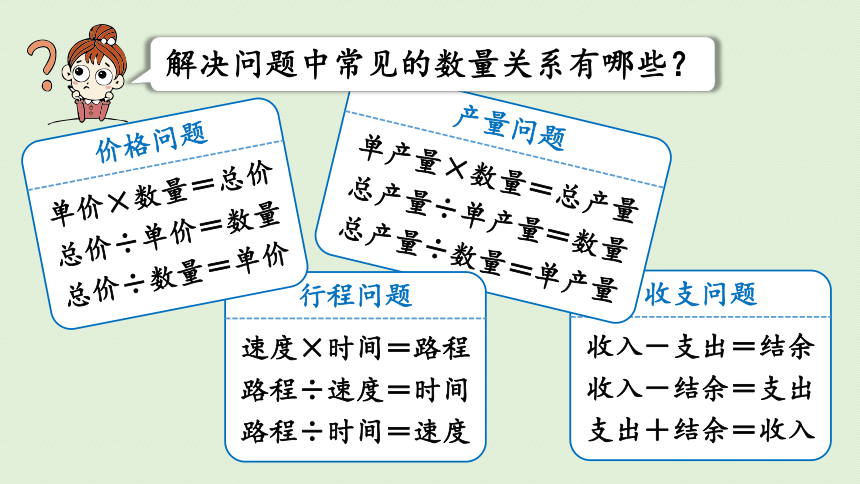
收入-支出=结余
收入-结余=支出
支出+结余=收入
收支问题
单产量×数量=总产量
总产量÷单产量=数量
总产量÷数量=单产量
产量问题
速度×时间=路程
路程÷速度=时间
路程÷时间=速度
行程问题
单价×数量=总价
总价÷单价=数量
总价÷数量=单价
价格问题
解决问题中常见的数量关系有哪些?
你遇到过哪些类型的实际问题?
平均数问题
归一问题
归总问题
行程问题
和倍问题
差倍问题
和差问题
年龄问题
分段计费问题
分数或百分数问题
工程问题
分数或百分数问题
(1)求甲数是乙数的几(百)分之几。
甲数÷乙数=甲数是乙数的几(百)分之几
(2)已知甲数是乙数的几(百)分之几,求甲数。
乙数×几(百)分之几=甲数
(3)已知甲数是乙数的几(百)分之几,求乙数。
甲数÷几(百)分之几=乙数
分数或百分数问题
(4)求甲数比乙数多(少)几(百)分之几。
两个数的差÷乙数=
甲数比乙数多(少)的几(百)分之几
(5)已知甲数比乙数多(少)几(百)分之几,求甲数。
乙数×[1±几(百)分之几]=甲数
(6)已知甲数比乙数多(少)几(百)分之几,求乙数。
甲数÷[1±几(百)分之几]=乙数
折扣问题、成数问题、纳税问题、储蓄问题都可以转化为一般的百分数问题来分析解答。
折扣问题
成数问题
储蓄问题
纳税问题
现价÷折扣=原价
现价÷原价=折扣
几成就是十分之几,也就是百分之几十。
应纳税所得额×税率=应纳税额
利息=本金×利率×存期
原价×折扣=现价
课堂练习
1.填一填。
现价÷原价=折扣
(1)一本书现价6.4元,比原价便宜1.6元。这本书是打( )折出售的。
八
6.4÷(6.4+1.6)=80%=八折
(2)用50粒种子做发芽试验,有7粒种子未发芽。这些种子的发芽率是( )。
发芽率=发芽粒数÷总粒数
(50-7)÷50=86%
86%
(3)某玩具厂上午卖出玩具1.5万个,下午卖出同样的玩具2.3万个。下午卖出的比上午卖出的多收入10.8万元,平均每个玩具卖( )元。
总数量÷总份数=平均数;
多收入的总价对应多卖出的数量。
10.8÷(2.3-1.5)
=10.8÷0.8
=13.5(元)
13.5
(4)张阿姨开着车以80千米/时的速度在一条路上行驶,前方出现限速60千米/时的标志。如果张阿姨继续保持原来的速度,那么她将受到扣( )分的处罚。
超速50%及以上,扣12分;超速20%及以上未达到50%,扣6分;超速未达到20%,扣3分。
(80-60)÷60 ≈ 33.3%
20%<33.3%<50%
要求超速百分之几就用“超过限速的部分÷限速”
6
(5)有一条3米长的彩带,先剪去全长的-,又剪去-米,这时还剩下( )米。
1
3
1
3
两次剪去的一样长吗?
53
-
第一次剪去的是全长的-,
第二次剪去的是-米,不一样长。
13
13
3-3×---=-(米)
13
13
53
2.学生夏令营组织远足,原计划3小时走完11.25 km。实际2.5小时就走完了原定路程。实际比原计划每小时多走多少千米?
教材第78页“做一做”第2题
速度=路程÷时间,分别求出实际和原计划的速度就可以求出实际比原计划每小时多走多少千米。
11.25÷2.5-11.25÷3
=4.5-3.75
=0.75(km)
答:实际比原计划每小时多走0.75 km。
3.某家具厂生产一批家具,原计划15天完成,实际上每天生产298件,这样不但提前3天完成任务,还超额生产了186件,原计划每天生产多少件?
原计划每天生产多少件
原计划的总件数
原计划的天数
÷
实际生产的件数
超额生产的件数
-
实际每天生产的
实际生产的天数
×
原计划的天数
提前的天数
-
分析法
综合法
解决问题时,一般运用“分析法”“综合法”和“综合分析法”分析数量关系。
[298×(15-3)-186]÷15
=[298×12-186]÷15
=[3576-186]÷15
=3390÷15
=226(件)
答:原计划每天生产226件。
3.某家具厂生产一批家具,原计划15天完成,实际上每天生产298件,这样不但提前3天完成任务,还超额生产了186件,原计划每天生产多少件?
4.某服装店卖一种裙子,原来每条的售价为120元,是进价的150%。现在店主计划打折促销,但要保证每条裙子的盈利不少于10元。问:折扣不能低于几折?
先求进价,用售价除以150%;再求现在的最低售价,比进价高10元;最后用现在的最低售价除以原售价求得最低折扣。
(120÷150%+10)÷120
=(80+10)÷120
=75%
=七五折
答:折扣不能低于七五折。
5.李师傅和王师傅共同加工一批零件,两人一起做,12小时就可以完成,如果让王师傅单独做,那么需要20小时完成。如果让李师傅单独做,那么需要多少小时完成?
根据“两人一起做要12小时完成”,可以求出两人合作1小时的工作量;根据“王师傅单独做要20小时”,可以求出王师傅1小时的工作量,就可以求出李师傅1小时的工作量,进而求出李师傅单独完成需要的时间。
工作时间=工作总量÷工作效率
1÷( - )
1
12
1
20
=1÷
1
30
=30(小时)
答:如果让李师傅单独做,那么需要30小时完成。
5.李师傅和王师傅共同加工一批零件,两人一起做,12小时就可以完成,如果让王师傅单独做,那么需要20小时完成。如果让李师傅单独做,那么需要多少小时完成?
6.某商店新购进两台电视机,以每台4800元的价格出售。其中一台的售价比进价高25%,另一台的售价比进价低20%。总的来看,该商店是赚钱了还是赔钱了?
其中一台的售价是进价的(1+25%),
另一台的售价是进价的(1-20%)。
先求出两台电视机的进价,
再比较两台电视机的总进价与总售价,
得出是赚钱了还是赔钱了。
总进价: 4800÷(1+25%)+4800÷(1-20%)
=4800÷1.25+4800÷0.8
=3840+6000
=9840(元)
总售价:4800×2=9600(元)
9600<9840
答:总的来看,该商店赔钱了。
6.某商店新购进两台电视机,以每台4800元的价格出售。其中一台的售价比进价高25%,另一台的售价比进价低20%。总的来看,该商店是赚钱了还是赔钱了?
7.某地医疗保险报销规定:住院医疗报销起付线为800元,起付线以上的部分报销60%。今年王大爷患病住院,医疗费共18000元。王大爷这次生病住院自己花费多少元?
用18000元减去800元,求出可报销部分的钱数;再乘60%即可求出报销的金额;总费用减去报销的金额就可以求出王大爷自己花费的金额。
18000-(18000-800)×60%
=18000-17200×60%
=18000-10320
=7680(元)
答:王大爷这次生病住院自己花费7680元。
解决本题的关键是明确800元不在报销范围之内。
7.某地医疗保险报销规定:住院医疗报销起付线为800元,起付线以上的部分报销60%。今年王大爷患病住院,医疗费共18000元。王大爷这次生病住院自己花费多少元?
两辆汽车到第二次相遇共行了三个全程。第一次相遇(第一个全程)时,从南站出发的汽车行了60千米。
8.两辆汽车同时从南、北两站相向开出。第一次在离南站60千米处相遇,之后,两车继续以原来的速度前进。各自到达对方车站后都立即返回。又在距中点北侧30千米处相遇。南、北两站相距多少千米?
两车走三个全程时,这辆汽车走了3个60千米,这时这辆汽车距中点30千米,这辆汽车如果再行30千米就一共行驶了南、北两站路程的1.5倍。
南站
北站
60千米
30千米
(60×3+30)÷1.5
=(180+30)÷1.5
=210÷1.5
=140(千米)
答:南、北两站相距140千米。
通过画图,可以让题中的条件和问题更加明朗,有利于直观地分析条件和问题之间的关系,从而解决问题。
8.两辆汽车同时从南、北两站相向开出。第一次在离南站60千米处相遇,之后,两车继续以原来的速度前进。各自到达对方车站后都立即返回。又在距中点北侧30千米处相遇。南、北两站相距多少千米?
人教版数学六年级(下)
整理和复习
第5课时 数的运算(二)
6
1.数与代数
复习导入
教材第78页第9题
通过计算可以解决许多实际问题,解决实际问题时有哪些主要步骤?
阅读与理解:读题,理解题意,明确已知条件和所求问题。
分析与解答:先分析数量关系,确定怎样算,再列式计算。
回顾与反思:反思解题过程,验证答案是否正确,并写出答语。
综合法
分析法
综合分析法
又叫顺推法,从已知条件入手“由因导果”,推想到问题。
又叫逆推法,从问题着手“执因索果”,推想到已知条件。
将综合法与分析法结合起来交替使用的方法。
画图可以帮助我们思考。
归纳整理
六年级举行“小发明”比赛,六(1)班同学上交32件作品,六(2)班比六(1)班多交-,两个班共交了多少件作品?
1
4
教材第78页第10题
六(1)班
六(2)班
32件
比六(1)班多-
1
4
件
先求六(2)班的,再求一共的。
32×(1+-)
14
32+
=72(件)
答:两个班共交了72件作品。
你在解决问题的过程中,常用哪些策略?
画图
列表
列举
假设
替换
转化
常用策略
要在理解题意的基础上灵活选择,运用合适的策略帮助解决问题!
收入-支出=结余
收入-结余=支出
支出+结余=收入
收支问题
单产量×数量=总产量
总产量÷单产量=数量
总产量÷数量=单产量
产量问题
速度×时间=路程
路程÷速度=时间
路程÷时间=速度
行程问题
单价×数量=总价
总价÷单价=数量
总价÷数量=单价
价格问题
解决问题中常见的数量关系有哪些?
你遇到过哪些类型的实际问题?
平均数问题
归一问题
归总问题
行程问题
和倍问题
差倍问题
和差问题
年龄问题
分段计费问题
分数或百分数问题
工程问题
分数或百分数问题
(1)求甲数是乙数的几(百)分之几。
甲数÷乙数=甲数是乙数的几(百)分之几
(2)已知甲数是乙数的几(百)分之几,求甲数。
乙数×几(百)分之几=甲数
(3)已知甲数是乙数的几(百)分之几,求乙数。
甲数÷几(百)分之几=乙数
分数或百分数问题
(4)求甲数比乙数多(少)几(百)分之几。
两个数的差÷乙数=
甲数比乙数多(少)的几(百)分之几
(5)已知甲数比乙数多(少)几(百)分之几,求甲数。
乙数×[1±几(百)分之几]=甲数
(6)已知甲数比乙数多(少)几(百)分之几,求乙数。
甲数÷[1±几(百)分之几]=乙数
折扣问题、成数问题、纳税问题、储蓄问题都可以转化为一般的百分数问题来分析解答。
折扣问题
成数问题
储蓄问题
纳税问题
现价÷折扣=原价
现价÷原价=折扣
几成就是十分之几,也就是百分之几十。
应纳税所得额×税率=应纳税额
利息=本金×利率×存期
原价×折扣=现价
课堂练习
1.填一填。
现价÷原价=折扣
(1)一本书现价6.4元,比原价便宜1.6元。这本书是打( )折出售的。
八
6.4÷(6.4+1.6)=80%=八折
(2)用50粒种子做发芽试验,有7粒种子未发芽。这些种子的发芽率是( )。
发芽率=发芽粒数÷总粒数
(50-7)÷50=86%
86%
(3)某玩具厂上午卖出玩具1.5万个,下午卖出同样的玩具2.3万个。下午卖出的比上午卖出的多收入10.8万元,平均每个玩具卖( )元。
总数量÷总份数=平均数;
多收入的总价对应多卖出的数量。
10.8÷(2.3-1.5)
=10.8÷0.8
=13.5(元)
13.5
(4)张阿姨开着车以80千米/时的速度在一条路上行驶,前方出现限速60千米/时的标志。如果张阿姨继续保持原来的速度,那么她将受到扣( )分的处罚。
超速50%及以上,扣12分;超速20%及以上未达到50%,扣6分;超速未达到20%,扣3分。
(80-60)÷60 ≈ 33.3%
20%<33.3%<50%
要求超速百分之几就用“超过限速的部分÷限速”
6
(5)有一条3米长的彩带,先剪去全长的-,又剪去-米,这时还剩下( )米。
1
3
1
3
两次剪去的一样长吗?
53
-
第一次剪去的是全长的-,
第二次剪去的是-米,不一样长。
13
13
3-3×---=-(米)
13
13
53
2.学生夏令营组织远足,原计划3小时走完11.25 km。实际2.5小时就走完了原定路程。实际比原计划每小时多走多少千米?
教材第78页“做一做”第2题
速度=路程÷时间,分别求出实际和原计划的速度就可以求出实际比原计划每小时多走多少千米。
11.25÷2.5-11.25÷3
=4.5-3.75
=0.75(km)
答:实际比原计划每小时多走0.75 km。
3.某家具厂生产一批家具,原计划15天完成,实际上每天生产298件,这样不但提前3天完成任务,还超额生产了186件,原计划每天生产多少件?
原计划每天生产多少件
原计划的总件数
原计划的天数
÷
实际生产的件数
超额生产的件数
-
实际每天生产的
实际生产的天数
×
原计划的天数
提前的天数
-
分析法
综合法
解决问题时,一般运用“分析法”“综合法”和“综合分析法”分析数量关系。
[298×(15-3)-186]÷15
=[298×12-186]÷15
=[3576-186]÷15
=3390÷15
=226(件)
答:原计划每天生产226件。
3.某家具厂生产一批家具,原计划15天完成,实际上每天生产298件,这样不但提前3天完成任务,还超额生产了186件,原计划每天生产多少件?
4.某服装店卖一种裙子,原来每条的售价为120元,是进价的150%。现在店主计划打折促销,但要保证每条裙子的盈利不少于10元。问:折扣不能低于几折?
先求进价,用售价除以150%;再求现在的最低售价,比进价高10元;最后用现在的最低售价除以原售价求得最低折扣。
(120÷150%+10)÷120
=(80+10)÷120
=75%
=七五折
答:折扣不能低于七五折。
5.李师傅和王师傅共同加工一批零件,两人一起做,12小时就可以完成,如果让王师傅单独做,那么需要20小时完成。如果让李师傅单独做,那么需要多少小时完成?
根据“两人一起做要12小时完成”,可以求出两人合作1小时的工作量;根据“王师傅单独做要20小时”,可以求出王师傅1小时的工作量,就可以求出李师傅1小时的工作量,进而求出李师傅单独完成需要的时间。
工作时间=工作总量÷工作效率
1÷( - )
1
12
1
20
=1÷
1
30
=30(小时)
答:如果让李师傅单独做,那么需要30小时完成。
5.李师傅和王师傅共同加工一批零件,两人一起做,12小时就可以完成,如果让王师傅单独做,那么需要20小时完成。如果让李师傅单独做,那么需要多少小时完成?
6.某商店新购进两台电视机,以每台4800元的价格出售。其中一台的售价比进价高25%,另一台的售价比进价低20%。总的来看,该商店是赚钱了还是赔钱了?
其中一台的售价是进价的(1+25%),
另一台的售价是进价的(1-20%)。
先求出两台电视机的进价,
再比较两台电视机的总进价与总售价,
得出是赚钱了还是赔钱了。
总进价: 4800÷(1+25%)+4800÷(1-20%)
=4800÷1.25+4800÷0.8
=3840+6000
=9840(元)
总售价:4800×2=9600(元)
9600<9840
答:总的来看,该商店赔钱了。
6.某商店新购进两台电视机,以每台4800元的价格出售。其中一台的售价比进价高25%,另一台的售价比进价低20%。总的来看,该商店是赚钱了还是赔钱了?
7.某地医疗保险报销规定:住院医疗报销起付线为800元,起付线以上的部分报销60%。今年王大爷患病住院,医疗费共18000元。王大爷这次生病住院自己花费多少元?
用18000元减去800元,求出可报销部分的钱数;再乘60%即可求出报销的金额;总费用减去报销的金额就可以求出王大爷自己花费的金额。
18000-(18000-800)×60%
=18000-17200×60%
=18000-10320
=7680(元)
答:王大爷这次生病住院自己花费7680元。
解决本题的关键是明确800元不在报销范围之内。
7.某地医疗保险报销规定:住院医疗报销起付线为800元,起付线以上的部分报销60%。今年王大爷患病住院,医疗费共18000元。王大爷这次生病住院自己花费多少元?
两辆汽车到第二次相遇共行了三个全程。第一次相遇(第一个全程)时,从南站出发的汽车行了60千米。
8.两辆汽车同时从南、北两站相向开出。第一次在离南站60千米处相遇,之后,两车继续以原来的速度前进。各自到达对方车站后都立即返回。又在距中点北侧30千米处相遇。南、北两站相距多少千米?
两车走三个全程时,这辆汽车走了3个60千米,这时这辆汽车距中点30千米,这辆汽车如果再行30千米就一共行驶了南、北两站路程的1.5倍。
南站
北站
60千米
30千米
(60×3+30)÷1.5
=(180+30)÷1.5
=210÷1.5
=140(千米)
答:南、北两站相距140千米。
通过画图,可以让题中的条件和问题更加明朗,有利于直观地分析条件和问题之间的关系,从而解决问题。
8.两辆汽车同时从南、北两站相向开出。第一次在离南站60千米处相遇,之后,两车继续以原来的速度前进。各自到达对方车站后都立即返回。又在距中点北侧30千米处相遇。南、北两站相距多少千米?
