人教版六年级数学下册 6总复习 2图形与几何 第2课时 平面图形的认识与测量(2)课件(共24张PPT)
文档属性
| 名称 | 人教版六年级数学下册 6总复习 2图形与几何 第2课时 平面图形的认识与测量(2)课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-31 21:04:45 | ||
图片预览




文档简介
(共24张PPT)
人教版数学六年级(下)
整理和复习
第2课时 平面图形的认识与测量(2)
6
2.图形与几何
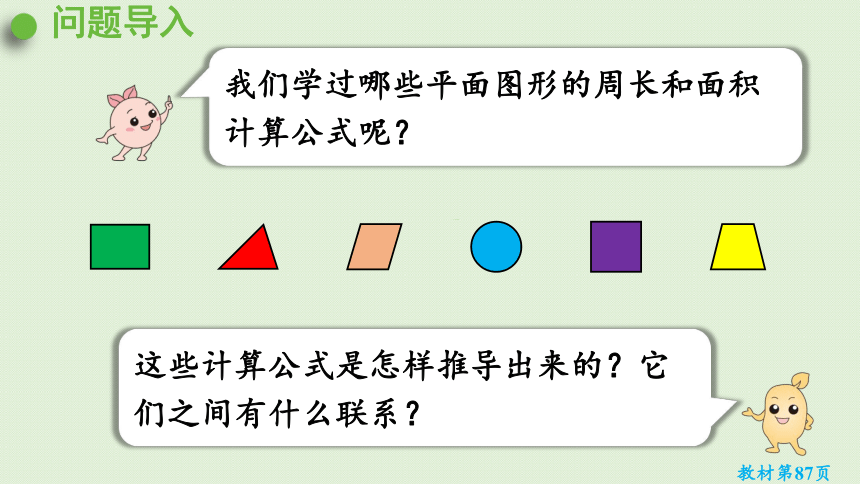
问题导入
我们学过哪些平面图形的周长和面积计算公式呢?
教材第87页
这些计算公式是怎样推导出来的?它们之间有什么联系?
a
b
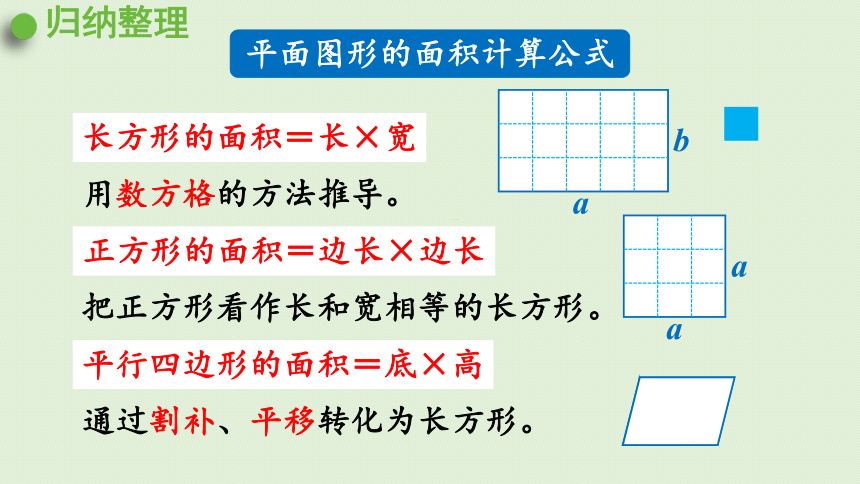
归纳整理
平面图形的面积计算公式
用数方格的方法推导。
把正方形看作长和宽相等的长方形。
a
a
通过割补、平移转化为长方形。
长方形的面积=长×宽
正方形的面积=边长×边长
平行四边形的面积=底×高
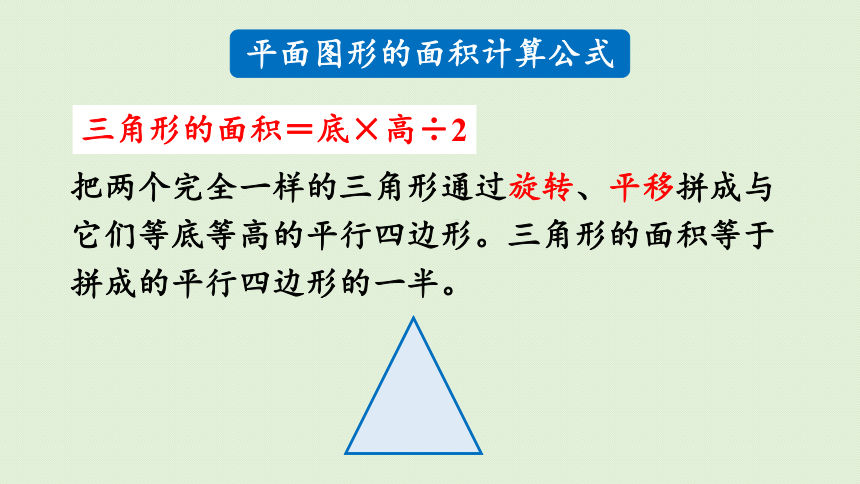
把两个完全一样的三角形通过旋转、平移拼成与它们等底等高的平行四边形。三角形的面积等于拼成的平行四边形的一半。
平面图形的面积计算公式
三角形的面积=底×高÷2
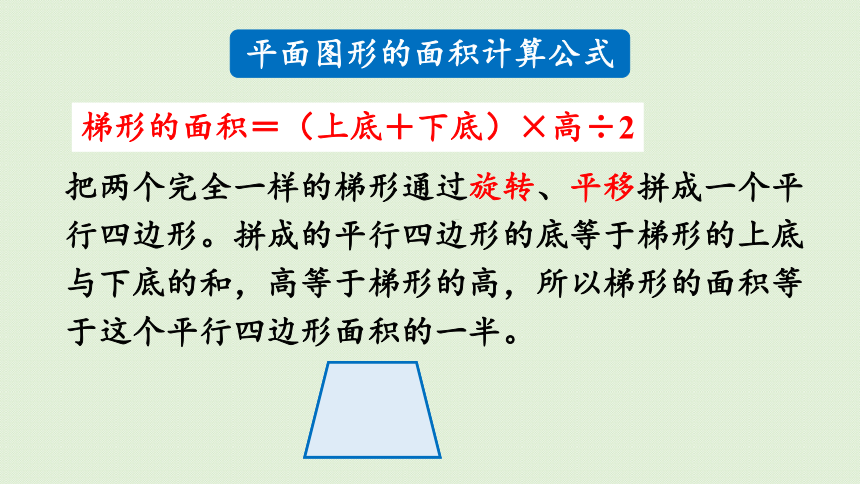
把两个完全一样的梯形通过旋转、平移拼成一个平行四边形。拼成的平行四边形的底等于梯形的上底与下底的和,高等于梯形的高,所以梯形的面积等于这个平行四边形面积的一半。
平面图形的面积计算公式
梯形的面积=(上底+下底)×高÷2
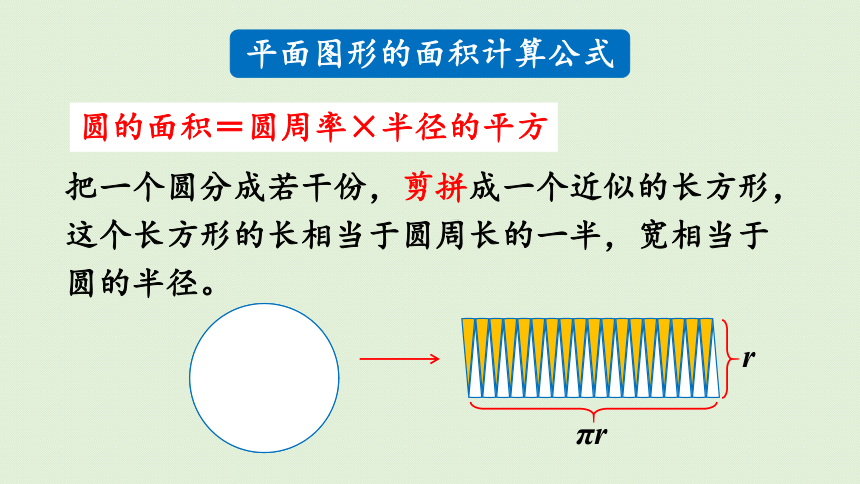
把一个圆分成若干份,剪拼成一个近似的长方形,这个长方形的长相当于圆周长的一半,宽相当于圆的半径。
平面图形的面积计算公式
圆的面积=圆周率×半径的平方
πr
r
平面图形的面积计算公式
圆的面积=圆周率×半径的平方
长方形的面积=长×宽
正方形的面积=边长×边长
平行四边形的面积=底×高
三角形的面积=底×高÷2
梯形的面积=(上底+下底)×高÷2
S=ab
S=a2
S=ah
S=ah÷2
S=(a+b)h÷2
S=πr2
平面图形的周长计算公式
圆的周长=圆周率×直径
长方形的周长=(长+宽)×2
正方形的周长=边长×4
平行四边形的周长=相邻两边的长度和×2
三角形的周长=三条边的长度和
梯形的周长=四条边的长度和
C=2(a+b)
C=4a
C=2(a+b)
C=a+b+c
C=a+b+c+d
C=πd=2πr
课堂练习
1.计算下面各图形的周长和面积。(单位:m)
教材第87页“做一做”第4题
周长:
30
40
50
30+40+50=120(m)
面积:
30×40÷2
=1200÷2
=600(m2)
1.计算下面各图形的周长和面积。(单位:m)
周长:
6×2+10.5+7.5=30(m)
面积:
(6+10.5)×6÷2
=16.5×6÷2
=49.5(m2)
6
7.5
10.5
6
a
b
h
3.14×5÷2
1.计算下面各图形的周长和面积。(单位:m)
周长:
=7.85+15
=22.85(m)
面积:
=9.8125+15
=24.8125(m2)
a
5
3
5
+5
×3
3.14×(5÷2)2÷2
+5×3
(1)如下图(单位:cm),一个长方形框架变形后成了一个平行四边形,原来这个长方形的周长是( )cm,变形后的平行四边形面积是( )cm2。
2.填一填。
26
长方形的周长:
8×4=32(cm2)
(8+5)×2=26(cm)
原来长方形的宽为5 cm。
32
8
4
5
5
平行四边形的面积:
(2)如下图的平行四边形中,阴影部分的面积是6cm2,平行四边形的底是直角三角形的3倍,空白部分的面积是( )cm2。
6×2÷4=3(cm)
4 cm
3 cm
三角形的底=面积×2÷高。
3×3=9(cm)
9 cm
9×4-6=30(cm2)
三角形的底:
平行四边形的底:
空白部分的面积:
30
(3)如下图,张大爷用24米长的栅栏靠墙围成一块梯形菜地,这块菜地的面积是( )平方米。
54
6 m
24米长的栅栏分布在梯形的上底、高和下底三个部分,已知高是6米,则上、下底的和是(24-6)米。
(24-6)×6÷2=54(平方米)
(4)在一张长24 cm、宽20 cm的长方形纸上画一个最大的圆,这个圆的周长是( )cm,面积是( )cm2;如果改画最大的半圆,这个半圆的面积( )cm2。
62.8
314
圆的周长:3.14×20=62.8(cm)
圆的面积:3.14×(20÷2)2=314(cm2)
半圆的面积:3.14×(24÷2)2÷2=226.08(cm2)
226.08
圆的直径最大为20 cm。
半圆的直径最大为24 cm。
(5)如图,在大、小两个正方形中涂色部分的面积比是3∶2,则大、小两个正方形的边长比是( ),面积比是( )。
3∶2
9∶4
a
b
b
ab÷2 3
b2÷2 2
=-
-=-
a 3
b 2
涂色部分的面积比:
根据比的基本性质:
a2 32 9
b2 22 4
-=-=-
大、小正方形的面积比:
用a、b分别表示两个正方形的边长。
3.选一选。
(1)一个平行四边形相邻的两条边分别是6 cm、4 cm,量得一条边上的高是5 cm,这个平行四边形的面积是( )cm2。
A.30 B.24 C.20 D.10
C
4 cm
6 cm
小于4 cm
4 cm
4 cm
6 cm
小于6 cm
6 cm
以4 cm为底的高是5 cm
4×5=20(cm2)
(2)一个三角形的底和高相等,如果将底减少2分米,高增加2分米,那么这个三角形的面积会( )。
A.增加 B.减少 C.不变
B
原面积:6×6÷2=18(dm2)
新面积:(6-2)×(6+2)÷2=16(dm2)
16<18,面积减少了。
假设原三角形的底和高都是6分米。
(3)如下图,用三张同样大小的正方形纸分别剪掉图中涂色部分的图形,材料的利用率( )。
A.甲最高 B.乙最高 C.丙最高 D.相同
D
甲乙丙
甲:3.14×102÷4÷102=78.5%
乙:3.14×(10÷2)2÷102=78.5%
丙:3.14×(10÷2÷2)2×4÷102=78.5%
假设正方形的边长是10厘米。
(36+52)×42÷2÷1.5
=88×42÷2÷1.5
=1848÷1.5
=1232(棵)
答:这个果园最多可种1232棵果树。
4.一个梯形果园,上底是36米,下底是52米,高是42米。平均每棵果树占地1.5平方米,这个果园最多可种多少棵果树?
梯形的面积=(上底+下底)×高÷2
5.一个圆形池塘,直径为28 m,环绕池塘修建一条宽为2 m的道路,这条道路的面积是多少平方米?外沿周长是多少米?
3.14×[(28÷2+2)2-(28÷2)2]
=3.14×[162-142]
=3.14×60
=188.4(平方米)
O
28 m
2 m
圆环的面积:S=π(R2-r2)
2×3.14×(28÷2+2)
=2×3.14×16
=100.48(米)
答:这条道路的面积是188.4平方米,外沿周长是100.48米。
O
外沿的周长:C=2πR
5.一个圆形池塘,直径为28 m,环绕池塘修建一条宽为2 m的道路,这条道路的面积是多少平方米?外沿周长是多少米?
28 m
2 m
=3.14×27+3.14×2
=3.14×29
=91.06(平方米)
答:这只羊能吃到草的面积是91.06平方米。
6.草地上有一间房子,占地形状是边长4米的正方形。一只羊被拴在房子的外墙角处,已知栓羊的绳子长6米,这只羊能吃到草的面积是多少平方米?
2 m
6 m
3.14×62×-
3
4
+3.14×(6-4)2×-
1
2
如图,羊能吃到草的面积由三个扇形组成。
答:x的值是11.4。
7.已知下图中两块阴影部分的面积相等,求x的值。
扇形面积:3.14×102÷4=78.5(cm2)
10 cm
O
扇形面积减三角形面积
梯形面积减扇形面积
x cm
(10+x)×10÷2-78.5=78.5-50
三角形面积:10×10÷2=50(cm2)
(10+x)×10÷2=107
10+x=21.4
x=11.4
人教版数学六年级(下)
整理和复习
第2课时 平面图形的认识与测量(2)
6
2.图形与几何
问题导入
我们学过哪些平面图形的周长和面积计算公式呢?
教材第87页
这些计算公式是怎样推导出来的?它们之间有什么联系?
a
b
归纳整理
平面图形的面积计算公式
用数方格的方法推导。
把正方形看作长和宽相等的长方形。
a
a
通过割补、平移转化为长方形。
长方形的面积=长×宽
正方形的面积=边长×边长
平行四边形的面积=底×高
把两个完全一样的三角形通过旋转、平移拼成与它们等底等高的平行四边形。三角形的面积等于拼成的平行四边形的一半。
平面图形的面积计算公式
三角形的面积=底×高÷2
把两个完全一样的梯形通过旋转、平移拼成一个平行四边形。拼成的平行四边形的底等于梯形的上底与下底的和,高等于梯形的高,所以梯形的面积等于这个平行四边形面积的一半。
平面图形的面积计算公式
梯形的面积=(上底+下底)×高÷2
把一个圆分成若干份,剪拼成一个近似的长方形,这个长方形的长相当于圆周长的一半,宽相当于圆的半径。
平面图形的面积计算公式
圆的面积=圆周率×半径的平方
πr
r
平面图形的面积计算公式
圆的面积=圆周率×半径的平方
长方形的面积=长×宽
正方形的面积=边长×边长
平行四边形的面积=底×高
三角形的面积=底×高÷2
梯形的面积=(上底+下底)×高÷2
S=ab
S=a2
S=ah
S=ah÷2
S=(a+b)h÷2
S=πr2
平面图形的周长计算公式
圆的周长=圆周率×直径
长方形的周长=(长+宽)×2
正方形的周长=边长×4
平行四边形的周长=相邻两边的长度和×2
三角形的周长=三条边的长度和
梯形的周长=四条边的长度和
C=2(a+b)
C=4a
C=2(a+b)
C=a+b+c
C=a+b+c+d
C=πd=2πr
课堂练习
1.计算下面各图形的周长和面积。(单位:m)
教材第87页“做一做”第4题
周长:
30
40
50
30+40+50=120(m)
面积:
30×40÷2
=1200÷2
=600(m2)
1.计算下面各图形的周长和面积。(单位:m)
周长:
6×2+10.5+7.5=30(m)
面积:
(6+10.5)×6÷2
=16.5×6÷2
=49.5(m2)
6
7.5
10.5
6
a
b
h
3.14×5÷2
1.计算下面各图形的周长和面积。(单位:m)
周长:
=7.85+15
=22.85(m)
面积:
=9.8125+15
=24.8125(m2)
a
5
3
5
+5
×3
3.14×(5÷2)2÷2
+5×3
(1)如下图(单位:cm),一个长方形框架变形后成了一个平行四边形,原来这个长方形的周长是( )cm,变形后的平行四边形面积是( )cm2。
2.填一填。
26
长方形的周长:
8×4=32(cm2)
(8+5)×2=26(cm)
原来长方形的宽为5 cm。
32
8
4
5
5
平行四边形的面积:
(2)如下图的平行四边形中,阴影部分的面积是6cm2,平行四边形的底是直角三角形的3倍,空白部分的面积是( )cm2。
6×2÷4=3(cm)
4 cm
3 cm
三角形的底=面积×2÷高。
3×3=9(cm)
9 cm
9×4-6=30(cm2)
三角形的底:
平行四边形的底:
空白部分的面积:
30
(3)如下图,张大爷用24米长的栅栏靠墙围成一块梯形菜地,这块菜地的面积是( )平方米。
54
6 m
24米长的栅栏分布在梯形的上底、高和下底三个部分,已知高是6米,则上、下底的和是(24-6)米。
(24-6)×6÷2=54(平方米)
(4)在一张长24 cm、宽20 cm的长方形纸上画一个最大的圆,这个圆的周长是( )cm,面积是( )cm2;如果改画最大的半圆,这个半圆的面积( )cm2。
62.8
314
圆的周长:3.14×20=62.8(cm)
圆的面积:3.14×(20÷2)2=314(cm2)
半圆的面积:3.14×(24÷2)2÷2=226.08(cm2)
226.08
圆的直径最大为20 cm。
半圆的直径最大为24 cm。
(5)如图,在大、小两个正方形中涂色部分的面积比是3∶2,则大、小两个正方形的边长比是( ),面积比是( )。
3∶2
9∶4
a
b
b
ab÷2 3
b2÷2 2
=-
-=-
a 3
b 2
涂色部分的面积比:
根据比的基本性质:
a2 32 9
b2 22 4
-=-=-
大、小正方形的面积比:
用a、b分别表示两个正方形的边长。
3.选一选。
(1)一个平行四边形相邻的两条边分别是6 cm、4 cm,量得一条边上的高是5 cm,这个平行四边形的面积是( )cm2。
A.30 B.24 C.20 D.10
C
4 cm
6 cm
小于4 cm
4 cm
4 cm
6 cm
小于6 cm
6 cm
以4 cm为底的高是5 cm
4×5=20(cm2)
(2)一个三角形的底和高相等,如果将底减少2分米,高增加2分米,那么这个三角形的面积会( )。
A.增加 B.减少 C.不变
B
原面积:6×6÷2=18(dm2)
新面积:(6-2)×(6+2)÷2=16(dm2)
16<18,面积减少了。
假设原三角形的底和高都是6分米。
(3)如下图,用三张同样大小的正方形纸分别剪掉图中涂色部分的图形,材料的利用率( )。
A.甲最高 B.乙最高 C.丙最高 D.相同
D
甲乙丙
甲:3.14×102÷4÷102=78.5%
乙:3.14×(10÷2)2÷102=78.5%
丙:3.14×(10÷2÷2)2×4÷102=78.5%
假设正方形的边长是10厘米。
(36+52)×42÷2÷1.5
=88×42÷2÷1.5
=1848÷1.5
=1232(棵)
答:这个果园最多可种1232棵果树。
4.一个梯形果园,上底是36米,下底是52米,高是42米。平均每棵果树占地1.5平方米,这个果园最多可种多少棵果树?
梯形的面积=(上底+下底)×高÷2
5.一个圆形池塘,直径为28 m,环绕池塘修建一条宽为2 m的道路,这条道路的面积是多少平方米?外沿周长是多少米?
3.14×[(28÷2+2)2-(28÷2)2]
=3.14×[162-142]
=3.14×60
=188.4(平方米)
O
28 m
2 m
圆环的面积:S=π(R2-r2)
2×3.14×(28÷2+2)
=2×3.14×16
=100.48(米)
答:这条道路的面积是188.4平方米,外沿周长是100.48米。
O
外沿的周长:C=2πR
5.一个圆形池塘,直径为28 m,环绕池塘修建一条宽为2 m的道路,这条道路的面积是多少平方米?外沿周长是多少米?
28 m
2 m
=3.14×27+3.14×2
=3.14×29
=91.06(平方米)
答:这只羊能吃到草的面积是91.06平方米。
6.草地上有一间房子,占地形状是边长4米的正方形。一只羊被拴在房子的外墙角处,已知栓羊的绳子长6米,这只羊能吃到草的面积是多少平方米?
2 m
6 m
3.14×62×-
3
4
+3.14×(6-4)2×-
1
2
如图,羊能吃到草的面积由三个扇形组成。
答:x的值是11.4。
7.已知下图中两块阴影部分的面积相等,求x的值。
扇形面积:3.14×102÷4=78.5(cm2)
10 cm
O
扇形面积减三角形面积
梯形面积减扇形面积
x cm
(10+x)×10÷2-78.5=78.5-50
三角形面积:10×10÷2=50(cm2)
(10+x)×10÷2=107
10+x=21.4
x=11.4
