人教版六年级数学下册 6总复习 2图形与几何 第3课时 立体图形的认识与测量 (课件共23张PPT)
文档属性
| 名称 | 人教版六年级数学下册 6总复习 2图形与几何 第3课时 立体图形的认识与测量 (课件共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-31 00:00:00 | ||
图片预览



文档简介
(共23张PPT)
人教版数学六年级(下)
整理和复习
第3课时 立体图形的认识与测量
6
2.图形与几何
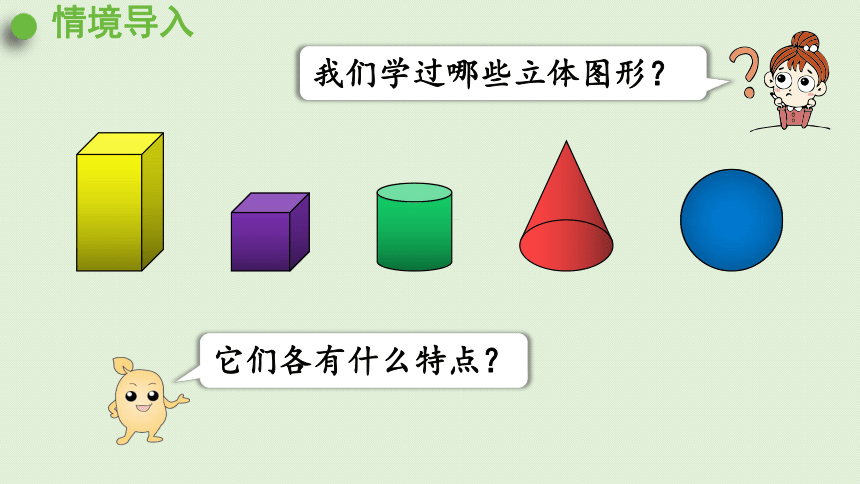
情境导入
我们学过哪些立体图形?
它们各有什么特点?
归纳整理
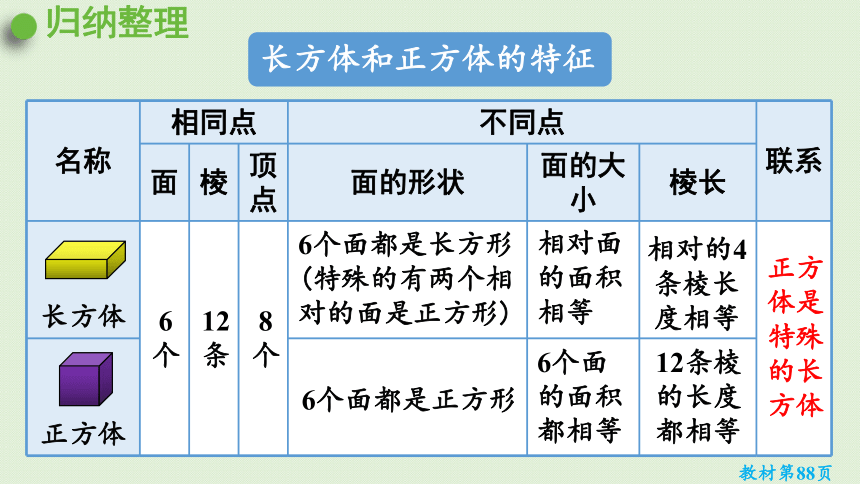
长方体和正方体的特征
名称 相同点 不同点 联系
面 棱 顶点 面的形状 面的大小 棱长 长方体
正方体
6个
12条
8个
6个面都是长方形(特殊的有两个相对的面是正方形)
6个面都是正方形
相对面的面积相等
6个面的面积都相等
相对的4条棱长度相等
12条棱的长度都相等
正方体是特殊的长方体
教材第88页
圆柱和圆锥的特征
名称 特征
圆柱
圆锥
有3个面:上、下底面是相等的两个圆,侧面是曲面。
有2个面:底面是圆,侧面是曲面。
两个底面之间的距离叫做高,有无数条长度相等的高。
顶点到底面圆心的距离叫做高,只有一条高。
侧面沿高剪开,展开后是长方形(正方形)。
侧面展开后可以得到一个扇形。
由长方形(正方形)的一边为轴旋转一周可以形成。
由直角三角形的一条直角边为轴旋转一周可以形成。
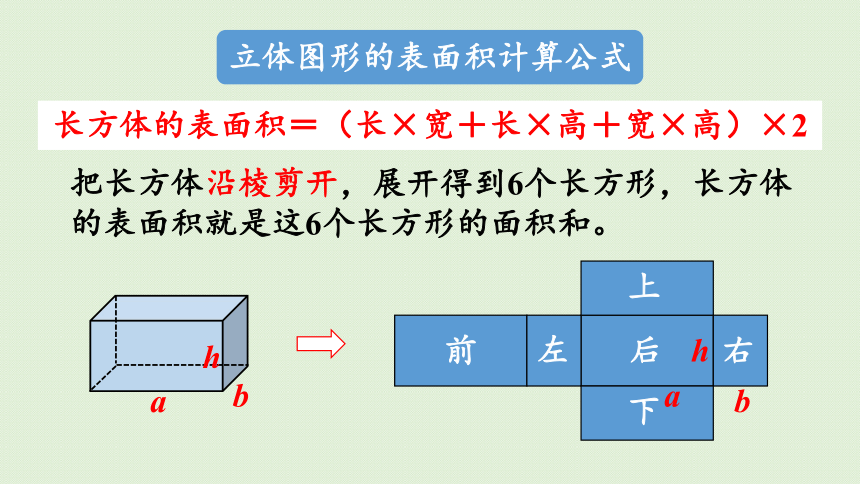
立体图形的表面积计算公式
把长方体沿棱剪开,展开得到6个长方形,长方体的表面积就是这6个长方形的面积和。
长方体的表面积=(长×宽+长×高+宽×高)×2
a
b
h
a
b
h
前
后
左
右
上
下
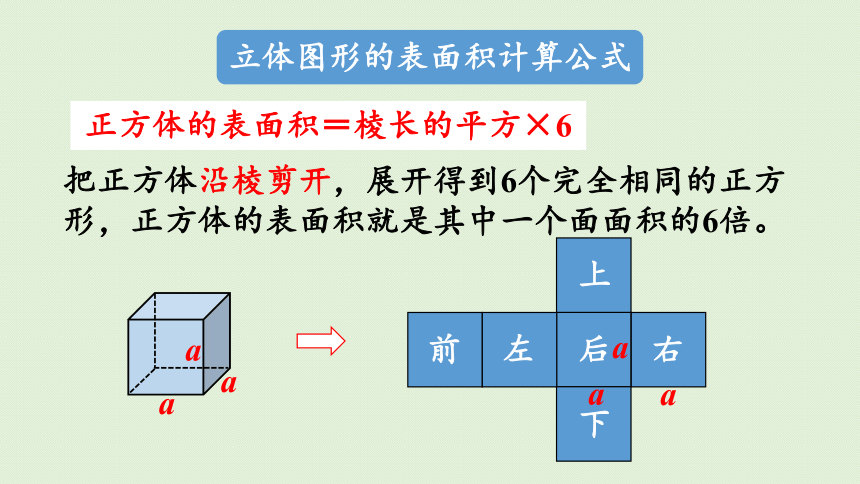
立体图形的表面积计算公式
把正方体沿棱剪开,展开得到6个完全相同的正方形,正方体的表面积就是其中一个面面积的6倍。
正方体的表面积=棱长的平方×6
a
a
a
a
前
后
左
右
上
下
a
a
立体图形的表面积计算公式
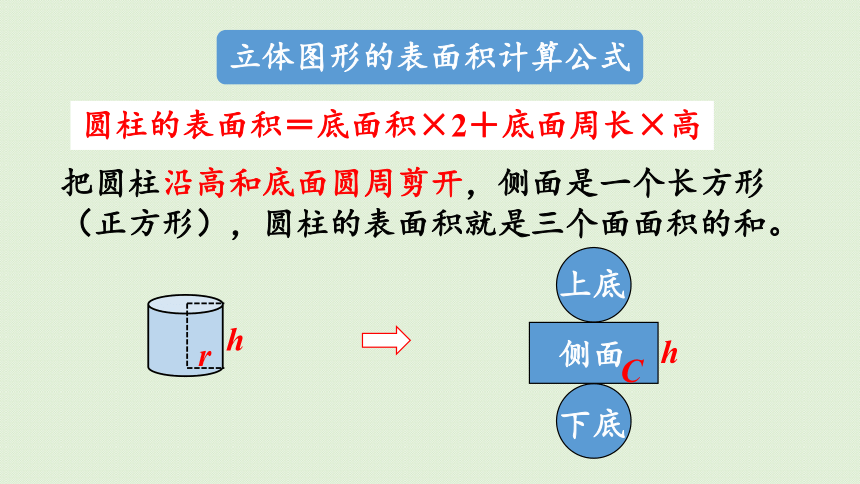
把圆柱沿高和底面圆周剪开,侧面是一个长方形(正方形),圆柱的表面积就是三个面面积的和。
圆柱的表面积=底面积×2+底面周长×高
r
h
C
侧面
上底
下底
h
立体图形的表面积计算公式
圆柱的表面积=底面积×2+底面周长×高
长方体的表面积=(长×宽+长×高+宽×高)×2
正方体的表面积=棱长的平方×6
圆柱的侧面积=底面周长×高
S=2(ab+ah+bh)
S=6a2
S侧=Ch=πdh=2πrh
S=S侧+2S底=2πrh+2πr2
立体图形的体积计算公式
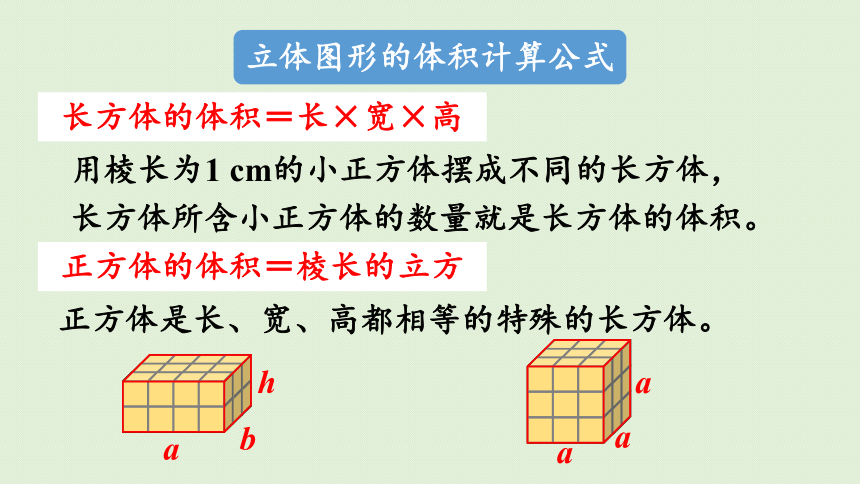
用棱长为1 cm的小正方体摆成不同的长方体,长方体所含小正方体的数量就是长方体的体积。
长方体的体积=长×宽×高
a
b
h
正方体是长、宽、高都相等的特殊的长方体。
正方体的体积=棱长的立方
a
a
a
立体图形的体积计算公式
把圆柱沿底面直径切成若干等份,可以拼成一个近似的长方体,圆柱的底面积等于长方体的底面积,圆柱的高等于长方体的高。
圆柱的体积=底面积×高
立体图形的体积计算公式
把圆锥形容器里的沙子倒入与它等底、等高的圆柱形容器内,3次才能倒满。
圆锥的体积=与圆锥等底、等高的圆柱的体积×-
13
长方体的体积=长×宽×高
正方体的体积=棱长的立方
圆柱的体积=圆周率×半径的平方×高
V=abh
V=a3
V=πr2h
立体图形的体积计算公式
圆锥体积=底面积×高×-
13
V=-S底h=-πr2h
13
13
长方体、正方体、圆柱的体积:V=S底h
课堂练习
1.判断对错,对的画“√”,错的画“×”。
绕着宽所在的直线为轴旋转一周也可以形成圆柱。
(1)长方形只有绕着长所在的直线为轴旋转一周才能形成圆柱。 ( )
(2)任意一个三角形绕它的一条边所在的直线为轴旋转都能形成圆锥。 ( )
(3)体积相等的两个长方体的底面积一定相等。( )
直角三角形绕着直角边所在的直线旋转才能形成圆锥。
×
×
体积是底面积和高的积,高不确定,底面积不一定相等。
×
2.怎样量出一个马铃薯的体积?
在容器中装满水,把不规则物体完全浸入水中,溢出水的体积就是不规则物体的体积。
求不规则物体体积的的方法:
教材第88页“做一做”第1题
在粗细均匀的容器中倒入一定量的水,把不规则物体完全浸入水中,上升的水的体积就是不规则物体的体积。
利用体积不变的特征,把不规则物体转化成规则物体再进行计算。
溢出法
升高法
转化法
上升的水的体积就是马铃薯的体积。
用“底面积×上升的高度”来计算。
2.怎样量出一个马铃薯的体积?
正面
3.在方格纸上分别画出从不同方向看到左边立体图形的形状图。
左面
上面
从不同位置观察同一个立体图形,所看到的形状一般是不同的。
教材第88页“做一做”第2题
4.小明用一根铁丝做成一个正方体框架。已知这个正方体框架的一个面的面积是49平方厘米,这根铁丝至少长( )厘米。
84
正方体的每个面都是正方形,因为49=72,所以正方体的棱长为7厘米,铁丝的长度也就是12条棱的长度和,即12×7=84(厘米)。
5.如图是由一些棱长为1厘米的小正方体摆成的,它的表面积是( )平方厘米;至少添加( )个这样的小正方体能成为一个大长方体。
22
这个物体的表面由22个正方形围成,每个正方形的面积是1×1=1(平方厘米),所以表面积是20×1=1(平方厘米)。
求表面积可以数一数表面有几个正方形。
5.如图是由一些棱长为1厘米的小正方体摆成的,它的表面积是( )平方厘米;至少添加( )个这样的小正方体能成为一个大长方体。
7
拼成的大长方体的长至少是3厘米,宽至少是2厘米,高至少是2厘米,因此一共需要3×2×2=12(个)小正方体,已有5个,至少添加12-5=7(个)。
22
先思考拼成的大长方体一共需要多少个小正方体。
6.一个棱长是10 cm的正方体,是由两个同样大小的长方体拼成的,原来一个长方体的表面积是( )cm2,体积是( )cm3。
10 cm
10 cm
10 cm
5 cm
10÷2=5(cm)
长方体的长:
表面积:
5×10×4+10×10×2
=200+200
=400(cm2)
体积:
5×10×10=500(cm3)
400
500
7.一个长方体的表面积是184 cm2,底面积是20 cm2,底面周长是18 cm,这个长方体的体积是( )cm3。
160
20 cm2
20 cm2
184-20×2=144(cm2)
144 cm2
cm
侧面积=表面积-底面积×2
144÷18=8(cm)
高=侧面积÷底面周长
20×8=160(cm3)
体积=底面积×高
18 cm
8.如下图,一个圆锥的高是3 cm,沿着它的高平均切成两部分,表面积就增加12 cm2,原来圆锥的底面直径是( )cm。
4
增加的部分是两个相同的三角形,增加部分的面积=底面直径×高。
12÷3=4(cm)
9.一块圆锥形橡皮泥,底面积是12平方厘米,高是6厘米,如果把它捏成同样高的一个圆柱,那么该圆柱的底面积是多少平方厘米?
圆锥体积=底面积×高×-
13
12×6×-=24(立方厘米)
13
圆柱的底面积=体积÷高
24÷6=4(平方厘米)
圆锥变成圆柱的过程中,体积不变。
答:该圆柱的底面积是4平方厘米。
人教版数学六年级(下)
整理和复习
第3课时 立体图形的认识与测量
6
2.图形与几何
情境导入
我们学过哪些立体图形?
它们各有什么特点?
归纳整理
长方体和正方体的特征
名称 相同点 不同点 联系
面 棱 顶点 面的形状 面的大小 棱长 长方体
正方体
6个
12条
8个
6个面都是长方形(特殊的有两个相对的面是正方形)
6个面都是正方形
相对面的面积相等
6个面的面积都相等
相对的4条棱长度相等
12条棱的长度都相等
正方体是特殊的长方体
教材第88页
圆柱和圆锥的特征
名称 特征
圆柱
圆锥
有3个面:上、下底面是相等的两个圆,侧面是曲面。
有2个面:底面是圆,侧面是曲面。
两个底面之间的距离叫做高,有无数条长度相等的高。
顶点到底面圆心的距离叫做高,只有一条高。
侧面沿高剪开,展开后是长方形(正方形)。
侧面展开后可以得到一个扇形。
由长方形(正方形)的一边为轴旋转一周可以形成。
由直角三角形的一条直角边为轴旋转一周可以形成。
立体图形的表面积计算公式
把长方体沿棱剪开,展开得到6个长方形,长方体的表面积就是这6个长方形的面积和。
长方体的表面积=(长×宽+长×高+宽×高)×2
a
b
h
a
b
h
前
后
左
右
上
下
立体图形的表面积计算公式
把正方体沿棱剪开,展开得到6个完全相同的正方形,正方体的表面积就是其中一个面面积的6倍。
正方体的表面积=棱长的平方×6
a
a
a
a
前
后
左
右
上
下
a
a
立体图形的表面积计算公式
把圆柱沿高和底面圆周剪开,侧面是一个长方形(正方形),圆柱的表面积就是三个面面积的和。
圆柱的表面积=底面积×2+底面周长×高
r
h
C
侧面
上底
下底
h
立体图形的表面积计算公式
圆柱的表面积=底面积×2+底面周长×高
长方体的表面积=(长×宽+长×高+宽×高)×2
正方体的表面积=棱长的平方×6
圆柱的侧面积=底面周长×高
S=2(ab+ah+bh)
S=6a2
S侧=Ch=πdh=2πrh
S=S侧+2S底=2πrh+2πr2
立体图形的体积计算公式
用棱长为1 cm的小正方体摆成不同的长方体,长方体所含小正方体的数量就是长方体的体积。
长方体的体积=长×宽×高
a
b
h
正方体是长、宽、高都相等的特殊的长方体。
正方体的体积=棱长的立方
a
a
a
立体图形的体积计算公式
把圆柱沿底面直径切成若干等份,可以拼成一个近似的长方体,圆柱的底面积等于长方体的底面积,圆柱的高等于长方体的高。
圆柱的体积=底面积×高
立体图形的体积计算公式
把圆锥形容器里的沙子倒入与它等底、等高的圆柱形容器内,3次才能倒满。
圆锥的体积=与圆锥等底、等高的圆柱的体积×-
13
长方体的体积=长×宽×高
正方体的体积=棱长的立方
圆柱的体积=圆周率×半径的平方×高
V=abh
V=a3
V=πr2h
立体图形的体积计算公式
圆锥体积=底面积×高×-
13
V=-S底h=-πr2h
13
13
长方体、正方体、圆柱的体积:V=S底h
课堂练习
1.判断对错,对的画“√”,错的画“×”。
绕着宽所在的直线为轴旋转一周也可以形成圆柱。
(1)长方形只有绕着长所在的直线为轴旋转一周才能形成圆柱。 ( )
(2)任意一个三角形绕它的一条边所在的直线为轴旋转都能形成圆锥。 ( )
(3)体积相等的两个长方体的底面积一定相等。( )
直角三角形绕着直角边所在的直线旋转才能形成圆锥。
×
×
体积是底面积和高的积,高不确定,底面积不一定相等。
×
2.怎样量出一个马铃薯的体积?
在容器中装满水,把不规则物体完全浸入水中,溢出水的体积就是不规则物体的体积。
求不规则物体体积的的方法:
教材第88页“做一做”第1题
在粗细均匀的容器中倒入一定量的水,把不规则物体完全浸入水中,上升的水的体积就是不规则物体的体积。
利用体积不变的特征,把不规则物体转化成规则物体再进行计算。
溢出法
升高法
转化法
上升的水的体积就是马铃薯的体积。
用“底面积×上升的高度”来计算。
2.怎样量出一个马铃薯的体积?
正面
3.在方格纸上分别画出从不同方向看到左边立体图形的形状图。
左面
上面
从不同位置观察同一个立体图形,所看到的形状一般是不同的。
教材第88页“做一做”第2题
4.小明用一根铁丝做成一个正方体框架。已知这个正方体框架的一个面的面积是49平方厘米,这根铁丝至少长( )厘米。
84
正方体的每个面都是正方形,因为49=72,所以正方体的棱长为7厘米,铁丝的长度也就是12条棱的长度和,即12×7=84(厘米)。
5.如图是由一些棱长为1厘米的小正方体摆成的,它的表面积是( )平方厘米;至少添加( )个这样的小正方体能成为一个大长方体。
22
这个物体的表面由22个正方形围成,每个正方形的面积是1×1=1(平方厘米),所以表面积是20×1=1(平方厘米)。
求表面积可以数一数表面有几个正方形。
5.如图是由一些棱长为1厘米的小正方体摆成的,它的表面积是( )平方厘米;至少添加( )个这样的小正方体能成为一个大长方体。
7
拼成的大长方体的长至少是3厘米,宽至少是2厘米,高至少是2厘米,因此一共需要3×2×2=12(个)小正方体,已有5个,至少添加12-5=7(个)。
22
先思考拼成的大长方体一共需要多少个小正方体。
6.一个棱长是10 cm的正方体,是由两个同样大小的长方体拼成的,原来一个长方体的表面积是( )cm2,体积是( )cm3。
10 cm
10 cm
10 cm
5 cm
10÷2=5(cm)
长方体的长:
表面积:
5×10×4+10×10×2
=200+200
=400(cm2)
体积:
5×10×10=500(cm3)
400
500
7.一个长方体的表面积是184 cm2,底面积是20 cm2,底面周长是18 cm,这个长方体的体积是( )cm3。
160
20 cm2
20 cm2
184-20×2=144(cm2)
144 cm2
cm
侧面积=表面积-底面积×2
144÷18=8(cm)
高=侧面积÷底面周长
20×8=160(cm3)
体积=底面积×高
18 cm
8.如下图,一个圆锥的高是3 cm,沿着它的高平均切成两部分,表面积就增加12 cm2,原来圆锥的底面直径是( )cm。
4
增加的部分是两个相同的三角形,增加部分的面积=底面直径×高。
12÷3=4(cm)
9.一块圆锥形橡皮泥,底面积是12平方厘米,高是6厘米,如果把它捏成同样高的一个圆柱,那么该圆柱的底面积是多少平方厘米?
圆锥体积=底面积×高×-
13
12×6×-=24(立方厘米)
13
圆柱的底面积=体积÷高
24÷6=4(平方厘米)
圆锥变成圆柱的过程中,体积不变。
答:该圆柱的底面积是4平方厘米。
