人教版六年级数学下册 6总复习 2图形与几何 第4课时 图形的运动 课件(共19张PPT)
文档属性
| 名称 | 人教版六年级数学下册 6总复习 2图形与几何 第4课时 图形的运动 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 792.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-31 21:05:55 | ||
图片预览





文档简介
(共19张PPT)
人教版数学六年级(下)
整理和复习
第4课时 图形的运动
6
2.图形与几何
问题导入
我们学过哪些关于图形的运动的知识?
教材第92页
平移
旋转
放大
缩小
轴对称
平移、旋转和轴对称不改变图形的形状和大小。
图形的放大和缩小只改变图形的大小不改变形状。
哪些运动不改变图形的形状和大小?
哪些运动只改变图形的大小,而不改变形状?
归纳整理
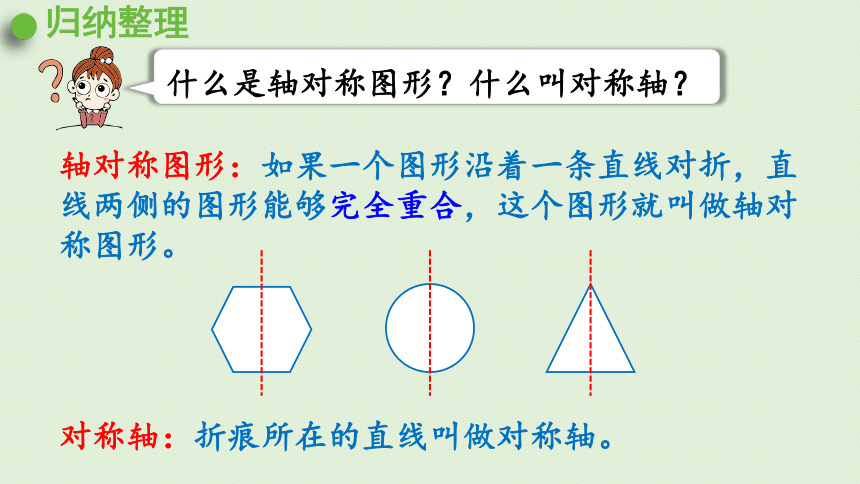
什么是轴对称图形?什么叫对称轴?
轴对称图形:如果一个图形沿着一条直线对折,直线两侧的图形能够完全重合,这个图形就叫做轴对称图形。
对称轴:折痕所在的直线叫做对称轴。
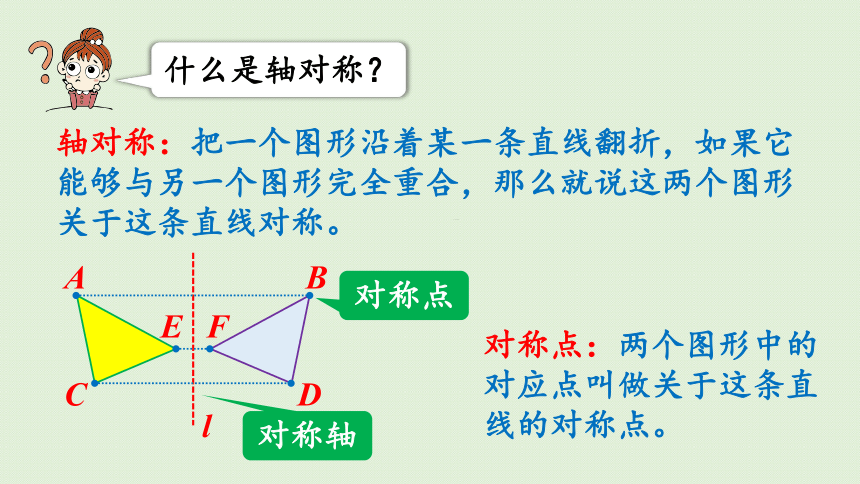
什么是轴对称?
轴对称:把一个图形沿着某一条直线翻折,如果它能够与另一个图形完全重合,那么就说这两个图形关于这条直线对称。
A
B
C
D
E
F
l
对称点
对称轴
对称点:两个图形中的对应点叫做关于这条直线的对称点。
小组交流:回忆平移的相关知识,完成下表。
图形的平移
意义
要素
特点
画法
在同一平面内,将一个图形沿一直线移动一定的距离,这样的图形运动叫做平移。
平移的方向、平移的距离。
只改变图形的位置,不改变图形的形状、大小及方向。
先找出图形的关键点,再按要求平移相应的距离,最后把这些点顺次连接起来。
小组交流:回忆旋转的相关知识,完成下表。
图形的旋转
意义
要素
特点
画法
在平面内,将一个图形绕一个点按某个方向转动一个角度,这样的图形运动叫做旋转。
旋转中心、旋转方向、旋转角度。
图形的位置、方向都改变了,但形状和大小都不变。
先找准旋转中心,然后确定旋转的方向和旋转的角度,再分别旋转各边,最后画出各边的对应边。
将一个图形按一定的比放大或缩小,原图形与新图形的各边长之比和周长之比等于这个比,而它们的面积之比等于这个比的平方。
将一个图形放大或缩小后,图形的大小变了,但形状不变。
把一个图形的各边按一定的比进行放大或缩小,从而得到该图形的放大图形或缩小图形。
课堂练习
1.图中A→B→C→D是怎样变过来的?
教材第92页“做一做”
向右平移5格
A
B
C
D
先向右平移5格,再绕中心逆时针旋转90°
先向右平移5格,再绕中心逆时针旋转90°
(1)风车转动是( )现象,推拉窗户是( )现象。(填“平移”或“旋转”)
旋转
平移
沿直线移动一定的距离。
2.填一填。
绕中心点逆时针转动360°。
(2)把一个边长为10厘米的正方形按3∶1放大,放大后所得图形的面积是( )平方厘米。
900
可以先求出放大后的边长再求放大后的面积;也可以先求出放大前的面积再求放大后的面积。
方法一:(10×3)2=900(cm2)
方法二:10×10×32=900(cm2)
(3)一个底面直径是4厘米、高是3厘米的圆柱,放大后底面的周长是62.8厘米,这个圆柱是按( )放大了,放大后的圆柱的底面积是( )平方厘米。
5∶1
314
放大后的底面直径:62.8÷3.14=20(cm)
放大后与放大前的比:20∶4=5∶1
放大后的底面积:3.14×(20÷2)2=314(cm2)
( )条
对称轴
( )条
对称轴
2
( )条
对称轴
(4)数一数,下面每幅图有几条对称轴?
无数
( )条
对称轴
0
5
(1)下面物体的运动方式中,( )与其他三种运动方式不同。
A.螺旋桨的运动
B.抽屉的拉动
C.风扇叶片的转动
D.钟摆的摆动
B
旋转
平移
旋转
旋转
3.选一选。
(2)将一张正方形纸片沿虚线向上对折,再沿虚线向右对折,得到一个正方形,然后剪下一个角,如下图所示。将这张纸片展开后应该是( )。
B
A
B
C
D
(3)下列各图形面积计算公式的推导过程中,没有用到平移或旋转的是( )。
A.三角形
B.梯形
C.圆
D.平行四边形
C
旋转、平移
旋转、平移
剪拼
割补、平移
4.如图,直角三角形ABC中的空白部分是正方形,正方形的一个顶点D将这个直角三角形的斜边分成两部分,已知AD=4 cm,CD=6 cm,求阴影部分的面积。
F
E
D
C
B
A
4 cm
6 cm
将三角形ADF绕D点逆时针旋转90°。
阴影部分就转化成了一个两条直角边分别是4 cm和6 cm的直角三角形。
4×6÷2=12(cm2)
答:阴影部分的面积是12 cm2。
4 cm
5.操作题。
(1)将图中A图形先向( )平移( )格,再向( )平移( )格,就能和B图形拼成一个正方形。
O
·
A
B
右 4
下 2
右 4
下 2
5.操作题。
(2)在图中画出B图形绕点O逆时针旋转90°后的图形。
O
·
A
B
B
(3)按2∶1的比画出B图形放大后的图形。
6.你能画出下面轴对称图形的另一半吗?
·
·
·
·
·
·
·
·
·
·
·
·
先找出已知图形的几个关键点,在对称轴的另一侧找出它们的对称点,按已知图形形状连接各对称点,就画出了轴对称图形的另一半。
人教版数学六年级(下)
整理和复习
第4课时 图形的运动
6
2.图形与几何
问题导入
我们学过哪些关于图形的运动的知识?
教材第92页
平移
旋转
放大
缩小
轴对称
平移、旋转和轴对称不改变图形的形状和大小。
图形的放大和缩小只改变图形的大小不改变形状。
哪些运动不改变图形的形状和大小?
哪些运动只改变图形的大小,而不改变形状?
归纳整理
什么是轴对称图形?什么叫对称轴?
轴对称图形:如果一个图形沿着一条直线对折,直线两侧的图形能够完全重合,这个图形就叫做轴对称图形。
对称轴:折痕所在的直线叫做对称轴。
什么是轴对称?
轴对称:把一个图形沿着某一条直线翻折,如果它能够与另一个图形完全重合,那么就说这两个图形关于这条直线对称。
A
B
C
D
E
F
l
对称点
对称轴
对称点:两个图形中的对应点叫做关于这条直线的对称点。
小组交流:回忆平移的相关知识,完成下表。
图形的平移
意义
要素
特点
画法
在同一平面内,将一个图形沿一直线移动一定的距离,这样的图形运动叫做平移。
平移的方向、平移的距离。
只改变图形的位置,不改变图形的形状、大小及方向。
先找出图形的关键点,再按要求平移相应的距离,最后把这些点顺次连接起来。
小组交流:回忆旋转的相关知识,完成下表。
图形的旋转
意义
要素
特点
画法
在平面内,将一个图形绕一个点按某个方向转动一个角度,这样的图形运动叫做旋转。
旋转中心、旋转方向、旋转角度。
图形的位置、方向都改变了,但形状和大小都不变。
先找准旋转中心,然后确定旋转的方向和旋转的角度,再分别旋转各边,最后画出各边的对应边。
将一个图形按一定的比放大或缩小,原图形与新图形的各边长之比和周长之比等于这个比,而它们的面积之比等于这个比的平方。
将一个图形放大或缩小后,图形的大小变了,但形状不变。
把一个图形的各边按一定的比进行放大或缩小,从而得到该图形的放大图形或缩小图形。
课堂练习
1.图中A→B→C→D是怎样变过来的?
教材第92页“做一做”
向右平移5格
A
B
C
D
先向右平移5格,再绕中心逆时针旋转90°
先向右平移5格,再绕中心逆时针旋转90°
(1)风车转动是( )现象,推拉窗户是( )现象。(填“平移”或“旋转”)
旋转
平移
沿直线移动一定的距离。
2.填一填。
绕中心点逆时针转动360°。
(2)把一个边长为10厘米的正方形按3∶1放大,放大后所得图形的面积是( )平方厘米。
900
可以先求出放大后的边长再求放大后的面积;也可以先求出放大前的面积再求放大后的面积。
方法一:(10×3)2=900(cm2)
方法二:10×10×32=900(cm2)
(3)一个底面直径是4厘米、高是3厘米的圆柱,放大后底面的周长是62.8厘米,这个圆柱是按( )放大了,放大后的圆柱的底面积是( )平方厘米。
5∶1
314
放大后的底面直径:62.8÷3.14=20(cm)
放大后与放大前的比:20∶4=5∶1
放大后的底面积:3.14×(20÷2)2=314(cm2)
( )条
对称轴
( )条
对称轴
2
( )条
对称轴
(4)数一数,下面每幅图有几条对称轴?
无数
( )条
对称轴
0
5
(1)下面物体的运动方式中,( )与其他三种运动方式不同。
A.螺旋桨的运动
B.抽屉的拉动
C.风扇叶片的转动
D.钟摆的摆动
B
旋转
平移
旋转
旋转
3.选一选。
(2)将一张正方形纸片沿虚线向上对折,再沿虚线向右对折,得到一个正方形,然后剪下一个角,如下图所示。将这张纸片展开后应该是( )。
B
A
B
C
D
(3)下列各图形面积计算公式的推导过程中,没有用到平移或旋转的是( )。
A.三角形
B.梯形
C.圆
D.平行四边形
C
旋转、平移
旋转、平移
剪拼
割补、平移
4.如图,直角三角形ABC中的空白部分是正方形,正方形的一个顶点D将这个直角三角形的斜边分成两部分,已知AD=4 cm,CD=6 cm,求阴影部分的面积。
F
E
D
C
B
A
4 cm
6 cm
将三角形ADF绕D点逆时针旋转90°。
阴影部分就转化成了一个两条直角边分别是4 cm和6 cm的直角三角形。
4×6÷2=12(cm2)
答:阴影部分的面积是12 cm2。
4 cm
5.操作题。
(1)将图中A图形先向( )平移( )格,再向( )平移( )格,就能和B图形拼成一个正方形。
O
·
A
B
右 4
下 2
右 4
下 2
5.操作题。
(2)在图中画出B图形绕点O逆时针旋转90°后的图形。
O
·
A
B
B
(3)按2∶1的比画出B图形放大后的图形。
6.你能画出下面轴对称图形的另一半吗?
·
·
·
·
·
·
·
·
·
·
·
·
先找出已知图形的几个关键点,在对称轴的另一侧找出它们的对称点,按已知图形形状连接各对称点,就画出了轴对称图形的另一半。
