人教版六年级数学下册 6总复习 4数学思考 第1课时 数学思考(1)(课件共17张PPT)
文档属性
| 名称 | 人教版六年级数学下册 6总复习 4数学思考 第1课时 数学思考(1)(课件共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-31 21:08:54 | ||
图片预览





文档简介
(共17张PPT)
人教版数学六年级(下)
整理和复习
第1课时 数学思考(1)
6
4.数学思考
复习导入
教材第100页
你能举例说一说你知道哪些数学思想和方法吗?
数形结合思想
转化思想
假设法
符号化思想
方程思想
分类思想
类比思想
对应思想
……
数学思想和方法可以帮助我们有条理地思考,简捷地解决问题。
1. 6个点可以连多少条线段?8个点呢?
合作探究
教材第100页第1题
别着急,从2个点开始,逐渐增加点数,找找规律。
太乱了,我都数昏了。
点数
增加条数
总条数
2个点
3个点
4个点
5个点
6个点
2
3
4
5
3
6
10
15
1
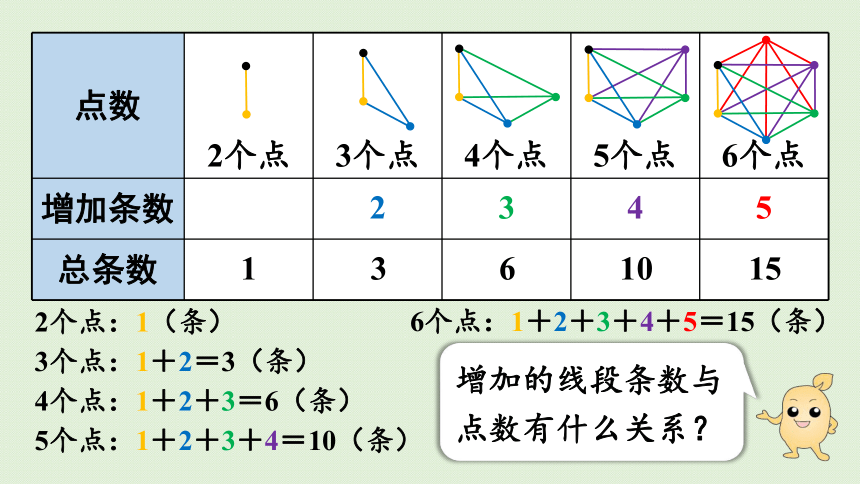
2个点:1(条)
3个点:1+2=3(条)
4个点:1+2+3=6(条)
5个点:1+2+3+4=10(条)
6个点:1+2+3+4+5=15(条)
增加的线段条数与点数有什么关系?
点数
增加条数
总条数
2个点
3个点
4个点
5个点
6个点
2
3
4
5
3
6
10
15
1
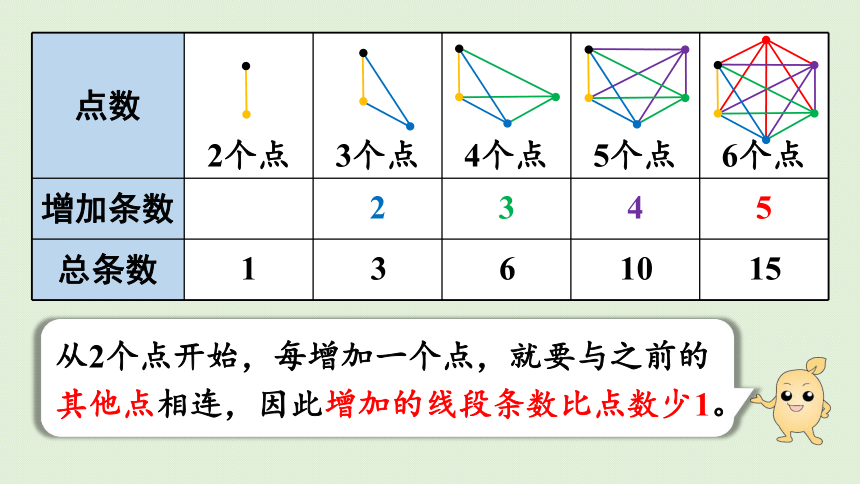
从2个点开始,每增加一个点,就要与之前的其他点相连,因此增加的线段条数比点数少1。
7个点:1+2+3+4+5+6=21(条)
8个点:1+2+3+4+5+6+7=28(条)
12个点可以连多少条线段?20个点呢?
12个点:1+2+3+4+5+6+7+8+9+10
+11=66(条)
20个点:1+2+3+4+5+6+7+8+9+10+11+12
+13+14+15+16+17+18+19=190(条)
归纳整理
n个点:1+2+3+…+(n-1)
计算有几条线段,就是从1+2+3+…一直加到比点数少1的数再求和。
n个点可以连多少条线段呢?
=n(n-1)÷2(条)(n≥2)
等差数列的和=(首项+尾项)×项数÷2
=[1+(n-1)]×(n-1)÷2
课堂练习
1.观察下图,想一想。
教材第100页“做一做”
(1)第7幅图有多少个棋子?
(1) (2) (3) (4)
……
先数一数每幅图各有多少个棋子。
1个
4个
9个
16个
1×1
2×2
3×3
4×4
1.观察下图,想一想。
(1)第7幅图有多少个棋子?
(1) (2) (3) (4)
……
7×7=49(个),第7幅图有49个棋子。
1个
4个
9个
16个
1×1
2×2
3×3
4×4
1.观察下图,想一想。
(1)第15幅图呢?
(1) (2) (3) (4)
……
15×15=225(个),第15幅图有225个棋子。
1个
4个
9个
16个
1×1
2×2
3×3
4×4
1.观察下图,想一想。
(2)*第n幅图有多少个棋子?
(1) (2) (3) (4)
……
每幅图的行数和列数都等于它的序号,n×n=n2(个),因此第n幅图有n2个棋子。
1个
4个
9个
16个
1×1
2×2
3×3
4×4
2.按规律填数。
(1)8、11、14、17、( )、23、……
+3
+3
+3
+3
20
+3
(2)一列数1、2、2、3、3、3、4、4、4、4、……中的第35个数是( )
1个1
2个2
3个3
4个4
+ + + + 5 + 6 + 7 + 8 =36
8
第36个数是第8个8,第35个数是第7个8。
3.摆一摆,找规律。
(1)
(1)摆第7个图形需要( )根小棒。
1+2
15
(2)
(3)
(4)
…
1+2+2
1+2+2+2
1+2+2+2+2
1+2×1
1+2×2
1+2×3
1+2×4
(2)摆第n个图形需要( )根小棒。
1+2×7=15
小棒数比图形数的2倍多1。
1+2×n=1+2n
1+2n
4.用小棒按照如图所示的方式摆图形,摆1个六边形需要6根小棒,摆4个六边形需要( )根小棒,摆n个六边形需要( )根小棒。
(1)
21
(2)
(3)
(4)
1+5n
1+5
1+5+5
1+5+5+5
1+5+5+5+5
小棒数比图形数的5倍多1。
6根
11根
16根
21根
拓展提升
1.下面的图案是由若干个相同的正方形组成的,每个阴影部分的面积是4平方米,占每个正方形面积的-。由20个正方形像这样组成的面积是( )平方米。
19
…
644
4÷-=36(平方米)
19
36-4=32(平方米)
36
+32
+32
+32
+32
+32
+…
4+32
4+32×20=644(平方米)
2.如图所示的三个图形都是用同样大小的三角形按一定规律拼成的一组图形。
…
(1)第5个图形中,有( )个白三角形。
21
第1个
第2个
第3个
1+2=3
1+2+3=6
1+2+3+4=10
1+2+3+4+5+6=21
…
(2)第( )个图形中,白三角形比黄三角形多2021个。
2020
第1个
第2个
第3个
多2个
多3个
多4个
2021-1=2020(个)
2.如图所示的三个图形都是用同样大小的三角形按一定规律拼成的一组图形。
人教版数学六年级(下)
整理和复习
第1课时 数学思考(1)
6
4.数学思考
复习导入
教材第100页
你能举例说一说你知道哪些数学思想和方法吗?
数形结合思想
转化思想
假设法
符号化思想
方程思想
分类思想
类比思想
对应思想
……
数学思想和方法可以帮助我们有条理地思考,简捷地解决问题。
1. 6个点可以连多少条线段?8个点呢?
合作探究
教材第100页第1题
别着急,从2个点开始,逐渐增加点数,找找规律。
太乱了,我都数昏了。
点数
增加条数
总条数
2个点
3个点
4个点
5个点
6个点
2
3
4
5
3
6
10
15
1
2个点:1(条)
3个点:1+2=3(条)
4个点:1+2+3=6(条)
5个点:1+2+3+4=10(条)
6个点:1+2+3+4+5=15(条)
增加的线段条数与点数有什么关系?
点数
增加条数
总条数
2个点
3个点
4个点
5个点
6个点
2
3
4
5
3
6
10
15
1
从2个点开始,每增加一个点,就要与之前的其他点相连,因此增加的线段条数比点数少1。
7个点:1+2+3+4+5+6=21(条)
8个点:1+2+3+4+5+6+7=28(条)
12个点可以连多少条线段?20个点呢?
12个点:1+2+3+4+5+6+7+8+9+10
+11=66(条)
20个点:1+2+3+4+5+6+7+8+9+10+11+12
+13+14+15+16+17+18+19=190(条)
归纳整理
n个点:1+2+3+…+(n-1)
计算有几条线段,就是从1+2+3+…一直加到比点数少1的数再求和。
n个点可以连多少条线段呢?
=n(n-1)÷2(条)(n≥2)
等差数列的和=(首项+尾项)×项数÷2
=[1+(n-1)]×(n-1)÷2
课堂练习
1.观察下图,想一想。
教材第100页“做一做”
(1)第7幅图有多少个棋子?
(1) (2) (3) (4)
……
先数一数每幅图各有多少个棋子。
1个
4个
9个
16个
1×1
2×2
3×3
4×4
1.观察下图,想一想。
(1)第7幅图有多少个棋子?
(1) (2) (3) (4)
……
7×7=49(个),第7幅图有49个棋子。
1个
4个
9个
16个
1×1
2×2
3×3
4×4
1.观察下图,想一想。
(1)第15幅图呢?
(1) (2) (3) (4)
……
15×15=225(个),第15幅图有225个棋子。
1个
4个
9个
16个
1×1
2×2
3×3
4×4
1.观察下图,想一想。
(2)*第n幅图有多少个棋子?
(1) (2) (3) (4)
……
每幅图的行数和列数都等于它的序号,n×n=n2(个),因此第n幅图有n2个棋子。
1个
4个
9个
16个
1×1
2×2
3×3
4×4
2.按规律填数。
(1)8、11、14、17、( )、23、……
+3
+3
+3
+3
20
+3
(2)一列数1、2、2、3、3、3、4、4、4、4、……中的第35个数是( )
1个1
2个2
3个3
4个4
+ + + + 5 + 6 + 7 + 8 =36
8
第36个数是第8个8,第35个数是第7个8。
3.摆一摆,找规律。
(1)
(1)摆第7个图形需要( )根小棒。
1+2
15
(2)
(3)
(4)
…
1+2+2
1+2+2+2
1+2+2+2+2
1+2×1
1+2×2
1+2×3
1+2×4
(2)摆第n个图形需要( )根小棒。
1+2×7=15
小棒数比图形数的2倍多1。
1+2×n=1+2n
1+2n
4.用小棒按照如图所示的方式摆图形,摆1个六边形需要6根小棒,摆4个六边形需要( )根小棒,摆n个六边形需要( )根小棒。
(1)
21
(2)
(3)
(4)
1+5n
1+5
1+5+5
1+5+5+5
1+5+5+5+5
小棒数比图形数的5倍多1。
6根
11根
16根
21根
拓展提升
1.下面的图案是由若干个相同的正方形组成的,每个阴影部分的面积是4平方米,占每个正方形面积的-。由20个正方形像这样组成的面积是( )平方米。
19
…
644
4÷-=36(平方米)
19
36-4=32(平方米)
36
+32
+32
+32
+32
+32
+…
4+32
4+32×20=644(平方米)
2.如图所示的三个图形都是用同样大小的三角形按一定规律拼成的一组图形。
…
(1)第5个图形中,有( )个白三角形。
21
第1个
第2个
第3个
1+2=3
1+2+3=6
1+2+3+4=10
1+2+3+4+5+6=21
…
(2)第( )个图形中,白三角形比黄三角形多2021个。
2020
第1个
第2个
第3个
多2个
多3个
多4个
2021-1=2020(个)
2.如图所示的三个图形都是用同样大小的三角形按一定规律拼成的一组图形。
