人教版六年级数学下册 6总复习 4数学思考 第3课时 数学思考(3)课件(共17张PPT)
文档属性
| 名称 | 人教版六年级数学下册 6总复习 4数学思考 第3课时 数学思考(3)课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-31 21:08:19 | ||
图片预览



文档简介
(共17张PPT)
人教版数学六年级(下)
整理和复习
第3课时 数学思考(3)
6
4.数学思考
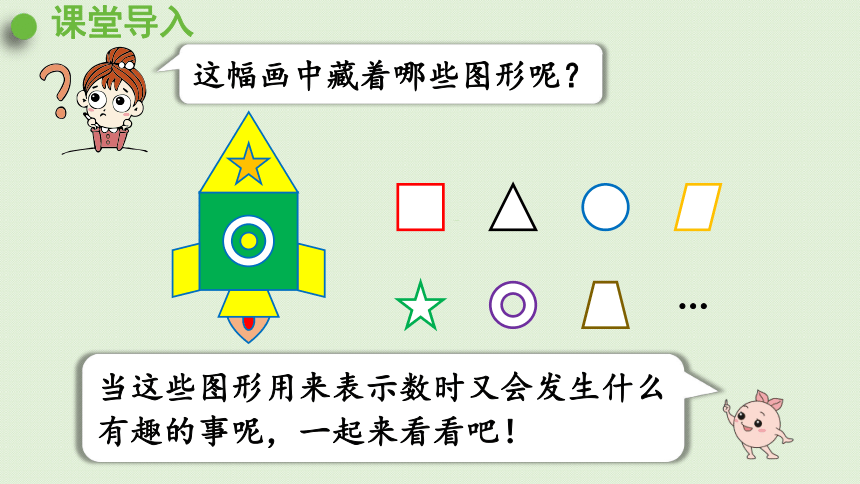
课堂导入
…
这幅画中藏着哪些图形呢?
当这些图形用来表示数时又会发生什么有趣的事呢,一起来看看吧!
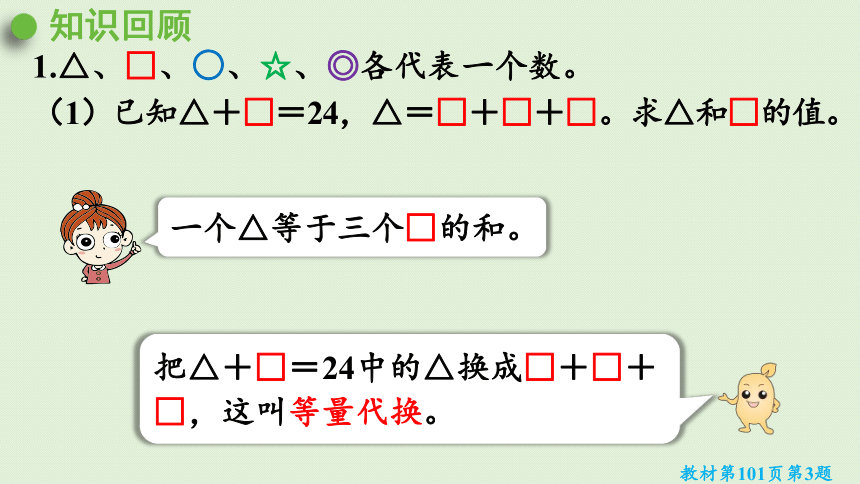
1.△、□、○、☆、◎各代表一个数。
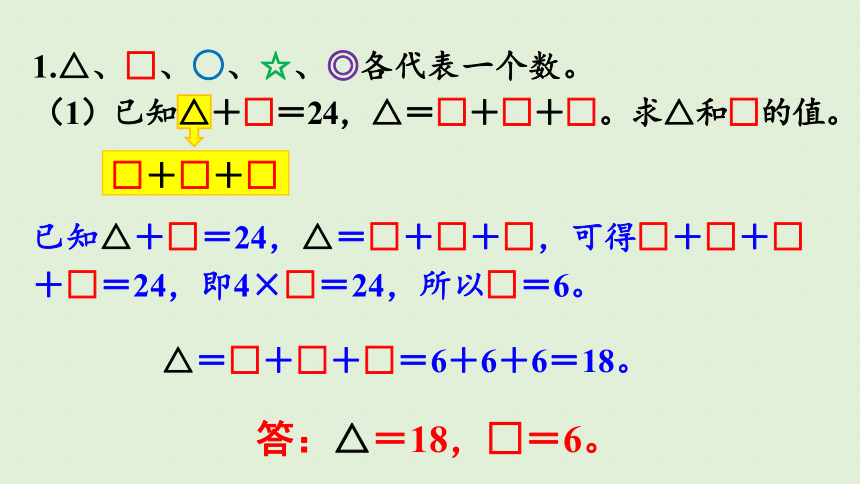
(1)已知△+□=24,△=□+□+□。求△和□的值。
一个△等于三个□的和。
教材第101页第3题
把△+□=24中的△换成□+□+□,这叫等量代换。
知识回顾
□+□+□
已知△+□=24,△=□+□+□,可得□+□+□ +□=24,即4×□=24,所以□=6。
△=□+□+□=6+6+6=18。
答:△=18,□=6。
(1)已知△+□=24,△=□+□+□。求△和□的值。
1.△、□、○、☆、◎各代表一个数。
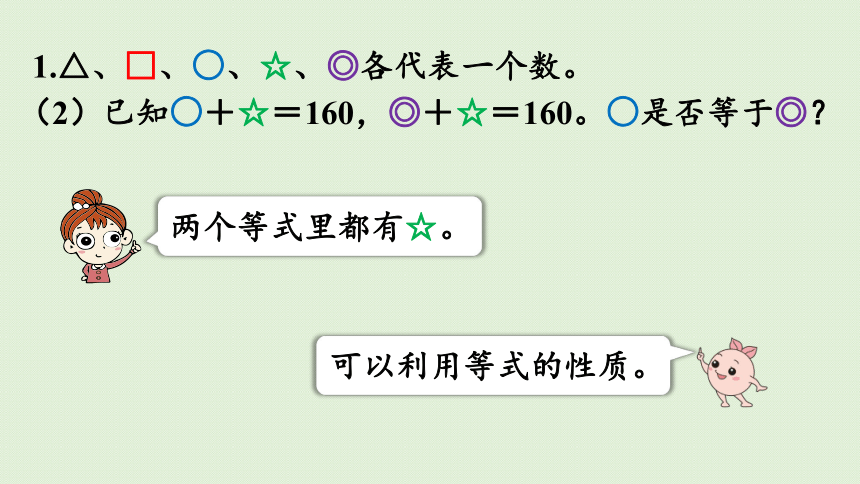
(2)已知○+☆=160,◎+☆=160。○是否等于◎?
两个等式里都有☆。
可以利用等式的性质。
1.△、□、○、☆、◎各代表一个数。
◎=160-☆
(2)已知○+☆=160,◎+☆=160。○是否等于◎?
○=160-☆
已知○+☆=160,◎+☆=160,根据等式的性质,等式两边都减去☆。
可以推出○=160-☆,◎=160-☆。
因为☆代表同一个数,所以○等于◎。
答:○等于◎。
1.△、□、○、☆、◎各代表一个数。
等量代换
等量代换是指用一个量来代替与它相等的另一个量,它是数学中一种基本的思想方法,也是代数思想方法的基础。
教材第102页第4题
2.什么是平角?平角与直线有什么区别?
一条射线绕它的端点旋转,当始边和终边在同一条直线上,方向相反时,所构成的角叫平角。
平角是“角”,有一个顶点和两条边,可度量;直线是“线”,不可度量。
1
2
3
4
根据平角的定义判断哪两个角可以组成平角。
如右图,两条直线相交于点O。
1
2
3
4
·
O
(1)每相邻两个角可以组成一个平角,一共能组成几个平角?
·
O
1
2
3
4
·
O
1
2
3
4
·
O
1
2
3
4
·
O
答:平角的两边在一条直线上,一共能组成4个平角:∠1和∠2组成的平角,∠2和∠3组成的平角,∠3和∠4组成的平角,∠4和∠1组成的平角。
把∠1和∠2,∠2和∠3用等量关系表示出来。
如右图,两条直线相交于点O。
1
2
3
4
·
O
(2)你能推出∠1=∠3吗?
1
2
·
O
2
3
·
O
∠1和∠2,∠2和∠3都能组成平角。
如右图,两条直线相交于点O。
1
2
3
4
·
O
(2)你能推出∠1=∠3吗?
已知∠1+∠2=180°,∠2+∠3=180°,根据等式的性质,等式两边都减去∠2。
可以推出∠1=180°-∠2,∠3=180°-∠2。
因为180°-∠2=180°-∠2,所以∠1=∠3。
△+△+△
课堂练习
1.☆、△、○、□各代表一个数,根据下面的已知条件,求☆、△、○、□的值。
(1)已知☆-△=12,☆=△+△+△。
已知☆-△=12,☆=△+△+△,可得△+△+△-△=12,即2×△=12,所以△=6。
☆=△+△+△=6+6+6=18
答:☆=18,△=6。
○+○+○+○+○+□+□+□+□+□
1.☆、△、○、□各代表一个数,根据下面的已知条件,求☆、△、○、□的值。
(2)已知○+○+□+□+□=54,
○+○+○+□+□=46。
已知○+○+□+□+□=54,○+○+○+□+□=46,可得5×○+5×□=100,则○+□=100÷5=20。
○+○+□+○+□
(2)已知○+○+□+□+□=54,
○+○+○+□+□=46。
因为○+20+20=46,所以○=46-20-20=6;
因为○+□=20,所以□=20-6=14。
答:○=6,□=14。
20
20
1.☆、△、○、□各代表一个数,根据下面的已知条件,求☆、△、○、□的值。
2.如图,把三角形ABC的边AB延长到点D,BC延长到点E。
A
B
C
D
E
1
2
3
4
5
(1)图中的哪些角拼成的是平角?
答:图中的∠2和∠5组成的是平角,∠3和∠4组成的也是平角。
平角的两边在一条直线上。
2.如图,把三角形ABC的边AB延长到点D,BC延长到点E。
A
B
C
D
E
1
2
3
4
5
(2)你能说明∠5=∠1+∠3吗?
因为∠2+∠5=180°,
∠1+∠2+∠3=180°,
可得∠2+∠5=∠1+∠2+∠3,
根据等式的性质,等式两边都减去∠2,
所以∠5=∠1+∠3。
2.如图,把三角形ABC的边AB延长到点D,BC延长到点E。
A
B
C
D
E
1
2
3
4
5
(3)若∠1=60°,∠4=110°,那么∠2是多少度?
因为∠3+∠4=180°,
∠1+∠2+∠3=180°,
可得∠4=∠1+∠2;
已知∠1=60°,∠4=110°,
所以∠2=110°-60°=50°。
人教版数学六年级(下)
整理和复习
第3课时 数学思考(3)
6
4.数学思考
课堂导入
…
这幅画中藏着哪些图形呢?
当这些图形用来表示数时又会发生什么有趣的事呢,一起来看看吧!
1.△、□、○、☆、◎各代表一个数。
(1)已知△+□=24,△=□+□+□。求△和□的值。
一个△等于三个□的和。
教材第101页第3题
把△+□=24中的△换成□+□+□,这叫等量代换。
知识回顾
□+□+□
已知△+□=24,△=□+□+□,可得□+□+□ +□=24,即4×□=24,所以□=6。
△=□+□+□=6+6+6=18。
答:△=18,□=6。
(1)已知△+□=24,△=□+□+□。求△和□的值。
1.△、□、○、☆、◎各代表一个数。
(2)已知○+☆=160,◎+☆=160。○是否等于◎?
两个等式里都有☆。
可以利用等式的性质。
1.△、□、○、☆、◎各代表一个数。
◎=160-☆
(2)已知○+☆=160,◎+☆=160。○是否等于◎?
○=160-☆
已知○+☆=160,◎+☆=160,根据等式的性质,等式两边都减去☆。
可以推出○=160-☆,◎=160-☆。
因为☆代表同一个数,所以○等于◎。
答:○等于◎。
1.△、□、○、☆、◎各代表一个数。
等量代换
等量代换是指用一个量来代替与它相等的另一个量,它是数学中一种基本的思想方法,也是代数思想方法的基础。
教材第102页第4题
2.什么是平角?平角与直线有什么区别?
一条射线绕它的端点旋转,当始边和终边在同一条直线上,方向相反时,所构成的角叫平角。
平角是“角”,有一个顶点和两条边,可度量;直线是“线”,不可度量。
1
2
3
4
根据平角的定义判断哪两个角可以组成平角。
如右图,两条直线相交于点O。
1
2
3
4
·
O
(1)每相邻两个角可以组成一个平角,一共能组成几个平角?
·
O
1
2
3
4
·
O
1
2
3
4
·
O
1
2
3
4
·
O
答:平角的两边在一条直线上,一共能组成4个平角:∠1和∠2组成的平角,∠2和∠3组成的平角,∠3和∠4组成的平角,∠4和∠1组成的平角。
把∠1和∠2,∠2和∠3用等量关系表示出来。
如右图,两条直线相交于点O。
1
2
3
4
·
O
(2)你能推出∠1=∠3吗?
1
2
·
O
2
3
·
O
∠1和∠2,∠2和∠3都能组成平角。
如右图,两条直线相交于点O。
1
2
3
4
·
O
(2)你能推出∠1=∠3吗?
已知∠1+∠2=180°,∠2+∠3=180°,根据等式的性质,等式两边都减去∠2。
可以推出∠1=180°-∠2,∠3=180°-∠2。
因为180°-∠2=180°-∠2,所以∠1=∠3。
△+△+△
课堂练习
1.☆、△、○、□各代表一个数,根据下面的已知条件,求☆、△、○、□的值。
(1)已知☆-△=12,☆=△+△+△。
已知☆-△=12,☆=△+△+△,可得△+△+△-△=12,即2×△=12,所以△=6。
☆=△+△+△=6+6+6=18
答:☆=18,△=6。
○+○+○+○+○+□+□+□+□+□
1.☆、△、○、□各代表一个数,根据下面的已知条件,求☆、△、○、□的值。
(2)已知○+○+□+□+□=54,
○+○+○+□+□=46。
已知○+○+□+□+□=54,○+○+○+□+□=46,可得5×○+5×□=100,则○+□=100÷5=20。
○+○+□+○+□
(2)已知○+○+□+□+□=54,
○+○+○+□+□=46。
因为○+20+20=46,所以○=46-20-20=6;
因为○+□=20,所以□=20-6=14。
答:○=6,□=14。
20
20
1.☆、△、○、□各代表一个数,根据下面的已知条件,求☆、△、○、□的值。
2.如图,把三角形ABC的边AB延长到点D,BC延长到点E。
A
B
C
D
E
1
2
3
4
5
(1)图中的哪些角拼成的是平角?
答:图中的∠2和∠5组成的是平角,∠3和∠4组成的也是平角。
平角的两边在一条直线上。
2.如图,把三角形ABC的边AB延长到点D,BC延长到点E。
A
B
C
D
E
1
2
3
4
5
(2)你能说明∠5=∠1+∠3吗?
因为∠2+∠5=180°,
∠1+∠2+∠3=180°,
可得∠2+∠5=∠1+∠2+∠3,
根据等式的性质,等式两边都减去∠2,
所以∠5=∠1+∠3。
2.如图,把三角形ABC的边AB延长到点D,BC延长到点E。
A
B
C
D
E
1
2
3
4
5
(3)若∠1=60°,∠4=110°,那么∠2是多少度?
因为∠3+∠4=180°,
∠1+∠2+∠3=180°,
可得∠4=∠1+∠2;
已知∠1=60°,∠4=110°,
所以∠2=110°-60°=50°。
