24.1.1圆-同步练习 2021-2022学年九年级数学上册人教版(word版含答案)
文档属性
| 名称 | 24.1.1圆-同步练习 2021-2022学年九年级数学上册人教版(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 578.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-01 00:00:00 | ||
图片预览




文档简介
2021-2022学年九年级数学上册(人教版)教材同步
24.1.1圆-同步练习
时间:60分钟
一、单选题
1.过圆上一点可以做圆的最长弦( )
A.1条 B.2条 C.3条 D.4条
2.如图,在⊙O中,点B,O,C和点A,O,D分别在同一条直线上,则图中有( )条弦.
A.2 B.3 C.4 D.5
3.一块圆形木板,它的半径是,它的面积是( )
A. B. C. D.
4.若所在平面内一点P到上的点的最大距离为8,最小距离是2,则此圆的半径是( )
A.5 B.3 C.5或3 D.10或6
5.一个在圆内的点,它到圆上的最近距离为3cm,到最远距离为5cm,那么圆的半径为( )
A.5cm B.3cm C.8cm D.4cm
6.如图所示,在⊙O中,点A,O,D以及点B,O,C分别在一条直线上,则图中的弦有( )
A.2条 B.3条 C.4条 D.5条
7.下列说法:①一个圆上的各点都在这个圆的圆周上;②以圆心为端点的线段是半径;③同一圆上的点到圆心的距离相等;④半径确定了,圆就确定了其中正确的是( )
A.①② B.①③④ C.①③ D.②④
8.如图,长方形中,,点E是折线段上的一个动点(与点A不重合),点P是点A关于的对称点.在点E的运动过程中,能使得为等腰三角形的点E的位置共有( )
A.2个 B.3个 C.4个 D.5个
二、填空题
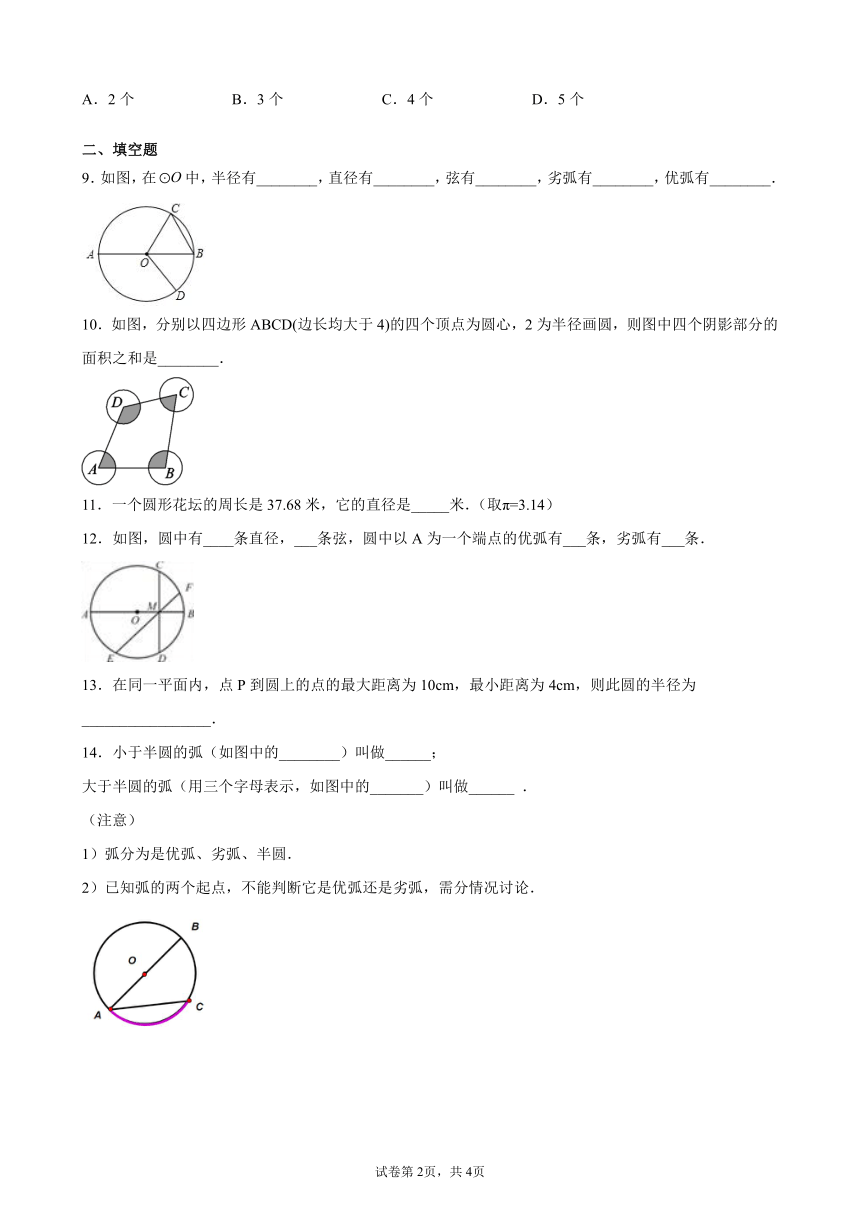
9.如图,在中,半径有________,直径有________,弦有________,劣弧有________,优弧有________.
10.如图,分别以四边形ABCD(边长均大于4)的四个顶点为圆心,2为半径画圆,则图中四个阴影部分的面积之和是________.
11.一个圆形花坛的周长是37.68米,它的直径是_____米.(取π=3.14)
12.如图,圆中有____条直径,___条弦,圆中以A为一个端点的优弧有___条,劣弧有___条.
13.在同一平面内,点P到圆上的点的最大距离为10cm,最小距离为4cm,则此圆的半径为_________________.
14.小于半圆的弧(如图中的________)叫做______;
大于半圆的弧(用三个字母表示,如图中的_______)叫做______ .
(注意)
1)弧分为是优弧、劣弧、半圆.
2)已知弧的两个起点,不能判断它是优弧还是劣弧,需分情况讨论.
三、解答题
15.找出图中所有的弦、优弧和劣弧.
16.一个圆的半径从3厘米扩大到7厘米,它的面积增加了多少平方厘米?
17.如下图,在半径为5米的圆形花坛周 围修一条宽1米的小路,求小路的面积.
18.已知:线段AB = 4 cm,画图说明:和点A、B的距离都不大于3 cm的所有点组成的图形.
19.已知,以长为半径作圆,使它经过点A和点B.这样的圆能作出几个?
20.如图所示,在⊙O上有一点C(C不与A、B重合),在直径AB上有一个动点P(P不与A、B重合).试判断PA、PC、PB的大小关系,并说明理由.
21.(1)从A地到B地,某甲走直径AB上方的半圆途径;乙先走直径AC上方半圆的途径,再走直径CB下方半圆的途径,如图1,已知AB=40米,AC=30米,计算个人所走的路程,并比较两人所走路程的远近;
(2)如果甲.乙走的路程图改成图2,两人走的路程远近相同吗?
22.如图,某田径场的周长(内圈)为,其中两个弯道内圈(半圆形)共长,直线段共长,而每条跑道宽约(共6条跑道).
(1)内圈弯道半径为多少米?(结果精确到)
(2)一个内圈弯道与一个外圈弯道的长相差多少米?(结果精确到)
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.A
【解析】圆的最长的弦是直径,直径经过圆心,过圆上一点和圆心可以确定一条直线,所以过圆上一点可以作出圆的最长弦的条数为一条.
故选:A.
2.B
【解析】根据弦的概念,AB、BC、EC为圆的弦,共有3条弦.
故选B.
3.C
【解析】解:∵一块圆形木板,它的半径是,
∴;
故选:C.
4.C
【解析】解:设的半径为,
当点在圆外时,;
当点在内时,.
综上可知此圆的半径为3或5.
故选:C.
5.D
【解析】圆内的点到圆上的最近距离和最远距离之和为此圆的直径,故半径为cm.
故选D.
6.B
【解析】图中的弦有AB,BC,CE共三条,
故选B.
7.C
【解析】圆周上的各点是组成圆的要素,故①正确;
以圆心为端点,另一个端点在圆上的线段是圆的半径,故②错误;
同一圆上的点到圆心的距离相等,且都等于半径,故③正确;
圆心和半径共同确定一个圆,半径确定了,圆心位置不确定,圆也不能确定,故④错误.
故选:C.
8.C
【解析】根据题意P点在以B为圆心BA为半径的圆上,并且只在右边的半圆上,
分为三种情况:①如图1,以BC为底时,有两个,
是BC的垂直平分线与以B为圆心BA为半径的圆的交点和,
此时;
②如图2,以BP为底,C为顶点时,有两个,
是以B为圆心BA为半径的圆与以C为圆心BC为半径的圆的交点和,
此时;
③以CP为底,B为顶点时,没有,
是以B为圆心BA为半径的圆与以B为圆心BC为半径的圆的交点,但不存在;
综上满足要求的P有4个,
故选:C.
9.,,, , ,,,, ,,,,
【解析】解:在中,半径有,,,;直径有;弦有,;劣弧有,,,,;优弧有,,,,;
故答案为:,,,;;,;,,,,;,,,,.
10.4π
【解析】解:∵平行四边形ABCD的边长均大于4,各弧的半径都是2,
∴图中阴影部分的面积等于一个圆的面积,
即π 22=4π.
故答案为4π.
11.12
【解析】解:d = = .
故答案为:12.
12.1 3 4 4
【解析】圆中有AB一条直径,AB、CD、EF三条弦,圆中以A为一个端点的优弧有四条,劣弧有四条,
故答案为1,3,4,4.
13.3cm或7cm
【解析】设⊙O的半径为r,
当点P在圆外时,r==3cm;
当点P在⊙O内时,r=cm.
故答案为:3cm或7cm.
14. 劣弧 优弧
【解析】略
15.弦有:弦,弦,弦;优弧:,,,;劣弧:,,,
【解析】解:弦有:弦,弦,弦;优弧:,,,;劣弧:,,,.
16.平方厘米
【解析】解:根据题意,则
(平方厘米);
∴它的面积增加了125.6平方厘米.
17.28.26平方米
【解析】外圆半径r1为5米,围修一条宽1米的小路
∴内圆半径r2为4米
圆环的面积为
=πr12-πr22=3.14×5×5-3.14×4×4=78.5-50.24=28.26
∴小路的面积为28.26平方米.
18.所求图形为阴影部分(包括阴影的边界).
【解析】如图所示,以点A,B为圆心,3cm为半径画圆,两个圆相交的部分为阴影部分,图中阴影部分就是到点A和点B的距离都不大于3 cm的所有点组成的图形.
19.2个
【解析】解:这样的圆能画2个.如图:
作的垂直平分线,再以点为圆心,为半径作圆交于和,然后分别以和为圆心,以为半径作圆,
则和为所求圆.
20.当点P在OA上时PA<PC<PB,OB上时PB<PC<PA,当点P在点O处时PA=PB=PC.
【解析】当点P与点O重合时,PA=PB=PC,
当点P在OA上时,PA<PC<PB.
理由:连接OC,
在△POC中,OC-OP<PC<OP+OC,
∵OA=OB=OC,
∴OA-OP<PC<OP+OB,∴PA<PC<PB,
同理,当P点在OB上时,PB<PC<PA.
21.(1)相等;(2)相等.
【解析】(1)BC=AB-AC=10,
甲所走的路径长= 2 π = 2 π =20π(m),
乙所走的路径长= 2 π + 2 π = 2 π + π =20π(m),
所以两人所走路程的相等;
(2)两人走的路程远近相同.理由如下:甲所走的路径长= 2 π =π AB,
乙所走的路径长= 2 π + 2 π + π =π(AC+CD+DB)=π AB,
即两人走的路程远近相同.
22.(1)约;(2)约
【解析】解:(1)根据题意得:内圈弯道半径为 (米),
答:内圈弯道半径约为;
(2)由(1)得:外圈弯道半径为 (米),
一个内圈弯道与一个外圈弯道的长相差为 (米),
答:一个内圈弯道与一个外圈弯道的长相差约.答案第1页,共2页
答案第1页,共2页
24.1.1圆-同步练习
时间:60分钟
一、单选题
1.过圆上一点可以做圆的最长弦( )
A.1条 B.2条 C.3条 D.4条
2.如图,在⊙O中,点B,O,C和点A,O,D分别在同一条直线上,则图中有( )条弦.
A.2 B.3 C.4 D.5
3.一块圆形木板,它的半径是,它的面积是( )
A. B. C. D.
4.若所在平面内一点P到上的点的最大距离为8,最小距离是2,则此圆的半径是( )
A.5 B.3 C.5或3 D.10或6
5.一个在圆内的点,它到圆上的最近距离为3cm,到最远距离为5cm,那么圆的半径为( )
A.5cm B.3cm C.8cm D.4cm
6.如图所示,在⊙O中,点A,O,D以及点B,O,C分别在一条直线上,则图中的弦有( )
A.2条 B.3条 C.4条 D.5条
7.下列说法:①一个圆上的各点都在这个圆的圆周上;②以圆心为端点的线段是半径;③同一圆上的点到圆心的距离相等;④半径确定了,圆就确定了其中正确的是( )
A.①② B.①③④ C.①③ D.②④
8.如图,长方形中,,点E是折线段上的一个动点(与点A不重合),点P是点A关于的对称点.在点E的运动过程中,能使得为等腰三角形的点E的位置共有( )
A.2个 B.3个 C.4个 D.5个
二、填空题
9.如图,在中,半径有________,直径有________,弦有________,劣弧有________,优弧有________.
10.如图,分别以四边形ABCD(边长均大于4)的四个顶点为圆心,2为半径画圆,则图中四个阴影部分的面积之和是________.
11.一个圆形花坛的周长是37.68米,它的直径是_____米.(取π=3.14)
12.如图,圆中有____条直径,___条弦,圆中以A为一个端点的优弧有___条,劣弧有___条.
13.在同一平面内,点P到圆上的点的最大距离为10cm,最小距离为4cm,则此圆的半径为_________________.
14.小于半圆的弧(如图中的________)叫做______;
大于半圆的弧(用三个字母表示,如图中的_______)叫做______ .
(注意)
1)弧分为是优弧、劣弧、半圆.
2)已知弧的两个起点,不能判断它是优弧还是劣弧,需分情况讨论.
三、解答题
15.找出图中所有的弦、优弧和劣弧.
16.一个圆的半径从3厘米扩大到7厘米,它的面积增加了多少平方厘米?
17.如下图,在半径为5米的圆形花坛周 围修一条宽1米的小路,求小路的面积.
18.已知:线段AB = 4 cm,画图说明:和点A、B的距离都不大于3 cm的所有点组成的图形.
19.已知,以长为半径作圆,使它经过点A和点B.这样的圆能作出几个?
20.如图所示,在⊙O上有一点C(C不与A、B重合),在直径AB上有一个动点P(P不与A、B重合).试判断PA、PC、PB的大小关系,并说明理由.
21.(1)从A地到B地,某甲走直径AB上方的半圆途径;乙先走直径AC上方半圆的途径,再走直径CB下方半圆的途径,如图1,已知AB=40米,AC=30米,计算个人所走的路程,并比较两人所走路程的远近;
(2)如果甲.乙走的路程图改成图2,两人走的路程远近相同吗?
22.如图,某田径场的周长(内圈)为,其中两个弯道内圈(半圆形)共长,直线段共长,而每条跑道宽约(共6条跑道).
(1)内圈弯道半径为多少米?(结果精确到)
(2)一个内圈弯道与一个外圈弯道的长相差多少米?(结果精确到)
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.A
【解析】圆的最长的弦是直径,直径经过圆心,过圆上一点和圆心可以确定一条直线,所以过圆上一点可以作出圆的最长弦的条数为一条.
故选:A.
2.B
【解析】根据弦的概念,AB、BC、EC为圆的弦,共有3条弦.
故选B.
3.C
【解析】解:∵一块圆形木板,它的半径是,
∴;
故选:C.
4.C
【解析】解:设的半径为,
当点在圆外时,;
当点在内时,.
综上可知此圆的半径为3或5.
故选:C.
5.D
【解析】圆内的点到圆上的最近距离和最远距离之和为此圆的直径,故半径为cm.
故选D.
6.B
【解析】图中的弦有AB,BC,CE共三条,
故选B.
7.C
【解析】圆周上的各点是组成圆的要素,故①正确;
以圆心为端点,另一个端点在圆上的线段是圆的半径,故②错误;
同一圆上的点到圆心的距离相等,且都等于半径,故③正确;
圆心和半径共同确定一个圆,半径确定了,圆心位置不确定,圆也不能确定,故④错误.
故选:C.
8.C
【解析】根据题意P点在以B为圆心BA为半径的圆上,并且只在右边的半圆上,
分为三种情况:①如图1,以BC为底时,有两个,
是BC的垂直平分线与以B为圆心BA为半径的圆的交点和,
此时;
②如图2,以BP为底,C为顶点时,有两个,
是以B为圆心BA为半径的圆与以C为圆心BC为半径的圆的交点和,
此时;
③以CP为底,B为顶点时,没有,
是以B为圆心BA为半径的圆与以B为圆心BC为半径的圆的交点,但不存在;
综上满足要求的P有4个,
故选:C.
9.,,, , ,,,, ,,,,
【解析】解:在中,半径有,,,;直径有;弦有,;劣弧有,,,,;优弧有,,,,;
故答案为:,,,;;,;,,,,;,,,,.
10.4π
【解析】解:∵平行四边形ABCD的边长均大于4,各弧的半径都是2,
∴图中阴影部分的面积等于一个圆的面积,
即π 22=4π.
故答案为4π.
11.12
【解析】解:d = = .
故答案为:12.
12.1 3 4 4
【解析】圆中有AB一条直径,AB、CD、EF三条弦,圆中以A为一个端点的优弧有四条,劣弧有四条,
故答案为1,3,4,4.
13.3cm或7cm
【解析】设⊙O的半径为r,
当点P在圆外时,r==3cm;
当点P在⊙O内时,r=cm.
故答案为:3cm或7cm.
14. 劣弧 优弧
【解析】略
15.弦有:弦,弦,弦;优弧:,,,;劣弧:,,,
【解析】解:弦有:弦,弦,弦;优弧:,,,;劣弧:,,,.
16.平方厘米
【解析】解:根据题意,则
(平方厘米);
∴它的面积增加了125.6平方厘米.
17.28.26平方米
【解析】外圆半径r1为5米,围修一条宽1米的小路
∴内圆半径r2为4米
圆环的面积为
=πr12-πr22=3.14×5×5-3.14×4×4=78.5-50.24=28.26
∴小路的面积为28.26平方米.
18.所求图形为阴影部分(包括阴影的边界).
【解析】如图所示,以点A,B为圆心,3cm为半径画圆,两个圆相交的部分为阴影部分,图中阴影部分就是到点A和点B的距离都不大于3 cm的所有点组成的图形.
19.2个
【解析】解:这样的圆能画2个.如图:
作的垂直平分线,再以点为圆心,为半径作圆交于和,然后分别以和为圆心,以为半径作圆,
则和为所求圆.
20.当点P在OA上时PA<PC<PB,OB上时PB<PC<PA,当点P在点O处时PA=PB=PC.
【解析】当点P与点O重合时,PA=PB=PC,
当点P在OA上时,PA<PC<PB.
理由:连接OC,
在△POC中,OC-OP<PC<OP+OC,
∵OA=OB=OC,
∴OA-OP<PC<OP+OB,∴PA<PC<PB,
同理,当P点在OB上时,PB<PC<PA.
21.(1)相等;(2)相等.
【解析】(1)BC=AB-AC=10,
甲所走的路径长= 2 π = 2 π =20π(m),
乙所走的路径长= 2 π + 2 π = 2 π + π =20π(m),
所以两人所走路程的相等;
(2)两人走的路程远近相同.理由如下:甲所走的路径长= 2 π =π AB,
乙所走的路径长= 2 π + 2 π + π =π(AC+CD+DB)=π AB,
即两人走的路程远近相同.
22.(1)约;(2)约
【解析】解:(1)根据题意得:内圈弯道半径为 (米),
答:内圈弯道半径约为;
(2)由(1)得:外圈弯道半径为 (米),
一个内圈弯道与一个外圈弯道的长相差为 (米),
答:一个内圈弯道与一个外圈弯道的长相差约.答案第1页,共2页
答案第1页,共2页
同课章节目录
