24.1.2垂直于线的直径-同步练习 2021-2022学年人教版九年级数学上册(Word版含解析)
文档属性
| 名称 | 24.1.2垂直于线的直径-同步练习 2021-2022学年人教版九年级数学上册(Word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 667.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-01 00:00:00 | ||
图片预览



文档简介
2021-2022学年九年级数学上册(人教版)教材同步
24.1.2垂直于线的直径-同步练习
时间:60分钟
一、单选题
1.如图,半圆的直径,为圆心,为的中点,,交于点,则弦的长为( )
A. B. C. D.
2.已知的半径为,弦,则和的距离为( )
A. B. C.或 D.或
3.下列说法正确的是( )
A.垂直于弦的直线平分弦所对的两条弧 B.平分弦的直径垂直于弦
C.垂直于直径的弦平分这条直径 D.弦的垂直平分线经过圆心
4.下列说法中错误的有( )
①过弦的中点的直线平分弦所对的两条弧;
②弦的垂线平分它所对的两条弧;
③过弦的中点的直径平分弦所对的两条弧;
④平分不是直径的弦的直径平分弦所对的两条弧.
A.1个 B.2个 C.3个 D.4个
5.如图所示,点M是半径为5的内一点,且OM=3,在过点M的所有的弦中,弦长为整数的弦的条数为( )
A.2 B.3 C.4 D.5
6.如图,AB是所对的弦,AB的垂直平分线CD分别交于C,交AB于D,AD的垂直平分线EF分别交于E,交AB于F,DB的垂直平分线GH分别交于G,交AB于H,下列结论中不正确的是( )
A. B. C. D.EF=GH
7.如图,AB是⊙O的弦,OD⊥AB于D交⊙O于E,则下列说法错误的是( )
A.AD=BD B.∠ACB=∠AOE C.弧AE=弧BE D.OD=DE
8.“圆材埋壁”是我国古代著名数学著作《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”此问题即:“如图所示,CD垂直平分弦AB,CD=1寸,AB=10寸,求圆的直径”(1尺=10寸)根据题意直径长为( )
A.10寸 B.20寸
C.13寸 D.26寸
二、填空题
9.如图是由两个长方形组成的工件平面图(单位:mm),直线l是它的对称轴,若HG=60,AB=80,GF=50,CB=20,能完全覆盖这个平面图形的圆面的最小半径是__________mm.
10.如图,在⊙O中,直径AB=6,BC是弦,∠ABC=30°,点P在BC上,点Q在⊙O上,且OP⊥PQ,当点P在BC上移动时,则PQ长的最大值为__________.
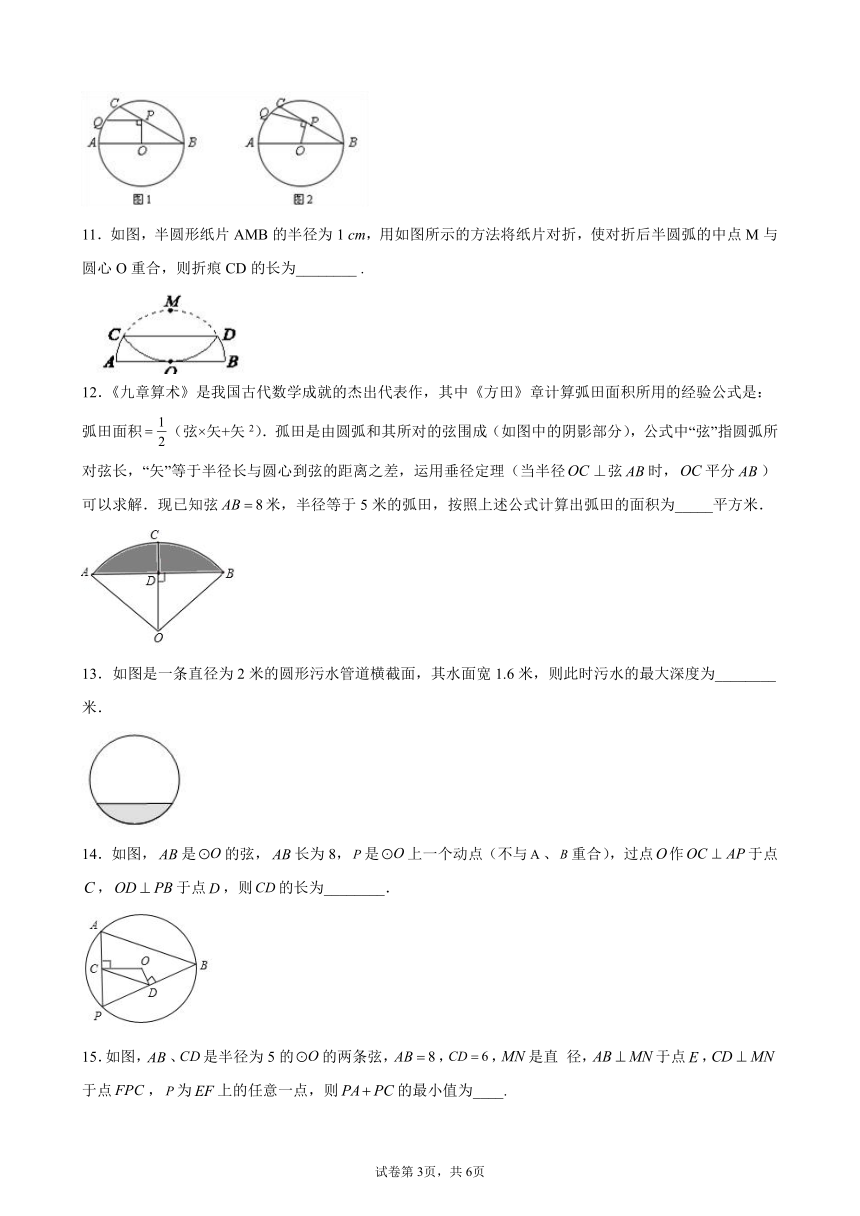
11.如图,半圆形纸片AMB的半径为1 cm,用如图所示的方法将纸片对折,使对折后半圆弧的中点M与圆心O重合,则折痕CD的长为________ .
12.《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章计算弧田面积所用的经验公式是:弧田面积(弦×矢+矢2).孤田是由圆弧和其所对的弦围成(如图中的阴影部分),公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,运用垂径定理(当半径⊥弦时,平分)可以求解.现已知弦米,半径等于5米的弧田,按照上述公式计算出弧田的面积为_____平方米.
13.如图是一条直径为2米的圆形污水管道横截面,其水面宽1.6米,则此时污水的最大深度为________米.
14.如图,是的弦,长为8,是上一个动点(不与、重合),过点作于点,于点,则的长为________.
15.如图,、是半径为5的的两条弦,,,是直 径,于点,于点,为上的任意一点,则的最小值为____.
16.如图,在⊙O中,如果,那么AB=_____,∠AOB=∠______,若OE⊥AB于E,OF⊥CD于F,则OE ______OF。
三、解答题
17.已知:如图,试用尺规将它四等分.
18.如图,所在的直线垂直平分线段,利用这样的工具,最少使用多少次,就可以找到圆形工件的圆心?为什么?
19.一辆卡车裝满货物后,它的高比宽多,且恰好通过如图所示的隧道(上部为半圆形).卡车有多高?(结果精确到)
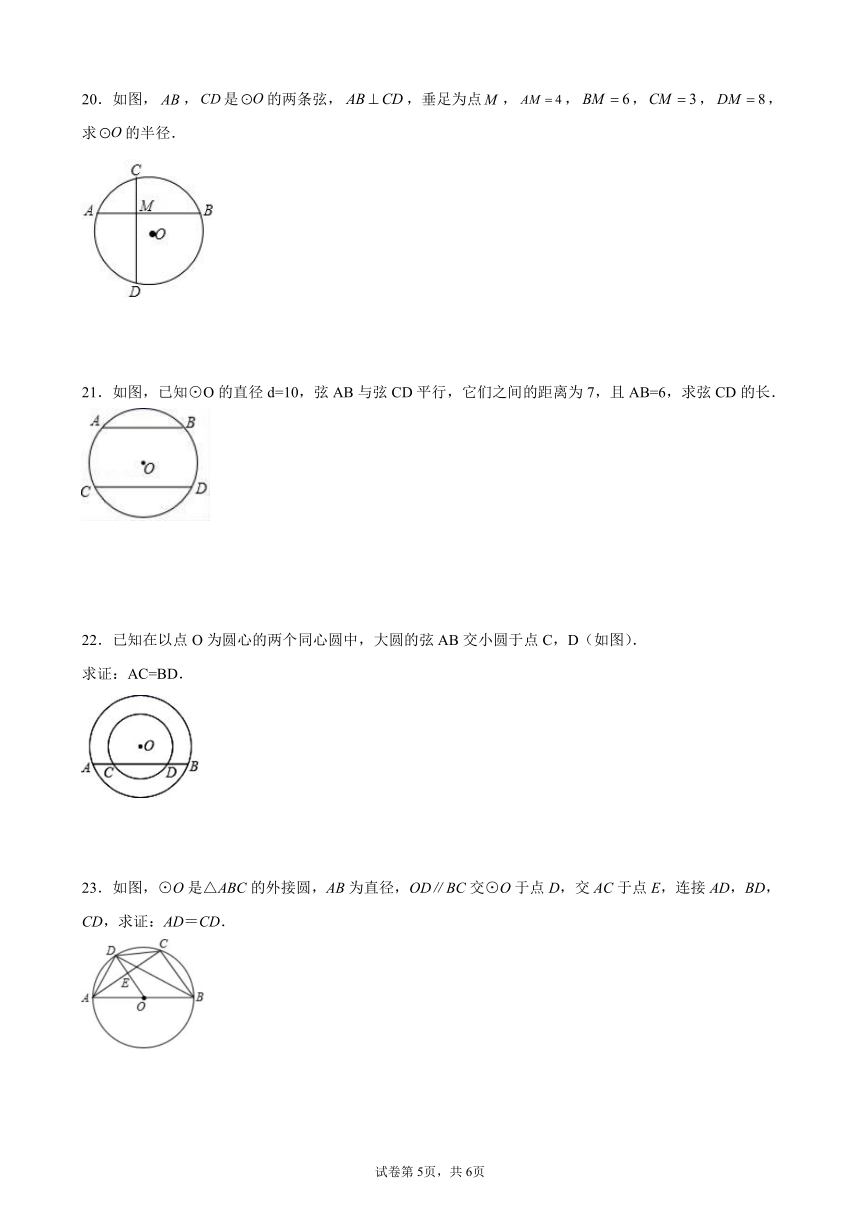
20.如图,,是的两条弦,,垂足为点,,,,,求的半径.
21.如图,已知⊙O的直径d=10,弦AB与弦CD平行,它们之间的距离为7,且AB=6,求弦CD的长.
22.已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).
求证:AC=BD.
23.如图,⊙O是△ABC的外接圆,AB为直径,OD∥BC交⊙O于点D,交AC于点E,连接AD,BD,CD,求证:AD=CD.
24.赵州桥如图是我国隋代建造的石拱桥,距今约有1400年的历史,是我国古代人民勤劳与智慧的结晶.它的主桥拱是圆弧形,它的跨度(弧所对的弦的长)为,拱高(弧的中点到弦的距离)为,求赵州桥主桥拱的半径(结果保留小数点后一位).
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.A
【解析】解:如图所示,连接,
∵,,
∴,
∴,即.
∵,
∴,
∵为的中点,
∴,
在中,,,
∴,
∴.
故选A.
2.C
【解析】解:如图1,
当、在圆心的同侧时,连接、,过作于,交于,
,
,
,,
,,
,
,
,
;
如图2,当、在圆心的异侧时,连接、,过作于,反向延长交于,
,
,
,,
,,
,
,
,
;
故选:.
3.D
【解析】解:A.垂直于弦的直径平分弦所对的两条弧,所以A选项错误;
B.平分弦(非直径)的直径垂直于弦,所以B选项错误;
C.垂直于直径的弦被这条直径平分,所以C选项错误;
D.弦的垂直平分线经过圆心,所以D选项正确.
故选D.
4.C
【解析】①中若直线与弦不垂直,则结论不成立;
②若垂线不是直径,则结论不成立;
③若所过的弦中点故选:C所在的弦本身就是直径,则结论不成立.
故①②③都不正确,④正确.
故选:C
5.C
【解析】如图,OM⊥AB,那么AB是过M的最短的弦,过M的最长的弦是圆的直径,
在Rt△AMO中,AM=AB,OA=5,OM=3,
∴AM=4,
∴AB=8,
∴过M所有O的弦中,最短的弦长度为8,最长的弦长度为10,
∴弦的长度可以分别为8、9、10,
当弦长为8、10时,过M点的弦分别为弦AB和过M点的直径,分别有一条;
而圆是轴对称图形,当弦长为9时,根据圆的对称性知,符合条件的弦应该有两条;
∴弦长为整数的弦的条数为4,一条长度8,一条长度为10,两条长度为9.
故选C.
6.C
【解析】作出圆心O,连接OE、OG,过O作MN∥FH交EF于M,交GH于N.
∵AB的中垂线CD分别交弧AB于C,∴弧AC=弧CB,故A正确;
∵FH⊥EF,FH⊥GH,CD⊥FH,∴EF∥GH∥CD,∴∠MEO=∠EOC,∠NGO=∠GOC.
∵MN∥FH,∴∠EMO=∠GNO=90°,∠EMO=∠MFD=∠FDO=90°,∴四边形FDOM是矩形,∴FM=DO,FD=MO.
同理可证:OD=HN,DH=ON.
∴FM=DO=HN.
∵FD=AD=DB=DH,∴MO=NO.
∵EO=GO,∴Rt△EMO≌Rt△GNO,∴EM=GN,∠MEO=∠NGO.
∵FM=DO=HN,EF=GH,故D正确;
∵∠MEO=∠EOC,∠NGO=∠GOC,∠MEO=∠NGO,∴∠EOC=∠GOC,∴弧EC=弧CG,故B正确;
过E作EP⊥CD于P,连接EC,AE,ED.
∵EF是AD的中垂线,∴AE=ED.
下面证明一般情况下,EC≠ED.
假设EC=ED.
∵EP⊥CD,∴CP=PD.
易证四边形EFDP是矩形,∴PD=EF,∴CD=2EF,从已知不能得出这个结论.故EC=ED是错误的,∴EC≠ED,∴AE≠EC,∴弧AE≠弧EC,故C错误.
故选C.
7.D
【解析】∵OD⊥AB,∴由垂径定理知,点D是AB的中点,有AD=BD,=,∴△AOB是等腰三角形,OD是∠AOB的平分线,有∠AOE=12∠AOB,由圆周角定理知,∠C=12∠AOB,∴∠ACB=∠AOE,故A、 B、C正确,而点D不一定是OE的中点,故错误.故选D.
8.D
【解析】解:连接OD,OA,
∵CD垂直平分弦AB,CD=1寸,AB=10寸,
∴AD=5寸,
在Rt△OAD中,OA2=OD2+AD2,
即OA2=(OA 1)2+52,
解得:OA=13,
故圆的直径为26寸,
故选D.
9.50
【解析】如图,设圆心为O,连接AO,CO,
∵直线l是它的对称轴,
∴CM=30,AN=40,
∵CM2+OM2=AN2+ON2,
∴302+OM2=402+(70-OM)2,
解得:OM=40,
∴OC==50,
∴能完全覆盖这个平面图形的圆面的最小半径是50mm.
故答案为50.
10.
【解析】如图3,连接OQ,∵在⊙O中,直径AB=6,OP⊥PQ,
∴OQ=OB=3,∠OPQ=90°,
∴PQ=,
∴当OP最短时,PQ就最长.
∵点O是定点,点P是线段BC上的动点,
∴如图4,当OP⊥BC于点P时,OP最短,此时,点Q与点C重合,
∵OP⊥BC,∠ABC=30°,
∴OP=OB=,
∴此时,PQ=.
即PQ的最长值为:.
11.cm
【解析】作MO交CD于E,则MO⊥CD,连接CO,
对折后半圆弧的中点M与圆心O重合,
则ME=OE=OC,
在直角三角形COE中,CE=,
折痕CD的长为2×=(cm).
故答案为cm
12.10
【解析】解:∵弦米,半径弦,
∴,
∴,
∴,
∴弧田面积(弦×矢+矢2),
故答案为10
13.0.4
【解析】如图,连接,过点作于点,
∵,米,
∴(米),
∵圆形污水管道的直径为2米,
∴米,
在中,根据勾股定理得,(米),
∴(米).
故答案是0.4.
14.4
【解析】解:∵,,
∴,,
∴是的中位线,
∴.
故答案为:4.
15..
【解析】连接OA,OB,OC,作CH垂直于AB于H.
根据垂径定理,得到BE=
∴CH=OE+OF=3+4=7,
BH=BE+EH=BE+CF=4+3=7,
在直角△BCH中根据勾股定理得到BC=7,
则PA+PC的最小值为7.
16.CD COD =
【解析】∵=,
∴AB=CD,∠AOB=∠DOC,
∵AO=DO,BO=CO,∠AOB=∠DOC,
∴△AOB≌△DOC,
∵OE、OF均为对应边上的高,
∴OE=OF.
17.见解析
【解析】解:如图所示,点、、把四等分.
18.最少用2次,见解析
【解析】解:如图所示,根据垂径定理的推论,两个直径的交点即为圆心.
故最少使用2次就可以找到圆形工件的圆心.
19.约
【解析】解:设该卡车的宽是x米,高是(x+2)米.
如图,设半圆O的半径为R,则R=2.5米,
作弦EF∥AD,且EF=x米,OH⊥EF于H,
连接OF,
由OH⊥EF,得HF=x米,
在Rt△OHF中,米,
则OH+4=x+2,即+4=x+2,
整理得 5x2-16x-9=0,
解得 (舍去),
则该卡车的高度为:(米).
答:卡车的高度大约是5.7m.
20.的半径为
【解析】解:如图,作于,于,连接,
则,,
∵,,,,
∴,,
∴,,
∴,
∵,,,
∴四边形是矩形,
∴,
在中,,即的半径为.
21.8
【解析】作OM⊥AB于M,ON⊥CD于N,连接OA、OC,
则
∵AB∥CD,
∴点M、O、N在同一条直线上,
在Rt△AOM中,
∴ON=MN﹣OM=3,
在Rt△CON中,
∵ON⊥CD,
∴CD=2CN=8.
22.证明见解析.
【解析】过O作OE⊥AB于点E,
则CE=DE,AE=BE,
∴BE-DE=AE-CE.
即AC=BD.
23.详见解析.
【解析】证明:连接OC,
∵OD∥BC,
∴∠ODB=∠CBD,
又OB=OD,
∴∠ODB=∠OBD,
∴∠OBD=∠CBD,
∵∠AOD=2∠OBD,∠DOC=2∠CBD,
∴∠AOD=∠DOC,
∴AD=CD.
24.27.3m
【解析】解:如图,用表示主桥拱,设所在圆的圆心为O,半径为R,经过圆心O作弦的垂线为垂足,与相交于点C,连接,根据垂径定理,D是的中点,C是的中点,就是拱高,
由题设可知,
所以,
,
在中,由勾股定理,得,
即,
解得.
因此,赵州桥的主桥拱半径约为.
答案第1页,共2页
答案第1页,共2页
24.1.2垂直于线的直径-同步练习
时间:60分钟
一、单选题
1.如图,半圆的直径,为圆心,为的中点,,交于点,则弦的长为( )
A. B. C. D.
2.已知的半径为,弦,则和的距离为( )
A. B. C.或 D.或
3.下列说法正确的是( )
A.垂直于弦的直线平分弦所对的两条弧 B.平分弦的直径垂直于弦
C.垂直于直径的弦平分这条直径 D.弦的垂直平分线经过圆心
4.下列说法中错误的有( )
①过弦的中点的直线平分弦所对的两条弧;
②弦的垂线平分它所对的两条弧;
③过弦的中点的直径平分弦所对的两条弧;
④平分不是直径的弦的直径平分弦所对的两条弧.
A.1个 B.2个 C.3个 D.4个
5.如图所示,点M是半径为5的内一点,且OM=3,在过点M的所有的弦中,弦长为整数的弦的条数为( )
A.2 B.3 C.4 D.5
6.如图,AB是所对的弦,AB的垂直平分线CD分别交于C,交AB于D,AD的垂直平分线EF分别交于E,交AB于F,DB的垂直平分线GH分别交于G,交AB于H,下列结论中不正确的是( )
A. B. C. D.EF=GH
7.如图,AB是⊙O的弦,OD⊥AB于D交⊙O于E,则下列说法错误的是( )
A.AD=BD B.∠ACB=∠AOE C.弧AE=弧BE D.OD=DE
8.“圆材埋壁”是我国古代著名数学著作《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”此问题即:“如图所示,CD垂直平分弦AB,CD=1寸,AB=10寸,求圆的直径”(1尺=10寸)根据题意直径长为( )
A.10寸 B.20寸
C.13寸 D.26寸
二、填空题
9.如图是由两个长方形组成的工件平面图(单位:mm),直线l是它的对称轴,若HG=60,AB=80,GF=50,CB=20,能完全覆盖这个平面图形的圆面的最小半径是__________mm.
10.如图,在⊙O中,直径AB=6,BC是弦,∠ABC=30°,点P在BC上,点Q在⊙O上,且OP⊥PQ,当点P在BC上移动时,则PQ长的最大值为__________.
11.如图,半圆形纸片AMB的半径为1 cm,用如图所示的方法将纸片对折,使对折后半圆弧的中点M与圆心O重合,则折痕CD的长为________ .
12.《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章计算弧田面积所用的经验公式是:弧田面积(弦×矢+矢2).孤田是由圆弧和其所对的弦围成(如图中的阴影部分),公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,运用垂径定理(当半径⊥弦时,平分)可以求解.现已知弦米,半径等于5米的弧田,按照上述公式计算出弧田的面积为_____平方米.
13.如图是一条直径为2米的圆形污水管道横截面,其水面宽1.6米,则此时污水的最大深度为________米.
14.如图,是的弦,长为8,是上一个动点(不与、重合),过点作于点,于点,则的长为________.
15.如图,、是半径为5的的两条弦,,,是直 径,于点,于点,为上的任意一点,则的最小值为____.
16.如图,在⊙O中,如果,那么AB=_____,∠AOB=∠______,若OE⊥AB于E,OF⊥CD于F,则OE ______OF。
三、解答题
17.已知:如图,试用尺规将它四等分.
18.如图,所在的直线垂直平分线段,利用这样的工具,最少使用多少次,就可以找到圆形工件的圆心?为什么?
19.一辆卡车裝满货物后,它的高比宽多,且恰好通过如图所示的隧道(上部为半圆形).卡车有多高?(结果精确到)
20.如图,,是的两条弦,,垂足为点,,,,,求的半径.
21.如图,已知⊙O的直径d=10,弦AB与弦CD平行,它们之间的距离为7,且AB=6,求弦CD的长.
22.已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).
求证:AC=BD.
23.如图,⊙O是△ABC的外接圆,AB为直径,OD∥BC交⊙O于点D,交AC于点E,连接AD,BD,CD,求证:AD=CD.
24.赵州桥如图是我国隋代建造的石拱桥,距今约有1400年的历史,是我国古代人民勤劳与智慧的结晶.它的主桥拱是圆弧形,它的跨度(弧所对的弦的长)为,拱高(弧的中点到弦的距离)为,求赵州桥主桥拱的半径(结果保留小数点后一位).
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.A
【解析】解:如图所示,连接,
∵,,
∴,
∴,即.
∵,
∴,
∵为的中点,
∴,
在中,,,
∴,
∴.
故选A.
2.C
【解析】解:如图1,
当、在圆心的同侧时,连接、,过作于,交于,
,
,
,,
,,
,
,
,
;
如图2,当、在圆心的异侧时,连接、,过作于,反向延长交于,
,
,
,,
,,
,
,
,
;
故选:.
3.D
【解析】解:A.垂直于弦的直径平分弦所对的两条弧,所以A选项错误;
B.平分弦(非直径)的直径垂直于弦,所以B选项错误;
C.垂直于直径的弦被这条直径平分,所以C选项错误;
D.弦的垂直平分线经过圆心,所以D选项正确.
故选D.
4.C
【解析】①中若直线与弦不垂直,则结论不成立;
②若垂线不是直径,则结论不成立;
③若所过的弦中点故选:C所在的弦本身就是直径,则结论不成立.
故①②③都不正确,④正确.
故选:C
5.C
【解析】如图,OM⊥AB,那么AB是过M的最短的弦,过M的最长的弦是圆的直径,
在Rt△AMO中,AM=AB,OA=5,OM=3,
∴AM=4,
∴AB=8,
∴过M所有O的弦中,最短的弦长度为8,最长的弦长度为10,
∴弦的长度可以分别为8、9、10,
当弦长为8、10时,过M点的弦分别为弦AB和过M点的直径,分别有一条;
而圆是轴对称图形,当弦长为9时,根据圆的对称性知,符合条件的弦应该有两条;
∴弦长为整数的弦的条数为4,一条长度8,一条长度为10,两条长度为9.
故选C.
6.C
【解析】作出圆心O,连接OE、OG,过O作MN∥FH交EF于M,交GH于N.
∵AB的中垂线CD分别交弧AB于C,∴弧AC=弧CB,故A正确;
∵FH⊥EF,FH⊥GH,CD⊥FH,∴EF∥GH∥CD,∴∠MEO=∠EOC,∠NGO=∠GOC.
∵MN∥FH,∴∠EMO=∠GNO=90°,∠EMO=∠MFD=∠FDO=90°,∴四边形FDOM是矩形,∴FM=DO,FD=MO.
同理可证:OD=HN,DH=ON.
∴FM=DO=HN.
∵FD=AD=DB=DH,∴MO=NO.
∵EO=GO,∴Rt△EMO≌Rt△GNO,∴EM=GN,∠MEO=∠NGO.
∵FM=DO=HN,EF=GH,故D正确;
∵∠MEO=∠EOC,∠NGO=∠GOC,∠MEO=∠NGO,∴∠EOC=∠GOC,∴弧EC=弧CG,故B正确;
过E作EP⊥CD于P,连接EC,AE,ED.
∵EF是AD的中垂线,∴AE=ED.
下面证明一般情况下,EC≠ED.
假设EC=ED.
∵EP⊥CD,∴CP=PD.
易证四边形EFDP是矩形,∴PD=EF,∴CD=2EF,从已知不能得出这个结论.故EC=ED是错误的,∴EC≠ED,∴AE≠EC,∴弧AE≠弧EC,故C错误.
故选C.
7.D
【解析】∵OD⊥AB,∴由垂径定理知,点D是AB的中点,有AD=BD,=,∴△AOB是等腰三角形,OD是∠AOB的平分线,有∠AOE=12∠AOB,由圆周角定理知,∠C=12∠AOB,∴∠ACB=∠AOE,故A、 B、C正确,而点D不一定是OE的中点,故错误.故选D.
8.D
【解析】解:连接OD,OA,
∵CD垂直平分弦AB,CD=1寸,AB=10寸,
∴AD=5寸,
在Rt△OAD中,OA2=OD2+AD2,
即OA2=(OA 1)2+52,
解得:OA=13,
故圆的直径为26寸,
故选D.
9.50
【解析】如图,设圆心为O,连接AO,CO,
∵直线l是它的对称轴,
∴CM=30,AN=40,
∵CM2+OM2=AN2+ON2,
∴302+OM2=402+(70-OM)2,
解得:OM=40,
∴OC==50,
∴能完全覆盖这个平面图形的圆面的最小半径是50mm.
故答案为50.
10.
【解析】如图3,连接OQ,∵在⊙O中,直径AB=6,OP⊥PQ,
∴OQ=OB=3,∠OPQ=90°,
∴PQ=,
∴当OP最短时,PQ就最长.
∵点O是定点,点P是线段BC上的动点,
∴如图4,当OP⊥BC于点P时,OP最短,此时,点Q与点C重合,
∵OP⊥BC,∠ABC=30°,
∴OP=OB=,
∴此时,PQ=.
即PQ的最长值为:.
11.cm
【解析】作MO交CD于E,则MO⊥CD,连接CO,
对折后半圆弧的中点M与圆心O重合,
则ME=OE=OC,
在直角三角形COE中,CE=,
折痕CD的长为2×=(cm).
故答案为cm
12.10
【解析】解:∵弦米,半径弦,
∴,
∴,
∴,
∴弧田面积(弦×矢+矢2),
故答案为10
13.0.4
【解析】如图,连接,过点作于点,
∵,米,
∴(米),
∵圆形污水管道的直径为2米,
∴米,
在中,根据勾股定理得,(米),
∴(米).
故答案是0.4.
14.4
【解析】解:∵,,
∴,,
∴是的中位线,
∴.
故答案为:4.
15..
【解析】连接OA,OB,OC,作CH垂直于AB于H.
根据垂径定理,得到BE=
∴CH=OE+OF=3+4=7,
BH=BE+EH=BE+CF=4+3=7,
在直角△BCH中根据勾股定理得到BC=7,
则PA+PC的最小值为7.
16.CD COD =
【解析】∵=,
∴AB=CD,∠AOB=∠DOC,
∵AO=DO,BO=CO,∠AOB=∠DOC,
∴△AOB≌△DOC,
∵OE、OF均为对应边上的高,
∴OE=OF.
17.见解析
【解析】解:如图所示,点、、把四等分.
18.最少用2次,见解析
【解析】解:如图所示,根据垂径定理的推论,两个直径的交点即为圆心.
故最少使用2次就可以找到圆形工件的圆心.
19.约
【解析】解:设该卡车的宽是x米,高是(x+2)米.
如图,设半圆O的半径为R,则R=2.5米,
作弦EF∥AD,且EF=x米,OH⊥EF于H,
连接OF,
由OH⊥EF,得HF=x米,
在Rt△OHF中,米,
则OH+4=x+2,即+4=x+2,
整理得 5x2-16x-9=0,
解得 (舍去),
则该卡车的高度为:(米).
答:卡车的高度大约是5.7m.
20.的半径为
【解析】解:如图,作于,于,连接,
则,,
∵,,,,
∴,,
∴,,
∴,
∵,,,
∴四边形是矩形,
∴,
在中,,即的半径为.
21.8
【解析】作OM⊥AB于M,ON⊥CD于N,连接OA、OC,
则
∵AB∥CD,
∴点M、O、N在同一条直线上,
在Rt△AOM中,
∴ON=MN﹣OM=3,
在Rt△CON中,
∵ON⊥CD,
∴CD=2CN=8.
22.证明见解析.
【解析】过O作OE⊥AB于点E,
则CE=DE,AE=BE,
∴BE-DE=AE-CE.
即AC=BD.
23.详见解析.
【解析】证明:连接OC,
∵OD∥BC,
∴∠ODB=∠CBD,
又OB=OD,
∴∠ODB=∠OBD,
∴∠OBD=∠CBD,
∵∠AOD=2∠OBD,∠DOC=2∠CBD,
∴∠AOD=∠DOC,
∴AD=CD.
24.27.3m
【解析】解:如图,用表示主桥拱,设所在圆的圆心为O,半径为R,经过圆心O作弦的垂线为垂足,与相交于点C,连接,根据垂径定理,D是的中点,C是的中点,就是拱高,
由题设可知,
所以,
,
在中,由勾股定理,得,
即,
解得.
因此,赵州桥的主桥拱半径约为.
答案第1页,共2页
答案第1页,共2页
同课章节目录
