24.4弧长和扇形面积 同步练习 2021-2022学年人教版九年级数学上册 (Word版含解析)
文档属性
| 名称 | 24.4弧长和扇形面积 同步练习 2021-2022学年人教版九年级数学上册 (Word版含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 464.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-01 11:57:05 | ||
图片预览





文档简介
2021-2022学年九年级数学上册(人教版)教材同步
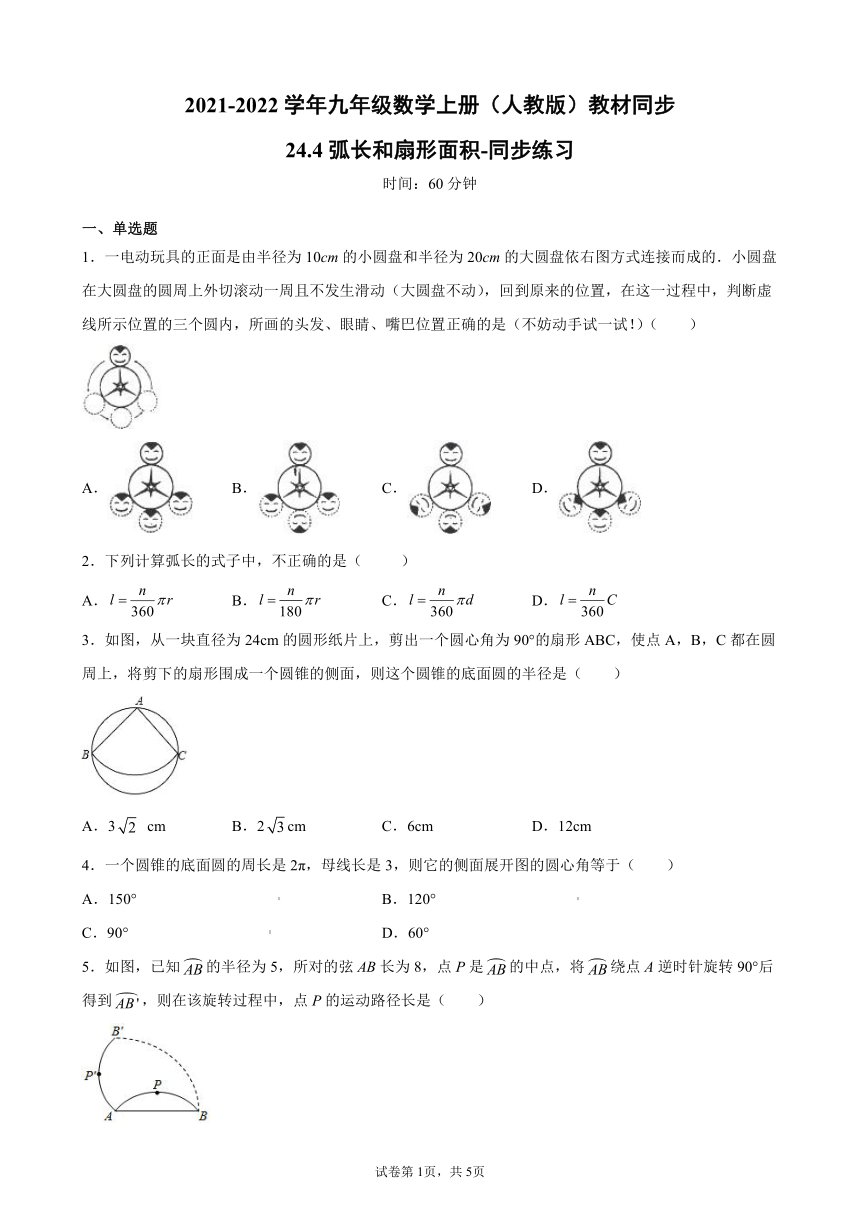
24.4弧长和扇形面积-同步练习
时间:60分钟
一、单选题
1.一电动玩具的正面是由半径为10cm的小圆盘和半径为20cm的大圆盘依右图方式连接而成的.小圆盘在大圆盘的圆周上外切滚动一周且不发生滑动(大圆盘不动),回到原来的位置,在这一过程中,判断虚线所示位置的三个圆内,所画的头发、眼睛、嘴巴位置正确的是(不妨动手试一试!)( )
A. B. C. D.
2.下列计算弧长的式子中,不正确的是( )
A. B. C. D.
3.如图,从一块直径为24cm的圆形纸片上,剪出一个圆心角为90°的扇形ABC,使点A,B,C都在圆周上,将剪下的扇形围成一个圆锥的侧面,则这个圆锥的底面圆的半径是( )
A.3 cm B.2cm C.6cm D.12cm
4.一个圆锥的底面圆的周长是2π,母线长是3,则它的侧面展开图的圆心角等于( )
A.150° B.120°
C.90° D.60°
5.如图,已知的半径为5,所对的弦AB长为8,点P是的中点,将绕点A逆时针旋转90°后得到,则在该旋转过程中,点P的运动路径长是( )
A.π B.π C.2π D.2π
6.若半径为6的圆中,扇形面积为,则它的弧长为( ).
A. B. C. D.
7.如图,在Rt中,∠BCA=90° 两分圆别以为半径画圆,则阴影部分的面积为( )
A. B. C. D.
8.如图,圆锥的底面半径为2,母线长为6,则侧面积为( )
A.4π B.6π C.12π D.16π
二、填空题
9.用一块半径为4,圆心角为90°的扇形纸片围成一个圆锥的侧面,则此圆锥的高为_____.
10.圆锥的底面半径为1cm,母线长为3cm,则它的侧面展开图的圆心角的度数等于 ______;
11.一个圆锥截成圆台,已知圆台的上下底面半径的比是1∶4,母线长为10cm,求圆锥的母线长____.
12.已知圆锥的母线长OA=8,底面圆的半径r=2,若一只小虫从点A出发,绕圆锥的侧面爬行一周后又回到A点,则小虫爬行的最短路线的长是____(结果保留根号).
13.半径为2㎝,圆心角为90°的弧长为___________ .
14.75°的圆心角所对的弧长是2.5cm,则此弧所在圆的半径是_____cm.
15.半径为的圆中,长为的一条弧所对的圆心角的度数为_______.
16.如图,从一块半径为的圆形铁皮上剪出一个圆周角为120°的扇形,如果将剪下来的扇形围成一个圆锥,则该圆锥的底面圆的半径为_________.
三、解答题
17.如图,大半圆中有n个小半圆,大半圆的弧长为个小半圆的弧长和为,探索和的关系并证明你的结论.
18.如图,某家设计公司设计了这样一种纸扇:纸扇张开的最大角度与的比为黄金比,那么制作一把这样的纸扇至少要用多少平方厘米的纸?(纸扇有两面,结果精确到)
19.已知正方形的边长为2,求右图中阴影部分的面积.
20.如图,水平放置的一个油管的横截面半径为,其中有油的部分油面高,求截面上有油部分的面积(结果精确到).
21.中,.把它分别沿三边所在直线旋转一周.求所得三个几何体的全面积.
22.如图,ABCD是围墙,AB∥CD,∠ABC=120°,一根6m长的绳子,一端拴在围墙一角的柱子上(B处),另一端拴着一只羊(E处).
(1)请在图中画出羊活动的区域.
(2)求出羊活动区域的面积.
23.小明打算用一张半圆形的纸(如图)做一个圆锥.在制作过程中,他先将半圆剪成面积比为1∶2的两个扇形.
(1)请你在图中画出他的裁剪痕迹(要求尺规作图,不写作法,保留作图痕迹);
(2)若半圆半径是3,小明用裁出的大扇形作为圆锥的侧面,请你求出小明所做的圆锥的高.
24.如图,在一个半径为的圆形纸片中,剪一个圆心角为的扇形.
(1)求这个扇形的面积(保留);
(2)用所剪的纸片围成一个圆锥的侧面,求这个圆锥的底面圆的半径.
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.B
【解析】当小圆盘绕着大圆盘滚动一周时,小圆盘自转 +1=+1=3圈,
大圆盘内的三条长指针刚好把大圆盘的角度平分,
所以三条长指针所指的图象完全一致,故排除C、D.
相邻两根长指针所指的图象与其中间的图象肯定不一致,故排除A.
只有B符合.
故选:B.
2.A
【解析】,所以A不正确.
故选:A.
3.A
【解析】AB=cm,
∴
∴圆锥的底面圆的半径=÷(2π)=3cm.
故选A.
4.B
【解析】设圆锥的侧面展开图的圆心角为n°,
∵圆锥的底面圆的周长是2π,母线长是3,
∴2π=,
解得n=120.
故选B.
5.B
【解析】如图,设的圆心为O,连接OP交AB于C,连接OA,AP, AB′, AP′,
∵圆O半径为5,所对的弦AB长为8,点P是的中点,
根据垂径定理,得
AC=AB=4,PO⊥AB,
OC==3,
∴PC=OP﹣OC=5﹣3=2,
∴AP==2,
∵将绕点A逆时针旋转90°后得到,
∴∠PAP′=∠BAB′=90°,
∴LPP′==π.
则在该旋转过程中,点P的运动路径长是π.
故选:B.
6.B
【解析】根据扇形面积公式可知:,
∴弧长
故选:B.
7.A
【解析】设各个部分的面积为:S1、S2、S3、S4、S5,如图所示,
∵两个半圆的面积和是:S1+S5+S4+S2+S3+S4,△ABC的面积是S3+S4+S5,阴影部分
面积是:S1+S2+S4,
∴图中阴影部分的面积为两个半圆的面积减去三角形的面积.
即阴影部分的面积=π×4+π×1-4×2÷2=π-4.
故选A.
8.C
【解析】根据圆锥的侧面积公式:πrl=π×2×6=12π,
故选C.
9.
【解析】设圆锥的底面圆的半径为r,
根据题意得2πr=,解得r=1,
所以此圆锥的高=,
故答案为:.
10.120°
【解析】设圆心角为n,底面半径是1,
则底面周长
∴
故答案为:
11.cm
【解析】设圆锥的母线长为,圆台上、下底半径为.
故答案为:cm.
12.8
【解析】圆锥的侧面展开图,如图所示:∵圆锥的底面周长=2π×2=4π,
设侧面展开图的圆心角的度数为n.∴=4π,解得n=90,
∴最短路程为: =8.
故答案为8.
13.π cm
【解析】.
故答案为:π cm.
14.6
【解析】解:由题意得:圆的半径.
故本题答案为:6.
15.240°
【解析】解: 由题意得,解得n=240,
则长为的一条弧所对的圆心角的度数为.
故答案为:240°
16.
【解析】连接OA,OB,
则∠BAO=∠BAC==60°,
又∵OA=OB,
∴△AOB是等边三角形,
∴AB=OA=1,
∵∠BAC=120°,
∴的长为:,
设圆锥底面圆的半径为r
故答案为.
17.L1=L2,见解析
【解析】解:L1=L2,证明如下:
设n个小半圆的直径分别为d1,d2,d3,…dn,大半圆的直径为d大,
则有d1+d2+d3+…+dn=d大,
∴L2=(d1π+d2π+d3π+…+dnπ)=(d1+d2+d3+…+dn)π=d大π,
∵L1=d大π,
∴L1=L2.
18.约
【解析】解:∵θ与360°-θ的比为黄金比,
∴
解得:
∴所用纸的面积=cm2
19.2.28
【解析】解:根据题意,则
.
20.约
【解析】解:连接OA、OB,作OD⊥AB于C,交于D,
则AC=BC=AB,CD=6cm,
∴OC=OD CD=12cm 6cm=6cm,
∴OC=OA,
∴∠OAC=30°,
∵OA=OB,
∴∠OBC=∠OAC=30°,
∴∠AOB=180° 30° 30°=120°,AC=OC=6cm,
∴AB=2AC=12cm,
∴S阴影=S扇形OAB S△OAB=×6=48π 36≈88.4(cm2)
答:截面上有油部分的面积约为88.4 cm2.
21.所得三个几何体的全面积为76.8π.
【解析】解:∵中,;
∴;
过点C作CD⊥AB于点D,
SABC=BC·AC=AB·CD,
所以BC·AC=AB·CD,
所以CD===2.4,
①当沿AC所在直线旋转一周时,得到的是一个以BC为底面半径,AC为高,AB为母线的圆锥,此时圆锥的全面积是S=S侧+S底=AB·(2π·BC)+π·BC2=×5×(2π×4)+π×42=36π
②当沿 BC所在直线旋转一周时,得到的是一个以AC为底面半径,BC为高,AB为母线的圆锥,此时圆锥的全面积是S=S侧+S底=AB·(2π·AC)+π·AC2=×5×(2π×3)+π×32=24π
③当沿AB所在直线旋转一周时,得到的是一个复合几何体,这个几何体是由以AB边上的高线为底面半径的两个同底圆锥组成的,此时圆锥的全面积是S=S侧+S侧=AC·(2π·CD)+BC·(2π·CD)==BC·CD·π+ AC·CD·π=CD·π(BC+AC)=2.4π×(3+4)=16.8π
∴所得三个几何体的全面积S=36π+24π+16.8π=76.8π
22.(1)见解析;(2)
【解析】(1)如图所示:扇形MBN和扇形NCF即为所求;
(2)由题意可得:∠NCF=60°,MB=BN=6m,NC=2m,
羊活动区域的面积为:.
23.(1)见解析;(2)2
【解析】(1)如答图所示;
(2)∵半圆的半径为3,
∴半圆的弧长为3π,
∵剪成面积比为1∶2的两个扇形.
∴大扇形的弧长为2π,
设围成的圆锥的底面半径为r,则2πr=2π,
解得r=1,
∴圆锥的高为=2.
24.(1);(2)1
【解析】(1)如图,连接,∵,
∴为的直径,
∵为扇形,∵,
∴为等腰直角三角形,
∴
∴,
∴这个扇形的面积;
(2)设这个圆锥的底面圆的半径为,由题意得的长即为底面圆的周长
∵扇形中,的长,
∴,解得,即围成的这个圆锥的底面圆的半径为1.
答案第1页,共2页
答案第1页,共2页
24.4弧长和扇形面积-同步练习
时间:60分钟
一、单选题
1.一电动玩具的正面是由半径为10cm的小圆盘和半径为20cm的大圆盘依右图方式连接而成的.小圆盘在大圆盘的圆周上外切滚动一周且不发生滑动(大圆盘不动),回到原来的位置,在这一过程中,判断虚线所示位置的三个圆内,所画的头发、眼睛、嘴巴位置正确的是(不妨动手试一试!)( )
A. B. C. D.
2.下列计算弧长的式子中,不正确的是( )
A. B. C. D.
3.如图,从一块直径为24cm的圆形纸片上,剪出一个圆心角为90°的扇形ABC,使点A,B,C都在圆周上,将剪下的扇形围成一个圆锥的侧面,则这个圆锥的底面圆的半径是( )
A.3 cm B.2cm C.6cm D.12cm
4.一个圆锥的底面圆的周长是2π,母线长是3,则它的侧面展开图的圆心角等于( )
A.150° B.120°
C.90° D.60°
5.如图,已知的半径为5,所对的弦AB长为8,点P是的中点,将绕点A逆时针旋转90°后得到,则在该旋转过程中,点P的运动路径长是( )
A.π B.π C.2π D.2π
6.若半径为6的圆中,扇形面积为,则它的弧长为( ).
A. B. C. D.
7.如图,在Rt中,∠BCA=90° 两分圆别以为半径画圆,则阴影部分的面积为( )
A. B. C. D.
8.如图,圆锥的底面半径为2,母线长为6,则侧面积为( )
A.4π B.6π C.12π D.16π
二、填空题
9.用一块半径为4,圆心角为90°的扇形纸片围成一个圆锥的侧面,则此圆锥的高为_____.
10.圆锥的底面半径为1cm,母线长为3cm,则它的侧面展开图的圆心角的度数等于 ______;
11.一个圆锥截成圆台,已知圆台的上下底面半径的比是1∶4,母线长为10cm,求圆锥的母线长____.
12.已知圆锥的母线长OA=8,底面圆的半径r=2,若一只小虫从点A出发,绕圆锥的侧面爬行一周后又回到A点,则小虫爬行的最短路线的长是____(结果保留根号).
13.半径为2㎝,圆心角为90°的弧长为___________ .
14.75°的圆心角所对的弧长是2.5cm,则此弧所在圆的半径是_____cm.
15.半径为的圆中,长为的一条弧所对的圆心角的度数为_______.
16.如图,从一块半径为的圆形铁皮上剪出一个圆周角为120°的扇形,如果将剪下来的扇形围成一个圆锥,则该圆锥的底面圆的半径为_________.
三、解答题
17.如图,大半圆中有n个小半圆,大半圆的弧长为个小半圆的弧长和为,探索和的关系并证明你的结论.
18.如图,某家设计公司设计了这样一种纸扇:纸扇张开的最大角度与的比为黄金比,那么制作一把这样的纸扇至少要用多少平方厘米的纸?(纸扇有两面,结果精确到)
19.已知正方形的边长为2,求右图中阴影部分的面积.
20.如图,水平放置的一个油管的横截面半径为,其中有油的部分油面高,求截面上有油部分的面积(结果精确到).
21.中,.把它分别沿三边所在直线旋转一周.求所得三个几何体的全面积.
22.如图,ABCD是围墙,AB∥CD,∠ABC=120°,一根6m长的绳子,一端拴在围墙一角的柱子上(B处),另一端拴着一只羊(E处).
(1)请在图中画出羊活动的区域.
(2)求出羊活动区域的面积.
23.小明打算用一张半圆形的纸(如图)做一个圆锥.在制作过程中,他先将半圆剪成面积比为1∶2的两个扇形.
(1)请你在图中画出他的裁剪痕迹(要求尺规作图,不写作法,保留作图痕迹);
(2)若半圆半径是3,小明用裁出的大扇形作为圆锥的侧面,请你求出小明所做的圆锥的高.
24.如图,在一个半径为的圆形纸片中,剪一个圆心角为的扇形.
(1)求这个扇形的面积(保留);
(2)用所剪的纸片围成一个圆锥的侧面,求这个圆锥的底面圆的半径.
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.B
【解析】当小圆盘绕着大圆盘滚动一周时,小圆盘自转 +1=+1=3圈,
大圆盘内的三条长指针刚好把大圆盘的角度平分,
所以三条长指针所指的图象完全一致,故排除C、D.
相邻两根长指针所指的图象与其中间的图象肯定不一致,故排除A.
只有B符合.
故选:B.
2.A
【解析】,所以A不正确.
故选:A.
3.A
【解析】AB=cm,
∴
∴圆锥的底面圆的半径=÷(2π)=3cm.
故选A.
4.B
【解析】设圆锥的侧面展开图的圆心角为n°,
∵圆锥的底面圆的周长是2π,母线长是3,
∴2π=,
解得n=120.
故选B.
5.B
【解析】如图,设的圆心为O,连接OP交AB于C,连接OA,AP, AB′, AP′,
∵圆O半径为5,所对的弦AB长为8,点P是的中点,
根据垂径定理,得
AC=AB=4,PO⊥AB,
OC==3,
∴PC=OP﹣OC=5﹣3=2,
∴AP==2,
∵将绕点A逆时针旋转90°后得到,
∴∠PAP′=∠BAB′=90°,
∴LPP′==π.
则在该旋转过程中,点P的运动路径长是π.
故选:B.
6.B
【解析】根据扇形面积公式可知:,
∴弧长
故选:B.
7.A
【解析】设各个部分的面积为:S1、S2、S3、S4、S5,如图所示,
∵两个半圆的面积和是:S1+S5+S4+S2+S3+S4,△ABC的面积是S3+S4+S5,阴影部分
面积是:S1+S2+S4,
∴图中阴影部分的面积为两个半圆的面积减去三角形的面积.
即阴影部分的面积=π×4+π×1-4×2÷2=π-4.
故选A.
8.C
【解析】根据圆锥的侧面积公式:πrl=π×2×6=12π,
故选C.
9.
【解析】设圆锥的底面圆的半径为r,
根据题意得2πr=,解得r=1,
所以此圆锥的高=,
故答案为:.
10.120°
【解析】设圆心角为n,底面半径是1,
则底面周长
∴
故答案为:
11.cm
【解析】设圆锥的母线长为,圆台上、下底半径为.
故答案为:cm.
12.8
【解析】圆锥的侧面展开图,如图所示:∵圆锥的底面周长=2π×2=4π,
设侧面展开图的圆心角的度数为n.∴=4π,解得n=90,
∴最短路程为: =8.
故答案为8.
13.π cm
【解析】.
故答案为:π cm.
14.6
【解析】解:由题意得:圆的半径.
故本题答案为:6.
15.240°
【解析】解: 由题意得,解得n=240,
则长为的一条弧所对的圆心角的度数为.
故答案为:240°
16.
【解析】连接OA,OB,
则∠BAO=∠BAC==60°,
又∵OA=OB,
∴△AOB是等边三角形,
∴AB=OA=1,
∵∠BAC=120°,
∴的长为:,
设圆锥底面圆的半径为r
故答案为.
17.L1=L2,见解析
【解析】解:L1=L2,证明如下:
设n个小半圆的直径分别为d1,d2,d3,…dn,大半圆的直径为d大,
则有d1+d2+d3+…+dn=d大,
∴L2=(d1π+d2π+d3π+…+dnπ)=(d1+d2+d3+…+dn)π=d大π,
∵L1=d大π,
∴L1=L2.
18.约
【解析】解:∵θ与360°-θ的比为黄金比,
∴
解得:
∴所用纸的面积=cm2
19.2.28
【解析】解:根据题意,则
.
20.约
【解析】解:连接OA、OB,作OD⊥AB于C,交于D,
则AC=BC=AB,CD=6cm,
∴OC=OD CD=12cm 6cm=6cm,
∴OC=OA,
∴∠OAC=30°,
∵OA=OB,
∴∠OBC=∠OAC=30°,
∴∠AOB=180° 30° 30°=120°,AC=OC=6cm,
∴AB=2AC=12cm,
∴S阴影=S扇形OAB S△OAB=×6=48π 36≈88.4(cm2)
答:截面上有油部分的面积约为88.4 cm2.
21.所得三个几何体的全面积为76.8π.
【解析】解:∵中,;
∴;
过点C作CD⊥AB于点D,
SABC=BC·AC=AB·CD,
所以BC·AC=AB·CD,
所以CD===2.4,
①当沿AC所在直线旋转一周时,得到的是一个以BC为底面半径,AC为高,AB为母线的圆锥,此时圆锥的全面积是S=S侧+S底=AB·(2π·BC)+π·BC2=×5×(2π×4)+π×42=36π
②当沿 BC所在直线旋转一周时,得到的是一个以AC为底面半径,BC为高,AB为母线的圆锥,此时圆锥的全面积是S=S侧+S底=AB·(2π·AC)+π·AC2=×5×(2π×3)+π×32=24π
③当沿AB所在直线旋转一周时,得到的是一个复合几何体,这个几何体是由以AB边上的高线为底面半径的两个同底圆锥组成的,此时圆锥的全面积是S=S侧+S侧=AC·(2π·CD)+BC·(2π·CD)==BC·CD·π+ AC·CD·π=CD·π(BC+AC)=2.4π×(3+4)=16.8π
∴所得三个几何体的全面积S=36π+24π+16.8π=76.8π
22.(1)见解析;(2)
【解析】(1)如图所示:扇形MBN和扇形NCF即为所求;
(2)由题意可得:∠NCF=60°,MB=BN=6m,NC=2m,
羊活动区域的面积为:.
23.(1)见解析;(2)2
【解析】(1)如答图所示;
(2)∵半圆的半径为3,
∴半圆的弧长为3π,
∵剪成面积比为1∶2的两个扇形.
∴大扇形的弧长为2π,
设围成的圆锥的底面半径为r,则2πr=2π,
解得r=1,
∴圆锥的高为=2.
24.(1);(2)1
【解析】(1)如图,连接,∵,
∴为的直径,
∵为扇形,∵,
∴为等腰直角三角形,
∴
∴,
∴这个扇形的面积;
(2)设这个圆锥的底面圆的半径为,由题意得的长即为底面圆的周长
∵扇形中,的长,
∴,解得,即围成的这个圆锥的底面圆的半径为1.
答案第1页,共2页
答案第1页,共2页
同课章节目录
