信息窗2 正比例的意义(课件) 数学 六年级下册 青岛版(共36张PPT)
文档属性
| 名称 | 信息窗2 正比例的意义(课件) 数学 六年级下册 青岛版(共36张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-01 07:08:38 | ||
图片预览








文档简介
(共36张PPT)
正比例意义
青岛版数学六年级(下)
三 啤酒生产中的数学
——比 例
理解正比例的意义,能根据正比例的意义正确判断两种量是否成正比例。
认识正比例图像,能画出相应的正比例图像。
经历比较、分析、归纳等数学活动,提高分析比较和归纳概括能力,渗透函数思想。
【重点】
理解正比例的意义,会判断两种量是否成正比例。
【难点】
能画出相应的正比例图像,能根据
图像解决相关的实际问题。
0
0
1
15
2
30
3
45
4
60
5
90
6
75
7
105
……
……
工作时间
(时)
你能提出什么问题?
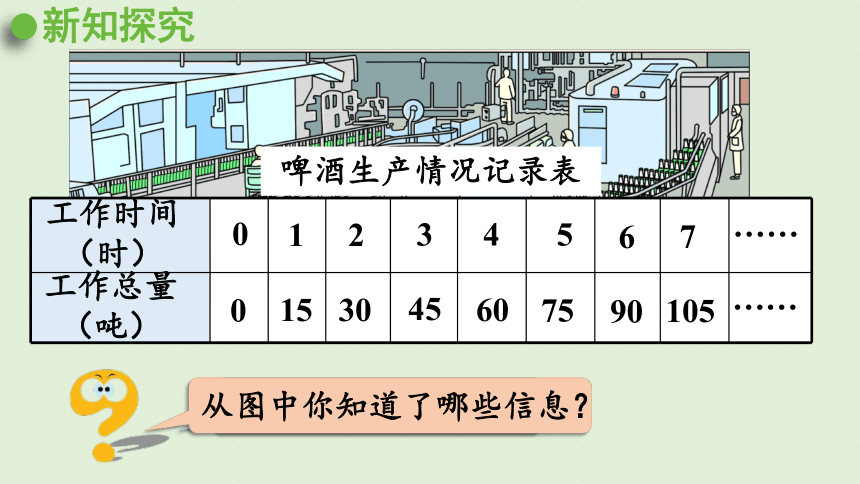
从图中你知道了哪些信息?
工作总量
(吨)
啤酒生产情况记录表
0
0
1
15
2
30
3
45
4
60
5
90
6
75
7
105
……
……
工作时间
(时)
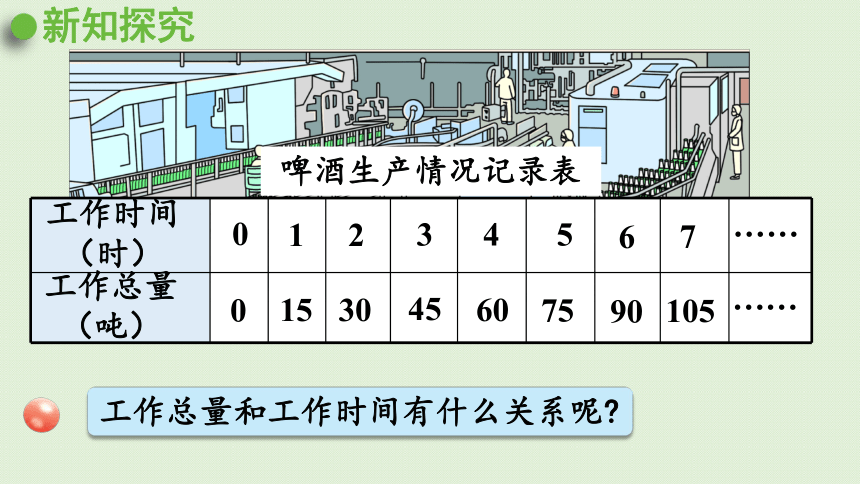
啤酒生产情况记录表
工作总量
(吨)
工作总量和工作时间有什么关系呢
0
0
1
15
2
30
3
45
4
60
5
90
6
75
7
105
……
工作时间
(时)
工作总量
(吨)
……
观察记录表,发现规律
工作总量与工作时间是两种相关联的量,工作总量是随着工作时间的变化而变化的。
工作时间越长,生产的啤酒越多;工作时间越短,生产的啤酒越少。
,……工作总量与工作时间的比值一定。
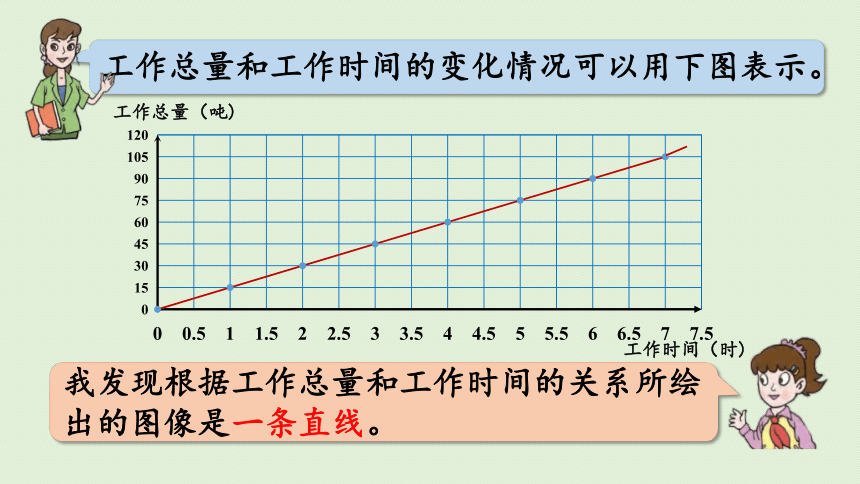
工作总量和工作时间的变化情况可以用下图表示。
我发现根据工作总量和工作时间的关系所绘出的图像是一条直线。
工作总量和工作时间的比值就是工作效率。用式子表示它们的关系:
=工作效率(一定)
用数量关系式表示工作总量和工作时间的关系
正比例的意义
工作总量和工作时间是两种相关联的量,工作时间变化,工作总量也随着变化。工作效率不变,也就是工作总量与工作时间的比值一定,我们就说工作总量和工作时间是成正比例的量,它们的关系叫作正比例关系。
用字母表示正比例关系
如果用字母x和y分别表示两种相关联的量,用k表示它们的比值(一定),正比例关系可以用下面的式子表示:
试一试
教材第43页“自主练习”第1题
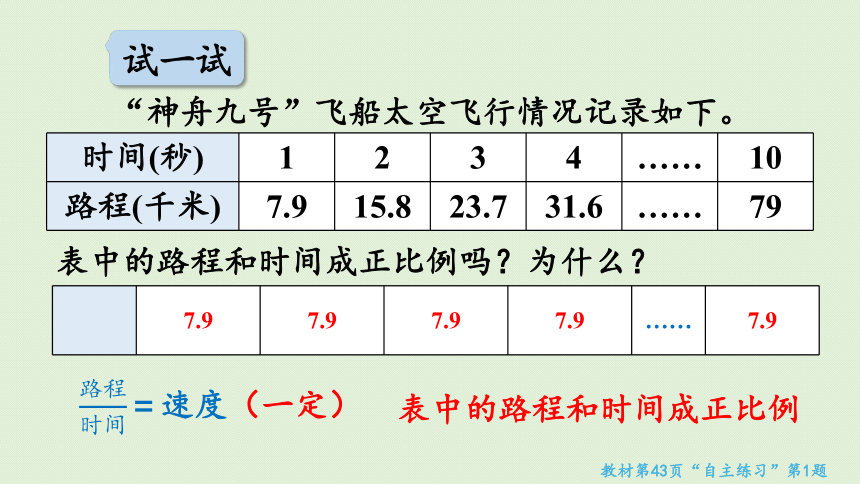
“神舟九号”飞船太空飞行情况记录如下。
时间(秒) 1 2 3 4 …… 10
路程(千米) 7.9 15.8 23.7 31.6 …… 79
表中的路程和时间成正比例吗?为什么?
7.9 7.9 7.9 7.9 …… 7.9
=速度(一定)
表中的路程和时间成正比例
以匀速行驶的汽车行驶的路程与行驶时间。
正方形的周长与它的边长。
圆的直径长度与它的半径长度。
想一想,生活中还有哪两种量成正比例关系?
下图是生产某种啤酒时,生产啤酒的总量与所需大麦芽吨数的关系。
横轴表示所需大麦芽的吨数,1个单位长度代表1吨
纵轴表示生产啤酒的总量,1个单位长度代表10吨
图像该怎么理解呢?
下图是生产某种啤酒时,生产啤酒的总量与所需大麦芽吨数的关系。
生产啤酒的总量对应的所需大麦芽的吨数都可以用图中的一个点表示,试一试。
1吨大麦芽生产10吨啤酒
可以用(1,10)表示
3吨大麦芽生产30吨啤酒
可以用(3,30)表示
下图是生产某种啤酒时,生产啤酒的总量与所需大麦芽吨数的关系。
(1)从图中你可以发现什么
①图像是一条经过原点的直线。
下图是生产某种啤酒时,生产啤酒的总量与所需大麦芽吨数的关系。
(1)从图中你可以发现什么
②生产啤酒总量和所需大麦芽吨数之间的变化规律:大麦芽的吨数越多,生产啤酒总量越多;大麦芽的吨数越少,生产啤酒总量越少。
下图是生产某种啤酒时,生产啤酒的总量与所需大麦芽吨数的关系。
(1)从图中你可以发现什么
③经过计算发现啤酒总量和大麦芽的吨数的比值一定,它们成正比例关系,这是一个正比例图像。正比例图像是一条通过原点的直线。
(2)根据此图说一说,用7吨大麦芽能生产多少吨啤酒
从图像中可以看出,用7吨大麦芽能生产70吨啤酒。
下图是生产某种啤酒时,生产啤酒的总量与所需大麦芽吨数的关系。
(3)估计一下,要生产95吨啤酒大约需要多少吨大麦芽
95
9.5
从图像中可以看出,要生产95吨啤酒大约需要9.5吨大芽。
下图是生产某种啤酒时,生产啤酒的总量与所需大麦芽吨数的关系。
教材第43页“自主练习”第2题
1
(1) 播音员播音的时间和字数如下表。
时间(分) 5 8 10 12 20
字数 1250 2000 2500 3000 5000
播音时间与播音字数成正比例吗?为什么?
250 250 250 250 250
=速度(一定)
播音时间与播音字数成正比例
教材第43页“自主练习”第2题
1
(2)播音员的已播字数和未播字数如下表。
时刻 8:02 8:03 8:04 8:05
已播字数 250 500 750 1000
未播字数 1250 1000 750 500
已播字数和未播字数成正比例吗?为什么?
0.2 0.5 1 2
的比值不一定
,已播字数和未播字数不成正比例
教材第43页“自主练习”第3题
2
说一说,生活中哪两种量成正比例关系?
单价一定,总价和数量成正比例。
圆柱的底面积一定,它的体积与高成正比例。
我知道了,圆锥的底面积一定,它的体积与高也成正比例。
教材第43页“自主练习”第4题
3
判断下面每题中的两种量是不是成正比例,并说明理由。
(1)天数一定,生产零件的总个数与每天生产零件的个数。
(一定),所以它们成正比例。
教材第43页“自主练习”第4题
3
判断下面每题中的两种量是不是成正比例,并说明理由。
(2)平行四边形的高一定,它的底与面积。
(一定)
平行四边形的高一定,它的底与面积成正比例。
平行四边形面积公式:S=ah
教材第43页“自主练习”第4题
3
判断下面每题中的两种量是不是成正比例,并说明理由。
(3)一个人的年龄与体重。
人的年龄与体重不成正比例,因为体重虽然随着年龄的变化而变化,但这种变化没有规律,即两种量的比值不固定,所以它们不成正比例。
教材第43页“自主练习”第4题
3
判断下面每题中的两种量是不是成正比例,并说明理由。
(4)正方形的边长与周长。
(一定)
正方形的边长与周长成正比例。
正方形的周长公式:C=4a
教材第44页“自主练习”第5题
4
已知x和y成正比例,请将下表填完整。
x 2 0.6 5
y 10 15 0.2
x和y成正比例,故
5
3
3
0.04
25
教材第44页“自主练习”第6题
5
一辆汽车行驶的路程与时间的关系如下图。
(1)从图中你发现了什么?
根据汽车行驶的路程与时间的关系所绘出的图像是一条经过原点的直线。汽车行驶的路程与时间成正比例关系。
教材第44页“自主练习”第6题
5
一辆汽车行驶的路程与时间的关系如下图。
(2)根据右图估计一下,要行驶600千米大约需要多少小时?
从图中来看,要行驶600千米大约需要7.5小时。
600
7.5
教材第44页“自主练习”第6题
5
一辆汽车行驶的路程与时间的关系如下图。
(3)估计一下这辆汽车8.5小时大约行驶多少千米。
从图中来看,这辆汽车8.5小时大约行驶680千米。
8.5
680
教材第45页“自主练习”第9题
6
在一定的弹性限度内,弹簧伸长的长度与所挂物体的质量情况如下表。
物体质量(kg) 0 1 2 3 4 5 6 7
弹簧伸长长度(cm) 0 0.5 1 1.5 2 2.5 3 3.5
2 2 2 2 2 2 2
的比值(一定)
这两个量之间成正比例
(1)弹簧伸长的长度与所挂物体的质量成正比例关系吗?说明理由。
教材第45页“自主练习”第9题
(2)在左图中描出表示物体质量和弹簧伸长长度相对应的点,然后把它们按顺序连接起来。
6
在一定的弹性限度内,弹簧伸长的长度与所挂物体的质量情况如下表。
物体质量(kg) 0 1 2 3 4 5 6 7
弹簧伸长长度(cm) 0 0.5 1 1.5 2 2.5 3 3.5
教材第45页“自主练习”第9题
(3)根据左图估计一下,称2.5千克物体时,弹簧大约伸长多少厘米?
从图表来看弹簧大约伸长1.25厘米。
6
在一定的弹性限度内,弹簧伸长的长度与所挂物体的质量情况如下表。
物体质量(kg) 0 1 2 3 4 5 6 7
弹簧伸长长度(cm) 0 0.5 1 1.5 2 2.5 3 3.5
2.5
1.25
同学们,这节课你有什么收获?
1.如果用字母x和y分别表示两种相关联的 量,用k表示它们的比值,若k值一定,那么x和y成正比例关系,这种关系可以用下面的式子表示:。
2.正比例关系图像是一条经过原点的直线。
课时练。
02
01
课后练习题。
正比例意义
青岛版数学六年级(下)
三 啤酒生产中的数学
——比 例
理解正比例的意义,能根据正比例的意义正确判断两种量是否成正比例。
认识正比例图像,能画出相应的正比例图像。
经历比较、分析、归纳等数学活动,提高分析比较和归纳概括能力,渗透函数思想。
【重点】
理解正比例的意义,会判断两种量是否成正比例。
【难点】
能画出相应的正比例图像,能根据
图像解决相关的实际问题。
0
0
1
15
2
30
3
45
4
60
5
90
6
75
7
105
……
……
工作时间
(时)
你能提出什么问题?
从图中你知道了哪些信息?
工作总量
(吨)
啤酒生产情况记录表
0
0
1
15
2
30
3
45
4
60
5
90
6
75
7
105
……
……
工作时间
(时)
啤酒生产情况记录表
工作总量
(吨)
工作总量和工作时间有什么关系呢
0
0
1
15
2
30
3
45
4
60
5
90
6
75
7
105
……
工作时间
(时)
工作总量
(吨)
……
观察记录表,发现规律
工作总量与工作时间是两种相关联的量,工作总量是随着工作时间的变化而变化的。
工作时间越长,生产的啤酒越多;工作时间越短,生产的啤酒越少。
,……工作总量与工作时间的比值一定。
工作总量和工作时间的变化情况可以用下图表示。
我发现根据工作总量和工作时间的关系所绘出的图像是一条直线。
工作总量和工作时间的比值就是工作效率。用式子表示它们的关系:
=工作效率(一定)
用数量关系式表示工作总量和工作时间的关系
正比例的意义
工作总量和工作时间是两种相关联的量,工作时间变化,工作总量也随着变化。工作效率不变,也就是工作总量与工作时间的比值一定,我们就说工作总量和工作时间是成正比例的量,它们的关系叫作正比例关系。
用字母表示正比例关系
如果用字母x和y分别表示两种相关联的量,用k表示它们的比值(一定),正比例关系可以用下面的式子表示:
试一试
教材第43页“自主练习”第1题
“神舟九号”飞船太空飞行情况记录如下。
时间(秒) 1 2 3 4 …… 10
路程(千米) 7.9 15.8 23.7 31.6 …… 79
表中的路程和时间成正比例吗?为什么?
7.9 7.9 7.9 7.9 …… 7.9
=速度(一定)
表中的路程和时间成正比例
以匀速行驶的汽车行驶的路程与行驶时间。
正方形的周长与它的边长。
圆的直径长度与它的半径长度。
想一想,生活中还有哪两种量成正比例关系?
下图是生产某种啤酒时,生产啤酒的总量与所需大麦芽吨数的关系。
横轴表示所需大麦芽的吨数,1个单位长度代表1吨
纵轴表示生产啤酒的总量,1个单位长度代表10吨
图像该怎么理解呢?
下图是生产某种啤酒时,生产啤酒的总量与所需大麦芽吨数的关系。
生产啤酒的总量对应的所需大麦芽的吨数都可以用图中的一个点表示,试一试。
1吨大麦芽生产10吨啤酒
可以用(1,10)表示
3吨大麦芽生产30吨啤酒
可以用(3,30)表示
下图是生产某种啤酒时,生产啤酒的总量与所需大麦芽吨数的关系。
(1)从图中你可以发现什么
①图像是一条经过原点的直线。
下图是生产某种啤酒时,生产啤酒的总量与所需大麦芽吨数的关系。
(1)从图中你可以发现什么
②生产啤酒总量和所需大麦芽吨数之间的变化规律:大麦芽的吨数越多,生产啤酒总量越多;大麦芽的吨数越少,生产啤酒总量越少。
下图是生产某种啤酒时,生产啤酒的总量与所需大麦芽吨数的关系。
(1)从图中你可以发现什么
③经过计算发现啤酒总量和大麦芽的吨数的比值一定,它们成正比例关系,这是一个正比例图像。正比例图像是一条通过原点的直线。
(2)根据此图说一说,用7吨大麦芽能生产多少吨啤酒
从图像中可以看出,用7吨大麦芽能生产70吨啤酒。
下图是生产某种啤酒时,生产啤酒的总量与所需大麦芽吨数的关系。
(3)估计一下,要生产95吨啤酒大约需要多少吨大麦芽
95
9.5
从图像中可以看出,要生产95吨啤酒大约需要9.5吨大芽。
下图是生产某种啤酒时,生产啤酒的总量与所需大麦芽吨数的关系。
教材第43页“自主练习”第2题
1
(1) 播音员播音的时间和字数如下表。
时间(分) 5 8 10 12 20
字数 1250 2000 2500 3000 5000
播音时间与播音字数成正比例吗?为什么?
250 250 250 250 250
=速度(一定)
播音时间与播音字数成正比例
教材第43页“自主练习”第2题
1
(2)播音员的已播字数和未播字数如下表。
时刻 8:02 8:03 8:04 8:05
已播字数 250 500 750 1000
未播字数 1250 1000 750 500
已播字数和未播字数成正比例吗?为什么?
0.2 0.5 1 2
的比值不一定
,已播字数和未播字数不成正比例
教材第43页“自主练习”第3题
2
说一说,生活中哪两种量成正比例关系?
单价一定,总价和数量成正比例。
圆柱的底面积一定,它的体积与高成正比例。
我知道了,圆锥的底面积一定,它的体积与高也成正比例。
教材第43页“自主练习”第4题
3
判断下面每题中的两种量是不是成正比例,并说明理由。
(1)天数一定,生产零件的总个数与每天生产零件的个数。
(一定),所以它们成正比例。
教材第43页“自主练习”第4题
3
判断下面每题中的两种量是不是成正比例,并说明理由。
(2)平行四边形的高一定,它的底与面积。
(一定)
平行四边形的高一定,它的底与面积成正比例。
平行四边形面积公式:S=ah
教材第43页“自主练习”第4题
3
判断下面每题中的两种量是不是成正比例,并说明理由。
(3)一个人的年龄与体重。
人的年龄与体重不成正比例,因为体重虽然随着年龄的变化而变化,但这种变化没有规律,即两种量的比值不固定,所以它们不成正比例。
教材第43页“自主练习”第4题
3
判断下面每题中的两种量是不是成正比例,并说明理由。
(4)正方形的边长与周长。
(一定)
正方形的边长与周长成正比例。
正方形的周长公式:C=4a
教材第44页“自主练习”第5题
4
已知x和y成正比例,请将下表填完整。
x 2 0.6 5
y 10 15 0.2
x和y成正比例,故
5
3
3
0.04
25
教材第44页“自主练习”第6题
5
一辆汽车行驶的路程与时间的关系如下图。
(1)从图中你发现了什么?
根据汽车行驶的路程与时间的关系所绘出的图像是一条经过原点的直线。汽车行驶的路程与时间成正比例关系。
教材第44页“自主练习”第6题
5
一辆汽车行驶的路程与时间的关系如下图。
(2)根据右图估计一下,要行驶600千米大约需要多少小时?
从图中来看,要行驶600千米大约需要7.5小时。
600
7.5
教材第44页“自主练习”第6题
5
一辆汽车行驶的路程与时间的关系如下图。
(3)估计一下这辆汽车8.5小时大约行驶多少千米。
从图中来看,这辆汽车8.5小时大约行驶680千米。
8.5
680
教材第45页“自主练习”第9题
6
在一定的弹性限度内,弹簧伸长的长度与所挂物体的质量情况如下表。
物体质量(kg) 0 1 2 3 4 5 6 7
弹簧伸长长度(cm) 0 0.5 1 1.5 2 2.5 3 3.5
2 2 2 2 2 2 2
的比值(一定)
这两个量之间成正比例
(1)弹簧伸长的长度与所挂物体的质量成正比例关系吗?说明理由。
教材第45页“自主练习”第9题
(2)在左图中描出表示物体质量和弹簧伸长长度相对应的点,然后把它们按顺序连接起来。
6
在一定的弹性限度内,弹簧伸长的长度与所挂物体的质量情况如下表。
物体质量(kg) 0 1 2 3 4 5 6 7
弹簧伸长长度(cm) 0 0.5 1 1.5 2 2.5 3 3.5
教材第45页“自主练习”第9题
(3)根据左图估计一下,称2.5千克物体时,弹簧大约伸长多少厘米?
从图表来看弹簧大约伸长1.25厘米。
6
在一定的弹性限度内,弹簧伸长的长度与所挂物体的质量情况如下表。
物体质量(kg) 0 1 2 3 4 5 6 7
弹簧伸长长度(cm) 0 0.5 1 1.5 2 2.5 3 3.5
2.5
1.25
同学们,这节课你有什么收获?
1.如果用字母x和y分别表示两种相关联的 量,用k表示它们的比值,若k值一定,那么x和y成正比例关系,这种关系可以用下面的式子表示:。
2.正比例关系图像是一条经过原点的直线。
课时练。
02
01
课后练习题。
