五奥运奖牌——扇形统计图 智慧广场(课件) 数学六年级下册青岛版(共15张PPT)
文档属性
| 名称 | 五奥运奖牌——扇形统计图 智慧广场(课件) 数学六年级下册青岛版(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-01 07:11:53 | ||
图片预览






文档简介
(共15张PPT)
智慧广场
青岛版数学六年级(下)
五 奥运奖牌
——扇形统计图
借助生活情境,了解“鸡兔同笼”问题,在运用一一列举法解决问题的过程中,发现规律并学会运用假设的策略解决问题。
熟练运用假设的方法建立数学模型,培养数学建模能力和逻辑推理能力。
【重点】
运用假设的方法建立数学模型。
【难点】
正确建立数学模型并求解。
你能解决这个问题吗
一个停车场里停有四轮小汽车和两轮摩托车共24辆。如果这些车共有86个轮子,那么停车场里有几辆小汽车和几辆摩托车
我用列举的方法。
小汽车数 摩托车数 轮子数
24 0 4×24=96
23 1 4×23+2×1=94
22 2 4×22+2×2=92
21 3 4×21+2×3=90
…… …… ……
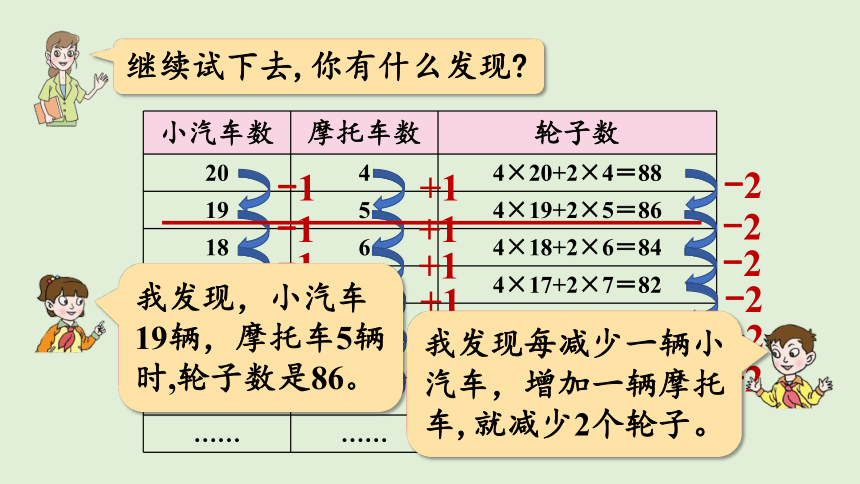
继续试下去,你有什么发现
小汽车数 摩托车数 轮子数
20 4 4×20+2×4=88
19 5 4×19+2×5=86
18 6 4×18+2×6=84
17 7 4×17+2×7=82
16 8 4×16+2×8=80
15 9 4×15+2×9=78
14 10 4×14+2×10=76
…… …… ……
-1
+1
-2
-1
+1
-2
-1
+1
-2
-1
+1
-2
-1
+1
-2
-1
+1
-2
我发现,小汽车19辆,摩托车5辆时,轮子数是86。
我发现每减少一辆小汽车,增加一辆摩托车,就减少2个轮子。
我会用算式表达。
(4×24-86)÷(4-2) =5(辆)
24-5=19(辆)
当小汽车数是24,摩托车数为0时,轮子总数:4×24=96
比实际多出的轮子数:96-86=10
一辆小汽车比一辆摩托车多的轮子数:4-2=2
摩托车数:10÷2=5
小汽车数:24-5=19
想一想,这个问题还可以怎样解决
我用列方程的方法求解。
解:设停车场有小汽车x辆。
则有摩托车(24-x)辆
4×x+ (24-x)×2= 86
4x-2x=86-48
2x=38
x=19
24-x=24-19=5
答:停车场有小汽车19辆,摩托车5辆。
小汽车轮子数
摩托车轮子数
轮子总数
1
教材第82页“自主练习”第1题
一只蛐蛐6条腿,一只蜘蛛8条腿。现有蛐蛐和蜘蛛共10只,共有68条腿。蛐蛐和蜘蛛各有几只
1
假设蜘蛛的数量是10只,蛐蛐的数量是0只,那么腿的总数:8×10=80(条)
比实际多出的腿的数量:80-68=12(条)
一只蜘蛛比一只蛐蛐多的腿数:8-6=2(条)
蛐蛐数量:12÷2=6(只)
蜘蛛数量:10-6=4(只)
答:蛐蛐有6只,蜘蛛有4只。
教材第82页“自主练习”第2题
王丽有20张5元和2元的人民币,面值一共是82元。5元和2元的人民币各有多少张
2
假设5元的数量是20张,2元的数量是0张,那么总面值是:
5×20=100
比实际多出的面值:
100-82=18
5元比2元面值大:5-2=3
2元纸币的数量:18÷3=6
5元纸币的数量:20-6=14
(5×20-82)÷(5-2) =6(张)
20-6=14(张)
答: 5元和2元纸币的数量分别为14张和6张。
教材第82页“自主练习”第3题
学校买来50张电影票,一部分是4元一张的学生票,一部分是6元一张的成人票,总票价是260元。两种票各买了多少张
3
(6×50-260) ÷ (6-4) = 20 (张)
50–20 = 30(张)
答: 6元和4元的票分别购买了30张和20张。
假设50张电影票全是6元的
比实际票价多出的价格
6元票价比4元票价多多少
一个房间里有4条腿的椅子和3条腿的凳子共18个。如果椅子腿和凳子腿加起来共有68条,那么有几个椅子和几个凳子
4
教材第82页“自主练习”第4题
(4×18-68) ÷ (4-3) = 4 (个)
18–4 = 14(个)
假设椅子有18个
腿比实际多出的数量
椅子比凳子多的腿
答: 有14个椅子,4个凳子。
“今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何 ”这是我国古代数学著作《孙子算经》中的一道题目,把它翻译成现代汉语是:现在有一些鸡和兔子被关在同一个笼子里,鸡和兔共35个头、94只脚。问:鸡和兔各有多少只
5
教材第82页“自主练习”第5题
(4×35-94) ÷ (4-2) = 23 (只)
35–23 = 12(只)
假设兔子有35只
腿比实际多出的数量
兔子比鸡多的腿
答: 鸡有23只,兔子有12只。
假设法的含义:假设法就是根据题目中的已知条件或结论作出某种设想,然后进行推算,如果所得的结果与题意矛盾,再适当调整,以求得正确答案。
“鸡兔同笼”是典型的运用“假设法”解题的问题之一,其问题的基本关系式是:
兔数=(总脚数-每只鸡脚数×鸡兔总数)÷(每只兔子脚数-每只鸡脚数)
鸡数=鸡兔总数-兔数
作业课件中的相关练习。
02
01
课后练习题。
智慧广场
青岛版数学六年级(下)
五 奥运奖牌
——扇形统计图
借助生活情境,了解“鸡兔同笼”问题,在运用一一列举法解决问题的过程中,发现规律并学会运用假设的策略解决问题。
熟练运用假设的方法建立数学模型,培养数学建模能力和逻辑推理能力。
【重点】
运用假设的方法建立数学模型。
【难点】
正确建立数学模型并求解。
你能解决这个问题吗
一个停车场里停有四轮小汽车和两轮摩托车共24辆。如果这些车共有86个轮子,那么停车场里有几辆小汽车和几辆摩托车
我用列举的方法。
小汽车数 摩托车数 轮子数
24 0 4×24=96
23 1 4×23+2×1=94
22 2 4×22+2×2=92
21 3 4×21+2×3=90
…… …… ……
继续试下去,你有什么发现
小汽车数 摩托车数 轮子数
20 4 4×20+2×4=88
19 5 4×19+2×5=86
18 6 4×18+2×6=84
17 7 4×17+2×7=82
16 8 4×16+2×8=80
15 9 4×15+2×9=78
14 10 4×14+2×10=76
…… …… ……
-1
+1
-2
-1
+1
-2
-1
+1
-2
-1
+1
-2
-1
+1
-2
-1
+1
-2
我发现,小汽车19辆,摩托车5辆时,轮子数是86。
我发现每减少一辆小汽车,增加一辆摩托车,就减少2个轮子。
我会用算式表达。
(4×24-86)÷(4-2) =5(辆)
24-5=19(辆)
当小汽车数是24,摩托车数为0时,轮子总数:4×24=96
比实际多出的轮子数:96-86=10
一辆小汽车比一辆摩托车多的轮子数:4-2=2
摩托车数:10÷2=5
小汽车数:24-5=19
想一想,这个问题还可以怎样解决
我用列方程的方法求解。
解:设停车场有小汽车x辆。
则有摩托车(24-x)辆
4×x+ (24-x)×2= 86
4x-2x=86-48
2x=38
x=19
24-x=24-19=5
答:停车场有小汽车19辆,摩托车5辆。
小汽车轮子数
摩托车轮子数
轮子总数
1
教材第82页“自主练习”第1题
一只蛐蛐6条腿,一只蜘蛛8条腿。现有蛐蛐和蜘蛛共10只,共有68条腿。蛐蛐和蜘蛛各有几只
1
假设蜘蛛的数量是10只,蛐蛐的数量是0只,那么腿的总数:8×10=80(条)
比实际多出的腿的数量:80-68=12(条)
一只蜘蛛比一只蛐蛐多的腿数:8-6=2(条)
蛐蛐数量:12÷2=6(只)
蜘蛛数量:10-6=4(只)
答:蛐蛐有6只,蜘蛛有4只。
教材第82页“自主练习”第2题
王丽有20张5元和2元的人民币,面值一共是82元。5元和2元的人民币各有多少张
2
假设5元的数量是20张,2元的数量是0张,那么总面值是:
5×20=100
比实际多出的面值:
100-82=18
5元比2元面值大:5-2=3
2元纸币的数量:18÷3=6
5元纸币的数量:20-6=14
(5×20-82)÷(5-2) =6(张)
20-6=14(张)
答: 5元和2元纸币的数量分别为14张和6张。
教材第82页“自主练习”第3题
学校买来50张电影票,一部分是4元一张的学生票,一部分是6元一张的成人票,总票价是260元。两种票各买了多少张
3
(6×50-260) ÷ (6-4) = 20 (张)
50–20 = 30(张)
答: 6元和4元的票分别购买了30张和20张。
假设50张电影票全是6元的
比实际票价多出的价格
6元票价比4元票价多多少
一个房间里有4条腿的椅子和3条腿的凳子共18个。如果椅子腿和凳子腿加起来共有68条,那么有几个椅子和几个凳子
4
教材第82页“自主练习”第4题
(4×18-68) ÷ (4-3) = 4 (个)
18–4 = 14(个)
假设椅子有18个
腿比实际多出的数量
椅子比凳子多的腿
答: 有14个椅子,4个凳子。
“今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何 ”这是我国古代数学著作《孙子算经》中的一道题目,把它翻译成现代汉语是:现在有一些鸡和兔子被关在同一个笼子里,鸡和兔共35个头、94只脚。问:鸡和兔各有多少只
5
教材第82页“自主练习”第5题
(4×35-94) ÷ (4-2) = 23 (只)
35–23 = 12(只)
假设兔子有35只
腿比实际多出的数量
兔子比鸡多的腿
答: 鸡有23只,兔子有12只。
假设法的含义:假设法就是根据题目中的已知条件或结论作出某种设想,然后进行推算,如果所得的结果与题意矛盾,再适当调整,以求得正确答案。
“鸡兔同笼”是典型的运用“假设法”解题的问题之一,其问题的基本关系式是:
兔数=(总脚数-每只鸡脚数×鸡兔总数)÷(每只兔子脚数-每只鸡脚数)
鸡数=鸡兔总数-兔数
作业课件中的相关练习。
02
01
课后练习题。
