信息窗3 圆柱和圆锥的体积第1课时-圆柱体积(课件) 数学六年级下册青岛版(共24张PPT)
文档属性
| 名称 | 信息窗3 圆柱和圆锥的体积第1课时-圆柱体积(课件) 数学六年级下册青岛版(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-01 07:13:41 | ||
图片预览





文档简介
(共24张PPT)
圆柱体积
青岛版数学六年级(下)
二 冰淇淋盒有多大
——圆柱和圆锥
理解并掌握圆柱体积的计算方法,并能解决简单的实际问题。
熟悉圆柱体积计算公式的推导过程,建立起一定的空间观念。
学习目标
掌握圆柱体积的计算方法,以及圆柱体体积公式的探索推导过程。
理解并掌握圆柱体积公式的简单计算。
【难点】
【重点】
课堂导入
12cm
20cm
3
左边这个圆柱形包装盒的高和底面直径是已知的,那么你还能提出什么问题呢?
新知探究
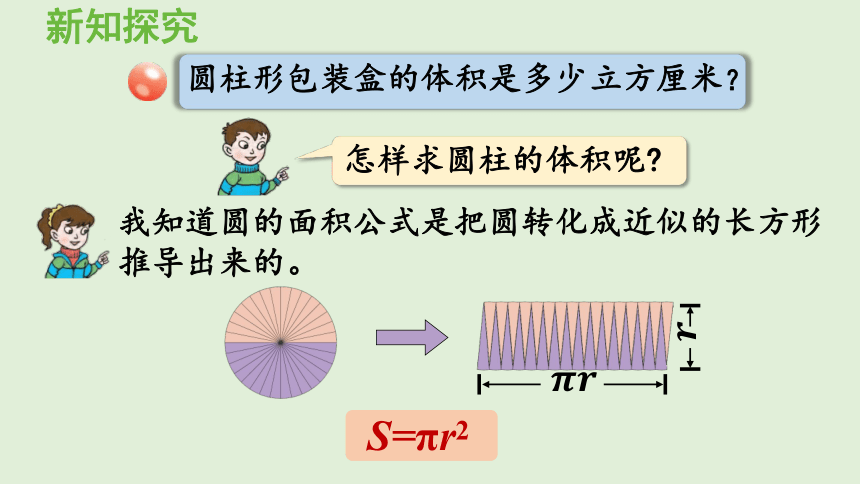
圆柱形包装盒的体积是多少立方厘米?
怎样求圆柱的体积呢
我知道圆的面积公式是把圆转化成近似的长方形推导出来的。
S=πr2
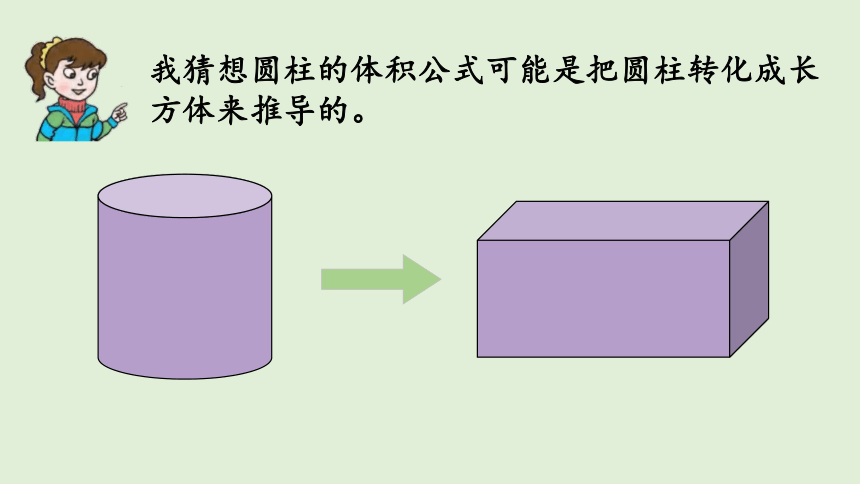
我猜想圆柱的体积公式可能是把圆柱转化成长方体来推导的。
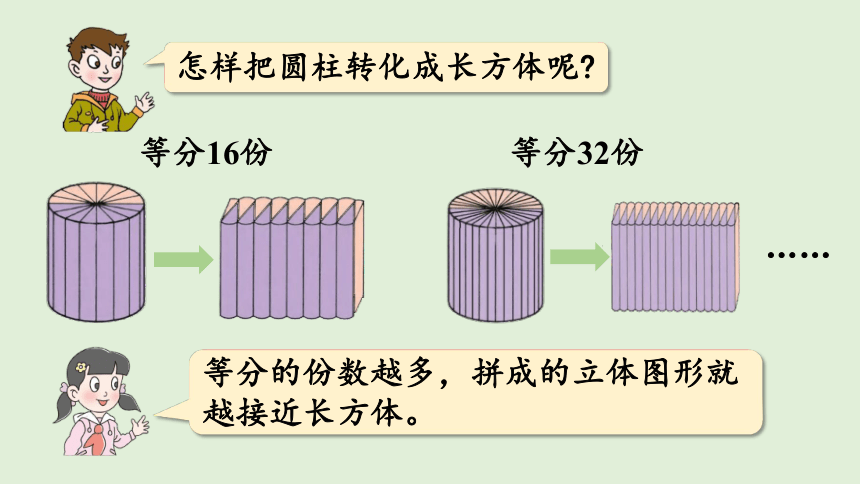
等分16份
等分32份
怎样把圆柱转化成长方体呢
等分的份数越多,拼成的立体图形就越接近长方体。
……
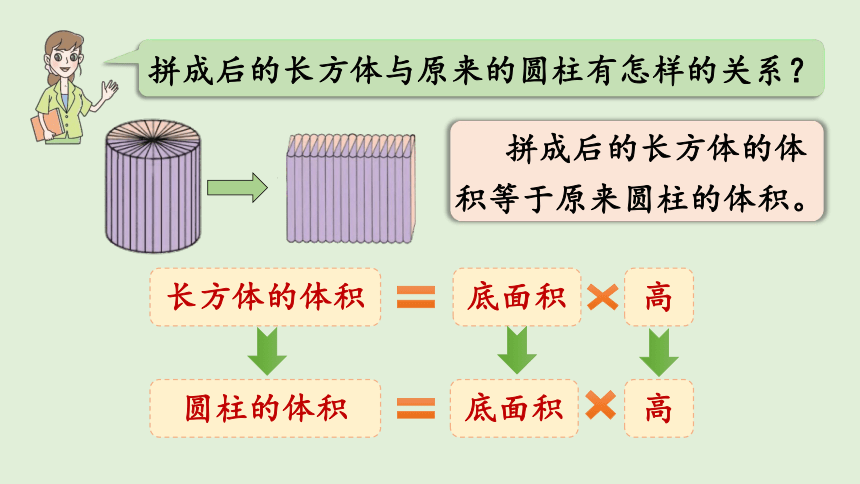
拼成后的长方体的体积等于原来圆柱的体积。
长方体的体积
底面积
高
圆柱的体积
底面积
高
拼成后的长方体与原来的圆柱有怎样的关系?
圆柱的体积=底面积×高
V=Sh
底面积:
3.14×(12÷2)2=113.04 (cm2)
体 积:
113.04×20=2260.8 (cm3)
答:圆柱形包装盒的体积是2260.8cm3。
12cm
20cm
课堂练习
底 面 积(S):
体 积(V):
3.14×32
=28.26(平方厘米)
28.26×10
=282.6(立方厘米)
底面半径(r):
3厘米
高 (h):
10厘米
1
计算下列图形的体积。
(单位:厘米)
圆柱的体积=底面积×高
V=Sh
10
3
(教材第27页“自主练习”第1题)
8
8
底 面 积(S):
体 积(V):
3.14×42
=50.24(平方厘米)
50.24×8
=401.92(立方厘米)
底面半径(r):
=4(厘米)
高 (h):
8厘米
8÷2
10
4
底 面 积(S):
体 积(V):
3.14×22
=12.56(平方厘米)
12.56×10
=125.6(立方厘米)
底面半径(r):
=2(厘米)
高 (h):
10厘米
4÷2
2
哪一根木料的体积大?
底面积(S):
体 积(V):
3.14×0.22
=0.1256(m2)
0.1256×10
=1.256(m3)
半 径(r):
=0.2(m)
高 (h):
10m
0.4÷2
底面积(S):
体 积(V):
3.14×0.32
=0.2826(m2)
0.2826×8
=2.2608(m3)
半 径(r):
=0.3(m)
高 (h):
8m
0.6÷2
<
答:右侧木料的体积大。
(教材第27页“自主练习”第2题)
分析:
一只水杯,从里面量底面直径是8厘米,高10厘米。
一桶纯净水大约可以倒满多少杯呢
水杯里面是圆柱形的,要知道一桶水可以倒满多少杯,只需要知道水桶的容积是水杯容积的多少倍,已知水桶的容积是19升,也就是要计算出水杯的容积,再用水桶的容积除以水杯的容积。
3
净含量:
19升
(教材第27页“自主练习”第4题)
水杯底面积(S):
水杯容积 (V):
3.14×42
=50.24(cm2)
50.24×10
=502.4(cm3)
水杯半径 (r):
=4(cm)
水杯的高 (h):
10cm
8÷2
1cm3=1mL=0.001L
=0.5024L
19÷0.5024
≈38(杯)
答:一桶纯净水大约可以倒满38杯。
解答
油桶底面积(S):
油桶容积 (V):
3.14×202
=1256(平方厘米)
1256×50
=62800(立方厘米)
油桶半径 (r):
=20(厘米)
油桶的高 (h):
50厘米
40÷2
=62.8(升)
答:它的容积是62.8升。
4
一个圆柱形油桶,从里面量底面直径是40厘米,高是50厘米。
(1)它的容积是多少升
(2)如果1升柴油重0.85千克,这个油桶可装多少千克柴油
62.8÷0.85
≈73.88(千克)
答:这个油桶可装73.88千克柴油。
(教材第28页“自主练习”第5题)
5
计算下列图形的表面积和体积。
表面积计算公式:
S=2×(10×6+6×4+4×10)
= 2×124
= 248 (cm2)
体积计算公式:
V= 10×6×4 = 240 (cm3)
(教材第29页“自主练习”第10题)
表面积计算公式:
体积计算公式:
V= 3.14×(4÷2)2×6
= 12.56×6
= 75.36 (cm3)
侧面积:
底面积:
表面积:
3.14×4×6
=75.36(cm2)
3.14×(4÷2)2
=12.56(cm2)
75.36+12.56×2
=100.48(cm2)
表面积计算公式:
S= 6×52
= 6×25
= 150(dm2)
体积计算公式:
V=53
= 5×5×5
= 125 (dm3)
分析:
一棵巨杉高达140米。它的树干上下几乎一样粗,横截面周长是37.68米。你能提出什么问题?
6
3.14×(37.68÷3.14÷2)2×140
= 3.14×36×140
= 15825.6 (m3)
提问:这棵树的体积是多少?
由题意可知,这棵树近似一个圆柱体,要知道这棵树的体积,可以按圆柱的体积计算公式进行计算。
答:这棵树的体积是15825.6 m3 。
(教材第29页“自主练习”第11题)
一张铁皮长62.8厘米,宽31.4厘米。张师傅想用这张铁皮做侧面(接头处忽略不计),加工成一个无盖的圆柱形小桶,可以配制多大面积的底面 哪种方法加工成的小桶容积大 (可用计算器计算)
7
制作方法一
制作方法二
31.4cm
62.8cm
62.8cm
31.4cm
(教材第29页“自主练习”第13题)
底面周长:62.8厘米
高:31.4厘米
底 面 积(S):
容 积(V):
3.14×102
=314(cm2)
314×31.4
=9859.6(cm3)
底面半径(r):
=10(cm)
高 (h):
31.4cm
62.8÷3.14÷2
按此种制作方法,需配制314平方厘米的底面。
方法一
方法二
底面周长:31.4厘米
高:62.8厘米
底 面 积(S):
容 积(V):
3.14×52
=78.5(cm2)
78.5×62.8
=4929.8(cm3)
底面半径(r):
=5(cm)
高 (h):
62.8cm
31.4÷3.14÷2
按此种制作方法,需配制78.5平方厘米的底面。且这种方法制作的小桶容积最大。
课堂小结
圆柱的体积是怎么计算的呢,你能写出圆柱的体积计算公式吗?
要计算一个圆柱的体积,只要用它的底面面积乘以它的高就可以了。
圆柱的体积计算公式是:
圆柱的体积=底面积×高
V=Sh
课后作业
作业课件中的相关练习。
圆柱体积
青岛版数学六年级(下)
二 冰淇淋盒有多大
——圆柱和圆锥
理解并掌握圆柱体积的计算方法,并能解决简单的实际问题。
熟悉圆柱体积计算公式的推导过程,建立起一定的空间观念。
学习目标
掌握圆柱体积的计算方法,以及圆柱体体积公式的探索推导过程。
理解并掌握圆柱体积公式的简单计算。
【难点】
【重点】
课堂导入
12cm
20cm
3
左边这个圆柱形包装盒的高和底面直径是已知的,那么你还能提出什么问题呢?
新知探究
圆柱形包装盒的体积是多少立方厘米?
怎样求圆柱的体积呢
我知道圆的面积公式是把圆转化成近似的长方形推导出来的。
S=πr2
我猜想圆柱的体积公式可能是把圆柱转化成长方体来推导的。
等分16份
等分32份
怎样把圆柱转化成长方体呢
等分的份数越多,拼成的立体图形就越接近长方体。
……
拼成后的长方体的体积等于原来圆柱的体积。
长方体的体积
底面积
高
圆柱的体积
底面积
高
拼成后的长方体与原来的圆柱有怎样的关系?
圆柱的体积=底面积×高
V=Sh
底面积:
3.14×(12÷2)2=113.04 (cm2)
体 积:
113.04×20=2260.8 (cm3)
答:圆柱形包装盒的体积是2260.8cm3。
12cm
20cm
课堂练习
底 面 积(S):
体 积(V):
3.14×32
=28.26(平方厘米)
28.26×10
=282.6(立方厘米)
底面半径(r):
3厘米
高 (h):
10厘米
1
计算下列图形的体积。
(单位:厘米)
圆柱的体积=底面积×高
V=Sh
10
3
(教材第27页“自主练习”第1题)
8
8
底 面 积(S):
体 积(V):
3.14×42
=50.24(平方厘米)
50.24×8
=401.92(立方厘米)
底面半径(r):
=4(厘米)
高 (h):
8厘米
8÷2
10
4
底 面 积(S):
体 积(V):
3.14×22
=12.56(平方厘米)
12.56×10
=125.6(立方厘米)
底面半径(r):
=2(厘米)
高 (h):
10厘米
4÷2
2
哪一根木料的体积大?
底面积(S):
体 积(V):
3.14×0.22
=0.1256(m2)
0.1256×10
=1.256(m3)
半 径(r):
=0.2(m)
高 (h):
10m
0.4÷2
底面积(S):
体 积(V):
3.14×0.32
=0.2826(m2)
0.2826×8
=2.2608(m3)
半 径(r):
=0.3(m)
高 (h):
8m
0.6÷2
<
答:右侧木料的体积大。
(教材第27页“自主练习”第2题)
分析:
一只水杯,从里面量底面直径是8厘米,高10厘米。
一桶纯净水大约可以倒满多少杯呢
水杯里面是圆柱形的,要知道一桶水可以倒满多少杯,只需要知道水桶的容积是水杯容积的多少倍,已知水桶的容积是19升,也就是要计算出水杯的容积,再用水桶的容积除以水杯的容积。
3
净含量:
19升
(教材第27页“自主练习”第4题)
水杯底面积(S):
水杯容积 (V):
3.14×42
=50.24(cm2)
50.24×10
=502.4(cm3)
水杯半径 (r):
=4(cm)
水杯的高 (h):
10cm
8÷2
1cm3=1mL=0.001L
=0.5024L
19÷0.5024
≈38(杯)
答:一桶纯净水大约可以倒满38杯。
解答
油桶底面积(S):
油桶容积 (V):
3.14×202
=1256(平方厘米)
1256×50
=62800(立方厘米)
油桶半径 (r):
=20(厘米)
油桶的高 (h):
50厘米
40÷2
=62.8(升)
答:它的容积是62.8升。
4
一个圆柱形油桶,从里面量底面直径是40厘米,高是50厘米。
(1)它的容积是多少升
(2)如果1升柴油重0.85千克,这个油桶可装多少千克柴油
62.8÷0.85
≈73.88(千克)
答:这个油桶可装73.88千克柴油。
(教材第28页“自主练习”第5题)
5
计算下列图形的表面积和体积。
表面积计算公式:
S=2×(10×6+6×4+4×10)
= 2×124
= 248 (cm2)
体积计算公式:
V= 10×6×4 = 240 (cm3)
(教材第29页“自主练习”第10题)
表面积计算公式:
体积计算公式:
V= 3.14×(4÷2)2×6
= 12.56×6
= 75.36 (cm3)
侧面积:
底面积:
表面积:
3.14×4×6
=75.36(cm2)
3.14×(4÷2)2
=12.56(cm2)
75.36+12.56×2
=100.48(cm2)
表面积计算公式:
S= 6×52
= 6×25
= 150(dm2)
体积计算公式:
V=53
= 5×5×5
= 125 (dm3)
分析:
一棵巨杉高达140米。它的树干上下几乎一样粗,横截面周长是37.68米。你能提出什么问题?
6
3.14×(37.68÷3.14÷2)2×140
= 3.14×36×140
= 15825.6 (m3)
提问:这棵树的体积是多少?
由题意可知,这棵树近似一个圆柱体,要知道这棵树的体积,可以按圆柱的体积计算公式进行计算。
答:这棵树的体积是15825.6 m3 。
(教材第29页“自主练习”第11题)
一张铁皮长62.8厘米,宽31.4厘米。张师傅想用这张铁皮做侧面(接头处忽略不计),加工成一个无盖的圆柱形小桶,可以配制多大面积的底面 哪种方法加工成的小桶容积大 (可用计算器计算)
7
制作方法一
制作方法二
31.4cm
62.8cm
62.8cm
31.4cm
(教材第29页“自主练习”第13题)
底面周长:62.8厘米
高:31.4厘米
底 面 积(S):
容 积(V):
3.14×102
=314(cm2)
314×31.4
=9859.6(cm3)
底面半径(r):
=10(cm)
高 (h):
31.4cm
62.8÷3.14÷2
按此种制作方法,需配制314平方厘米的底面。
方法一
方法二
底面周长:31.4厘米
高:62.8厘米
底 面 积(S):
容 积(V):
3.14×52
=78.5(cm2)
78.5×62.8
=4929.8(cm3)
底面半径(r):
=5(cm)
高 (h):
62.8cm
31.4÷3.14÷2
按此种制作方法,需配制78.5平方厘米的底面。且这种方法制作的小桶容积最大。
课堂小结
圆柱的体积是怎么计算的呢,你能写出圆柱的体积计算公式吗?
要计算一个圆柱的体积,只要用它的底面面积乘以它的高就可以了。
圆柱的体积计算公式是:
圆柱的体积=底面积×高
V=Sh
课后作业
作业课件中的相关练习。
