总复习—二图形与几何 第3课时 立体图形的认识与测量(课件) 数学 六年级下册青岛版(共44张PPT)
文档属性
| 名称 | 总复习—二图形与几何 第3课时 立体图形的认识与测量(课件) 数学 六年级下册青岛版(共44张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-01 00:00:00 | ||
图片预览



文档简介
(共44张PPT)
第3课时 立体图形的认识与测量
青岛版数学六年级(下)
二 图形与几何
1.图形的认识与测量
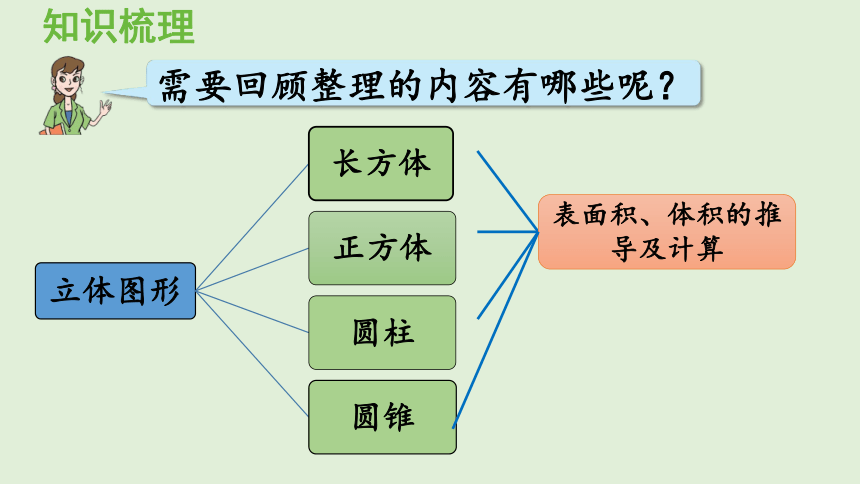
知识梳理
需要回顾整理的内容有哪些呢?
表面积、体积的推导及计算
要点回顾
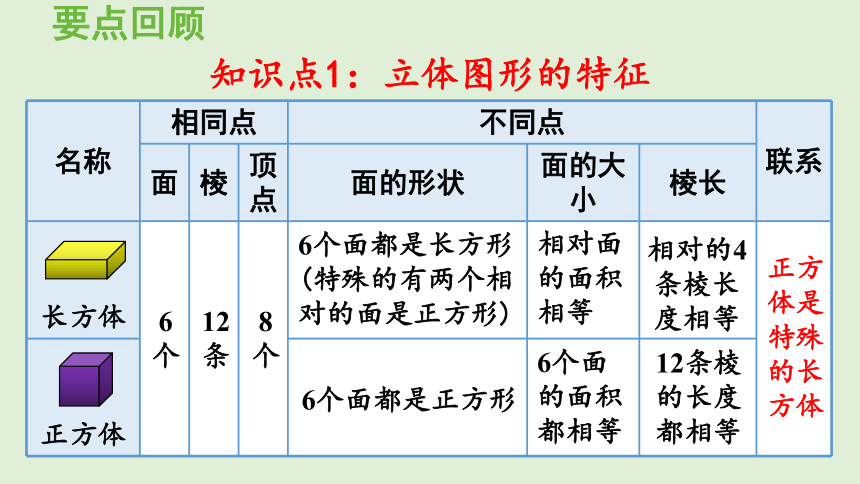
知识点1:立体图形的特征
名称 相同点 不同点 联系
面 棱 顶点 面的形状 面的大小 棱长 长方体
正方体
6个
12条
8个
6个面都是长方形(特殊的有两个相对的面是正方形)
6个面都是正方形
相对面的面积相等
6个面的面积都相等
相对的4条棱长度相等
12条棱的长度都相等
正方体是特殊的长方体
名称 特征
圆柱
圆锥
有3个面:上、下底面是相等的两个圆,侧面是曲面。
有2个面:底面是圆,侧面是曲面。
两个底面之间的距离叫做高,有无数条长度相等的高。
顶点到底面圆心的距离叫做高,只有一条高。
侧面沿高剪开,展开后是长方形(正方形)。
侧面展开后可以得到一个扇形。
由长方形(正方形)的一边为轴旋转一周可以形成。
由直角三角形的一条直角边为轴旋转一周可以形成。
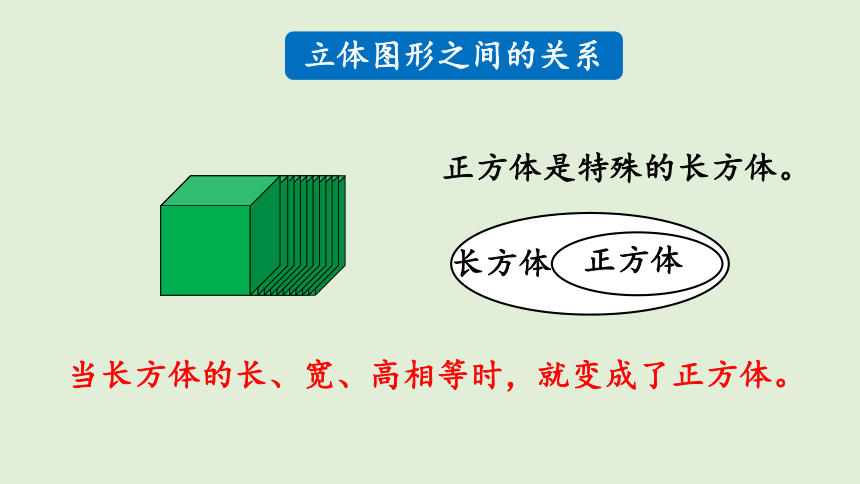
当长方体的长、宽、高相等时,就变成了正方体。
正方体是特殊的长方体。
长方体
正方体
立体图形之间的关系
当圆柱的上底面的面积等于 0 时,就变成了圆锥。
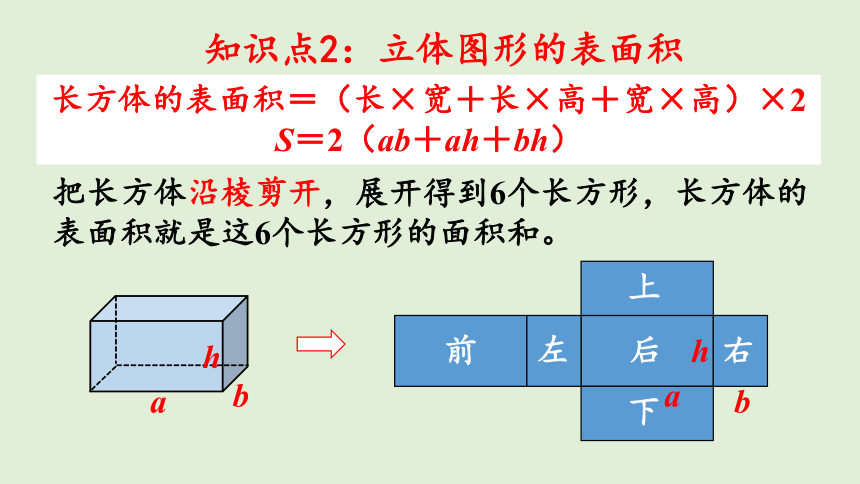
知识点2:立体图形的表面积
把长方体沿棱剪开,展开得到6个长方形,长方体的表面积就是这6个长方形的面积和。
长方体的表面积=(长×宽+长×高+宽×高)×2
S=2(ab+ah+bh)
a
b
h
a
b
h
前
后
左
右
上
下
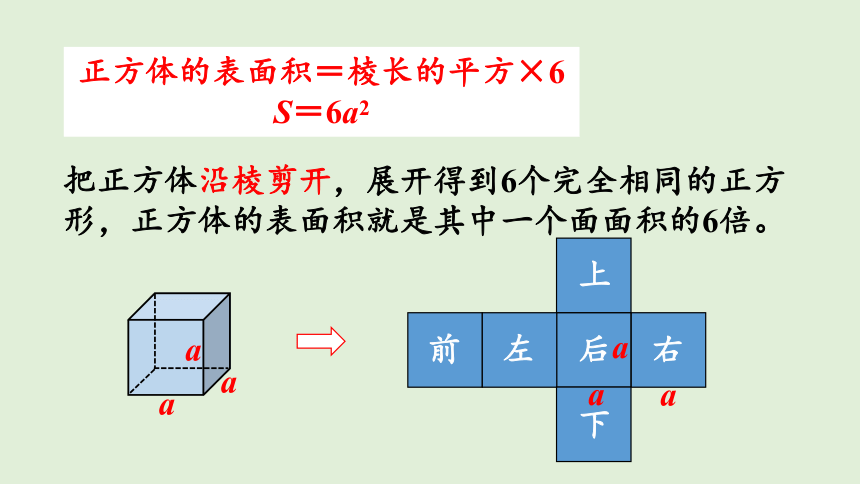
把正方体沿棱剪开,展开得到6个完全相同的正方形,正方体的表面积就是其中一个面面积的6倍。
正方体的表面积=棱长的平方×6
S=6a2
a
a
a
a
前
后
左
右
上
下
a
a
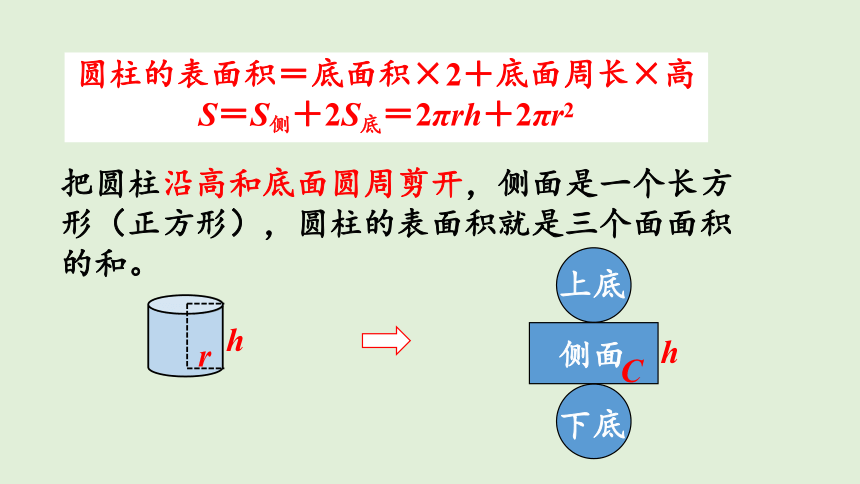
把圆柱沿高和底面圆周剪开,侧面是一个长方形(正方形),圆柱的表面积就是三个面面积的和。
圆柱的表面积=底面积×2+底面周长×高
S=S侧+2S底=2πrh+2πr2
r
h
C
侧面
上底
下底
h
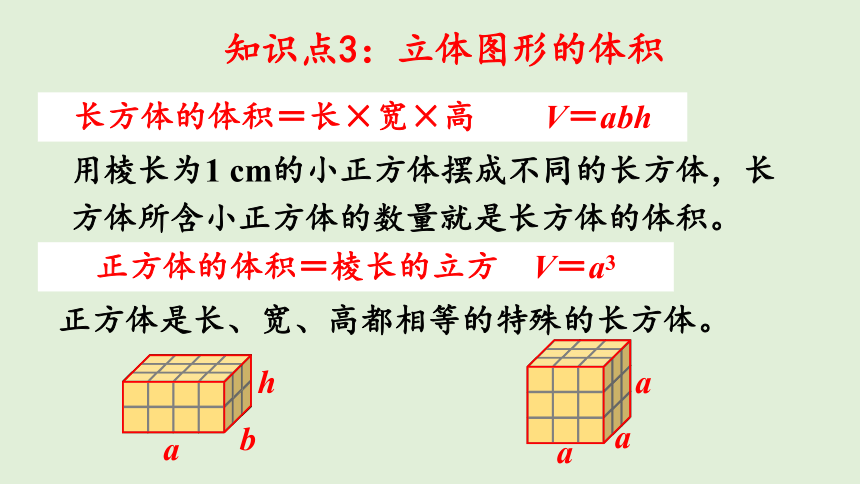
知识点3:立体图形的体积
用棱长为1 cm的小正方体摆成不同的长方体,长方体所含小正方体的数量就是长方体的体积。
长方体的体积=长×宽×高 V=abh
a
b
h
正方体是长、宽、高都相等的特殊的长方体。
正方体的体积=棱长的立方 V=a3
a
a
a
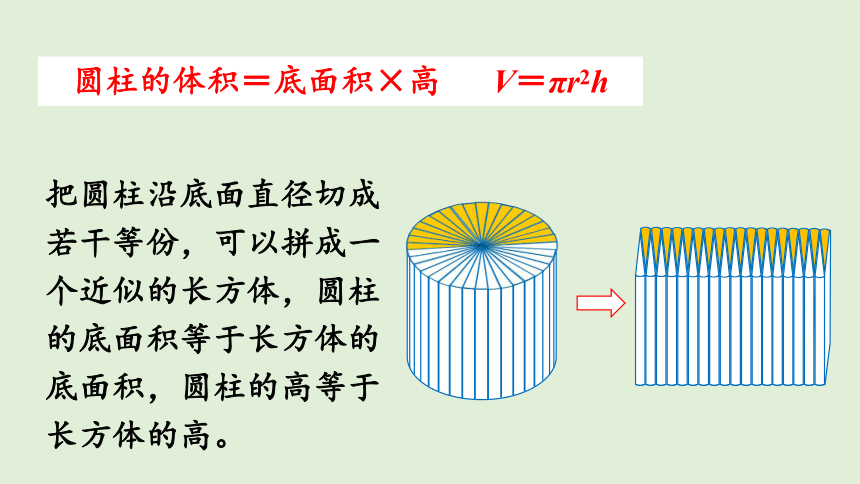
把圆柱沿底面直径切成若干等份,可以拼成一个近似的长方体,圆柱的底面积等于长方体的底面积,圆柱的高等于长方体的高。
圆柱的体积=底面积×高 V=πr2h
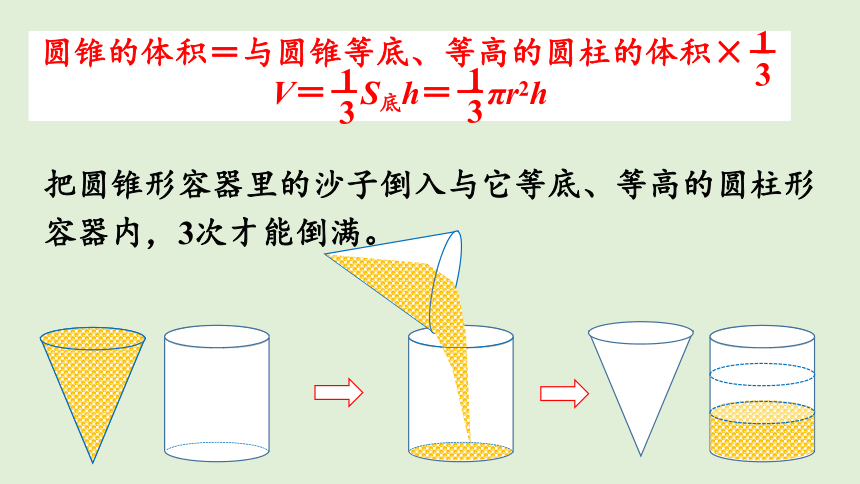
把圆锥形容器里的沙子倒入与它等底、等高的圆柱形容器内,3次才能倒满。
圆锥的体积=与圆锥等底、等高的圆柱的体积×-
V=-S底h=-πr2h
13
13
13
a
b
h
a
a
a
h
h
S
S
V=
ɑbh
V=
ɑ·ɑ·ɑ=ɑ
V =
Sh
V=
Sh
V = Sh
S
h
S
这些体积计算公式之间有怎样的联系呢?
知识点4:立体图形的应用
62.8cm
31.4cm
20cm
10cm
15.7cm
7.85cm
选择上面的材料制作一个水桶,有几种方案
联系已有知识经验想象水桶的形状
水桶的形状可能是长方体的,也可能是圆柱体的。
长方体水桶的侧面展开图是长方形,底面是正方形。
圆柱体水桶的侧面展开图是长方形,底面是圆形。
应选择长方形和正方形材料制作这样的水桶。
长方形的长或宽等于底面的周长。
选择长方形和圆形材料制作这个水桶。
长方形的长或宽等于底面的周长。
正方形边长:62.8÷4=15.7(厘米)
62.8cm的边作为底面周长。
可以选择长62.8cm、宽31.4cm的长方形做水桶侧面,边长为15.7cm的正方形做水桶的底。
制作长方体水桶
正方形边长:31.4÷4=7.85(厘米)
31.4cm的边作为底面周长。
可以选择长62.8cm、宽31.4cm的长方形做水桶侧面,边长为7.85cm的正方形做水桶的底。
底面直径:62.8÷3.14=20(厘米)
62.8cm的边作为底面周长。
可以选择长62.8cm、宽31.4cm的长方形做水桶侧面,底面直径为20cm的圆做水桶的底。
制作圆柱体水桶
底面直径:31.4÷3.14=10(厘米)
31.4cm的边作为底面周长。
可以选择长62.8cm、宽31.4cm的长方形做水桶侧面,底面直径为10cm的圆做水桶的底。
10cm
问题:怎样选择材料制作水桶
联系已有知识经验想象水桶的形状
水桶的侧面展开图是长方形
水桶的底面是圆形(或正方形)
选择长方形和圆形(或正方形)材料
长方形的长或宽等于底面的周长
形成制作水桶的方案
平面
立体
立体
总结一下这个问题的解决过程吧!
课堂练习
教材第105页“应用与反思”第14题
1. 我说你搭。
现在,请你在两个圆柱形积木的上面搭一块与底座的长和宽都相等的长方体积木.....
我从长方体积木中找,长和宽.....
小阳
小刚
教材第105页“应用与反思”第14题
(1)小阳应该怎样准确地描述呢
先要说清楚积木的形状和大小,再说清楚它的位置。
(2)小刚是怎样找到他需要的积木并确定它的位置的
先根据描述想象出符合要求的图形,找到相应的积木,再搭建要求的形状。
教材第106页“应用与反思”第16题
2.如果从正面和上面看到的都是右面的图形,你知道小正方体是怎样摆放的吗 摆摆看。
教材第106页“应用与反思”第17题
3.用铁皮做60个长为50厘米、底面半径为3厘米的圆柱形通风管。如果每平方米铁皮30元,做这些通风管需花多少钱
2×3.14×3×50×60=56520(平方厘米)
答:需要花169.56元。
56520平方厘米=5.652平方米
30×5.652=169.56(元)
教材第106页“应用与反思”第18题
4.一段圈柱形钢材长2米,截西面积是9平方分米,每立方分米钢重7.8千克。这段钢材有多重
2米=20分米
9×20×7.8=1404(千克)
答:这段钢材重1404千克。
教材第106页“应用与反思”第19题
5.用一根铁丝刚好可以焊接成一个棱长是6厘米的正方体框架。如果用这根铁丝焊接成一个长5厘米、宽4厘米的长方体,它的高是多少厘米
6×12=72(厘米)
72÷4-5-4=9(厘米)
答:它的高是9厘米。
教材第106页“应用与反思”第20题
6.一个长方体苹果箱的规格是40×30×25 (单位: cm),它的体积是多少立方厘米 制作10个这样的纸箱至少需要多少纸板
这个苹果箱的体积:40×30×25=30000(立方厘米)
制作10个这样的纸箱需要纸板:
(40×30+40×25+25×30)×2×10=59000(平方厘米)
59000平方厘米=5.9平方米
答:制作10个这样的纸箱至少需要5.9平方米。
教材第107页“应用与反思”第21题
7.一个长方体的鱼缸长40厘米,宽30厘米。现将一只乌龟放入缸中完全浸没,水面上升0.8厘米。乌龟的体积是多少
40×30×0.8=960(立方厘米)
答:乌龟的体积是960立方厘米。
教材第107页“应用与反思”第22题
8. 把一块长12米的长方体木材锯成完全相同的两块小长方体(如图),表面积增加了0.9平方米。这根木材原来体积是多少立方米
0.9÷2×12=5.4(立方米)
答:这根木材原来的体积是5.4立方米。
教材第107页“应用与反思”第25题
9.制作一个圆柱形灯罩(上下无底,如左图),至少需要多少平方厘米的材料
3.14×40×20=2512(平方厘米)
答:至少需要2512平方厘米的材料。
10.如下图,一个圆锥的高是3 cm,沿着它的高平均切成两部分,表面积就增加12 cm2,原来圆锥的底面直径是( )cm。
4
增加的部分是两个相同的三角形,增加部分的面积=底面直径×高。
12÷3=4(cm)
教材第107页“应用与反思”第26题
11.一罐辣酱(如右图),从里面量底面直径为6厘米,高10厘米。如果每立方厘米辣酱重约1.1克,这瓶辣酱大约重多少克 ( 得数保留整百克)
3.14×(6÷2)2×10×1.1≈300(克)
答:这瓶辣酱大约重300克。
教材第107页“应用与反思”第27题
12.一个正方体水箱的棱长是4分米。如果将一个体积是3.2立方分米的石块浸入水中,水面上升多少厘米
3.2÷(4×4)=0.2(分米)
0.2分米=2厘米
答:水面上升2厘米。
教材第107页“应用与反思”第28题
13.一个圆锥形状的小麦堆,底面周长是25.12米,高是3米。每立方米小麦大约重760千克,这堆小麦大约重多少吨 (得数保留整数)
25.12÷3.14÷2=4(米)
×3.14××3×760=38182.4(千克)
38182.4千克=38.1824吨≈38吨
答:这堆小麦大约重38吨。。
教材第108页“应用与反思”第29题
14.用一块圆木制作一个陀螺(如右图)削去部分的体积是多少立方厘米
3.14×(6÷2)2×(10-7) ×(1- )
=3.14×9×3×
=56.52()
答:削去部分的体积是56.52立方厘米。
7cm
10cm
6cm
教材第108页“应用与反思”第30题
15.一个底面直径是4分米的圆柱形木桶,高5分米。这个木桶破损后(如左图)最多能盛多少升水
5厘米=0.5分米
3.14×(4÷2)2×(5-0.5)=56.52(立方分米)
56.52立方分米=56.52升
答:最多能盛56.52升。
教材第108页“应用与反思”第31题
16.用下面的五块玻璃做一个鱼缸,这个鱼缸的底面积是多少 它能装多少升水 ( 玻璃的厚度不计)
底面积:4.5×2=9()
容 积:4.5×2×1.5=13.5()=13.5升
答:这个鱼缸的底面积是9平方分米,能装13.5升水。
1.5dm
4.5dm
4.5dm
2dm
2dm
2dm
1.5dm
4.5dm
1.5dm
1.5dm
教材第108页“应用与反思”第32题
17.商店运来12箱啤酒,把它们堆放成长方体形状,它们的占地面积可能是多少平方分米
要堆放成长方体形状,可以有很多种状况:
2
12箱
3
这三种情况都是12个箱子接触地面,所以占地面积一样,我们把它们视为一种情况。
1
教材第108页“应用与反思”第32题
……
12箱
1
2
4×3=12(平方分米)
要堆放成长方体形状,有以下6类状况:
4×3×2=24(平方分米)
教材第108页“应用与反思”第32题
4×3×3=36(平方分米)
4×3×4=48(平方分米)
3
4
教材第108页“应用与反思”第32题
5
6
4×3×6=72(平方分米)
4×3×12=144(平方分米)
教材第108页“应用与反思”第33题
18.瓶子里装着一些水(如下图),瓶底面积是0.8平方分米。请你想办法计算瓶子的容积。
转化可以使复杂的问题变得简单。
可以把不规则图形转化成规则图形来研究。
0.8×
=0.8×2.6
=2.08(立方分米)
=2.08(升)
作业课件中的相关练习。
02
01
课后练习题。
课后作业
第3课时 立体图形的认识与测量
青岛版数学六年级(下)
二 图形与几何
1.图形的认识与测量
知识梳理
需要回顾整理的内容有哪些呢?
表面积、体积的推导及计算
要点回顾
知识点1:立体图形的特征
名称 相同点 不同点 联系
面 棱 顶点 面的形状 面的大小 棱长 长方体
正方体
6个
12条
8个
6个面都是长方形(特殊的有两个相对的面是正方形)
6个面都是正方形
相对面的面积相等
6个面的面积都相等
相对的4条棱长度相等
12条棱的长度都相等
正方体是特殊的长方体
名称 特征
圆柱
圆锥
有3个面:上、下底面是相等的两个圆,侧面是曲面。
有2个面:底面是圆,侧面是曲面。
两个底面之间的距离叫做高,有无数条长度相等的高。
顶点到底面圆心的距离叫做高,只有一条高。
侧面沿高剪开,展开后是长方形(正方形)。
侧面展开后可以得到一个扇形。
由长方形(正方形)的一边为轴旋转一周可以形成。
由直角三角形的一条直角边为轴旋转一周可以形成。
当长方体的长、宽、高相等时,就变成了正方体。
正方体是特殊的长方体。
长方体
正方体
立体图形之间的关系
当圆柱的上底面的面积等于 0 时,就变成了圆锥。
知识点2:立体图形的表面积
把长方体沿棱剪开,展开得到6个长方形,长方体的表面积就是这6个长方形的面积和。
长方体的表面积=(长×宽+长×高+宽×高)×2
S=2(ab+ah+bh)
a
b
h
a
b
h
前
后
左
右
上
下
把正方体沿棱剪开,展开得到6个完全相同的正方形,正方体的表面积就是其中一个面面积的6倍。
正方体的表面积=棱长的平方×6
S=6a2
a
a
a
a
前
后
左
右
上
下
a
a
把圆柱沿高和底面圆周剪开,侧面是一个长方形(正方形),圆柱的表面积就是三个面面积的和。
圆柱的表面积=底面积×2+底面周长×高
S=S侧+2S底=2πrh+2πr2
r
h
C
侧面
上底
下底
h
知识点3:立体图形的体积
用棱长为1 cm的小正方体摆成不同的长方体,长方体所含小正方体的数量就是长方体的体积。
长方体的体积=长×宽×高 V=abh
a
b
h
正方体是长、宽、高都相等的特殊的长方体。
正方体的体积=棱长的立方 V=a3
a
a
a
把圆柱沿底面直径切成若干等份,可以拼成一个近似的长方体,圆柱的底面积等于长方体的底面积,圆柱的高等于长方体的高。
圆柱的体积=底面积×高 V=πr2h
把圆锥形容器里的沙子倒入与它等底、等高的圆柱形容器内,3次才能倒满。
圆锥的体积=与圆锥等底、等高的圆柱的体积×-
V=-S底h=-πr2h
13
13
13
a
b
h
a
a
a
h
h
S
S
V=
ɑbh
V=
ɑ·ɑ·ɑ=ɑ
V =
Sh
V=
Sh
V = Sh
S
h
S
这些体积计算公式之间有怎样的联系呢?
知识点4:立体图形的应用
62.8cm
31.4cm
20cm
10cm
15.7cm
7.85cm
选择上面的材料制作一个水桶,有几种方案
联系已有知识经验想象水桶的形状
水桶的形状可能是长方体的,也可能是圆柱体的。
长方体水桶的侧面展开图是长方形,底面是正方形。
圆柱体水桶的侧面展开图是长方形,底面是圆形。
应选择长方形和正方形材料制作这样的水桶。
长方形的长或宽等于底面的周长。
选择长方形和圆形材料制作这个水桶。
长方形的长或宽等于底面的周长。
正方形边长:62.8÷4=15.7(厘米)
62.8cm的边作为底面周长。
可以选择长62.8cm、宽31.4cm的长方形做水桶侧面,边长为15.7cm的正方形做水桶的底。
制作长方体水桶
正方形边长:31.4÷4=7.85(厘米)
31.4cm的边作为底面周长。
可以选择长62.8cm、宽31.4cm的长方形做水桶侧面,边长为7.85cm的正方形做水桶的底。
底面直径:62.8÷3.14=20(厘米)
62.8cm的边作为底面周长。
可以选择长62.8cm、宽31.4cm的长方形做水桶侧面,底面直径为20cm的圆做水桶的底。
制作圆柱体水桶
底面直径:31.4÷3.14=10(厘米)
31.4cm的边作为底面周长。
可以选择长62.8cm、宽31.4cm的长方形做水桶侧面,底面直径为10cm的圆做水桶的底。
10cm
问题:怎样选择材料制作水桶
联系已有知识经验想象水桶的形状
水桶的侧面展开图是长方形
水桶的底面是圆形(或正方形)
选择长方形和圆形(或正方形)材料
长方形的长或宽等于底面的周长
形成制作水桶的方案
平面
立体
立体
总结一下这个问题的解决过程吧!
课堂练习
教材第105页“应用与反思”第14题
1. 我说你搭。
现在,请你在两个圆柱形积木的上面搭一块与底座的长和宽都相等的长方体积木.....
我从长方体积木中找,长和宽.....
小阳
小刚
教材第105页“应用与反思”第14题
(1)小阳应该怎样准确地描述呢
先要说清楚积木的形状和大小,再说清楚它的位置。
(2)小刚是怎样找到他需要的积木并确定它的位置的
先根据描述想象出符合要求的图形,找到相应的积木,再搭建要求的形状。
教材第106页“应用与反思”第16题
2.如果从正面和上面看到的都是右面的图形,你知道小正方体是怎样摆放的吗 摆摆看。
教材第106页“应用与反思”第17题
3.用铁皮做60个长为50厘米、底面半径为3厘米的圆柱形通风管。如果每平方米铁皮30元,做这些通风管需花多少钱
2×3.14×3×50×60=56520(平方厘米)
答:需要花169.56元。
56520平方厘米=5.652平方米
30×5.652=169.56(元)
教材第106页“应用与反思”第18题
4.一段圈柱形钢材长2米,截西面积是9平方分米,每立方分米钢重7.8千克。这段钢材有多重
2米=20分米
9×20×7.8=1404(千克)
答:这段钢材重1404千克。
教材第106页“应用与反思”第19题
5.用一根铁丝刚好可以焊接成一个棱长是6厘米的正方体框架。如果用这根铁丝焊接成一个长5厘米、宽4厘米的长方体,它的高是多少厘米
6×12=72(厘米)
72÷4-5-4=9(厘米)
答:它的高是9厘米。
教材第106页“应用与反思”第20题
6.一个长方体苹果箱的规格是40×30×25 (单位: cm),它的体积是多少立方厘米 制作10个这样的纸箱至少需要多少纸板
这个苹果箱的体积:40×30×25=30000(立方厘米)
制作10个这样的纸箱需要纸板:
(40×30+40×25+25×30)×2×10=59000(平方厘米)
59000平方厘米=5.9平方米
答:制作10个这样的纸箱至少需要5.9平方米。
教材第107页“应用与反思”第21题
7.一个长方体的鱼缸长40厘米,宽30厘米。现将一只乌龟放入缸中完全浸没,水面上升0.8厘米。乌龟的体积是多少
40×30×0.8=960(立方厘米)
答:乌龟的体积是960立方厘米。
教材第107页“应用与反思”第22题
8. 把一块长12米的长方体木材锯成完全相同的两块小长方体(如图),表面积增加了0.9平方米。这根木材原来体积是多少立方米
0.9÷2×12=5.4(立方米)
答:这根木材原来的体积是5.4立方米。
教材第107页“应用与反思”第25题
9.制作一个圆柱形灯罩(上下无底,如左图),至少需要多少平方厘米的材料
3.14×40×20=2512(平方厘米)
答:至少需要2512平方厘米的材料。
10.如下图,一个圆锥的高是3 cm,沿着它的高平均切成两部分,表面积就增加12 cm2,原来圆锥的底面直径是( )cm。
4
增加的部分是两个相同的三角形,增加部分的面积=底面直径×高。
12÷3=4(cm)
教材第107页“应用与反思”第26题
11.一罐辣酱(如右图),从里面量底面直径为6厘米,高10厘米。如果每立方厘米辣酱重约1.1克,这瓶辣酱大约重多少克 ( 得数保留整百克)
3.14×(6÷2)2×10×1.1≈300(克)
答:这瓶辣酱大约重300克。
教材第107页“应用与反思”第27题
12.一个正方体水箱的棱长是4分米。如果将一个体积是3.2立方分米的石块浸入水中,水面上升多少厘米
3.2÷(4×4)=0.2(分米)
0.2分米=2厘米
答:水面上升2厘米。
教材第107页“应用与反思”第28题
13.一个圆锥形状的小麦堆,底面周长是25.12米,高是3米。每立方米小麦大约重760千克,这堆小麦大约重多少吨 (得数保留整数)
25.12÷3.14÷2=4(米)
×3.14××3×760=38182.4(千克)
38182.4千克=38.1824吨≈38吨
答:这堆小麦大约重38吨。。
教材第108页“应用与反思”第29题
14.用一块圆木制作一个陀螺(如右图)削去部分的体积是多少立方厘米
3.14×(6÷2)2×(10-7) ×(1- )
=3.14×9×3×
=56.52()
答:削去部分的体积是56.52立方厘米。
7cm
10cm
6cm
教材第108页“应用与反思”第30题
15.一个底面直径是4分米的圆柱形木桶,高5分米。这个木桶破损后(如左图)最多能盛多少升水
5厘米=0.5分米
3.14×(4÷2)2×(5-0.5)=56.52(立方分米)
56.52立方分米=56.52升
答:最多能盛56.52升。
教材第108页“应用与反思”第31题
16.用下面的五块玻璃做一个鱼缸,这个鱼缸的底面积是多少 它能装多少升水 ( 玻璃的厚度不计)
底面积:4.5×2=9()
容 积:4.5×2×1.5=13.5()=13.5升
答:这个鱼缸的底面积是9平方分米,能装13.5升水。
1.5dm
4.5dm
4.5dm
2dm
2dm
2dm
1.5dm
4.5dm
1.5dm
1.5dm
教材第108页“应用与反思”第32题
17.商店运来12箱啤酒,把它们堆放成长方体形状,它们的占地面积可能是多少平方分米
要堆放成长方体形状,可以有很多种状况:
2
12箱
3
这三种情况都是12个箱子接触地面,所以占地面积一样,我们把它们视为一种情况。
1
教材第108页“应用与反思”第32题
……
12箱
1
2
4×3=12(平方分米)
要堆放成长方体形状,有以下6类状况:
4×3×2=24(平方分米)
教材第108页“应用与反思”第32题
4×3×3=36(平方分米)
4×3×4=48(平方分米)
3
4
教材第108页“应用与反思”第32题
5
6
4×3×6=72(平方分米)
4×3×12=144(平方分米)
教材第108页“应用与反思”第33题
18.瓶子里装着一些水(如下图),瓶底面积是0.8平方分米。请你想办法计算瓶子的容积。
转化可以使复杂的问题变得简单。
可以把不规则图形转化成规则图形来研究。
0.8×
=0.8×2.6
=2.08(立方分米)
=2.08(升)
作业课件中的相关练习。
02
01
课后练习题。
课后作业
同课章节目录
