青岛版 数学六年级下册 总复习—四策略与方法--研究数学问题的一般步骤和方法(课件) (共13张PPT)
文档属性
| 名称 | 青岛版 数学六年级下册 总复习—四策略与方法--研究数学问题的一般步骤和方法(课件) (共13张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 576.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-01 00:00:00 | ||
图片预览


文档简介
(共13张PPT)
第3课时 研究数学问题的一般步骤和方法
青岛版数学六年级(下)
四 策略与方法
要点回顾
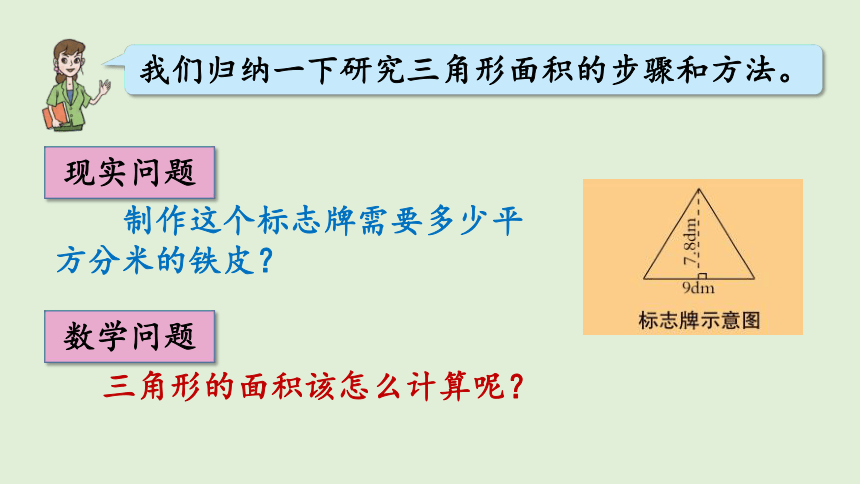
在研究三角形的面积时,我们是从解决“求标志牌的面积”入手的。
在研究平面图形的面积和立体图形的体积的计算方法时,我们经历了怎样的过程
我们用了剪拼的方法。
制作这个标志牌需要多少平方分米的铁皮?
三角形的面积该怎么计算呢?
现实问题
数学问题
我们归纳一下研究三角形面积的步骤和方法。
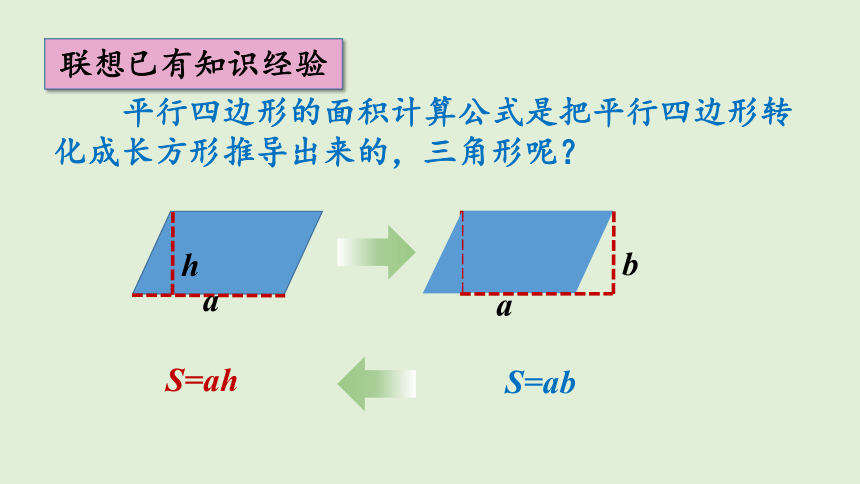
平行四边形的面积计算公式是把平行四边形转化成长方形推导出来的,三角形呢?
联想已有知识经验
a
b
a
h
S=ab
S=ah
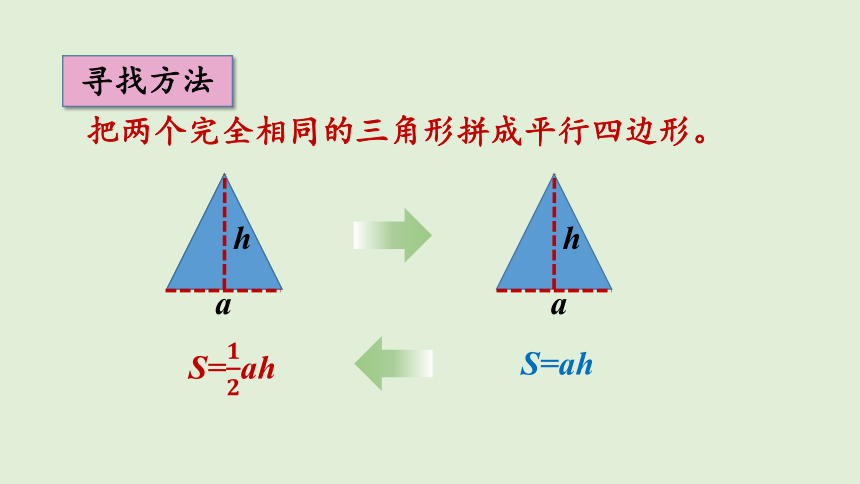
把两个完全相同的三角形拼成平行四边形。
寻找方法
a
h
a
h
S=ah
S=ah
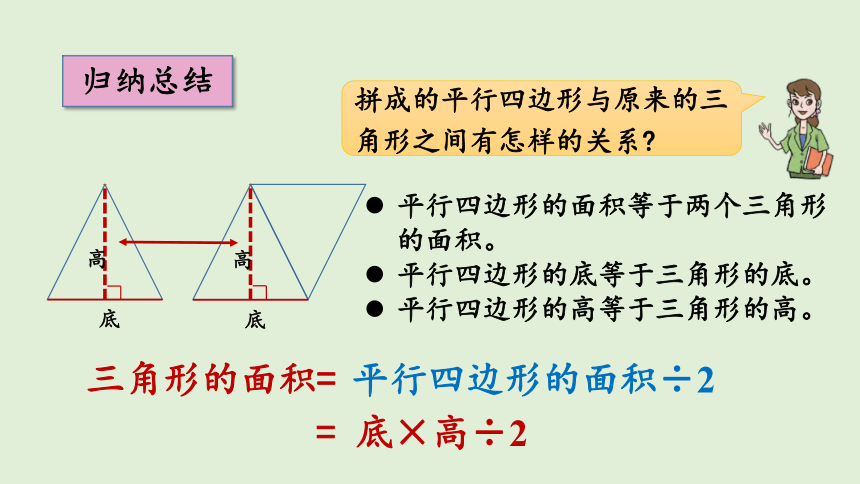
归纳总结
拼成的平行四边形与原来的三角形之间有怎样的关系
高
高
底
底
平行四边形的面积等于两个三角形的面积。
平行四边形的底等于三角形的底。
平行四边形的高等于三角形的高。
三角形的面积=
平行四边形的面积÷2
= 底×高÷2
解决问题、解释应用
制作这个标志牌需要多少平方分米的铁皮?
9×7.8÷2 =35.1(dm2)
答:制作这个标志牌需要35.1平方分米的铁皮。
在探索长方体体积的计算方法时,我们经历了以下过程。
现实问题
怎样求长方体可乐箱的体积
数学问题
怎样求长方体的体积
联想已有知识经验
由求面积的方法推想出:体积的大小就是含有体积单位的多少。
寻找方法
切一切、摆一摆、数一数、算一算。
归纳结论
实验验证、总结体积公式:
V=abh
解决问题、解释应用
运用公式求出长方体的体积,解决求可乐箱体积的问题。
产生新问题
?
我们再来回顾一下研究圆面积的过程。
现实问题
圆形中心舞台的面积是多少平方米
数学问题
怎样求圆的面积
联想已有知识经验
多边形面积公式及推导方法。
平均分成若干份,拼成一个近似的长方形。
寻找方法
分的份数越多,拼成的图形就越接近长方形。
归纳结论
实验验证、
总结公式:
解决问题
解释应用
运用公式求出圆形中心舞台的面积。
产生新问题
?
课堂练习
1.学校圆形花坛被平均分成6份,种植了叶子花(红色)和黄杨(绿色),花坛的半径为4米,如果每平方米摆10盆,一共需要多少盆黄杨?(π取3)
联想已有知识经验
圆面积的计算公式
寻找方法
半圆的面积等于圆面积的一半。
现实问题
一共需要多
少盆黄杨?
数学问题
怎样计算半
圆的面积?
一共需要多少盆黄杨?
0.5×3×42×10=240(盆)
解决问题、解释应用
如何求扇形的面积?
产生新问题
归纳结论
S半=0.5πr2
2.一支铺路队正在铺一段公路。上午工作3.5小时,铺了164.9m;下午工作4.5 小时,铺了206.7m。是上午铺路的速度快,还是下午铺路的速度快?
联想已有知识经验
工作效率=工作总量÷工作时间
寻找方法
先计算、再比较。
现实问题
上午速度快,
还是下午?
数学问题
比较工作效率
解决问题、解释应用
归纳结论
若上午工作效率大于
下午工作效率,
则上午速度快。
反之,下午快。
164.9÷3.5 ≈ 47(米/时)
206÷4.5 ≈ 46(米/时)
47>46,
所以上午铺路的速度快。
第3课时 研究数学问题的一般步骤和方法
青岛版数学六年级(下)
四 策略与方法
要点回顾
在研究三角形的面积时,我们是从解决“求标志牌的面积”入手的。
在研究平面图形的面积和立体图形的体积的计算方法时,我们经历了怎样的过程
我们用了剪拼的方法。
制作这个标志牌需要多少平方分米的铁皮?
三角形的面积该怎么计算呢?
现实问题
数学问题
我们归纳一下研究三角形面积的步骤和方法。
平行四边形的面积计算公式是把平行四边形转化成长方形推导出来的,三角形呢?
联想已有知识经验
a
b
a
h
S=ab
S=ah
把两个完全相同的三角形拼成平行四边形。
寻找方法
a
h
a
h
S=ah
S=ah
归纳总结
拼成的平行四边形与原来的三角形之间有怎样的关系
高
高
底
底
平行四边形的面积等于两个三角形的面积。
平行四边形的底等于三角形的底。
平行四边形的高等于三角形的高。
三角形的面积=
平行四边形的面积÷2
= 底×高÷2
解决问题、解释应用
制作这个标志牌需要多少平方分米的铁皮?
9×7.8÷2 =35.1(dm2)
答:制作这个标志牌需要35.1平方分米的铁皮。
在探索长方体体积的计算方法时,我们经历了以下过程。
现实问题
怎样求长方体可乐箱的体积
数学问题
怎样求长方体的体积
联想已有知识经验
由求面积的方法推想出:体积的大小就是含有体积单位的多少。
寻找方法
切一切、摆一摆、数一数、算一算。
归纳结论
实验验证、总结体积公式:
V=abh
解决问题、解释应用
运用公式求出长方体的体积,解决求可乐箱体积的问题。
产生新问题
?
我们再来回顾一下研究圆面积的过程。
现实问题
圆形中心舞台的面积是多少平方米
数学问题
怎样求圆的面积
联想已有知识经验
多边形面积公式及推导方法。
平均分成若干份,拼成一个近似的长方形。
寻找方法
分的份数越多,拼成的图形就越接近长方形。
归纳结论
实验验证、
总结公式:
解决问题
解释应用
运用公式求出圆形中心舞台的面积。
产生新问题
?
课堂练习
1.学校圆形花坛被平均分成6份,种植了叶子花(红色)和黄杨(绿色),花坛的半径为4米,如果每平方米摆10盆,一共需要多少盆黄杨?(π取3)
联想已有知识经验
圆面积的计算公式
寻找方法
半圆的面积等于圆面积的一半。
现实问题
一共需要多
少盆黄杨?
数学问题
怎样计算半
圆的面积?
一共需要多少盆黄杨?
0.5×3×42×10=240(盆)
解决问题、解释应用
如何求扇形的面积?
产生新问题
归纳结论
S半=0.5πr2
2.一支铺路队正在铺一段公路。上午工作3.5小时,铺了164.9m;下午工作4.5 小时,铺了206.7m。是上午铺路的速度快,还是下午铺路的速度快?
联想已有知识经验
工作效率=工作总量÷工作时间
寻找方法
先计算、再比较。
现实问题
上午速度快,
还是下午?
数学问题
比较工作效率
解决问题、解释应用
归纳结论
若上午工作效率大于
下午工作效率,
则上午速度快。
反之,下午快。
164.9÷3.5 ≈ 47(米/时)
206÷4.5 ≈ 46(米/时)
47>46,
所以上午铺路的速度快。
同课章节目录
