总复习—统计与可能性(课件) 数学 六年级下册青岛版(共44张PPT)
文档属性
| 名称 | 总复习—统计与可能性(课件) 数学 六年级下册青岛版(共44张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-01 07:42:35 | ||
图片预览









文档简介
(共44张PPT)
青岛版数学六年级(下)
三 统计与概率
统计与可能性
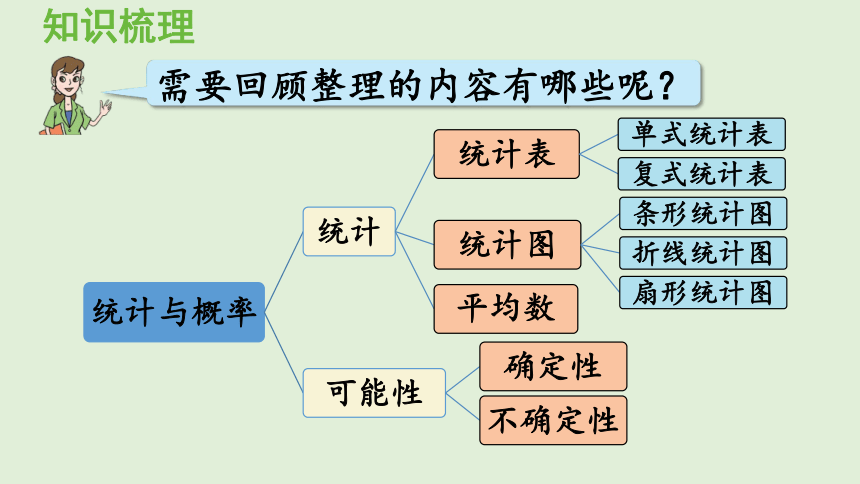
知识梳理
需要回顾整理的内容有哪些呢?
要点回顾
知识点1:数据的收集与整理
确定调查的主题和需要调查的数据。
1
根据调查的主题和数据设计调查表和统计表。
2
确定调查方法。
3
进行调查,确定记录数据的方法,并做好记录。
4
整理和描述数据,选择适当的统计图表表示数据。
5
根据统计图表分析数据,作出判断和预测。
6
用调查法收集整理和分析数据的步骤:
知识点2:统计表
意义:把收集到的数据经过分类、整理后,填在一定格式的表格内,用来反映情况,说明问题,这种表格叫做统计表。
统计表
单式统计表
复式统计表
只含有一组统计项目。
含有两组或两组以上统计项目。
统计表可以清晰地看出数据的大小。
收集、整理数据。
1
确定统计表的格式和栏目数量制成表格。
2
填写栏目和各项目名称,并根据整理好的数据填表。
3
计算总计和合计,并填入表中。
4
写好统计表的名称和制表时间。
5
绘制统计表的一般步骤:
尺码 35 36 37 38 39 40
进货数量/双 30 100 150 90 50 20
尺码 35 36 37 38 39 40
销售数量/双 16 94 145 83 30 10
尺码 35 36 37 38 39 40
进货数量/双 30 100 150 90 50 20
销售数量/双 16 94 145 83 30 10
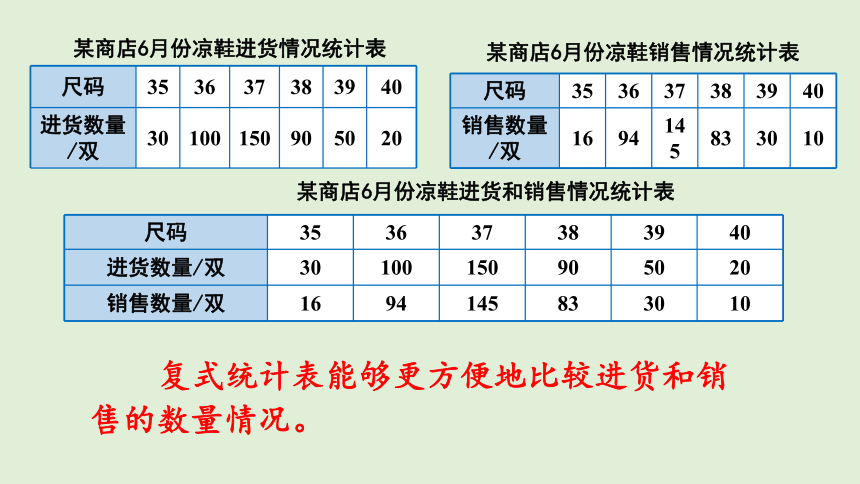
某商店6月份凉鞋进货情况统计表
某商店6月份凉鞋销售情况统计表
某商店6月份凉鞋进货和销售情况统计表
复式统计表能够更方便地比较进货和销售的数量情况。
知识点3:统计图
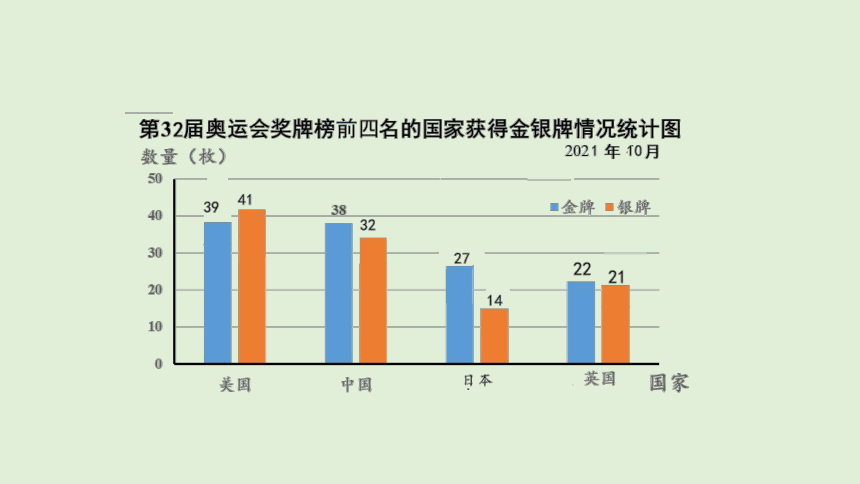
条形统计图:
用一个单位长度表示一定数量。
1
用直条的长短表示数量的多少。
2
单式条形统计图
复式条形统计图
分类:
特点:
能清楚、直观地表示出各数量的多少,便于相互比较。
根据图纸的大小,画出两条相互垂直的射线。
1
在水平射线上,分配直条的位置,确定直条的宽度和间隔。
2
在竖直射线上,根据数据大小的具体情况,确定单位长度。
3
按照数据的大小,画出长短不同的直条,并标明数据。
4
写上统计图的名称及制图日期。
5
绘制条形统计图的一般步骤:
折线统计图:
用一个单位长度表示一定数量。
1
用折线的起伏表示数量的增减变化。
2
单式折线统计图
复式折线统计图
分类:
特点:
不仅可以看出各数量的多少,而且可以看出数量的增减变化情况。
根据图纸的大小,画出两条相互垂直的射线。
1
在水平射线上,分配各点的位置,确定点的间隔。
2
在竖直射线上,根据数据大小的具体情况,确定单位长度。
3
按照数据的大小描出各点,顺次连接,并标明数据。
4
写上统计图的名称及制图日期。
5
绘制折线统计图的一般步骤:
扇形统计图:
用整个圆的面积表示总数量(单位1)。
1
用圆内的扇形面积表示各部分占总数量的百分数。
2
特点:
能清楚地反映出各部分数量占总数量的百分比;能看出部分与整体、部分与部分之间的关系。
种类 条形统计图 折线统计图 扇形统计图
特点 能清楚的看出数量的多少 便于比较 不但能看出各种数量的多少,还能看出数量的增减变化趋势 能清楚的表示出部分和总量之间的关系
三类统计图特点的比较:
根据需要,结合三类统计图的特点,我们可以合理地选择统计图来描述和分析数据。
知识点4:平均数
一组数据的和除以这组数据的个数,所得的商叫做平均数。
平均数反映一组数据的平均大小,常用来代表数据的总体“平均水平”。
平均数=总数量÷总份数
总数量=平均数×总份数
下面是六年级二班10个学生的数学考试成绩,请你计算出他们的平均分。
72 85 69 88 96 51 65 89 69 54
平均分=(72+85+69+88+93+51+65+89+69+54)÷10
=73.8(分)
答:这10个同学的平均成绩为73.5分。
知识点5:可能性
一定
可能
经常
偶尔
不可能
在某种情况下可能发生,也可能不发生的事件,是不确定事件。
在任何情况下都会发生的事件。
在任何情况下都不会发生的事件。
确定
事件
常用哪些词来描述事情发生的可能性?
确定的
不确定的
2024年2月有29天
2024年为367天
明天下雨
从一副扑克牌中随机抽出一张牌,为K。
一定发生
一定不发生
有可能发生
有可能发生
可能性的大小:
事情发生的可能性的大小与个体数量有关。
可能性大
个体数量多
一定
可能性小
个体数量少
不可能
游戏规则的公平性是指参与游戏活动的各方获胜的可能性是相等的。
游戏各方机会均等
游戏规则公平
游戏各方机会不等
游戏规则不公平
可以根据事件发生的可能性大小来设计游戏规则。
游戏规则的公平性:
盒子中有红、黑、白三种球,从中随机取出一个,取出的会是什么颜色的球呢?
颜色
数量
可能性
3
7
11
很小
小
很大
取出红、黑、白任何一种颜色的球都是可能的。但是盒中白色的球最多,所以取出的球是白色的可能性最大;盒中黑色的球最少,所以取出的球是黑色的可能性最小。
课堂练习
(2)该小学全年级的及格率是( )%。
(1)优秀人数比良好人数少( )%。
50
1.下面是某小学六年级同学参加“体质健康标准”测试成绩统计表。
(80-40)÷80=50%
等级 优秀 良好 及格 不及格
人数 40 80 30 10
93.75
(80+40+30)÷(80+40+30+10)=150÷160
=93.75%
2. 六年级二班同学平均每天看电视的时间如下表。
1小时以下 1~2小时 2小时以上
近视的同学 3 8 18
不近视的同学 12 8 5
时间
人数(人)
项目
如果要描述全班同学平均每天看电视所用的时间情况,选用哪种统计,图比较合适 请将统计图补充完整。
条形统计图能反映统计量的多少。
3.下面是A、B两个旅游景点去年接待游客的情况统计图。
6
5
4
3
2
1
0
数量/万人
A景点 B景点
第一季度 第二季度 第三季度 第四季度 季度
2.5
1.2
5
2
6
3.5
4.5
3
6
5
4
3
2
1
0
数量/万人
A景点 B景点
第一季度 第二季度 第三季度 第四季度 季度
2.5
1.2
5
2
6
3.5
4.5
3
(1)A、B两个景点的游客数量相差最多的是第( )季度,相差( )万人。
二
3
5-2=3(万人)
6
5
4
3
2
1
0
数量/万人
A景点 B景点
第一季度 第二季度 第三季度 第四季度 季度
2.5
1.2
5
2
6
3.5
4.5
3
(2)A景点平均每季度接待游客( )万人。
4.5
(2.5+5+6+4.5)÷4=4.5(万人)
6
5
4
3
2
1
0
数量/万人
A景点 B景点
第一季度 第二季度 第三季度 第四季度 季度
2.5
1.2
5
2
6
3.5
4.5
3
(3)B景点第三季度接待游客的人数比第二季度增加了( )%。
75
(3.5-2)÷2=75%
教材第113页“应用与反思”第2题
4.合理的饮食习惯是身体健康的重要保证。专家通过研究,制定出了适合我国居民的平衡膳食结构图。
(1)从扇形统计图中你获得了哪些信息
根据我国居民的平衡膳食结构图,我们每日吃掉的食物中,油脂类应占1% ,奶类和豆类应占12% ,鱼、禽、肉、蛋类占16%,蔬菜和水果类应占24% ,谷类应占47%。
教材第113页“应用与反思”第2题
(2)下面是小强某一天的饮食情况统计表,请把表格填完整。(用计算器计算)
种类 各类食物摄入量(克) 各类食物摄入量占总摄入量的百分比 各类食物摄入量应占总摄入量的百分比
油脂类 37
奶类和豆类 150
鱼、禽、肉、蛋类 400
蔬菜和水果类 200
谷类 500
2.87%
1%
11.66%
12%
31.08%
16%
15.54%
24%
38.85%
47%
教材第113页“应用与反思”第2题
(3)观察表中的数据,说一说小强这一天的膳食合理吗。你有什么建议
小强这一天的膳食不合理。他的鱼、禽、肉、蛋类摄入量超过了我国居民平衡膳食结构的推荐值。蔬菜和水果类、谷类食物的摄入量又低于我国居民平衡膳食结构的推荐值。
建议:减少油脂类、鱼、禽、肉、蛋类食物的摄入量,增加蔬菜和水果类、谷类食物的摄入量。
5.在某市举行的青年歌手大奖赛中,11位评委给一位歌手的打分如下。
平均数=总数量÷总份数
(1)这组数据的平均数是多少?
(9.8+9.7×2+9.6×4+9.5+9.4×2+9.1)÷11
=105÷11
≈9.55
答:这组数据的平均数是9.55。
9.8 9.7 9.7 9.6 9.6 9.6 9.6 9.5 9.4 9.4 9.1
(2)如果按照“去掉一个最高分,去掉一个最低分,再计算平均分”的评分方法来计算,平均分是多少?
(9.7×2+9.6×4+9.5+9.4×2)÷9
=86.1÷9
≈9.57
答:平均分是9.57分。
9.8 9.7 9.7 9.6 9.6 9.6 9.6 9.5 9.4 9.4 9.1
5.在某市举行的青年歌手大奖赛中,11位评委给一位歌手的打分如下。
答:我认为有道理。因为平均数与一组数据中每个数据都有关系,易受极端数字的影响;在评分时去掉一个最高分和一个最低分,再计算平均数可以减小这种影响。
9.8 9.7 9.7 9.6 9.6 9.6 9.6 9.5 9.4 9.4 9.1
你认为这样做是否有道理?为什么?
(2)如果按照“去掉一个最高分,去掉一个最低分,再计算平均分”的评分方法来计算,平均分是多少?
5.在某市举行的青年歌手大奖赛中,11位评委给一位歌手的打分如下。
6.填一填。
(1)盒子里有9个红色棋子,2个黄色棋子。任意摸出1个,可能出现( )种情况,摸出( )色棋子的可能性大。
两
数量多 → 可能性大
数量少 → 可能性小
比较可能性的大小
红
红色棋子9个>黄色棋子2个
(2)掷两粒骰子,出现点数和为7的可能性比为8的可能性( )(填“大”或“小”)。
点数和为7的情况: 和 、 和 、 和 、
和 、 和 、 和 共6种。
点数和为8的情况: 和 、 和 、 和 、
和 、 和 共5种。
大
(3)有11张卡片,分别写着1~11这11个数,小明从中任意抽取一张,他抽到奇数的可能性( )抽到偶数的可能性。(填“大于”“小于”或“等于”)。
11张卡片中奇数有:1、3、5、7、9、11,共6张;
偶数有:2、4、6、8、10,共5张。
大于
1
2
3
4
5
6
7
8
9
10
11
7.选择。
数字“1”和“2”出现的次数很接近,转盘上所占面积大小很接近的转盘最有可能。
(1)游戏室有一些转盘,上面分别标有数字“1”和“2”。小云转动其中一个转盘共58次,其中“1”出现30次,“2”出现28次,小云转的转盘最有可能是( )。
B
A. B. C. D.
1
2
1
1
1
2
2
2
2
1
→
→
→
→
天气情况属于不确定事件,“一定”一般用于确定事件。预报中说“局部地区可能有小雨”说明明天下雨的可能性大。
(2)某天气预报中说“我市明天晴转多云,局部地区可能有小雨”,根据这一预报,下面各说法中,正确的是( )。
C
A. 明天一定下雨 B. 明天一定不下雨
C. 明天下雨的可能性大 D. 明天下雨的可能性小
(3)甲、乙两人进行摸球比赛,甲摸到黄球得1分,乙摸到绿球得1分,在下面的( )箱中摸球最公平。
B
当箱中的黄球和绿球的个数相等时,游戏才公平。
A. B. C.
教材第113页“应用与反思”第3题
8.将下面这些卡片混在一起,从中任意抽取一张,这张卡片可能是什么 抽取哪种卡片的可能性大
可能是这四张卡片中的任何一张。
因为有两张泰山卡片,所以从这四张卡片中任意抽取一张,抽取到泰山卡片的可能性大。
泰山
趵突泉
孔庙
泰山
教材第113页“应用与反思”第4题
9. “甲产品的返修率为5%,乙产品的返修率为4%,两种产品的其他指标完全相同。”根据这条信息,你会选择哪一种产品 说明理由。
我会选择乙产品。
因为乙产品的返修率为4%,低于甲产品5%的返修率,这说明乙产品的品质更高,所以选择乙产品。
作业课件中的相关练习。
02
01
课后练习题。
课后作业
青岛版数学六年级(下)
三 统计与概率
统计与可能性
知识梳理
需要回顾整理的内容有哪些呢?
要点回顾
知识点1:数据的收集与整理
确定调查的主题和需要调查的数据。
1
根据调查的主题和数据设计调查表和统计表。
2
确定调查方法。
3
进行调查,确定记录数据的方法,并做好记录。
4
整理和描述数据,选择适当的统计图表表示数据。
5
根据统计图表分析数据,作出判断和预测。
6
用调查法收集整理和分析数据的步骤:
知识点2:统计表
意义:把收集到的数据经过分类、整理后,填在一定格式的表格内,用来反映情况,说明问题,这种表格叫做统计表。
统计表
单式统计表
复式统计表
只含有一组统计项目。
含有两组或两组以上统计项目。
统计表可以清晰地看出数据的大小。
收集、整理数据。
1
确定统计表的格式和栏目数量制成表格。
2
填写栏目和各项目名称,并根据整理好的数据填表。
3
计算总计和合计,并填入表中。
4
写好统计表的名称和制表时间。
5
绘制统计表的一般步骤:
尺码 35 36 37 38 39 40
进货数量/双 30 100 150 90 50 20
尺码 35 36 37 38 39 40
销售数量/双 16 94 145 83 30 10
尺码 35 36 37 38 39 40
进货数量/双 30 100 150 90 50 20
销售数量/双 16 94 145 83 30 10
某商店6月份凉鞋进货情况统计表
某商店6月份凉鞋销售情况统计表
某商店6月份凉鞋进货和销售情况统计表
复式统计表能够更方便地比较进货和销售的数量情况。
知识点3:统计图
条形统计图:
用一个单位长度表示一定数量。
1
用直条的长短表示数量的多少。
2
单式条形统计图
复式条形统计图
分类:
特点:
能清楚、直观地表示出各数量的多少,便于相互比较。
根据图纸的大小,画出两条相互垂直的射线。
1
在水平射线上,分配直条的位置,确定直条的宽度和间隔。
2
在竖直射线上,根据数据大小的具体情况,确定单位长度。
3
按照数据的大小,画出长短不同的直条,并标明数据。
4
写上统计图的名称及制图日期。
5
绘制条形统计图的一般步骤:
折线统计图:
用一个单位长度表示一定数量。
1
用折线的起伏表示数量的增减变化。
2
单式折线统计图
复式折线统计图
分类:
特点:
不仅可以看出各数量的多少,而且可以看出数量的增减变化情况。
根据图纸的大小,画出两条相互垂直的射线。
1
在水平射线上,分配各点的位置,确定点的间隔。
2
在竖直射线上,根据数据大小的具体情况,确定单位长度。
3
按照数据的大小描出各点,顺次连接,并标明数据。
4
写上统计图的名称及制图日期。
5
绘制折线统计图的一般步骤:
扇形统计图:
用整个圆的面积表示总数量(单位1)。
1
用圆内的扇形面积表示各部分占总数量的百分数。
2
特点:
能清楚地反映出各部分数量占总数量的百分比;能看出部分与整体、部分与部分之间的关系。
种类 条形统计图 折线统计图 扇形统计图
特点 能清楚的看出数量的多少 便于比较 不但能看出各种数量的多少,还能看出数量的增减变化趋势 能清楚的表示出部分和总量之间的关系
三类统计图特点的比较:
根据需要,结合三类统计图的特点,我们可以合理地选择统计图来描述和分析数据。
知识点4:平均数
一组数据的和除以这组数据的个数,所得的商叫做平均数。
平均数反映一组数据的平均大小,常用来代表数据的总体“平均水平”。
平均数=总数量÷总份数
总数量=平均数×总份数
下面是六年级二班10个学生的数学考试成绩,请你计算出他们的平均分。
72 85 69 88 96 51 65 89 69 54
平均分=(72+85+69+88+93+51+65+89+69+54)÷10
=73.8(分)
答:这10个同学的平均成绩为73.5分。
知识点5:可能性
一定
可能
经常
偶尔
不可能
在某种情况下可能发生,也可能不发生的事件,是不确定事件。
在任何情况下都会发生的事件。
在任何情况下都不会发生的事件。
确定
事件
常用哪些词来描述事情发生的可能性?
确定的
不确定的
2024年2月有29天
2024年为367天
明天下雨
从一副扑克牌中随机抽出一张牌,为K。
一定发生
一定不发生
有可能发生
有可能发生
可能性的大小:
事情发生的可能性的大小与个体数量有关。
可能性大
个体数量多
一定
可能性小
个体数量少
不可能
游戏规则的公平性是指参与游戏活动的各方获胜的可能性是相等的。
游戏各方机会均等
游戏规则公平
游戏各方机会不等
游戏规则不公平
可以根据事件发生的可能性大小来设计游戏规则。
游戏规则的公平性:
盒子中有红、黑、白三种球,从中随机取出一个,取出的会是什么颜色的球呢?
颜色
数量
可能性
3
7
11
很小
小
很大
取出红、黑、白任何一种颜色的球都是可能的。但是盒中白色的球最多,所以取出的球是白色的可能性最大;盒中黑色的球最少,所以取出的球是黑色的可能性最小。
课堂练习
(2)该小学全年级的及格率是( )%。
(1)优秀人数比良好人数少( )%。
50
1.下面是某小学六年级同学参加“体质健康标准”测试成绩统计表。
(80-40)÷80=50%
等级 优秀 良好 及格 不及格
人数 40 80 30 10
93.75
(80+40+30)÷(80+40+30+10)=150÷160
=93.75%
2. 六年级二班同学平均每天看电视的时间如下表。
1小时以下 1~2小时 2小时以上
近视的同学 3 8 18
不近视的同学 12 8 5
时间
人数(人)
项目
如果要描述全班同学平均每天看电视所用的时间情况,选用哪种统计,图比较合适 请将统计图补充完整。
条形统计图能反映统计量的多少。
3.下面是A、B两个旅游景点去年接待游客的情况统计图。
6
5
4
3
2
1
0
数量/万人
A景点 B景点
第一季度 第二季度 第三季度 第四季度 季度
2.5
1.2
5
2
6
3.5
4.5
3
6
5
4
3
2
1
0
数量/万人
A景点 B景点
第一季度 第二季度 第三季度 第四季度 季度
2.5
1.2
5
2
6
3.5
4.5
3
(1)A、B两个景点的游客数量相差最多的是第( )季度,相差( )万人。
二
3
5-2=3(万人)
6
5
4
3
2
1
0
数量/万人
A景点 B景点
第一季度 第二季度 第三季度 第四季度 季度
2.5
1.2
5
2
6
3.5
4.5
3
(2)A景点平均每季度接待游客( )万人。
4.5
(2.5+5+6+4.5)÷4=4.5(万人)
6
5
4
3
2
1
0
数量/万人
A景点 B景点
第一季度 第二季度 第三季度 第四季度 季度
2.5
1.2
5
2
6
3.5
4.5
3
(3)B景点第三季度接待游客的人数比第二季度增加了( )%。
75
(3.5-2)÷2=75%
教材第113页“应用与反思”第2题
4.合理的饮食习惯是身体健康的重要保证。专家通过研究,制定出了适合我国居民的平衡膳食结构图。
(1)从扇形统计图中你获得了哪些信息
根据我国居民的平衡膳食结构图,我们每日吃掉的食物中,油脂类应占1% ,奶类和豆类应占12% ,鱼、禽、肉、蛋类占16%,蔬菜和水果类应占24% ,谷类应占47%。
教材第113页“应用与反思”第2题
(2)下面是小强某一天的饮食情况统计表,请把表格填完整。(用计算器计算)
种类 各类食物摄入量(克) 各类食物摄入量占总摄入量的百分比 各类食物摄入量应占总摄入量的百分比
油脂类 37
奶类和豆类 150
鱼、禽、肉、蛋类 400
蔬菜和水果类 200
谷类 500
2.87%
1%
11.66%
12%
31.08%
16%
15.54%
24%
38.85%
47%
教材第113页“应用与反思”第2题
(3)观察表中的数据,说一说小强这一天的膳食合理吗。你有什么建议
小强这一天的膳食不合理。他的鱼、禽、肉、蛋类摄入量超过了我国居民平衡膳食结构的推荐值。蔬菜和水果类、谷类食物的摄入量又低于我国居民平衡膳食结构的推荐值。
建议:减少油脂类、鱼、禽、肉、蛋类食物的摄入量,增加蔬菜和水果类、谷类食物的摄入量。
5.在某市举行的青年歌手大奖赛中,11位评委给一位歌手的打分如下。
平均数=总数量÷总份数
(1)这组数据的平均数是多少?
(9.8+9.7×2+9.6×4+9.5+9.4×2+9.1)÷11
=105÷11
≈9.55
答:这组数据的平均数是9.55。
9.8 9.7 9.7 9.6 9.6 9.6 9.6 9.5 9.4 9.4 9.1
(2)如果按照“去掉一个最高分,去掉一个最低分,再计算平均分”的评分方法来计算,平均分是多少?
(9.7×2+9.6×4+9.5+9.4×2)÷9
=86.1÷9
≈9.57
答:平均分是9.57分。
9.8 9.7 9.7 9.6 9.6 9.6 9.6 9.5 9.4 9.4 9.1
5.在某市举行的青年歌手大奖赛中,11位评委给一位歌手的打分如下。
答:我认为有道理。因为平均数与一组数据中每个数据都有关系,易受极端数字的影响;在评分时去掉一个最高分和一个最低分,再计算平均数可以减小这种影响。
9.8 9.7 9.7 9.6 9.6 9.6 9.6 9.5 9.4 9.4 9.1
你认为这样做是否有道理?为什么?
(2)如果按照“去掉一个最高分,去掉一个最低分,再计算平均分”的评分方法来计算,平均分是多少?
5.在某市举行的青年歌手大奖赛中,11位评委给一位歌手的打分如下。
6.填一填。
(1)盒子里有9个红色棋子,2个黄色棋子。任意摸出1个,可能出现( )种情况,摸出( )色棋子的可能性大。
两
数量多 → 可能性大
数量少 → 可能性小
比较可能性的大小
红
红色棋子9个>黄色棋子2个
(2)掷两粒骰子,出现点数和为7的可能性比为8的可能性( )(填“大”或“小”)。
点数和为7的情况: 和 、 和 、 和 、
和 、 和 、 和 共6种。
点数和为8的情况: 和 、 和 、 和 、
和 、 和 共5种。
大
(3)有11张卡片,分别写着1~11这11个数,小明从中任意抽取一张,他抽到奇数的可能性( )抽到偶数的可能性。(填“大于”“小于”或“等于”)。
11张卡片中奇数有:1、3、5、7、9、11,共6张;
偶数有:2、4、6、8、10,共5张。
大于
1
2
3
4
5
6
7
8
9
10
11
7.选择。
数字“1”和“2”出现的次数很接近,转盘上所占面积大小很接近的转盘最有可能。
(1)游戏室有一些转盘,上面分别标有数字“1”和“2”。小云转动其中一个转盘共58次,其中“1”出现30次,“2”出现28次,小云转的转盘最有可能是( )。
B
A. B. C. D.
1
2
1
1
1
2
2
2
2
1
→
→
→
→
天气情况属于不确定事件,“一定”一般用于确定事件。预报中说“局部地区可能有小雨”说明明天下雨的可能性大。
(2)某天气预报中说“我市明天晴转多云,局部地区可能有小雨”,根据这一预报,下面各说法中,正确的是( )。
C
A. 明天一定下雨 B. 明天一定不下雨
C. 明天下雨的可能性大 D. 明天下雨的可能性小
(3)甲、乙两人进行摸球比赛,甲摸到黄球得1分,乙摸到绿球得1分,在下面的( )箱中摸球最公平。
B
当箱中的黄球和绿球的个数相等时,游戏才公平。
A. B. C.
教材第113页“应用与反思”第3题
8.将下面这些卡片混在一起,从中任意抽取一张,这张卡片可能是什么 抽取哪种卡片的可能性大
可能是这四张卡片中的任何一张。
因为有两张泰山卡片,所以从这四张卡片中任意抽取一张,抽取到泰山卡片的可能性大。
泰山
趵突泉
孔庙
泰山
教材第113页“应用与反思”第4题
9. “甲产品的返修率为5%,乙产品的返修率为4%,两种产品的其他指标完全相同。”根据这条信息,你会选择哪一种产品 说明理由。
我会选择乙产品。
因为乙产品的返修率为4%,低于甲产品5%的返修率,这说明乙产品的品质更高,所以选择乙产品。
作业课件中的相关练习。
02
01
课后练习题。
课后作业
同课章节目录
