2.3 圆柱的体积(课件)数学六年级下册 西师大版(共22张PPT)
文档属性
| 名称 | 2.3 圆柱的体积(课件)数学六年级下册 西师大版(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-01 00:00:00 | ||
图片预览





文档简介
(共22张PPT)
西师版数学六年级(下)
第3课时 圆柱的体积
圆柱和圆锥
二
1.掌握圆柱体积的计算公式,并能运用公式解决简单的实际问题。
2.理解圆柱体积计算公式的推导过程,体会转化思想在公式推导中的作用。
3.在运用公式解决问题的过程中,培养观察、猜测、分析、比较、综合的学习能力。
学习目标
【重点】
掌握圆柱体积的计算方法,并能用公式解决简单的实际问题。
【难点】
理解圆柱体积计算公式的推导过程,
体会转化思想在公式推导中的作用。
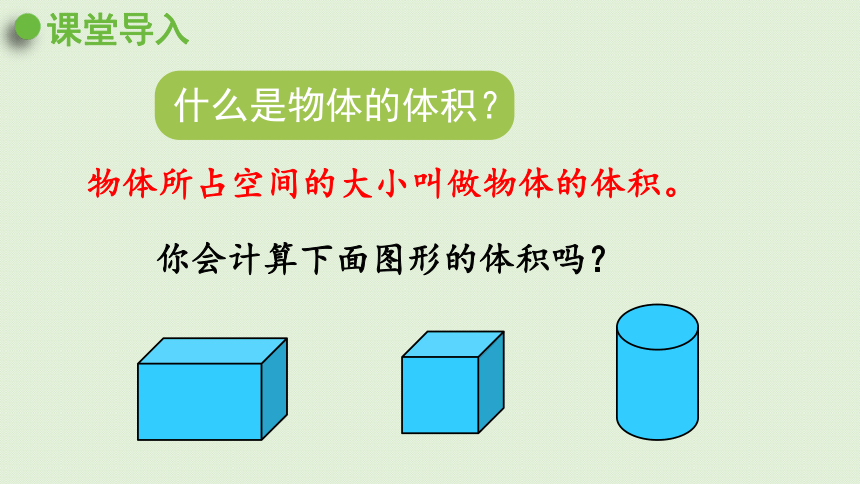
课堂导入
什么是物体的体积?
物体所占空间的大小叫做物体的体积。
你会计算下面图形的体积吗?
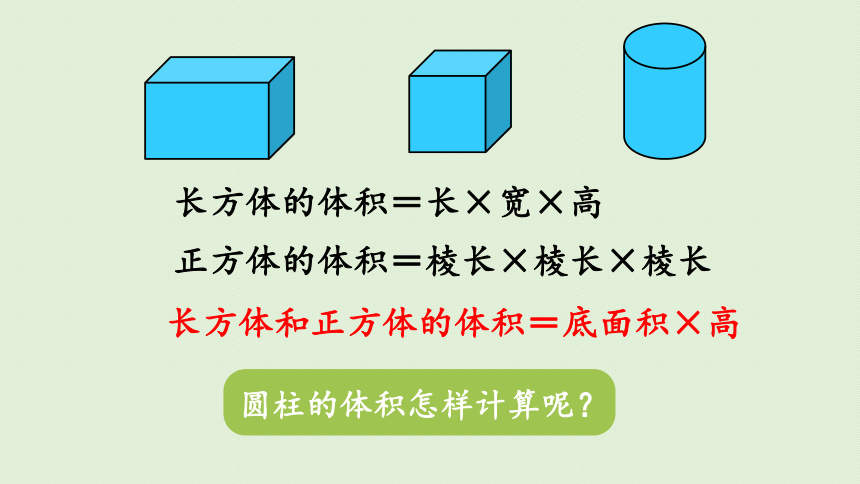
圆柱的体积怎样计算呢?
长方体的体积=长×宽×高
正方体的体积=棱长×棱长×棱长
长方体和正方体的体积=底面积×高
新知探究
我不会算圆柱的体积,
但会算长方体的体积。
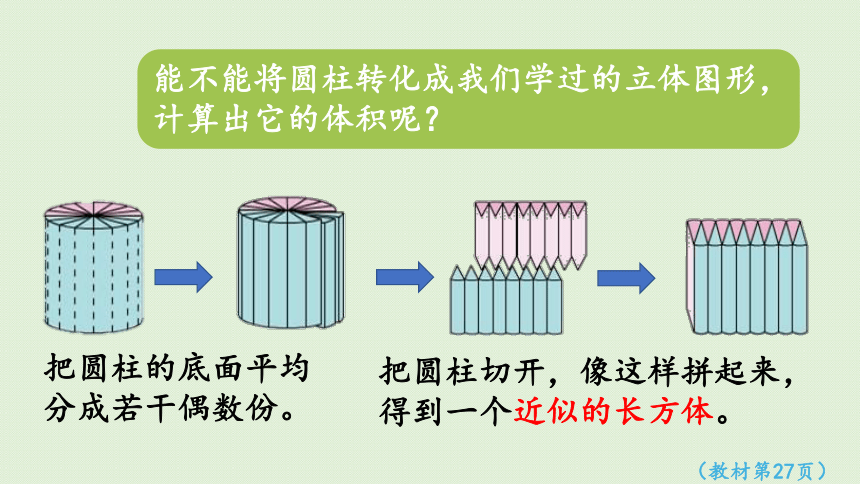
做一做,议一议:怎样计算圆柱的体积?
如果能将圆柱变成
长方体就好了。
怎样才能把圆柱转化成长方体呢?
(教材第27页)
能不能将圆柱转化成我们学过的立体图形,计算出它的体积呢?
把圆柱的底面平均分成若干偶数份。
把圆柱切开,像这样拼起来,得到一个近似的长方体。
(教材第27页)
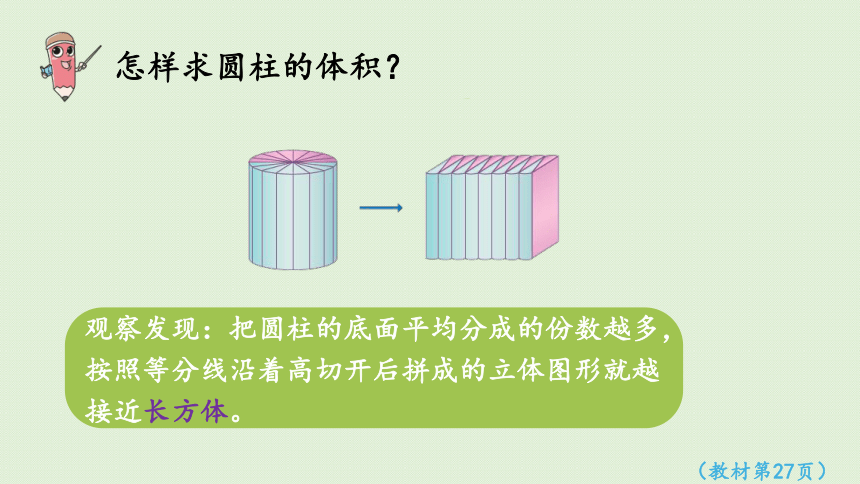
怎样求圆柱的体积?
观察发现:把圆柱的底面平均分成的份数越多,按照等分线沿着高切开后拼成的立体图形就越接近长方体。
(教材第27页)
把拼成的长方体与原来的圆柱比较,你能发现什么?
长方体的体积与圆柱的体积相等。
长方体的底面积等于圆柱的底面积,长方体的高等于圆柱的高。
(教材第27页)
总结圆柱体积的计算公式。
圆柱的体积= ×
长方体的体积= 底面积 × 高
V =
S
h
底面积
高
×
(教材第27页)
如果知道圆柱的底面半径r和高h,你能写出圆柱的体积公式吗?
圆柱的体积计算公式:
V =____________
πr h
(教材第27页)
圆柱的底面积是28.6 cm2,高15 cm,求圆柱的体积。
试一试
V = Sh
= 28.6×15
= 429(cm3)
答:圆柱的体积是429 cm3。
(教材第28页“试一试”)
这个圆柱的体积是多少立方厘米?
4
底面周长是31.4厘米。
圆柱高20厘米。
圆柱的底面半径:
圆柱的体积:
3.14×52×20=1570(cm3)
答:这个圆柱的体积是1570 cm3。
V=πr h
=5(cm)
(教材第28页例4)
课堂练习
(教材第29页练习八第1题)
1.计算体积。(图中单位:cm)
V=πr h
=3.14×52×6
=471(cm3)
1.计算体积。(图中单位:cm)
V=πr h
=3.14×2×12
=150.72(cm3)
(教材第29页练习八第1题)
1.计算体积。(图中单位:cm)
V=πr h
=3.14×(18.84÷3.14÷2)2×9
=254.34(cm3)
(教材第29页练习八第1题)
2.判断。(正确的在括号里画“√”,错误的画“×”。)
(1)计算圆柱形油桶能装多少升油就是求这个油桶的容
积。( )
(2)圆柱底面直径扩大到原来的2倍,高不变,它的体积
也扩大到原来的2倍。 ( )
(3)圆柱的底面周长和高相等时,它的侧面沿高展开后
一定是正方形。 ( )
×
√
√
(教材第29页练习八第2题)
3.14×(6÷2)2×10=282.6(cm3)
282.6 cm3=282.6 mL
282.6>250
答:小萌每天喝这样一杯牛奶,有250 mL。
3.一个圆柱形玻璃杯,从里面量直径是6 cm,深10 cm。
小萌每天喝这样一杯牛奶,有250 mL吗
(教材第29页练习八第3题)
3.14×(8÷2)2×16=803.84(dm3)
803.84 dm3=803.84 L
答:这种电热水器的容积是803.84 L。
4.一种圆柱形立式电热水器的内胆直径8 dm,
高16 dm。这种电热水器的容积是多少升
(教材第29页练习八第4题)
5.一个圆柱形粮囤,从里面量得它的数据如图所示,
按每立方米稻谷重 550 kg计算,这个粮囤能装稻
谷约多少吨?
V = 3.14×22×2.5=31.4(m3)
31.4×550=17270(kg)
答:这个粮囤能装稻谷17.27吨。
17270 kg=17.27 t
(教材第29页练习八第5题)
这节课你有什么收获?
课堂小结
圆柱的体积=底面积×高
圆柱的体积=πr h
02
01
课后作业
课后练习七。
相关练习。
西师版数学六年级(下)
第3课时 圆柱的体积
圆柱和圆锥
二
1.掌握圆柱体积的计算公式,并能运用公式解决简单的实际问题。
2.理解圆柱体积计算公式的推导过程,体会转化思想在公式推导中的作用。
3.在运用公式解决问题的过程中,培养观察、猜测、分析、比较、综合的学习能力。
学习目标
【重点】
掌握圆柱体积的计算方法,并能用公式解决简单的实际问题。
【难点】
理解圆柱体积计算公式的推导过程,
体会转化思想在公式推导中的作用。
课堂导入
什么是物体的体积?
物体所占空间的大小叫做物体的体积。
你会计算下面图形的体积吗?
圆柱的体积怎样计算呢?
长方体的体积=长×宽×高
正方体的体积=棱长×棱长×棱长
长方体和正方体的体积=底面积×高
新知探究
我不会算圆柱的体积,
但会算长方体的体积。
做一做,议一议:怎样计算圆柱的体积?
如果能将圆柱变成
长方体就好了。
怎样才能把圆柱转化成长方体呢?
(教材第27页)
能不能将圆柱转化成我们学过的立体图形,计算出它的体积呢?
把圆柱的底面平均分成若干偶数份。
把圆柱切开,像这样拼起来,得到一个近似的长方体。
(教材第27页)
怎样求圆柱的体积?
观察发现:把圆柱的底面平均分成的份数越多,按照等分线沿着高切开后拼成的立体图形就越接近长方体。
(教材第27页)
把拼成的长方体与原来的圆柱比较,你能发现什么?
长方体的体积与圆柱的体积相等。
长方体的底面积等于圆柱的底面积,长方体的高等于圆柱的高。
(教材第27页)
总结圆柱体积的计算公式。
圆柱的体积= ×
长方体的体积= 底面积 × 高
V =
S
h
底面积
高
×
(教材第27页)
如果知道圆柱的底面半径r和高h,你能写出圆柱的体积公式吗?
圆柱的体积计算公式:
V =____________
πr h
(教材第27页)
圆柱的底面积是28.6 cm2,高15 cm,求圆柱的体积。
试一试
V = Sh
= 28.6×15
= 429(cm3)
答:圆柱的体积是429 cm3。
(教材第28页“试一试”)
这个圆柱的体积是多少立方厘米?
4
底面周长是31.4厘米。
圆柱高20厘米。
圆柱的底面半径:
圆柱的体积:
3.14×52×20=1570(cm3)
答:这个圆柱的体积是1570 cm3。
V=πr h
=5(cm)
(教材第28页例4)
课堂练习
(教材第29页练习八第1题)
1.计算体积。(图中单位:cm)
V=πr h
=3.14×52×6
=471(cm3)
1.计算体积。(图中单位:cm)
V=πr h
=3.14×2×12
=150.72(cm3)
(教材第29页练习八第1题)
1.计算体积。(图中单位:cm)
V=πr h
=3.14×(18.84÷3.14÷2)2×9
=254.34(cm3)
(教材第29页练习八第1题)
2.判断。(正确的在括号里画“√”,错误的画“×”。)
(1)计算圆柱形油桶能装多少升油就是求这个油桶的容
积。( )
(2)圆柱底面直径扩大到原来的2倍,高不变,它的体积
也扩大到原来的2倍。 ( )
(3)圆柱的底面周长和高相等时,它的侧面沿高展开后
一定是正方形。 ( )
×
√
√
(教材第29页练习八第2题)
3.14×(6÷2)2×10=282.6(cm3)
282.6 cm3=282.6 mL
282.6>250
答:小萌每天喝这样一杯牛奶,有250 mL。
3.一个圆柱形玻璃杯,从里面量直径是6 cm,深10 cm。
小萌每天喝这样一杯牛奶,有250 mL吗
(教材第29页练习八第3题)
3.14×(8÷2)2×16=803.84(dm3)
803.84 dm3=803.84 L
答:这种电热水器的容积是803.84 L。
4.一种圆柱形立式电热水器的内胆直径8 dm,
高16 dm。这种电热水器的容积是多少升
(教材第29页练习八第4题)
5.一个圆柱形粮囤,从里面量得它的数据如图所示,
按每立方米稻谷重 550 kg计算,这个粮囤能装稻
谷约多少吨?
V = 3.14×22×2.5=31.4(m3)
31.4×550=17270(kg)
答:这个粮囤能装稻谷17.27吨。
17270 kg=17.27 t
(教材第29页练习八第5题)
这节课你有什么收获?
课堂小结
圆柱的体积=底面积×高
圆柱的体积=πr h
02
01
课后作业
课后练习七。
相关练习。
