三 正比例和反比例 整理与复习课件数学六年级下册西师大版(共28张PPT)
文档属性
| 名称 | 三 正比例和反比例 整理与复习课件数学六年级下册西师大版(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-01 07:50:19 | ||
图片预览








文档简介
(共28张PPT)
西师版数学六年级(下)
第8课时 整理与复习
正比例和反比例
三
1.通过整理与复习,进一步掌握有关比例、正比例、反比例的知识,沟通有关知识的联系,完善认知结构。
2.能灵活运用比例知识解决一些实际问题,进一步培养数学应用意识和问题解决能力。
3.培养自主归纳、整理知识的能力。
学习目标
【重点】
整理本单元的知识,沟通知识间的内在联系。
【难点】
灵活运用正、反比例的意义,解决实际问题。
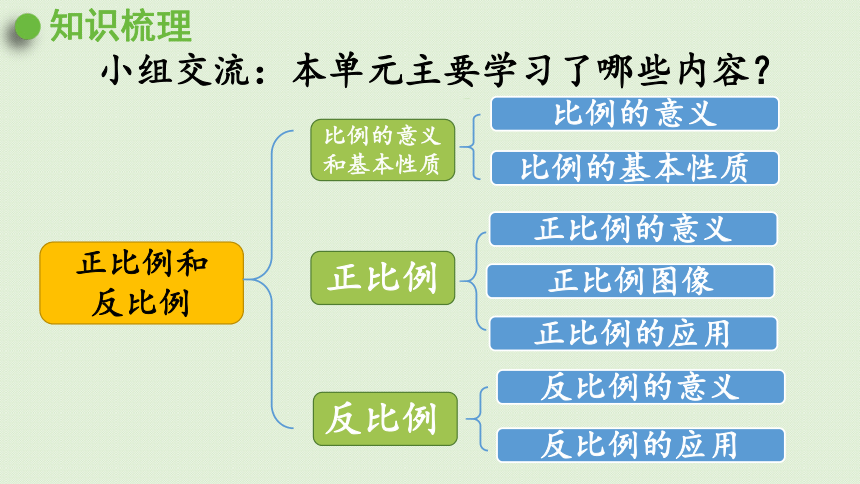
小组交流:本单元主要学习了哪些内容?
知识梳理
正比例和
反比例
比例的意义和基本性质
正比例
比例的意义
比例的基本性质
正比例的意义
正比例图像
正比例的应用
反比例
反比例的意义
反比例的应用
要点回顾
1.应用比例的定义,判断下面的比能否组成比例,把组成
的比例写下来。
知识点1:比例的意义和基本性质
比值相等的两个比才能组成比例。
6∶15和9∶10
0.5∶0.25和0.2∶0.1
6∶15和9∶10
不能组成比例
0.5∶0.25和0.2∶0.1
0.5∶0.25=0.2∶0.1
2.按要求写比例。
(1)写出两个内项都是6,两个比的比值都是5的比例。
(2)
在比例里,两个外项的积等于两个内项的积。
2.按要求写比例。
(1)写出两个内项都是6,两个比的比值都是5的比例。
(2)
30∶6=6∶1.2
知识点2:正比例和反比例的意义
3.判断下面两种量成什么比例。
(1)三角形的高一定,它的面积和底。 ( )
(2)修一段路,工作时间和工作效率。 ( )
(3)成活率一定,栽树的总棵数和成活的棵数。( )
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值(也就是商)一定,它们的关系叫做正比例关系;如果这两种量中相对应的两个数的乘积一定,它们的关系叫做反比例关系。
正比例
反比例
正比例
知识点3:正比例图像
4.一种跳绳的数量和总价如下表:
数量(根) 1 2 3 4 5 6 7
总价(元) 4 8 12 16 20 24 28
(1)在下图中描出表示数量和相对应总价的点,然后把它们连起来,再说说图像的特点。
(2)68元能买多少根跳绳
1 2 3 4 5 6 7
总价(元)
数量(根)
28
24
20
16
12
8
4
0
4.一种跳绳的数量和总价如下表:
数量(根) 1 2 3 4 5 6 7
总价(元) 4 8 12 16 20 24 28
(1)在下图中描出表示数量和相对应总价的点,然后把它们连起来,再说说图像的特点。
1 2 3 4 5 6 7
总价(元)
数量(根)
28
24
20
16
12
8
4
0
·
·
·
·
·
·
·
图像是一条直线。
解题启示
画正比例关系图像的步骤:
①认识坐标系;
②描点;
③连线。
(2)68元能买多少根跳绳
68÷4=17(根)
答:68元能买17根跳绳。
数量(根) 1 2 3 4 5 6 7
总价(元) 4 8 12 16 20 24 28
知识点4:正比例和反比例的应用
5. 3袋糖果重31.5克,现有一些这样的糖果,称得重量
是84克,这些糖果有多少袋?
根据问题中的不变量找出两种相关联的量,并正确判断这两种相关联的量成什么比例关系,并根据正、反比例关系式列出相应的方程并求解。
用正(反)比例方法解决问题的步骤
(1)分析题意,判断两种量是否成正(反)比例;
(2)再找出比例式所需的等量关系,并设所求未
知量为x;
(3)解比例。
5. 3袋糖果重31.5克,现有一些这样的糖果,称得重量
是84克,这些糖果有多少袋?
解:设这些糖果有x袋。
答:这些糖果有袋。
6.食堂有一些面粉,原计划每天用15千克,可以用5天,
在开展反对浪费活动后,实际每天用10千克,这些面
粉可以用多少天?
解:设这些面粉可以用x天。
答:这些面粉可以用7.5天。
课堂练习
1.
(教材第52页练习十四第1题)
长2.4 m,宽1.6 m
长60 cm,宽40 cm
(1)这两面国旗的长和宽的比,是否可以组成比例?
(2)如果可以组成比例,把组成的比例写出来,并指出这个比
例的内项和外项。
可以
2.4∶1.6=60∶40
内项:1.6和60
外项:2.4和40
2.大、小文具盒单价的比是4∶3,其中大文具
盒的单价是12元,小文具盒的单价是多少元?
解:设小文具盒的单价是x元。
4∶3=12∶x
x=9
答:小文具盒的单价是9元。
(教材第52页练习十四第2题)
3.
(1)学校举行方阵团体操表演,排成5列需要90人。
照这样计算,排成24列,需要多少人?
解:设需要x人。
答:需要432人。
(教材第53页练习十四第6题)
(2)学校举行方阵团体操表演,如果每列16人,
要排27列。
每列18人,要排多少列?
解:设要排x列。
27
答:要排24列。
(教材第53页练习十四第6题)
4. 张大爷至少需要准备多少千克黄豆?
我们需要做出
20千克豆浆。
0.5千克黄豆可以做2千克豆浆。
解:设张大爷至少需要准备x kg黄豆。
答:张大爷至少需要准备5 kg黄豆。
(教材第53页练习十四第7题)
5.印刷厂用一批纸装订练习本。如果每本50页,
可以装订1200本。如果每本40页,可以多装订
多少本?
解:设可以多装订x本。
1500
答:可以多装订300本。
300
(教材第53页练习十四第8题)
6. 3台打米机1时打米750 kg。照这样计算,再
增加2台同样的打米机,1时能打米多少千克?
解:设1时能打米x kg。
答:1时能打米1250 kg。
(教材第54页练习十四第13题)
7.一架飞机的飞行时间和航程如下表。
飞行时间(时) 2 3 4 6
航程(km) 1600 2400 3200 4800
(1)写出几组航程和相对应的飞行时间的比,并比较
比值的大小。说一说它们的比值表示什么。
800表示飞机的飞行速度
(教材第54页练习十四第14题)
(2)表中的航程和飞行时间成正比例吗?为什么?
成正比例。因为航程和飞行时间的比值一定。
飞行时间(时) 2 3 4 6
航程(km) 1600 2400 3200 4800
(教材第54页练习十四第14题)
(3)在下图中描出表示航程和相应飞行时间的点,然后把它们顺次连起来,并估计一下飞行2500 km要用多长时间。
1 2 3 4 5 6 7 8
航程(km)
飞行时间(时)
4800
4000
3200
2400
1600
800
0
·
·
·
·
飞行2500 km大约需要3.125时。
飞行时间(时) 2 3 4 6
航程(km) 1600 2400 3200 4800
(教材第54页练习十四第14题)
02
01
练习十四。
课后作业
相关练习。
西师版数学六年级(下)
第8课时 整理与复习
正比例和反比例
三
1.通过整理与复习,进一步掌握有关比例、正比例、反比例的知识,沟通有关知识的联系,完善认知结构。
2.能灵活运用比例知识解决一些实际问题,进一步培养数学应用意识和问题解决能力。
3.培养自主归纳、整理知识的能力。
学习目标
【重点】
整理本单元的知识,沟通知识间的内在联系。
【难点】
灵活运用正、反比例的意义,解决实际问题。
小组交流:本单元主要学习了哪些内容?
知识梳理
正比例和
反比例
比例的意义和基本性质
正比例
比例的意义
比例的基本性质
正比例的意义
正比例图像
正比例的应用
反比例
反比例的意义
反比例的应用
要点回顾
1.应用比例的定义,判断下面的比能否组成比例,把组成
的比例写下来。
知识点1:比例的意义和基本性质
比值相等的两个比才能组成比例。
6∶15和9∶10
0.5∶0.25和0.2∶0.1
6∶15和9∶10
不能组成比例
0.5∶0.25和0.2∶0.1
0.5∶0.25=0.2∶0.1
2.按要求写比例。
(1)写出两个内项都是6,两个比的比值都是5的比例。
(2)
在比例里,两个外项的积等于两个内项的积。
2.按要求写比例。
(1)写出两个内项都是6,两个比的比值都是5的比例。
(2)
30∶6=6∶1.2
知识点2:正比例和反比例的意义
3.判断下面两种量成什么比例。
(1)三角形的高一定,它的面积和底。 ( )
(2)修一段路,工作时间和工作效率。 ( )
(3)成活率一定,栽树的总棵数和成活的棵数。( )
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值(也就是商)一定,它们的关系叫做正比例关系;如果这两种量中相对应的两个数的乘积一定,它们的关系叫做反比例关系。
正比例
反比例
正比例
知识点3:正比例图像
4.一种跳绳的数量和总价如下表:
数量(根) 1 2 3 4 5 6 7
总价(元) 4 8 12 16 20 24 28
(1)在下图中描出表示数量和相对应总价的点,然后把它们连起来,再说说图像的特点。
(2)68元能买多少根跳绳
1 2 3 4 5 6 7
总价(元)
数量(根)
28
24
20
16
12
8
4
0
4.一种跳绳的数量和总价如下表:
数量(根) 1 2 3 4 5 6 7
总价(元) 4 8 12 16 20 24 28
(1)在下图中描出表示数量和相对应总价的点,然后把它们连起来,再说说图像的特点。
1 2 3 4 5 6 7
总价(元)
数量(根)
28
24
20
16
12
8
4
0
·
·
·
·
·
·
·
图像是一条直线。
解题启示
画正比例关系图像的步骤:
①认识坐标系;
②描点;
③连线。
(2)68元能买多少根跳绳
68÷4=17(根)
答:68元能买17根跳绳。
数量(根) 1 2 3 4 5 6 7
总价(元) 4 8 12 16 20 24 28
知识点4:正比例和反比例的应用
5. 3袋糖果重31.5克,现有一些这样的糖果,称得重量
是84克,这些糖果有多少袋?
根据问题中的不变量找出两种相关联的量,并正确判断这两种相关联的量成什么比例关系,并根据正、反比例关系式列出相应的方程并求解。
用正(反)比例方法解决问题的步骤
(1)分析题意,判断两种量是否成正(反)比例;
(2)再找出比例式所需的等量关系,并设所求未
知量为x;
(3)解比例。
5. 3袋糖果重31.5克,现有一些这样的糖果,称得重量
是84克,这些糖果有多少袋?
解:设这些糖果有x袋。
答:这些糖果有袋。
6.食堂有一些面粉,原计划每天用15千克,可以用5天,
在开展反对浪费活动后,实际每天用10千克,这些面
粉可以用多少天?
解:设这些面粉可以用x天。
答:这些面粉可以用7.5天。
课堂练习
1.
(教材第52页练习十四第1题)
长2.4 m,宽1.6 m
长60 cm,宽40 cm
(1)这两面国旗的长和宽的比,是否可以组成比例?
(2)如果可以组成比例,把组成的比例写出来,并指出这个比
例的内项和外项。
可以
2.4∶1.6=60∶40
内项:1.6和60
外项:2.4和40
2.大、小文具盒单价的比是4∶3,其中大文具
盒的单价是12元,小文具盒的单价是多少元?
解:设小文具盒的单价是x元。
4∶3=12∶x
x=9
答:小文具盒的单价是9元。
(教材第52页练习十四第2题)
3.
(1)学校举行方阵团体操表演,排成5列需要90人。
照这样计算,排成24列,需要多少人?
解:设需要x人。
答:需要432人。
(教材第53页练习十四第6题)
(2)学校举行方阵团体操表演,如果每列16人,
要排27列。
每列18人,要排多少列?
解:设要排x列。
27
答:要排24列。
(教材第53页练习十四第6题)
4. 张大爷至少需要准备多少千克黄豆?
我们需要做出
20千克豆浆。
0.5千克黄豆可以做2千克豆浆。
解:设张大爷至少需要准备x kg黄豆。
答:张大爷至少需要准备5 kg黄豆。
(教材第53页练习十四第7题)
5.印刷厂用一批纸装订练习本。如果每本50页,
可以装订1200本。如果每本40页,可以多装订
多少本?
解:设可以多装订x本。
1500
答:可以多装订300本。
300
(教材第53页练习十四第8题)
6. 3台打米机1时打米750 kg。照这样计算,再
增加2台同样的打米机,1时能打米多少千克?
解:设1时能打米x kg。
答:1时能打米1250 kg。
(教材第54页练习十四第13题)
7.一架飞机的飞行时间和航程如下表。
飞行时间(时) 2 3 4 6
航程(km) 1600 2400 3200 4800
(1)写出几组航程和相对应的飞行时间的比,并比较
比值的大小。说一说它们的比值表示什么。
800表示飞机的飞行速度
(教材第54页练习十四第14题)
(2)表中的航程和飞行时间成正比例吗?为什么?
成正比例。因为航程和飞行时间的比值一定。
飞行时间(时) 2 3 4 6
航程(km) 1600 2400 3200 4800
(教材第54页练习十四第14题)
(3)在下图中描出表示航程和相应飞行时间的点,然后把它们顺次连起来,并估计一下飞行2500 km要用多长时间。
1 2 3 4 5 6 7 8
航程(km)
飞行时间(时)
4800
4000
3200
2400
1600
800
0
·
·
·
·
飞行2500 km大约需要3.125时。
飞行时间(时) 2 3 4 6
航程(km) 1600 2400 3200 4800
(教材第54页练习十四第14题)
02
01
练习十四。
课后作业
相关练习。
