3.6 反比例的意义课件 数学 六年级下册西师大版(共29张PPT)
文档属性
| 名称 | 3.6 反比例的意义课件 数学 六年级下册西师大版(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-01 07:52:49 | ||
图片预览







文档简介
(共29张PPT)
西师版数学六年级(下)
第6课时 反比例的意义
正比例和反比例
三
1.能够结合具体情境认识成反比例的量,理解反比例关系,能判断两种量是否成反比例关系。
2.经历反比例关系有关知识的构建过程,培养归纳概括能力,感悟函数与对应的思想。
3.感受事物充满了运动与变化,渗透辩证唯物主义思想。
学习目标
【重点】
正确理解反比例的意义。
【难点】
正确判断两种量是否成反比例关系.。
课堂导入
面包总价与数量之间有什么关系呢?为什么?
1.面包单价为2元。
数量(个)
总价(元)
1
2
2
4
3
6
4
8
5
10
6
14
7
12
8
16
…
…
正比例关系
两种相关联的量的比值(商)一定。
2.面包店有以下单价的面包,小明有30元,可以买同
种面包多少个 请填写表格。
单价(元)
数量(个)
1
30
2
15
3
10
5
6
10
3
…
…
单价增加,购买的数量随着减少。
总价不变。
单价和数量成正比例吗?
那是什么关系呢?
通过表格,你发现了什么?
探究新知
1
60名游客在井冈山游览,准备分组活动,提出的分组建议如下表。
(教材第48页例1)
每组人数(人) 3 5 6 10
组数(组) 20 12 10 4
从表中你发现了什么规律?根据这种规律把上表填写完整。
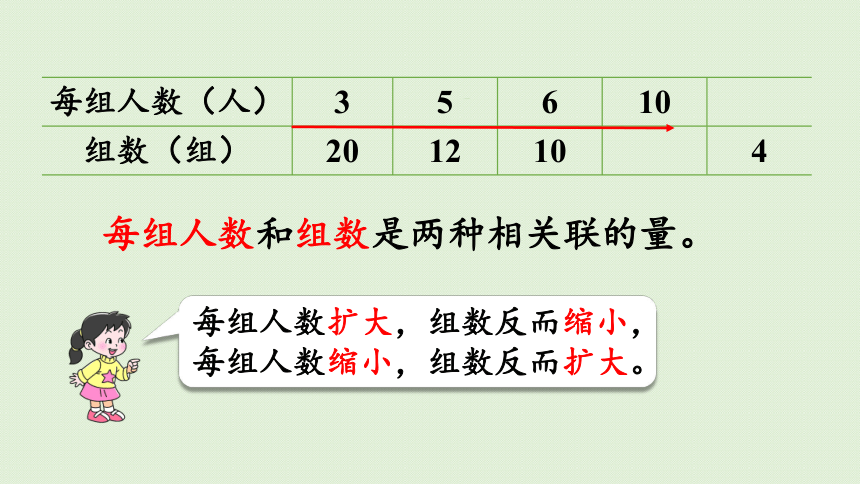
每组人数(人) 3 5 6 10
组数(组) 20 12 10 4
每组人数和组数是两种相关联的量。
每组人数扩大,组数反而缩小,每组人数缩小,组数反而扩大。
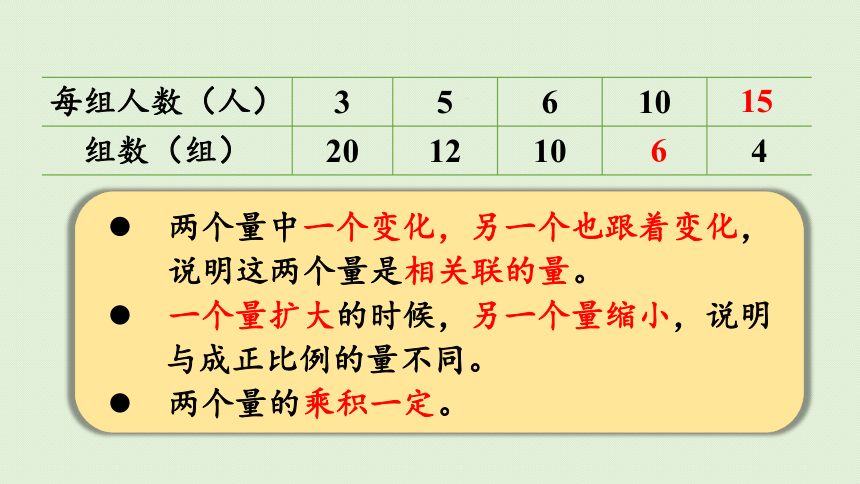
每组人数(人) 3 5 6 10
组数(组) 20 12 10 4
15
6
=60
×
=60
×
=60
×
每组人数×组数=游客总人数(积一定)
每组人数和组数的乘积是一定的。
两个量中一个变化,另一个也跟着变化,
说明这两个量是相关联的量。
一个量扩大的时候,另一个量缩小,说明
与成正比例的量不同。
两个量的乘积一定。
每组人数(人) 3 5 6 10
组数(组) 20 12 10 4
15
6
探索规律,并按规律填表。
试一试
这篇稿子,如果每分打120 个字,25分可以打完。
每分钟打字个数(个) 120 100 75 60
所需时间(分) 25 30 60
每分钟打字个数和所需时间是两种相关联的量。
每分钟打字个数增多,所需时间反而缩短,每分钟打字个数减少,所需时间反而增加。
每分钟打字个数(个) 120 100 75 60
所需时间(分) 25 30 60
每分钟打字个数(个) 120 100 75 60
所需时间(分) 25 30 60
=3000
×
=3000
×
每分钟打字个数×所需时间=稿子总字数(积一定)
每分钟打字个数和所需时间的乘积是一定的。
40
50
50
从上面的两个例子中,你发现了什么?
议一议
在每组人数和组数这两种相关联的量中,相对应的两个数的乘积是一定的。
在每分打字个数和打字时间两种相关联的量中,相对应的两个数的乘积也是一定的。
像这样的两种量,叫做成反比例的量,它们的关系叫做反比例关系。
两种量成反比例关系要满足的三个条件
(1)必须是两种相关联的量。
(2)一种量变化,另一种量也随着变化。
(3)两种量中相对应的两个数的积一定。
今天所学的反比例与之前学的正比例相比较,有什么相同点和不同点?
正比例 反比例
相同点 不同点
都有两种相关联的量,且都有一个定量。
两种相关联的量同时扩大或缩小,而且相对应的两个数的比值(商)一定。
两种相关联的量一个扩大一个缩小,且相对应的两个数的积是一定的。
生活中还有哪些成反比例的量?
议一议
如果总价一定,单价与数量成反比例关系。
如果长方形的面积一定,长与宽成反比例关系。
用24个边长为1 dm的正方形拼1个长方形,把所拼成的长方形的长和宽填入下面的表格里。
(教材第49页课堂活动第1题)
长(dm)
宽(dm)
在上表中,长和宽成反比例吗?为什么?
1
24
2
12
3
8
4
6
成反比例。长和宽的积是一定的。
课
堂
活
动
用橡皮筋在钉子板上围几个宽为2 cm的长方形,把围成的长方形的长和面积填入下面的表格里。
长(cm)
宽(cm) 2 2 2 2
面积(cm2)
在上表中,长和面积成比例吗?成什么比例?
1
2
2
4
3
6
4
8
长方形的宽一定,长和面积成正比例。
(教材第49页课堂活动第2题)
用硬纸片做几个周长为 30 cm的长方形,将所做的长方形的长和宽填入下表。
(教材第50页课堂活动第3题)
长(cm) 10
宽(cm) 5
在上表中,长和宽成比例吗?为什么?
9
6
8
7
11
4
虽然当长方形的周长一定时,长随宽的变化而变化,且它们的和是一定,但它们的积和商都不一定,故长和宽不成比例。
课堂练习
1.下面各表中的两种量成反比例吗?为什么
(教材第50页练习十三第1题)
每天的烧煤量(kg) 20 40 50 100
烧的天数(天) 50 25 20 10
成反比例。因为煤的总量一定,即每天的烧煤量与烧的天数的乘积一定。
(1)
成反比例。因为平行四边形的面积一定,即平行四边形的底与高的乘积一定。
平行四边形的底(cm) 20 15 10 6
平行四边形的高(cm) 3 4 6 10
(2)
(教材第50页练习十三第1题)
(1)表中有哪两种量?它们是不是相关联的量?
表中有每天运的吨数和需要的天数两种量。它们是相关联的量。
2.运一批货物,每天运的吨数和需要的天数如下表。
根据表回答下面的问题。
每天运的吨数 300 150 100 75 60 50
需要的天数 1 2 3 4 5 6
(2)写出几组这两种量中相对应的两个数的积,并比
较积的大小。
300 ×1 =300
150 × 2=300
100 × 3=300
75 ×4 =300
60 × 5=300
50 × 6=300
积相等
每天运的吨数 300 150 100 75 60 50
需要的天数 1 2 3 4 5 6
2.运一批货物,每天运的吨数和需要的天数如下表。
根据表回答下面的问题。
(3)说明这个积所表示的意义。
这个积表示的意义是这批货物的总吨数。
每天运的吨数 300 150 100 75 60 50
需要的天数 1 2 3 4 5 6
2.运一批货物,每天运的吨数和需要的天数如下表。
根据表回答下面的问题。
(4)表中相关联的两种量成反比例吗?为什么?
每天运的吨数和需要的天数是两种相关联的量。
每天运的吨数×需要的天数=货物总吨数(一定)
每天运的吨数和需要的天数成反比例。
每天运的吨数 300 150 100 75 60 50
需要的天数 1 2 3 4 5 6
2.运一批货物,每天运的吨数和需要的天数如下表。
根据表回答下面的问题。
课堂小结
这节课你有什么收获?
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中,相对应的两个数的乘积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
反比例的意义:
(1)两种量是相关联的量。
(2)两种量的乘积一定。
3.判断两种量成什么比例的关键:
商一定,还是积一定。
这节课你有什么收获?
02
01
课后作业
练习十三。
相关练习。
西师版数学六年级(下)
第6课时 反比例的意义
正比例和反比例
三
1.能够结合具体情境认识成反比例的量,理解反比例关系,能判断两种量是否成反比例关系。
2.经历反比例关系有关知识的构建过程,培养归纳概括能力,感悟函数与对应的思想。
3.感受事物充满了运动与变化,渗透辩证唯物主义思想。
学习目标
【重点】
正确理解反比例的意义。
【难点】
正确判断两种量是否成反比例关系.。
课堂导入
面包总价与数量之间有什么关系呢?为什么?
1.面包单价为2元。
数量(个)
总价(元)
1
2
2
4
3
6
4
8
5
10
6
14
7
12
8
16
…
…
正比例关系
两种相关联的量的比值(商)一定。
2.面包店有以下单价的面包,小明有30元,可以买同
种面包多少个 请填写表格。
单价(元)
数量(个)
1
30
2
15
3
10
5
6
10
3
…
…
单价增加,购买的数量随着减少。
总价不变。
单价和数量成正比例吗?
那是什么关系呢?
通过表格,你发现了什么?
探究新知
1
60名游客在井冈山游览,准备分组活动,提出的分组建议如下表。
(教材第48页例1)
每组人数(人) 3 5 6 10
组数(组) 20 12 10 4
从表中你发现了什么规律?根据这种规律把上表填写完整。
每组人数(人) 3 5 6 10
组数(组) 20 12 10 4
每组人数和组数是两种相关联的量。
每组人数扩大,组数反而缩小,每组人数缩小,组数反而扩大。
每组人数(人) 3 5 6 10
组数(组) 20 12 10 4
15
6
=60
×
=60
×
=60
×
每组人数×组数=游客总人数(积一定)
每组人数和组数的乘积是一定的。
两个量中一个变化,另一个也跟着变化,
说明这两个量是相关联的量。
一个量扩大的时候,另一个量缩小,说明
与成正比例的量不同。
两个量的乘积一定。
每组人数(人) 3 5 6 10
组数(组) 20 12 10 4
15
6
探索规律,并按规律填表。
试一试
这篇稿子,如果每分打120 个字,25分可以打完。
每分钟打字个数(个) 120 100 75 60
所需时间(分) 25 30 60
每分钟打字个数和所需时间是两种相关联的量。
每分钟打字个数增多,所需时间反而缩短,每分钟打字个数减少,所需时间反而增加。
每分钟打字个数(个) 120 100 75 60
所需时间(分) 25 30 60
每分钟打字个数(个) 120 100 75 60
所需时间(分) 25 30 60
=3000
×
=3000
×
每分钟打字个数×所需时间=稿子总字数(积一定)
每分钟打字个数和所需时间的乘积是一定的。
40
50
50
从上面的两个例子中,你发现了什么?
议一议
在每组人数和组数这两种相关联的量中,相对应的两个数的乘积是一定的。
在每分打字个数和打字时间两种相关联的量中,相对应的两个数的乘积也是一定的。
像这样的两种量,叫做成反比例的量,它们的关系叫做反比例关系。
两种量成反比例关系要满足的三个条件
(1)必须是两种相关联的量。
(2)一种量变化,另一种量也随着变化。
(3)两种量中相对应的两个数的积一定。
今天所学的反比例与之前学的正比例相比较,有什么相同点和不同点?
正比例 反比例
相同点 不同点
都有两种相关联的量,且都有一个定量。
两种相关联的量同时扩大或缩小,而且相对应的两个数的比值(商)一定。
两种相关联的量一个扩大一个缩小,且相对应的两个数的积是一定的。
生活中还有哪些成反比例的量?
议一议
如果总价一定,单价与数量成反比例关系。
如果长方形的面积一定,长与宽成反比例关系。
用24个边长为1 dm的正方形拼1个长方形,把所拼成的长方形的长和宽填入下面的表格里。
(教材第49页课堂活动第1题)
长(dm)
宽(dm)
在上表中,长和宽成反比例吗?为什么?
1
24
2
12
3
8
4
6
成反比例。长和宽的积是一定的。
课
堂
活
动
用橡皮筋在钉子板上围几个宽为2 cm的长方形,把围成的长方形的长和面积填入下面的表格里。
长(cm)
宽(cm) 2 2 2 2
面积(cm2)
在上表中,长和面积成比例吗?成什么比例?
1
2
2
4
3
6
4
8
长方形的宽一定,长和面积成正比例。
(教材第49页课堂活动第2题)
用硬纸片做几个周长为 30 cm的长方形,将所做的长方形的长和宽填入下表。
(教材第50页课堂活动第3题)
长(cm) 10
宽(cm) 5
在上表中,长和宽成比例吗?为什么?
9
6
8
7
11
4
虽然当长方形的周长一定时,长随宽的变化而变化,且它们的和是一定,但它们的积和商都不一定,故长和宽不成比例。
课堂练习
1.下面各表中的两种量成反比例吗?为什么
(教材第50页练习十三第1题)
每天的烧煤量(kg) 20 40 50 100
烧的天数(天) 50 25 20 10
成反比例。因为煤的总量一定,即每天的烧煤量与烧的天数的乘积一定。
(1)
成反比例。因为平行四边形的面积一定,即平行四边形的底与高的乘积一定。
平行四边形的底(cm) 20 15 10 6
平行四边形的高(cm) 3 4 6 10
(2)
(教材第50页练习十三第1题)
(1)表中有哪两种量?它们是不是相关联的量?
表中有每天运的吨数和需要的天数两种量。它们是相关联的量。
2.运一批货物,每天运的吨数和需要的天数如下表。
根据表回答下面的问题。
每天运的吨数 300 150 100 75 60 50
需要的天数 1 2 3 4 5 6
(2)写出几组这两种量中相对应的两个数的积,并比
较积的大小。
300 ×1 =300
150 × 2=300
100 × 3=300
75 ×4 =300
60 × 5=300
50 × 6=300
积相等
每天运的吨数 300 150 100 75 60 50
需要的天数 1 2 3 4 5 6
2.运一批货物,每天运的吨数和需要的天数如下表。
根据表回答下面的问题。
(3)说明这个积所表示的意义。
这个积表示的意义是这批货物的总吨数。
每天运的吨数 300 150 100 75 60 50
需要的天数 1 2 3 4 5 6
2.运一批货物,每天运的吨数和需要的天数如下表。
根据表回答下面的问题。
(4)表中相关联的两种量成反比例吗?为什么?
每天运的吨数和需要的天数是两种相关联的量。
每天运的吨数×需要的天数=货物总吨数(一定)
每天运的吨数和需要的天数成反比例。
每天运的吨数 300 150 100 75 60 50
需要的天数 1 2 3 4 5 6
2.运一批货物,每天运的吨数和需要的天数如下表。
根据表回答下面的问题。
课堂小结
这节课你有什么收获?
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中,相对应的两个数的乘积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
反比例的意义:
(1)两种量是相关联的量。
(2)两种量的乘积一定。
3.判断两种量成什么比例的关键:
商一定,还是积一定。
这节课你有什么收获?
02
01
课后作业
练习十三。
相关练习。
