二 圆柱和圆锥 整理与复习(课件) 数学六年级下册 西师大版(共22张PPT)
文档属性
| 名称 | 二 圆柱和圆锥 整理与复习(课件) 数学六年级下册 西师大版(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-01 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
西师版数学六年级(下)
第7课时 整理与复习
圆柱和圆锥
二
1.通过自主整理,进一步促进对有关圆柱、圆锥知识的掌握,沟通圆柱、圆锥等有关知识的联系。
2.进一步培养应用圆柱、圆锥的知识来解决问题的能力,发展空间概念。
3.在整理与复习的过程中培养自主整理复习的学习方法和能力。
学习目标
【重点】
巩固圆柱表面积的计算方法以及圆柱、圆锥体积的计算公式。
【难点】
把握圆柱与圆锥的联系与区别,明确相关概念,灵活地运用计算公式解决实际问题。
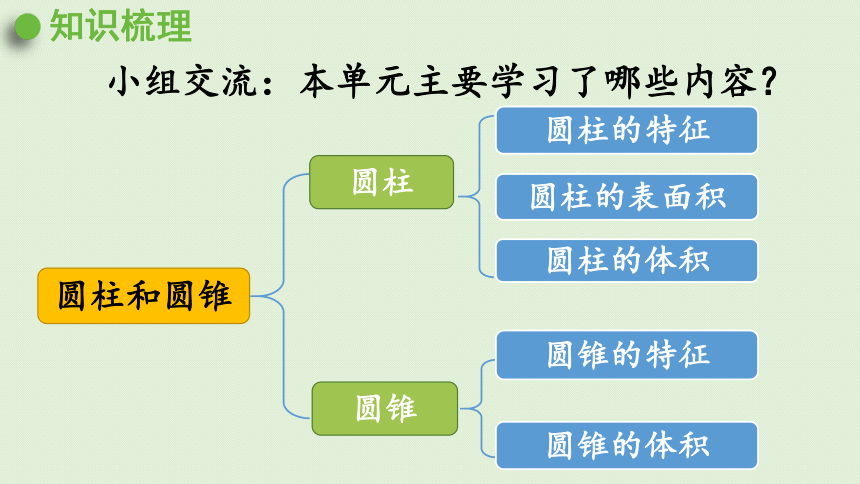
小组交流:本单元主要学习了哪些内容?
知识梳理
圆柱和圆锥
圆柱
圆锥
圆柱的特征
圆柱的表面积
圆锥的特征
圆锥的体积
圆柱的体积
要点回顾
1.填空题。
知识点1:圆柱的特征
(1)圆柱的上、下两个底面都是( ),它们的
面积( )。
(2)圆柱的侧面沿高展开是长方形,长方形的长是
圆柱的( ),宽是圆柱的( )。
(3)圆柱有( )条高。
圆
相等
高
底面周长
无数
知识点2:圆柱的表面积
2.计算下面图形的表面积。
圆柱的侧面积=底面周长×高
圆柱的表面积=圆柱的侧面积+两个底面的面积
高8 dm
直径4 dm
3.14×(4÷2) =12.56(dm )
3.14×4×8=100.48(dm )
12.56×2+100.48=125.6(dm )
知识点3:圆柱的体积
3.一块正方形木料,它的棱长是4 dm。把这块木料加
工成一个最大的圆柱。这个圆柱的体积是多少?
圆柱的体积=底面积×高 圆柱的体积=πr h
答:这个圆柱的体积是50.24 dm3 。
圆柱的底面直径和高都是4 dm。
3.14×(4÷2) ×4=50.24(dm3)
知识点4:圆锥的体积
4.蚁狮用来捕食的洞穴是个倒圆锥形。蚁狮挖了一个洞
口直径约4.2厘米、深2厘米的倒圆锥形洞穴,大约需
要挖多少立方厘米的土
×3.14×(4.2÷2)2×2
= 9.2316(cm3)
答:大约需要挖9.2316 cm3的土。
圆锥的体积= ×底面积×高
知识点5:解决问题
5.一种水稻磨米机的漏斗是由圆柱和圆锥两部分组成。
底面直径是4 dm,圆柱高2 dm。圆锥高4.2 dm。每
立方分米稻谷重0.65 kg。
(1)这个漏斗最多能装多少千克稻谷?(得数保留两
位小数。)
先求这个漏斗的体积
每立方分米稻谷质量
×
圆锥的体积
圆柱的体积
3.14×(4÷2)2×4.2×
3.14×(4÷2)2×2
+
+
( )×0.65
3.14×(4÷2)2×4.2×
3.14×(4÷2)2×2
+
=(17.584+25.12)×0.65
≈ 27.76(kg)
答:这个漏斗最多能装27.76 kg稻谷。
(2)如果稻谷的出米率是70%,那么一漏斗稻谷能磨
多少千克大米?
出米率 = 磨出米的质量÷稻谷的质量
?
磨出米的质量 = 稻谷的质量×出米率
27.76×70% = 19.432(kg)
答:一漏斗稻谷能磨19.432 kg大米。
5.一种水稻磨米机的漏斗是由圆柱和圆锥两部分组成。
底面直径是4 dm,圆柱高2 dm。圆锥高4.2 dm。每
立方分米稻谷重0.65 kg。
解题启示
在思考分析过程中把圆柱、圆锥体积的意义和实际问题情境意义相对应,从而确定解决问题的方法。
课堂练习
1.一个圆柱的底面半径是3 cm,高是20 cm。这个
圆柱的表面积是多少平方厘米 它的体积是多少
立方厘米
表面积:2×3.14×3×20+3.14×32×2=433.32(cm2)
体积:3.14×32×20=565.2(cm3)
答:这个圆柱的表面积是433.32 cm2 ,它的体积是565.2 cm3 。
(教材第36页练习十第2题)
900×40%÷6=60(mL)
答:每个小杯装水60 mL。
2.一个水壶装有900 mL水,倒出壶中40%的水,
刚好装满容积相同的6个小杯。每个小杯装
水多少毫升
(教材第36页练习十第3题)
3.滨城小学修建综合楼,要在深4 m,直径0.8 m
的圆柱形地基孔中浇灌混凝土。16 个这样的地
基孔共需浇灌混凝土多少立方米?
3.14×(0.8÷2)2×4=2.0096(m3)
2.0096×16=32.1536(m3)
答:16个这样的地基孔共需浇灌混凝土32.1536 m3。
(教材第36页练习十第4题)
4.有关资料显示,每人每日正常饮水量约为1 L。小
红的水杯是圆柱形的,它的内直径是4 cm,深是
10 cm,她每天需要喝几杯水 (得数保留整数。)
1 L=1000 mL
3.14×(4÷2)2×10=125.6(cm3)
125.6 cm3=125.6 mL
1000÷125.6≈8(杯)
答:她每天需要喝8杯水。
(教材第37页练习十第5题)
5.计算这个陀螺的体积。(图中单位:cm)
(教材第37页练习十第6题)
r=2 cm
V圆柱= S底h=12.56×3=37.68(cm3)
S底= 3.14×22=12.56(cm2)
V圆锥=S底h=12.56(cm3)
V陀螺=V圆柱+V圆锥=50.24(cm3)
答:这个陀螺的体积是50.24 cm3。
(教材第37页练习十第6题)
(教材第37页练习十第7题)
6.压路机前轮转动一周,可以压路多少平方米?
如果平均每分前进50 m,这台压路机 1 时能
压路多少平方米?
这台压路机前轮直径1.2米,宽1.8米。
这台压路机前轮直径1.2米,宽1.8米。
转动一周就是求圆柱的侧面积:
S侧=3.14×1.2×1.8=6.7824(m2)
1时前进:50×60=3000(m)
1时压路:3000×1.8=5400(m2)
答:转动一周可以压路6.7824 m2,这台压路机1时
能压路5400 m2。
(教材第37页练习十第7题)
(教材第37页练习十第9题)
7.游乐中心内一个长方形儿童游泳池,长25 m,宽
12.56 m,深1.2 m。如果用直径20 cm的进水管向游
泳池里注水,水流速度按每分100 m计算,注满一池
水要多长时间
20 cm=0.2 m
25×12.56×1.2=376.8(m3)
376.8÷3.14=120(分)
3.14×(0.2÷2)2×100=3.14(m3)
答:注满一池水要120分。
02
01
练习十。
课后作业
相关练习。
西师版数学六年级(下)
第7课时 整理与复习
圆柱和圆锥
二
1.通过自主整理,进一步促进对有关圆柱、圆锥知识的掌握,沟通圆柱、圆锥等有关知识的联系。
2.进一步培养应用圆柱、圆锥的知识来解决问题的能力,发展空间概念。
3.在整理与复习的过程中培养自主整理复习的学习方法和能力。
学习目标
【重点】
巩固圆柱表面积的计算方法以及圆柱、圆锥体积的计算公式。
【难点】
把握圆柱与圆锥的联系与区别,明确相关概念,灵活地运用计算公式解决实际问题。
小组交流:本单元主要学习了哪些内容?
知识梳理
圆柱和圆锥
圆柱
圆锥
圆柱的特征
圆柱的表面积
圆锥的特征
圆锥的体积
圆柱的体积
要点回顾
1.填空题。
知识点1:圆柱的特征
(1)圆柱的上、下两个底面都是( ),它们的
面积( )。
(2)圆柱的侧面沿高展开是长方形,长方形的长是
圆柱的( ),宽是圆柱的( )。
(3)圆柱有( )条高。
圆
相等
高
底面周长
无数
知识点2:圆柱的表面积
2.计算下面图形的表面积。
圆柱的侧面积=底面周长×高
圆柱的表面积=圆柱的侧面积+两个底面的面积
高8 dm
直径4 dm
3.14×(4÷2) =12.56(dm )
3.14×4×8=100.48(dm )
12.56×2+100.48=125.6(dm )
知识点3:圆柱的体积
3.一块正方形木料,它的棱长是4 dm。把这块木料加
工成一个最大的圆柱。这个圆柱的体积是多少?
圆柱的体积=底面积×高 圆柱的体积=πr h
答:这个圆柱的体积是50.24 dm3 。
圆柱的底面直径和高都是4 dm。
3.14×(4÷2) ×4=50.24(dm3)
知识点4:圆锥的体积
4.蚁狮用来捕食的洞穴是个倒圆锥形。蚁狮挖了一个洞
口直径约4.2厘米、深2厘米的倒圆锥形洞穴,大约需
要挖多少立方厘米的土
×3.14×(4.2÷2)2×2
= 9.2316(cm3)
答:大约需要挖9.2316 cm3的土。
圆锥的体积= ×底面积×高
知识点5:解决问题
5.一种水稻磨米机的漏斗是由圆柱和圆锥两部分组成。
底面直径是4 dm,圆柱高2 dm。圆锥高4.2 dm。每
立方分米稻谷重0.65 kg。
(1)这个漏斗最多能装多少千克稻谷?(得数保留两
位小数。)
先求这个漏斗的体积
每立方分米稻谷质量
×
圆锥的体积
圆柱的体积
3.14×(4÷2)2×4.2×
3.14×(4÷2)2×2
+
+
( )×0.65
3.14×(4÷2)2×4.2×
3.14×(4÷2)2×2
+
=(17.584+25.12)×0.65
≈ 27.76(kg)
答:这个漏斗最多能装27.76 kg稻谷。
(2)如果稻谷的出米率是70%,那么一漏斗稻谷能磨
多少千克大米?
出米率 = 磨出米的质量÷稻谷的质量
?
磨出米的质量 = 稻谷的质量×出米率
27.76×70% = 19.432(kg)
答:一漏斗稻谷能磨19.432 kg大米。
5.一种水稻磨米机的漏斗是由圆柱和圆锥两部分组成。
底面直径是4 dm,圆柱高2 dm。圆锥高4.2 dm。每
立方分米稻谷重0.65 kg。
解题启示
在思考分析过程中把圆柱、圆锥体积的意义和实际问题情境意义相对应,从而确定解决问题的方法。
课堂练习
1.一个圆柱的底面半径是3 cm,高是20 cm。这个
圆柱的表面积是多少平方厘米 它的体积是多少
立方厘米
表面积:2×3.14×3×20+3.14×32×2=433.32(cm2)
体积:3.14×32×20=565.2(cm3)
答:这个圆柱的表面积是433.32 cm2 ,它的体积是565.2 cm3 。
(教材第36页练习十第2题)
900×40%÷6=60(mL)
答:每个小杯装水60 mL。
2.一个水壶装有900 mL水,倒出壶中40%的水,
刚好装满容积相同的6个小杯。每个小杯装
水多少毫升
(教材第36页练习十第3题)
3.滨城小学修建综合楼,要在深4 m,直径0.8 m
的圆柱形地基孔中浇灌混凝土。16 个这样的地
基孔共需浇灌混凝土多少立方米?
3.14×(0.8÷2)2×4=2.0096(m3)
2.0096×16=32.1536(m3)
答:16个这样的地基孔共需浇灌混凝土32.1536 m3。
(教材第36页练习十第4题)
4.有关资料显示,每人每日正常饮水量约为1 L。小
红的水杯是圆柱形的,它的内直径是4 cm,深是
10 cm,她每天需要喝几杯水 (得数保留整数。)
1 L=1000 mL
3.14×(4÷2)2×10=125.6(cm3)
125.6 cm3=125.6 mL
1000÷125.6≈8(杯)
答:她每天需要喝8杯水。
(教材第37页练习十第5题)
5.计算这个陀螺的体积。(图中单位:cm)
(教材第37页练习十第6题)
r=2 cm
V圆柱= S底h=12.56×3=37.68(cm3)
S底= 3.14×22=12.56(cm2)
V圆锥=S底h=12.56(cm3)
V陀螺=V圆柱+V圆锥=50.24(cm3)
答:这个陀螺的体积是50.24 cm3。
(教材第37页练习十第6题)
(教材第37页练习十第7题)
6.压路机前轮转动一周,可以压路多少平方米?
如果平均每分前进50 m,这台压路机 1 时能
压路多少平方米?
这台压路机前轮直径1.2米,宽1.8米。
这台压路机前轮直径1.2米,宽1.8米。
转动一周就是求圆柱的侧面积:
S侧=3.14×1.2×1.8=6.7824(m2)
1时前进:50×60=3000(m)
1时压路:3000×1.8=5400(m2)
答:转动一周可以压路6.7824 m2,这台压路机1时
能压路5400 m2。
(教材第37页练习十第7题)
(教材第37页练习十第9题)
7.游乐中心内一个长方形儿童游泳池,长25 m,宽
12.56 m,深1.2 m。如果用直径20 cm的进水管向游
泳池里注水,水流速度按每分100 m计算,注满一池
水要多长时间
20 cm=0.2 m
25×12.56×1.2=376.8(m3)
376.8÷3.14=120(分)
3.14×(0.2÷2)2×100=3.14(m3)
答:注满一池水要120分。
02
01
练习十。
课后作业
相关练习。
