西师大版数学六年级下册总复习 平面图形的认识 课件(共38张PPT)
文档属性
| 名称 | 西师大版数学六年级下册总复习 平面图形的认识 课件(共38张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-01 00:00:00 | ||
图片预览





文档简介
(共38张PPT)
第8课时 平面图形的认识
总复习
五
西师版数学六年级(下)
1.回顾并牢固掌握平面图形的基本特征,明确概念间的区别和联系。
2.把握平面图形间的相互联系,进行完整的知识建构,培养空间观念。
3.在整理复习中运用分类整理的方法,培养对比分析、归纳整理的能力,在小组活动中培养学生合作学习的能力。
学习目标
【重点】
能对平面图形进行分类,掌握直线、射线和线段的
联系和区别。
【难点】
角的度量和平行线的画法。
知识梳理
想一想,我们都学过哪些平面图形?
平面图形
不封闭图形
封闭图形
不封闭图形
直线、 射线 、线段
角
平行线 相交线
封闭图形
长方形
正方形
平行四边形
三角形
梯形
圆
四边形
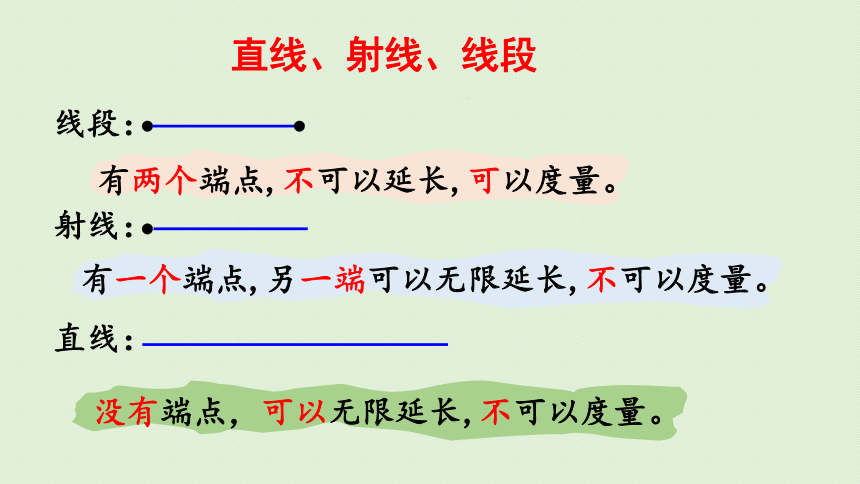
直线、射线、线段
●
●
●
线段:
射线:
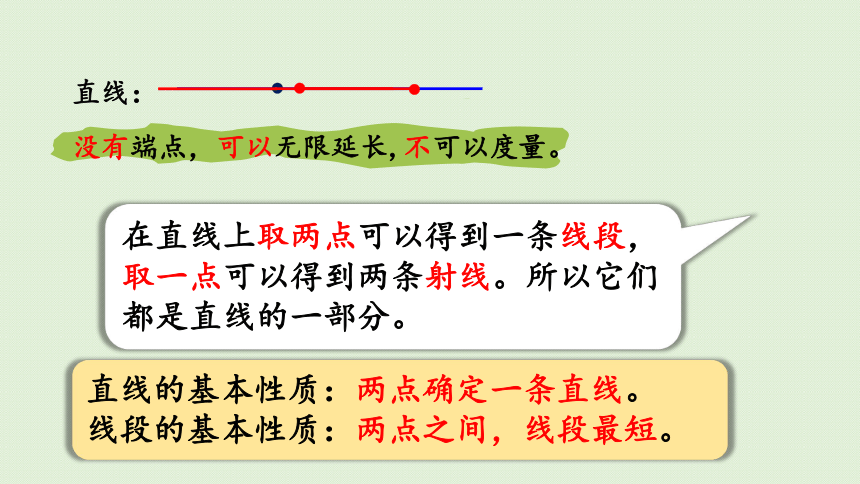
直线:
有两个端点,不可以延长,可以度量。
有一个端点,另一端可以无限延长,不可以度量。
没有端点,可以无限延长,不可以度量。
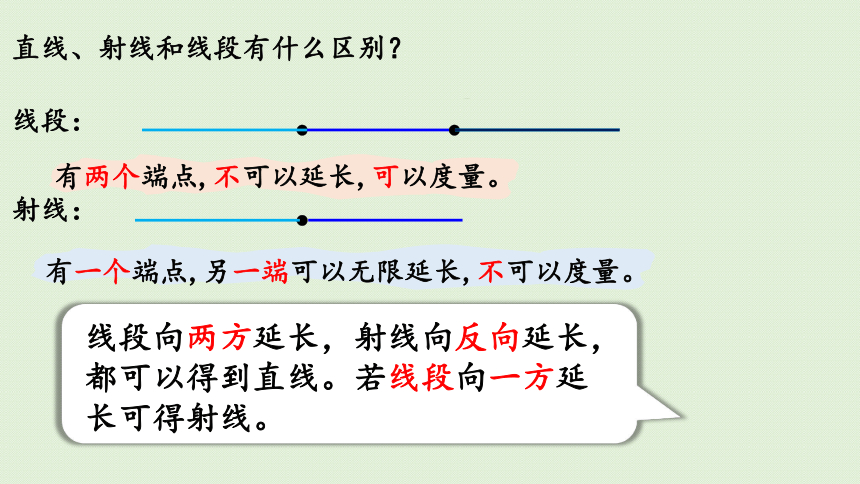
直线、射线和线段有什么区别?
●
●
●
线段:
射线:
有两个端点,不可以延长,可以度量。
有一个端点,另一端可以无限延长,不可以度量。
线段向两方延长,射线向反向延长,
都可以得到直线。若线段向一方延
长可得射线。
没有端点,可以无限延长,不可以度量。
●
●
●
在直线上取两点可以得到一条线段,取一点可以得到两条射线。所以它们都是直线的一部分。
直线的基本性质:两点确定一条直线。
线段的基本性质:两点之间,线段最短。
直线:
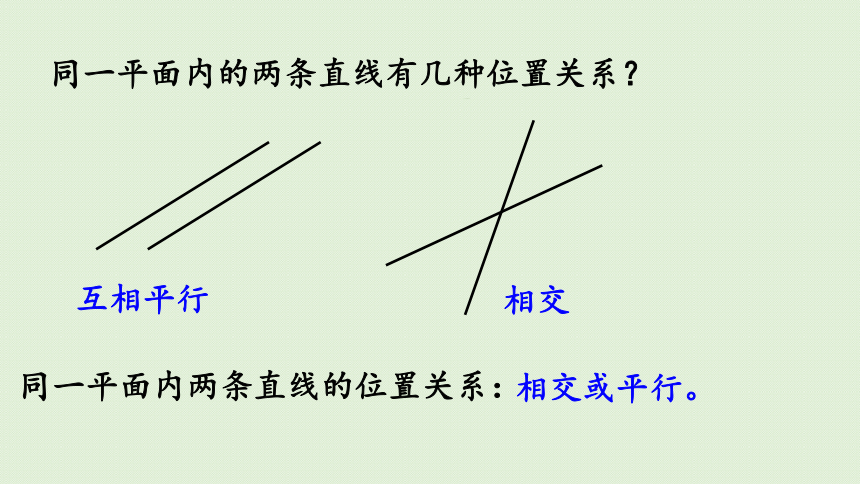
同一平面内的两条直线有几种位置关系?
互相平行
同一平面内两条直线的位置关系:
相交
相交或平行。
角
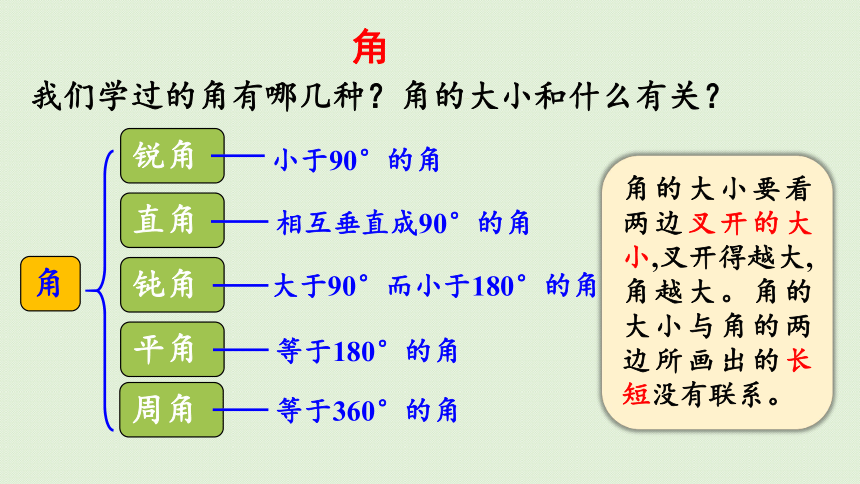
我们学过的角有哪几种?角的大小和什么有关?
两条直线
平行
相交
平行线
角
角
我们学过的角有哪几种?角的大小和什么有关?
角
锐角
直角
钝角
平角
周角
相互垂直成90°的角
小于90°的角
大于90°而小于180°的角
等于180°的角
等于360°的角
角的大小要看两边叉开的大小,叉开得越大,角越大。角的大小与角的两边所画出的长短没有联系。
封闭图形
三角形
多边形
圆
四边形
由曲线围成的封闭图形
三角形、四边形、圆
三角形
锐角三角形
直角三角形
钝角三角形
按角分
不等边三角形
等腰三角形
按边分
等边三角形
等腰三角形
三角形
等边三角形
三角形、四边形、圆
四边形
不规则四边形
平行四边形
三角形、四边形、圆
梯形
等腰梯形
一般梯形
四个角都
是直角
长方形
四个边
都相等
正方形
直角梯形
三角形
高
底
高
下底
上底
底
高
平行四边形
梯形
三角形有三条高。
平行四边形有两组对边平行且相等 平行线间的距离处处相等,即平行线间任何一条距离都是高。它有无数高。
梯形有一组对
边平行,有无
数高。
三角形内角和是180°。
O
r
d
圆内有无数条半径和直径,同一圆内直径等于半径的2倍。
连接圆心和圆上任意一点的线段叫做圆的半径, 通过圆心且两个端点都在圆周上的线段叫做圆的直径。 所有直径和半径都相等。
圆心决定圆的位置,半径决定圆的大小。圆是轴对称图形,有无数条对称轴。
要点回顾
1.按要求画图。
直线、射线、线段
知识要点1
已知A,B,C,D四个点。
(1)画直线AB,AD;
(2)画射线AC,BC;
(3)画线段DC,BD。
.A
.B
.C
.D
直线、射线、线段各有什么特点?
线段:有两个端点,不可以延长,可以度量。
射线:有一个端点,另一端可以无限延长,不可以度量。
直线:没有端点,可以无限延长,不可以度量。
2.写出钟面上分针和时针所组成的角是什么角
角的分类
知识要点2
( )
( )
( )
该怎样判别它们分别是什么角呢?
名称 度数 与直角的关系
锐角
直角
钝角
平角
周角
锐角<90°
1直角 = 90°
90°<钝角<180°
平角 = 180°
周角 = 360°
比直角小
比直角大
平角 = 2直角
周角 = 4直角
钝角
直角
锐角
2.写出钟面上分针和时针所组成的角是什么角
( )
( )
( )
画角
知识要点3
以点A为顶点画一个80°的角,再以点B为顶点画一个30°的角,组成一个三角形。请你量出三角形中第三个角的度数,并标出来。
你知道画角的方法吗?
A B
用量角器画60°角的方法
(1)先画一条射线,使量角器的中心和射线的端点
重合,0°刻度线和射线重合。
(2)在量角器60°刻度线的地方点一个点。
(3)以画出的射线的端点为端点,通过刚画的点,
再画一条射线。
A B
80°
30°
70°
以点A为顶点画一个80°的角,再以点B为顶点画一个30°的角,组成一个三角形。请你量出三角形中第三个角的度数,并标出来。
画垂线的实际应用
知识要点4
4.在下面平行线间画一个最大的正方形。
正方形的四个角都是直角,所以需要在两条平行线之间画垂线,你会画垂线吗?
过直线上一点(直线外一点)画垂线的方法
1.边线重合。
3.画线标号。
2.平移到点。
A
B
C
D
ACDB 即为最大的正方形。
4.在下面平行线间画一个最大的正方形。
图形的分类
知识要点5
5.把下面图形分一分。
三角形
四边形
圆
名称 图例 特点
长方形
正方形
平 行 四边形
三角形
梯 形
圆 形
对边相等,四个角都是直角。
四条边都相等,四个角都是直角。
对边平行且相等,相对的角相等。
由三条线段围成,内角和是180°。
只有一组对边平行的四边形。
在同圆(等圆)中,所有的半径都相等,所有的直径都相等。
三角形的内角和
知识要点6
6.已知等腰三角形的风筝,一个底角70°,顶
角多少度?
三角形的内角和是180°。
方法一: 180°-70°-70°=40°
70°
70°
?
方法二: 180°-70°×2=40°
答:顶角是40°。
课堂练习
1.填表。
(教材第95页练习二十二第2题)
名称 锐角 钝角 直角 平角 周角
图形
特征 小于90°
大于90°
等于90°
等于180°
等于360°
2.先估计下面角的度数,再用量角器量一量。
估计( )
测量( )
估计( )
测量( )
估计( )
测量( )
60°
58°
120°
128°
80°
85°
(教材第95页练习二十二第3题)
(1)从下面 4 条线段中选 3 条围成一个三角形,只
能选( )。
3.填一填。
①
③
④
②
(2)一个等腰三角形的顶角是 60°,它的一个底角
是( )。
(教材第95页练习二十二第4题)
②
③
④
60°
(1)将一张圆形纸片至少对折( )次可以得 到这个圆的圆心。
(2)圆的位置是由( )决定的,圆的大小是由( )或( )决定的。
A
A. 2 B. 3 C.1
A. 圆心 B. 半径 C.直径 D.高
A
B
C
4.填空。
(3)把一个等边三角形沿一条高分开,分成的直角三角形的两个锐角的度数分别是( ) °和( ) °。
4.填空。
A. 90 B. 60 C.30
等边三角形的三个角都是60°。
B
C
5.判断。
(1)一个三角形里如果有一个直角,必定是一个直角三角形。( )
(2)一个直角三角形两个锐角相差14度,两个锐角分别是38°和53°。( )
(3)一个等边三角形,从一个顶点起,用一条线段把它分成大小相等的两个三角形,其中一个三角形的内角和是180°。( )
√
×
√
(4)不相交的两条线叫平行线。( )
(5)等边三角形一定是等腰三角形。( ) (6)直角的两条边是直线。( ) (7)平角是一条直线。( )
×
√
×
×
作业课件中的相关练习。
02
01
练习二十二。
课后作业
第8课时 平面图形的认识
总复习
五
西师版数学六年级(下)
1.回顾并牢固掌握平面图形的基本特征,明确概念间的区别和联系。
2.把握平面图形间的相互联系,进行完整的知识建构,培养空间观念。
3.在整理复习中运用分类整理的方法,培养对比分析、归纳整理的能力,在小组活动中培养学生合作学习的能力。
学习目标
【重点】
能对平面图形进行分类,掌握直线、射线和线段的
联系和区别。
【难点】
角的度量和平行线的画法。
知识梳理
想一想,我们都学过哪些平面图形?
平面图形
不封闭图形
封闭图形
不封闭图形
直线、 射线 、线段
角
平行线 相交线
封闭图形
长方形
正方形
平行四边形
三角形
梯形
圆
四边形
直线、射线、线段
●
●
●
线段:
射线:
直线:
有两个端点,不可以延长,可以度量。
有一个端点,另一端可以无限延长,不可以度量。
没有端点,可以无限延长,不可以度量。
直线、射线和线段有什么区别?
●
●
●
线段:
射线:
有两个端点,不可以延长,可以度量。
有一个端点,另一端可以无限延长,不可以度量。
线段向两方延长,射线向反向延长,
都可以得到直线。若线段向一方延
长可得射线。
没有端点,可以无限延长,不可以度量。
●
●
●
在直线上取两点可以得到一条线段,取一点可以得到两条射线。所以它们都是直线的一部分。
直线的基本性质:两点确定一条直线。
线段的基本性质:两点之间,线段最短。
直线:
同一平面内的两条直线有几种位置关系?
互相平行
同一平面内两条直线的位置关系:
相交
相交或平行。
角
我们学过的角有哪几种?角的大小和什么有关?
两条直线
平行
相交
平行线
角
角
我们学过的角有哪几种?角的大小和什么有关?
角
锐角
直角
钝角
平角
周角
相互垂直成90°的角
小于90°的角
大于90°而小于180°的角
等于180°的角
等于360°的角
角的大小要看两边叉开的大小,叉开得越大,角越大。角的大小与角的两边所画出的长短没有联系。
封闭图形
三角形
多边形
圆
四边形
由曲线围成的封闭图形
三角形、四边形、圆
三角形
锐角三角形
直角三角形
钝角三角形
按角分
不等边三角形
等腰三角形
按边分
等边三角形
等腰三角形
三角形
等边三角形
三角形、四边形、圆
四边形
不规则四边形
平行四边形
三角形、四边形、圆
梯形
等腰梯形
一般梯形
四个角都
是直角
长方形
四个边
都相等
正方形
直角梯形
三角形
高
底
高
下底
上底
底
高
平行四边形
梯形
三角形有三条高。
平行四边形有两组对边平行且相等 平行线间的距离处处相等,即平行线间任何一条距离都是高。它有无数高。
梯形有一组对
边平行,有无
数高。
三角形内角和是180°。
O
r
d
圆内有无数条半径和直径,同一圆内直径等于半径的2倍。
连接圆心和圆上任意一点的线段叫做圆的半径, 通过圆心且两个端点都在圆周上的线段叫做圆的直径。 所有直径和半径都相等。
圆心决定圆的位置,半径决定圆的大小。圆是轴对称图形,有无数条对称轴。
要点回顾
1.按要求画图。
直线、射线、线段
知识要点1
已知A,B,C,D四个点。
(1)画直线AB,AD;
(2)画射线AC,BC;
(3)画线段DC,BD。
.A
.B
.C
.D
直线、射线、线段各有什么特点?
线段:有两个端点,不可以延长,可以度量。
射线:有一个端点,另一端可以无限延长,不可以度量。
直线:没有端点,可以无限延长,不可以度量。
2.写出钟面上分针和时针所组成的角是什么角
角的分类
知识要点2
( )
( )
( )
该怎样判别它们分别是什么角呢?
名称 度数 与直角的关系
锐角
直角
钝角
平角
周角
锐角<90°
1直角 = 90°
90°<钝角<180°
平角 = 180°
周角 = 360°
比直角小
比直角大
平角 = 2直角
周角 = 4直角
钝角
直角
锐角
2.写出钟面上分针和时针所组成的角是什么角
( )
( )
( )
画角
知识要点3
以点A为顶点画一个80°的角,再以点B为顶点画一个30°的角,组成一个三角形。请你量出三角形中第三个角的度数,并标出来。
你知道画角的方法吗?
A B
用量角器画60°角的方法
(1)先画一条射线,使量角器的中心和射线的端点
重合,0°刻度线和射线重合。
(2)在量角器60°刻度线的地方点一个点。
(3)以画出的射线的端点为端点,通过刚画的点,
再画一条射线。
A B
80°
30°
70°
以点A为顶点画一个80°的角,再以点B为顶点画一个30°的角,组成一个三角形。请你量出三角形中第三个角的度数,并标出来。
画垂线的实际应用
知识要点4
4.在下面平行线间画一个最大的正方形。
正方形的四个角都是直角,所以需要在两条平行线之间画垂线,你会画垂线吗?
过直线上一点(直线外一点)画垂线的方法
1.边线重合。
3.画线标号。
2.平移到点。
A
B
C
D
ACDB 即为最大的正方形。
4.在下面平行线间画一个最大的正方形。
图形的分类
知识要点5
5.把下面图形分一分。
三角形
四边形
圆
名称 图例 特点
长方形
正方形
平 行 四边形
三角形
梯 形
圆 形
对边相等,四个角都是直角。
四条边都相等,四个角都是直角。
对边平行且相等,相对的角相等。
由三条线段围成,内角和是180°。
只有一组对边平行的四边形。
在同圆(等圆)中,所有的半径都相等,所有的直径都相等。
三角形的内角和
知识要点6
6.已知等腰三角形的风筝,一个底角70°,顶
角多少度?
三角形的内角和是180°。
方法一: 180°-70°-70°=40°
70°
70°
?
方法二: 180°-70°×2=40°
答:顶角是40°。
课堂练习
1.填表。
(教材第95页练习二十二第2题)
名称 锐角 钝角 直角 平角 周角
图形
特征 小于90°
大于90°
等于90°
等于180°
等于360°
2.先估计下面角的度数,再用量角器量一量。
估计( )
测量( )
估计( )
测量( )
估计( )
测量( )
60°
58°
120°
128°
80°
85°
(教材第95页练习二十二第3题)
(1)从下面 4 条线段中选 3 条围成一个三角形,只
能选( )。
3.填一填。
①
③
④
②
(2)一个等腰三角形的顶角是 60°,它的一个底角
是( )。
(教材第95页练习二十二第4题)
②
③
④
60°
(1)将一张圆形纸片至少对折( )次可以得 到这个圆的圆心。
(2)圆的位置是由( )决定的,圆的大小是由( )或( )决定的。
A
A. 2 B. 3 C.1
A. 圆心 B. 半径 C.直径 D.高
A
B
C
4.填空。
(3)把一个等边三角形沿一条高分开,分成的直角三角形的两个锐角的度数分别是( ) °和( ) °。
4.填空。
A. 90 B. 60 C.30
等边三角形的三个角都是60°。
B
C
5.判断。
(1)一个三角形里如果有一个直角,必定是一个直角三角形。( )
(2)一个直角三角形两个锐角相差14度,两个锐角分别是38°和53°。( )
(3)一个等边三角形,从一个顶点起,用一条线段把它分成大小相等的两个三角形,其中一个三角形的内角和是180°。( )
√
×
√
(4)不相交的两条线叫平行线。( )
(5)等边三角形一定是等腰三角形。( ) (6)直角的两条边是直线。( ) (7)平角是一条直线。( )
×
√
×
×
作业课件中的相关练习。
02
01
练习二十二。
课后作业
