数学六年级下册西师大版 五总复习—第11课时 立体图形 课件(共48张PPT)
文档属性
| 名称 | 数学六年级下册西师大版 五总复习—第11课时 立体图形 课件(共48张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-01 00:00:00 | ||
图片预览







文档简介
(共48张PPT)
第11课时 立体图形
总复习
五
西师版数学六年级(下)
1.通过复习,进一步认识长方体、正方体、圆柱、圆锥等图形,掌握它们的特征,把握有关图形之间的相互联系。
2.掌握所学的立体图形的表面积和体积的含义,会计算它们的表面积和体积,并解决简单的实际问题。
3.在解决问题的过程中,体会知识与生活之间的联系,增强应用数学的意识,体会数学的魅力。
学习目标
【重点】
能正确计算常见立体图形的表面积和体积,并解决一些
简单的实际问题。
【难点】
感受数学知识和方法的内在联系,体会转化、
类比等数学思想方法,发展初步推理能力。
知识梳理
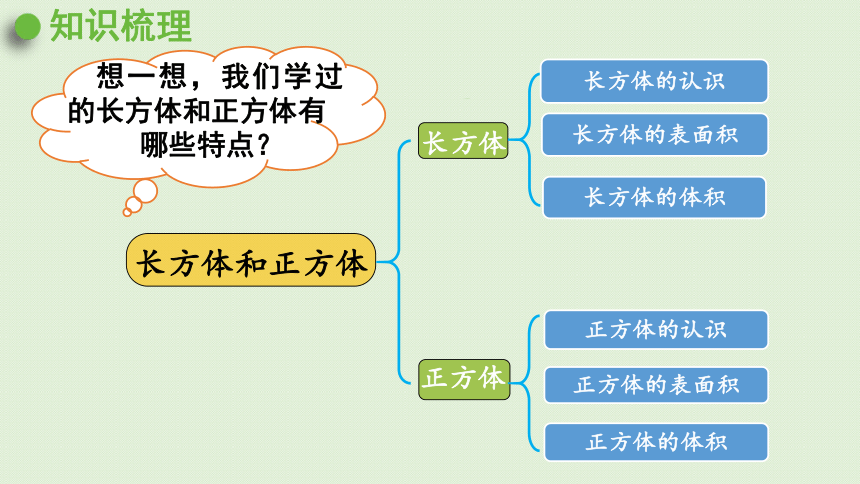
想一想,我们学过的长方体和正方体有
哪些特点?
长方体和正方体
长方体
长方体的认识
长方体的表面积
长方体的体积
正方体
正方体的认识
正方体的体积
正方体的表面积
长方体和正方体的认识
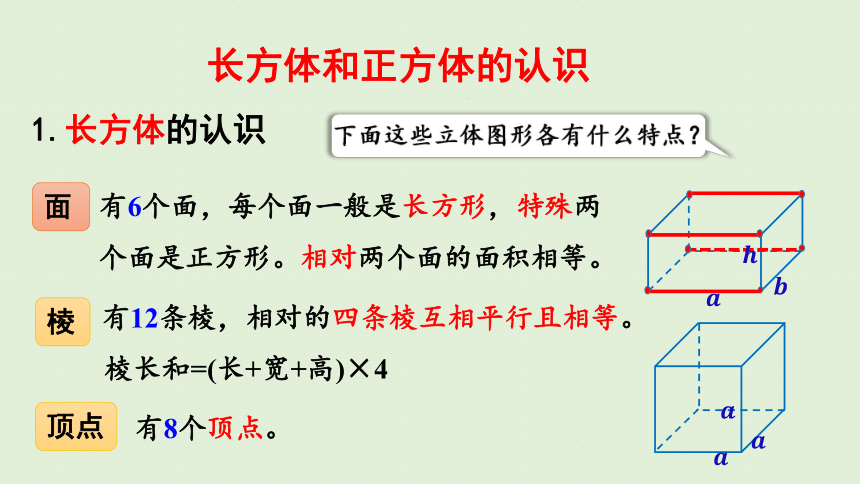
1.长方体的认识
下面这些立体图形各有什么特点?
面
有6个面,每个面一般是长方形,特殊两个面是正方形。相对两个面的面积相等。
有12条棱,相对的四条棱互相平行且相等。
棱
棱长和=(长+宽+高)×4
有8个顶点。
顶点
有6个面,每个面都是正方形,每个面面积都相等。
有12条棱,每条棱长度都相等。
棱长和=棱长×12
有8个顶点。
长方体和正方体的认识
2.正方体的认识
面
棱
顶点
立体图形 相同点 不同点 关系
面 棱 点 面的形状 面积 棱长
长方体
正方体
长方体与正方体的相同点与不同点
6个
12条
8个
6个面一般是长方形,也有可能有两个相对的面是正方形。
6个面都是相等的正方形。
相对的面的面积相等。
6个面的面积都相等。
每一组互相平行的四条棱长相等。
12条棱长度相等。
正方体是特殊的长方体。
长方体
正方体
想一想,我们学过的圆柱和圆锥有哪些
特点?
圆柱和圆锥
圆柱
圆柱的认识
圆柱的表面积
圆柱的体积
圆锥
圆锥的认识
圆锥的体积
圆柱和圆锥的认识
圆心O
.
半径r
高 h
直径 d
侧面
.
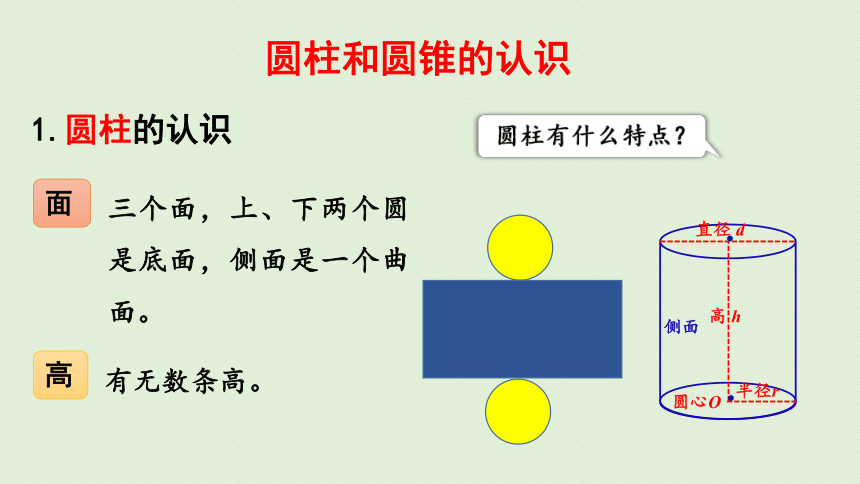
1.圆柱的认识
圆柱有什么特点?
三个面,上、下两个圆是底面,侧面是一个曲面。
有无数条高。
面
高
圆柱和圆锥的认识
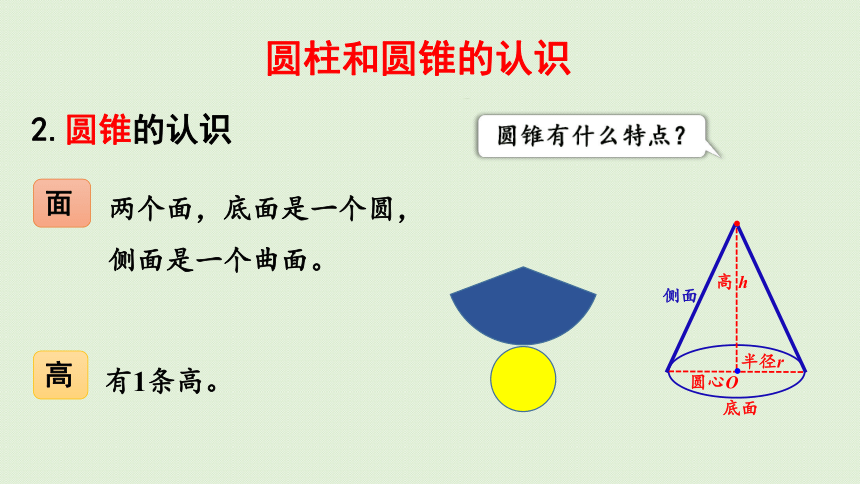
2.圆锥的认识
圆锥有什么特点?
两个面,底面是一个圆,侧面是一个曲面。
有1条高。
面
高
.
半径r
高 h
侧面
底面
圆心O
.
立体图形 底面 侧面 高
圆柱 两个完全相同的面 展开是一个长方形或正方形 两底面之间的距离(无数条)
圆锥 一个圆 展开是个扇形 顶点到底面的距离(一条)
圆柱和圆锥的认识
3.圆柱和圆锥之间的关系
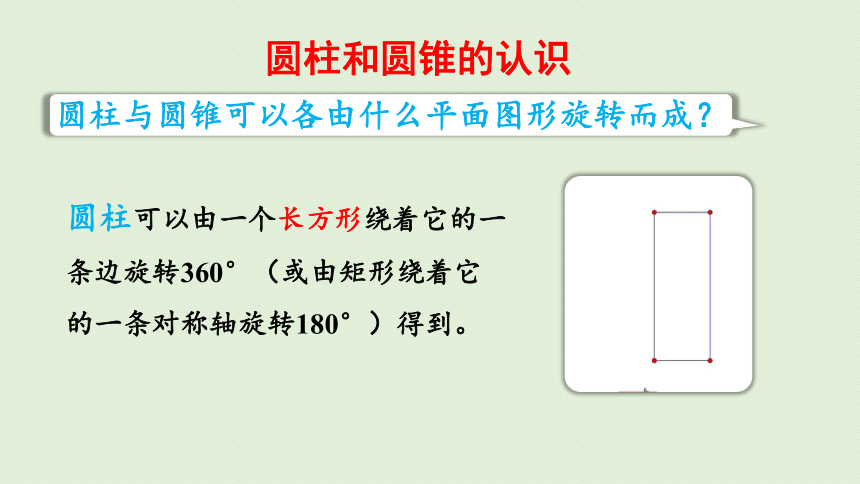
圆柱与圆锥可以各由什么平面图形旋转而成?
圆柱可以由一个长方形绕着它的一
条边旋转360°(或由矩形绕着它
的一条对称轴旋转180°)得到。
圆柱和圆锥的认识
圆柱与圆锥可以各由什么平面图形旋转而成?
圆锥可以由一个直角三角形绕着它的一条直角边旋转360°得到。
圆柱和圆锥的认识
长方体的表面积是6个面的面积和。
长方体和正方体的表面积
1.长方体的表面积
上
下
后
前
左
右
长方体和正方体的表面积
1.长方体的表面积
上
下
后
前
左
右
长方体相对面的面积相等。
长×高
长×宽
宽×高
表面积=(长×宽+长×高+宽×高)×2
S=2(b+h+bh)
正方体的表面积是6个面的面积和。
长方体和正方体的表面积
2.正方体的表面积
上
下
后
前
左
右
长方体和正方体的表面积
2.正方体的表面积
上
下
后
前
左
右
正方体6个面都是相等的正方形。
表面积=棱长×棱长×6
S=6
长()
宽()
高()
长方体的体积=长×宽×高
V =bh
棱长()
棱长()
棱长()
正方体的体积=棱长×棱长×棱长
V =
长方体和正方体体积的统一公式=底面积×高
V = Sh
常用的体积单位有cm 、dm 、m 。
长方体和正方体的体积
圆柱的侧面沿高展开是长方形,展开的长方形的长相当于圆柱的底面周长,宽相当于圆柱的高。
侧面积=底面周长×高
S侧=Ch
底面积=底面半径 ×圆周率×2
S底=2πr
表面积=底面积+侧面积
S表=2πr(r+h)
圆心O
.
半径r
高 h
直径 d
侧面
.
圆柱的表面积
圆柱和圆锥的体积
圆柱的体积
体积=底面积×高
V=
圆心O
.
半径r
高 h
直径 d
侧面
.
体积=底面积×高÷3
V =
.
半径r
高 h
侧面
底面
圆心O
.
圆锥的体积
圆锥的体积等于与它等底等高的圆柱体积的三分之一。
要点回顾
求立体图形的表面积
知识要点1
求需要多少硬纸片,就是求长方体的表面积。
1.要在下图的六个面上贴上硬纸片,至少需要多少平方
厘米硬纸片?
6 cm
3 cm
3 cm
S=2(b+h+bh)
(6×3+3×3+6×3)×2
= 45×2
= 90(cm )
答:至少需要90 cm 硬纸片。
2.一个无盖玻璃鱼缸的形状是正方体,棱长3 dm。制作
这个 鱼缸时至少需要多少平方分米玻璃?
这个正方体5个面的面积之和是棱长×棱长×5。
3×3×5=45(平方分米)
答:制作这个鱼缸时至少需要45平方分米玻璃。
3. 一顶圆柱形厨师帽,高30 cm,帽顶直径20 cm,做这
样一顶帽子至少需要用多少平方厘米的面料?(得数
保留整十数)
这个帽子是什么样的,它由哪几面组成?
“没有底”的帽子的展开图,它是由一个底面和一个侧面组成。
帽子面积=2r×高+r2
帽子的侧面积:3.14×20×30=1884(平方厘米)
帽顶的面积:3.14×(20÷2)2 =314(平方厘米)
需要面料面积:1884+314=2198 ≈ 2200(平方厘米)
答:做这样一顶帽子至少需要用2200平方厘米的面料。
3. 一顶圆柱形厨师帽,高30 cm,帽顶直径20 cm,做这
样一顶帽子至少需要用多少平方厘米的面料?(得数
保留整十数)
4.一个正方体的棱长总和是108厘米,它的体积是多少?
求立体图形的体积
知识要点2
正方体棱长总和=棱长×12
108÷12=9(厘米)
9×9×9=729(立方厘米)
V=a
答:它的体积是729立方厘米。
5.一根长方体木料,长5 m,横截面的面积是0.06 m2。
这根木料的体积是多少?
0.06 m2
长方体体积=底面积×高
0.06×5=0.3(m3)
答:这根木料的体积是0.3m3。
6.工地上有一堆沙子,近似于一个圆锥(如下图)。这
堆沙子的体积大约是多少?如果每立方米沙子重1.5 t,
那么这堆沙子大约重多少吨?
4 m
1.5 m
V=
沙堆的底面积:
3.14 ×(4÷2)2 =12.56(m2)
沙堆的重量:6.28×1.5=9.42(t)
沙堆的体积:
12.56 ×1.5 ×=6.28(m3)
答:这堆沙子大约6.28 m3。
答:这堆沙子大约重9.42 t。
7.填一填。
从不同位置位置观察同一物体
知识要点3
不同位置观察一个立体图形,所看到的形状一般不同。
从( )看
从( )看
从( )看
左面
前面
上面
8.这3个图形,从哪面看到的图形相同?从哪面看到的图形不同?
从同一位置位置观察不同物体
知识要点4
不同形状的立体图形从同一方向进行观察,所看到的形状可能不同,也可能相同。
形状相同的
从上面看
从左面看
→
→
形状不相同的
从前面看
→
8.按从不同方向看到的图形摆出几何体。
根据平面图形摆几何体
知识要点5
搭几何体时,先从一个方向确定基本形状,然后从另外两面确定层数和每层的个数。
(1)
左面
上面
正面
(2)
左面
上面
正面
8.按从不同方向看到的图形摆出几何体。
课堂练习
1. 判断下列说法是否正确。
(教材第100页练习二十三第1题)
(1)用3个同样大小的正方体拼成一个长方体,长方
体的表面积是正方体的3倍。
(2)圆柱底面的直径是5 cm,高也是5 cm,它的侧面
展开图是一个正方形。
(3)把一个体积是15 cm3的圆柱削成一个体积最大的
圆锥,圆锥的体积是5 cm3。
×
×
√
2.下面第1排中的平面图形绕红线旋转1周能形成第2排的
哪个立体图形?(连线)
(教材第100页练习二十三第3题)
3.计算下面各图的表面积和体积。(图中单位:cm)
(教材第100页练习二十三第4题)
表面积:
(15×10+8×10+15×8)×2
=700(cm2)
体积:
15×10×8=1200(cm3)
3.计算下面各图的表面积和体积。(图中单位:cm)
(教材第100页练习二十三第4题)
表面积:
6×10×10=600(cm2)
体积:
10×10×10=1000(cm3)
3.计算下面各图的表面积和体积。(图中单位:cm)
(教材第100页练习二十三第4题)
表面积:
2×3.14×42+3.14×8×12
=401.92(cm2)
体积:
3.14×42×12=602.88(cm3)
4.下面这个容器一共能装多少毫升水?(容器壁的厚度
忽略不计。)
(教材第101页练习二十三第5题)
8×5×2+3.14×(4÷2)2×3
=117.68(dm3)
=117680(mL)
答:这个容器能装117680毫升水。
5. 一台长方体形冰箱长0.6 m,宽0.5 m,高1.8 m。
(1)做这台冰箱的包装盒至少需要纸板多少平方米?
(2)这台冰箱占地面积是多少平方米?
(教材第101页练习二十三第6题)
(1)(0.6×0.5+0.6×1.8+0.5×1.8)×2=4.56(m2)
答:做这台冰箱的包装盒至少需要纸板4.56平方米。
(2)0.6×0.5=0.3(m2)
答:这台冰箱占地面积是0.3平方米。
6.一条水渠长800 m,横截面如下图。
(教材第101页练习二十三第7题)
(1)水渠的横截面积是多少平方米?
4×2.5=10(平方米)
答:水渠的横截面积是10平方米。
(2)水渠水深2 m,水在水渠中每分流动20 m,该水渠
每时的水流量是多少立方米?
2×4×20×60=9600(立方米)
答:该水渠每时的水流量是9600立方米。
(教材第101页练习二十三第7题)
7.学校修建花园需要40吨沙,这堆沙够用吗?(每立方
米沙重1.8 吨。)
(教材第101页练习二十三第8题)
沙堆半径:
12.56÷3.14÷2=2(米)
沙堆体积:
×3.14×22×1.2=5.024(立方米)
沙堆重:
5.024×1.8=9.0432(吨)
9.0432<40
答:这堆沙不够用。
7.学校修建花园需要40吨沙,这堆沙够用吗?(每立方
米沙重1.8 吨。)
(教材第101页练习二十三第8题)
8.把两个完全一样的小长方体木块粘成一个大长方体,
这个大长方体的表面积比原来两个小长方体的表面
积的和减少50 cm 。如果拼成的大长方体长20 cm,
那么一个小长方体的体积是多少立方厘米?
V=Sh
减少了两个侧面的面积。
一个侧面的面积:50÷2=25(cm )
小长方体的高:20÷2=10(cm)
(50÷2)×(20÷2)=250(cm )
答:一个小长方体的体积是250 cm 。
8.把两个完全一样的小长方体木块粘成一个大长方体,
这个大长方体的表面积比原来两个小长方体的表面
积的和减少50 cm 。如果拼成的大长方体长20 cm,
那么一个小长方体的体积是多少立方厘米?
9.一个圆锥形沙堆,底面积是28.26 m2,高是2.5 m。用
这堆沙在10 m宽的公路上铺2 cm厚的路面,能铺多少
米?
=23.55(m )
×28.26×2.5
(1)沙堆的体积:
(2)所铺公路的长度:
23.55÷10÷0.02
=2.355÷0.02
=117.75(m)
=9.42×2.5
答:能铺117.75 m。
2 cm=0.02 m
注意单位转换哦!
作业课件中的相关练习。
02
01
练习二十三。
课后作业
第11课时 立体图形
总复习
五
西师版数学六年级(下)
1.通过复习,进一步认识长方体、正方体、圆柱、圆锥等图形,掌握它们的特征,把握有关图形之间的相互联系。
2.掌握所学的立体图形的表面积和体积的含义,会计算它们的表面积和体积,并解决简单的实际问题。
3.在解决问题的过程中,体会知识与生活之间的联系,增强应用数学的意识,体会数学的魅力。
学习目标
【重点】
能正确计算常见立体图形的表面积和体积,并解决一些
简单的实际问题。
【难点】
感受数学知识和方法的内在联系,体会转化、
类比等数学思想方法,发展初步推理能力。
知识梳理
想一想,我们学过的长方体和正方体有
哪些特点?
长方体和正方体
长方体
长方体的认识
长方体的表面积
长方体的体积
正方体
正方体的认识
正方体的体积
正方体的表面积
长方体和正方体的认识
1.长方体的认识
下面这些立体图形各有什么特点?
面
有6个面,每个面一般是长方形,特殊两个面是正方形。相对两个面的面积相等。
有12条棱,相对的四条棱互相平行且相等。
棱
棱长和=(长+宽+高)×4
有8个顶点。
顶点
有6个面,每个面都是正方形,每个面面积都相等。
有12条棱,每条棱长度都相等。
棱长和=棱长×12
有8个顶点。
长方体和正方体的认识
2.正方体的认识
面
棱
顶点
立体图形 相同点 不同点 关系
面 棱 点 面的形状 面积 棱长
长方体
正方体
长方体与正方体的相同点与不同点
6个
12条
8个
6个面一般是长方形,也有可能有两个相对的面是正方形。
6个面都是相等的正方形。
相对的面的面积相等。
6个面的面积都相等。
每一组互相平行的四条棱长相等。
12条棱长度相等。
正方体是特殊的长方体。
长方体
正方体
想一想,我们学过的圆柱和圆锥有哪些
特点?
圆柱和圆锥
圆柱
圆柱的认识
圆柱的表面积
圆柱的体积
圆锥
圆锥的认识
圆锥的体积
圆柱和圆锥的认识
圆心O
.
半径r
高 h
直径 d
侧面
.
1.圆柱的认识
圆柱有什么特点?
三个面,上、下两个圆是底面,侧面是一个曲面。
有无数条高。
面
高
圆柱和圆锥的认识
2.圆锥的认识
圆锥有什么特点?
两个面,底面是一个圆,侧面是一个曲面。
有1条高。
面
高
.
半径r
高 h
侧面
底面
圆心O
.
立体图形 底面 侧面 高
圆柱 两个完全相同的面 展开是一个长方形或正方形 两底面之间的距离(无数条)
圆锥 一个圆 展开是个扇形 顶点到底面的距离(一条)
圆柱和圆锥的认识
3.圆柱和圆锥之间的关系
圆柱与圆锥可以各由什么平面图形旋转而成?
圆柱可以由一个长方形绕着它的一
条边旋转360°(或由矩形绕着它
的一条对称轴旋转180°)得到。
圆柱和圆锥的认识
圆柱与圆锥可以各由什么平面图形旋转而成?
圆锥可以由一个直角三角形绕着它的一条直角边旋转360°得到。
圆柱和圆锥的认识
长方体的表面积是6个面的面积和。
长方体和正方体的表面积
1.长方体的表面积
上
下
后
前
左
右
长方体和正方体的表面积
1.长方体的表面积
上
下
后
前
左
右
长方体相对面的面积相等。
长×高
长×宽
宽×高
表面积=(长×宽+长×高+宽×高)×2
S=2(b+h+bh)
正方体的表面积是6个面的面积和。
长方体和正方体的表面积
2.正方体的表面积
上
下
后
前
左
右
长方体和正方体的表面积
2.正方体的表面积
上
下
后
前
左
右
正方体6个面都是相等的正方形。
表面积=棱长×棱长×6
S=6
长()
宽()
高()
长方体的体积=长×宽×高
V =bh
棱长()
棱长()
棱长()
正方体的体积=棱长×棱长×棱长
V =
长方体和正方体体积的统一公式=底面积×高
V = Sh
常用的体积单位有cm 、dm 、m 。
长方体和正方体的体积
圆柱的侧面沿高展开是长方形,展开的长方形的长相当于圆柱的底面周长,宽相当于圆柱的高。
侧面积=底面周长×高
S侧=Ch
底面积=底面半径 ×圆周率×2
S底=2πr
表面积=底面积+侧面积
S表=2πr(r+h)
圆心O
.
半径r
高 h
直径 d
侧面
.
圆柱的表面积
圆柱和圆锥的体积
圆柱的体积
体积=底面积×高
V=
圆心O
.
半径r
高 h
直径 d
侧面
.
体积=底面积×高÷3
V =
.
半径r
高 h
侧面
底面
圆心O
.
圆锥的体积
圆锥的体积等于与它等底等高的圆柱体积的三分之一。
要点回顾
求立体图形的表面积
知识要点1
求需要多少硬纸片,就是求长方体的表面积。
1.要在下图的六个面上贴上硬纸片,至少需要多少平方
厘米硬纸片?
6 cm
3 cm
3 cm
S=2(b+h+bh)
(6×3+3×3+6×3)×2
= 45×2
= 90(cm )
答:至少需要90 cm 硬纸片。
2.一个无盖玻璃鱼缸的形状是正方体,棱长3 dm。制作
这个 鱼缸时至少需要多少平方分米玻璃?
这个正方体5个面的面积之和是棱长×棱长×5。
3×3×5=45(平方分米)
答:制作这个鱼缸时至少需要45平方分米玻璃。
3. 一顶圆柱形厨师帽,高30 cm,帽顶直径20 cm,做这
样一顶帽子至少需要用多少平方厘米的面料?(得数
保留整十数)
这个帽子是什么样的,它由哪几面组成?
“没有底”的帽子的展开图,它是由一个底面和一个侧面组成。
帽子面积=2r×高+r2
帽子的侧面积:3.14×20×30=1884(平方厘米)
帽顶的面积:3.14×(20÷2)2 =314(平方厘米)
需要面料面积:1884+314=2198 ≈ 2200(平方厘米)
答:做这样一顶帽子至少需要用2200平方厘米的面料。
3. 一顶圆柱形厨师帽,高30 cm,帽顶直径20 cm,做这
样一顶帽子至少需要用多少平方厘米的面料?(得数
保留整十数)
4.一个正方体的棱长总和是108厘米,它的体积是多少?
求立体图形的体积
知识要点2
正方体棱长总和=棱长×12
108÷12=9(厘米)
9×9×9=729(立方厘米)
V=a
答:它的体积是729立方厘米。
5.一根长方体木料,长5 m,横截面的面积是0.06 m2。
这根木料的体积是多少?
0.06 m2
长方体体积=底面积×高
0.06×5=0.3(m3)
答:这根木料的体积是0.3m3。
6.工地上有一堆沙子,近似于一个圆锥(如下图)。这
堆沙子的体积大约是多少?如果每立方米沙子重1.5 t,
那么这堆沙子大约重多少吨?
4 m
1.5 m
V=
沙堆的底面积:
3.14 ×(4÷2)2 =12.56(m2)
沙堆的重量:6.28×1.5=9.42(t)
沙堆的体积:
12.56 ×1.5 ×=6.28(m3)
答:这堆沙子大约6.28 m3。
答:这堆沙子大约重9.42 t。
7.填一填。
从不同位置位置观察同一物体
知识要点3
不同位置观察一个立体图形,所看到的形状一般不同。
从( )看
从( )看
从( )看
左面
前面
上面
8.这3个图形,从哪面看到的图形相同?从哪面看到的图形不同?
从同一位置位置观察不同物体
知识要点4
不同形状的立体图形从同一方向进行观察,所看到的形状可能不同,也可能相同。
形状相同的
从上面看
从左面看
→
→
形状不相同的
从前面看
→
8.按从不同方向看到的图形摆出几何体。
根据平面图形摆几何体
知识要点5
搭几何体时,先从一个方向确定基本形状,然后从另外两面确定层数和每层的个数。
(1)
左面
上面
正面
(2)
左面
上面
正面
8.按从不同方向看到的图形摆出几何体。
课堂练习
1. 判断下列说法是否正确。
(教材第100页练习二十三第1题)
(1)用3个同样大小的正方体拼成一个长方体,长方
体的表面积是正方体的3倍。
(2)圆柱底面的直径是5 cm,高也是5 cm,它的侧面
展开图是一个正方形。
(3)把一个体积是15 cm3的圆柱削成一个体积最大的
圆锥,圆锥的体积是5 cm3。
×
×
√
2.下面第1排中的平面图形绕红线旋转1周能形成第2排的
哪个立体图形?(连线)
(教材第100页练习二十三第3题)
3.计算下面各图的表面积和体积。(图中单位:cm)
(教材第100页练习二十三第4题)
表面积:
(15×10+8×10+15×8)×2
=700(cm2)
体积:
15×10×8=1200(cm3)
3.计算下面各图的表面积和体积。(图中单位:cm)
(教材第100页练习二十三第4题)
表面积:
6×10×10=600(cm2)
体积:
10×10×10=1000(cm3)
3.计算下面各图的表面积和体积。(图中单位:cm)
(教材第100页练习二十三第4题)
表面积:
2×3.14×42+3.14×8×12
=401.92(cm2)
体积:
3.14×42×12=602.88(cm3)
4.下面这个容器一共能装多少毫升水?(容器壁的厚度
忽略不计。)
(教材第101页练习二十三第5题)
8×5×2+3.14×(4÷2)2×3
=117.68(dm3)
=117680(mL)
答:这个容器能装117680毫升水。
5. 一台长方体形冰箱长0.6 m,宽0.5 m,高1.8 m。
(1)做这台冰箱的包装盒至少需要纸板多少平方米?
(2)这台冰箱占地面积是多少平方米?
(教材第101页练习二十三第6题)
(1)(0.6×0.5+0.6×1.8+0.5×1.8)×2=4.56(m2)
答:做这台冰箱的包装盒至少需要纸板4.56平方米。
(2)0.6×0.5=0.3(m2)
答:这台冰箱占地面积是0.3平方米。
6.一条水渠长800 m,横截面如下图。
(教材第101页练习二十三第7题)
(1)水渠的横截面积是多少平方米?
4×2.5=10(平方米)
答:水渠的横截面积是10平方米。
(2)水渠水深2 m,水在水渠中每分流动20 m,该水渠
每时的水流量是多少立方米?
2×4×20×60=9600(立方米)
答:该水渠每时的水流量是9600立方米。
(教材第101页练习二十三第7题)
7.学校修建花园需要40吨沙,这堆沙够用吗?(每立方
米沙重1.8 吨。)
(教材第101页练习二十三第8题)
沙堆半径:
12.56÷3.14÷2=2(米)
沙堆体积:
×3.14×22×1.2=5.024(立方米)
沙堆重:
5.024×1.8=9.0432(吨)
9.0432<40
答:这堆沙不够用。
7.学校修建花园需要40吨沙,这堆沙够用吗?(每立方
米沙重1.8 吨。)
(教材第101页练习二十三第8题)
8.把两个完全一样的小长方体木块粘成一个大长方体,
这个大长方体的表面积比原来两个小长方体的表面
积的和减少50 cm 。如果拼成的大长方体长20 cm,
那么一个小长方体的体积是多少立方厘米?
V=Sh
减少了两个侧面的面积。
一个侧面的面积:50÷2=25(cm )
小长方体的高:20÷2=10(cm)
(50÷2)×(20÷2)=250(cm )
答:一个小长方体的体积是250 cm 。
8.把两个完全一样的小长方体木块粘成一个大长方体,
这个大长方体的表面积比原来两个小长方体的表面
积的和减少50 cm 。如果拼成的大长方体长20 cm,
那么一个小长方体的体积是多少立方厘米?
9.一个圆锥形沙堆,底面积是28.26 m2,高是2.5 m。用
这堆沙在10 m宽的公路上铺2 cm厚的路面,能铺多少
米?
=23.55(m )
×28.26×2.5
(1)沙堆的体积:
(2)所铺公路的长度:
23.55÷10÷0.02
=2.355÷0.02
=117.75(m)
=9.42×2.5
答:能铺117.75 m。
2 cm=0.02 m
注意单位转换哦!
作业课件中的相关练习。
02
01
练习二十三。
课后作业
