西师大版 数学六年级下册 五、总复习—第5课时 比和比例(课件) (共38张PPT)
文档属性
| 名称 | 西师大版 数学六年级下册 五、总复习—第5课时 比和比例(课件) (共38张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-01 00:00:00 | ||
图片预览







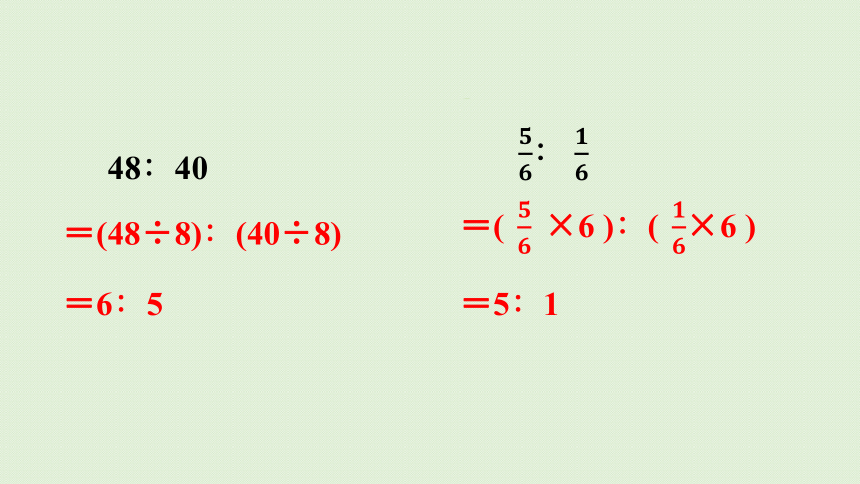


文档简介
(共38张PPT)
第5课时 比和比例
总复习
五
西师版数学六年级(下)
1.进一步掌握比与比例的意义和基本性质,能正确熟练地化简比和求比值。
2.进一步理解正比例和反比例的意义,并能正确判断两种相关联的量成什么比例关系,并能解决简单的实际问题。
3.进一步掌握比例尺的意义,能熟练地应用比例尺的意义解决简单的实际问题。
学习目标
【重点】
掌握比和比例的意义及它们的基本性质,应用
按比例分配和比例尺知识解决问题。
【难点】
正比例和反比例的异同点,优化解决问题
策略。
知识梳理
比和比例
比和比例的 联系与区别
化简比的方法
比值和化简比的区别
化简比 求比值
意义
各部分名称
基本性质
比和比例 的应用
正比例
反比例
比例尺
按比例分配
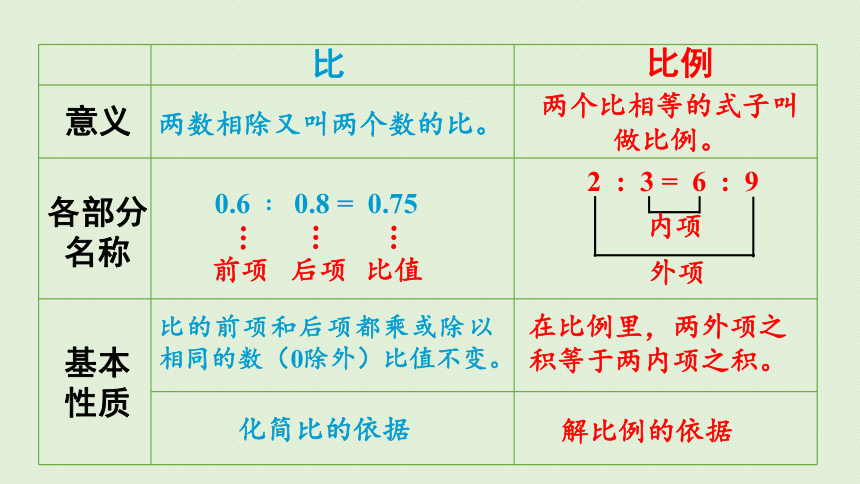
比
比例
意义
各部分名称
基本性质
两数相除又叫两个数的比。
两个比相等的式子叫做比例。
0.6 0.8 = 0.75
前项
后项
比值
…
…
…
2 : 3 = 6 : 9
内项
外项
比的前项和后项都乘或除以相同的数(0除外)比值不变。
在比例里,两外项之积等于两内项之积。
化简比的依据
解比例的依据
要点回顾
1.把下面各比化成最简单的整数比。
化简比
知识要点1
32∶16
48∶40
0.15∶0.3
∶
运用比的基本性质来化简比。
化简比的方法
整数比
小数比
分数比
比的前项和后项同时除以它们的最大公因数。
把比前、后项的小数点向右移动相同的位数,转化成整数比再化简。
把比前、后项同时乘分母的最小公倍数,转化成整数比再化简。
32∶16
0.15∶0.3
=2∶1
=(32÷16) ∶(16÷16)
=(0.15×100)∶(0.3×100)
=(15÷15)∶ (30 ÷15 )
=15∶30
=1∶2
48∶40
=(48÷8)∶(40÷8)
=6∶5
=(×6 )∶(×6 )
=5∶1
∶
2.商店运来一批洗衣机,卖出24台,卖出的台数与剩
下的台数的比是3︰5。这批洗衣机共有多少台?
按比例分配
知识要点2
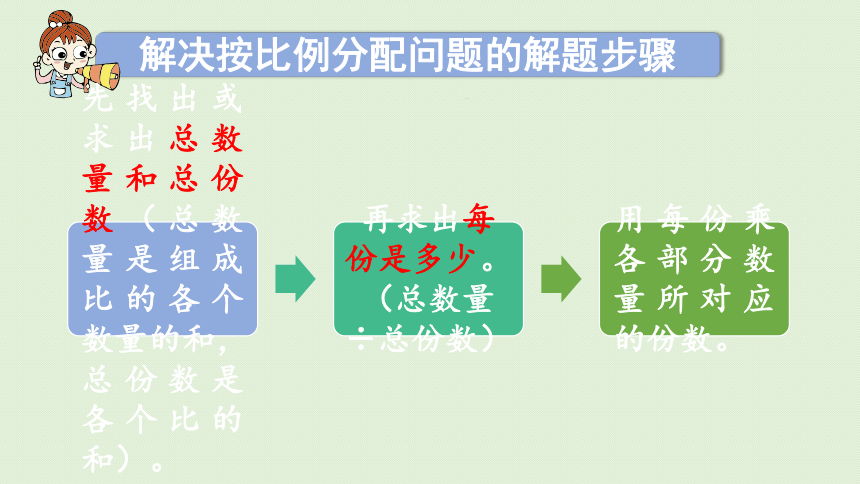
本题是按比例分配问题,该如何解决按比分配问题呢?
解决按比例分配问题的解题步骤
2.商店运来一批洗衣机,卖出24台,卖出的台数与剩下
的台数的比是3︰5。这批洗衣机共有多少台?
把这批洗衣机平均分成8份,卖出的台数占其中的3份。
24÷3×(3+5)=64(台)
答:这批洗衣机共有64台。
解比例
知识要点3
3.解比例。
40 ∶ 2 = 60 ∶x
=
运用比例的基本性质来解比例。
在比例里,两个外项的积等于两个内项的积。
解:
40×x=2×60
40x=120
x=3
解:
80×x=4×100
80x=400
x=5
正比例、反比例的应用
知识要点4
4.北京到济南高速公路距离大约为430 km,北京
到天津大约为120 km。一辆汽车从北京出发开
往济南,当行驶到天津时用了1.5时。按照这个
速度,北京到济南全程需要多少时?
根据问题中的不变量找出两种相关联的量,并正确判断这两种相关联的量成什么比例关系,并根据正、反比例关系式列出相应的方程并求解。
用正(反)比例方法解决问题的步骤
(1)分析题意,判断两种量是否成正(反)比例;
(2)再找出比例式所需的等量关系,并设所求未
知数为x;
(3)解比例。
答:北京到济南全程需要5.375时。
解:设北京到济南全程需要x时。
120
4.北京到济南高速公路距离大约为430 km,北京
到天津大约为120 km。一辆汽车从北京出发开
往济南,当行驶到天津时用了1.5时。按照这个
速度,北京到济南全程需要多少时?
5.学校计划用方砖铺微机室地面,如果用边长5分米的
方砖,需要用360块;如果改用边长6分米的方砖,需
要多少块?
解:设改用边长6分米的方砖,需要x块。
6×6×x = 5×5×360
36x = 9000
x= 250
答:需要250块。
每块方砖的面积×块数=地面面积(一定)
用比例尺求实际距离的方法
知识要点5
6.在比例尺是1∶5000000的地图上,量得A地到B地
的距离是4厘米。一辆汽车以每时40千米的速度从
A地开往B地,问几时可以到达?
图上距离
实际距离
=
比例尺
用比例尺求实际距离的方法
实际距离=图上距离÷比例尺
图上距离÷实际距离=比例尺
图上距离
实际距离
=
比例尺
20000000 cm=200 km
答:5时可以到达。
200÷40=5(时)
6.在比例尺是1∶5000000的地图上,量得A地到B地
的距离是4厘米。一辆汽车以每时40千米的速度从
A地开往B地,问几时可以到达?
正比例图像
知识要点6
6. 河南省郑州市至山东省菏泽市国道线长219 km。一辆大巴车上午9时从郑州市出发,开往菏泽市,行驶的时间和路程如下表。
时间(时) 1 2 3 4
路程(km) 50 100 150 200 219
(教材第79页例1)
(1)把表中所对应的点描在方格纸上,再顺次连
起来。
(2)根据图像估计大巴车到达菏泽市的时间。
1 2 3 4 5
路程(km)
时间(时)
250
200
150
100
50
0
(教材第79页例1)
画正比例关系图像的步骤
(1)把表中所对应的点描在方格纸上,再顺次连起来。
1 2 3 4 5
路程(km)
时间(时)
250
200
150
100
50
0
时间(时) 1 2 3 4
路程(km) 50 100 150 200 219
·
·
·
·
(教材第79页例1)
(2)根据图像估计大巴车到达菏泽市的时间。
大巴车到达菏泽市的时间是13时多。
1 2 3 4 5
路程(km)
时间(时)
250
200
150
100
50
0
·
·
·
·
(教材第79页例1)
课堂练习
1.填空。
(教材第80页练习二十第1题)
(1)把2 g盐放入100 g水中,盐和水的比是( ),
盐和盐水的比是( )。
(2)∶6的比值是( )。如果前项乘4,要使比值
不变,后项应( )。
(3)如果a×5=b×3,那么a∶b=( )∶( );
如果a∶7=b∶9,那么a∶b=( )∶( )。
1∶50
1∶51
乘4
3
5
7
9
2.写出两个比值都是的比,并组成比例。
(教材第80页练习二十第2题)
6∶10=
12∶20=
6∶10= 12∶20
3.解比例。
(教材第80页练习二十第3题)
9 ∶ 8 = x∶12
=
解:
8×x=9×12
8x=108
x=13.5
解:
0.1×x=0.4×35
0.1x=14
x=140
∶ = x∶
×x=×
x=
x=
解:
8x÷8=108÷8
0.1x÷0.1=14÷0.1
x ×8 = ×8
4. 判断每组的两个量是否成比例。如果成比例,
是成什么比例?
(教材第81页练习二十第6题)
(1)生产一批化肥,每天生产吨数与需要时间。
每天生产吨数(吨) 50 100 200 …
需要时间(天) 80 40 20 …
成反比例
=400
×
=400
×
=400
×
(2)圆的半径与直径。
成正比例
1 2 3 4
直径(cm)
半径(cm)
8
7
6
5
4
3
2
1
0
·
·
·
·
(教材第81页练习二十第6题)
(3)某种股票在不同时间的价格变化。
不成比例
(教材第81页练习二十第6题)
5.小东家有1套120 m2的旧房要卖,每平方米可卖
3000元。如果将卖旧房的钱再添4万元去买1套
每平方米5000元的新房,能买多少平方米?
(教材第82页练习二十第7题)
4万元=40000元
解:设能买x m2 。
5000x -40000=3000×120
x=80
答:能买80 m2。
5000x -40000+ 40000 =360000+ 40000
5000x =400000
5000x÷5000 =400000÷5000
6.用水泥、河砂和石子按2∶3∶5 的比例配制240 吨
混凝土,需水泥、河砂和石子各多少吨?
(教材第82页练习二十第9题)
三种原料的总份数:2+3+5=10(份)
每份质量:240÷10=24(吨)
水泥:24×2=48(吨)
河砂:24×3=72(吨)
石子:24×5=120(吨)
答:需水泥48吨,河砂72吨,石子120吨。
7.一个教育考察团到新苗小学参观,该校准备在六年级
选派40 名同学与考察团交流,请按比例确定各班应
选派的人数。
(教材第82页练习二十第10题)
班级 1班 2班 3班 4班
人数(人) 40 44 36 40
选派人数(人)
先要求出4个班的人数比。
40∶44∶36∶40=10∶11∶9∶10
10+11+9+10=40(份)
1班:40×=10(人)
2班:40×=11(人)
3班:40×=9(人)
4班:40×=10(人)
班级 1班 2班 3班 4班
人数(人) 40 44 36 40
选派人数(人)
10
11
9
10
8.一个车间男女工人人数比是4∶5,男性工人比
女性工人少20 人。这个车间共有工人多少人?
(教材第82页练习二十第12题)
男女工人人数比是4∶5,所以把男性工人看作4份,女性工人看作5份。
男性工人比女性工人少5-4=1(份),少20人。
可以求出1份代表20人。
总人数:20×(5+4)=180(人)
作业课件中的相关练习。
02
01
练习二十。
课后作业
第5课时 比和比例
总复习
五
西师版数学六年级(下)
1.进一步掌握比与比例的意义和基本性质,能正确熟练地化简比和求比值。
2.进一步理解正比例和反比例的意义,并能正确判断两种相关联的量成什么比例关系,并能解决简单的实际问题。
3.进一步掌握比例尺的意义,能熟练地应用比例尺的意义解决简单的实际问题。
学习目标
【重点】
掌握比和比例的意义及它们的基本性质,应用
按比例分配和比例尺知识解决问题。
【难点】
正比例和反比例的异同点,优化解决问题
策略。
知识梳理
比和比例
比和比例的 联系与区别
化简比的方法
比值和化简比的区别
化简比 求比值
意义
各部分名称
基本性质
比和比例 的应用
正比例
反比例
比例尺
按比例分配
比
比例
意义
各部分名称
基本性质
两数相除又叫两个数的比。
两个比相等的式子叫做比例。
0.6 0.8 = 0.75
前项
后项
比值
…
…
…
2 : 3 = 6 : 9
内项
外项
比的前项和后项都乘或除以相同的数(0除外)比值不变。
在比例里,两外项之积等于两内项之积。
化简比的依据
解比例的依据
要点回顾
1.把下面各比化成最简单的整数比。
化简比
知识要点1
32∶16
48∶40
0.15∶0.3
∶
运用比的基本性质来化简比。
化简比的方法
整数比
小数比
分数比
比的前项和后项同时除以它们的最大公因数。
把比前、后项的小数点向右移动相同的位数,转化成整数比再化简。
把比前、后项同时乘分母的最小公倍数,转化成整数比再化简。
32∶16
0.15∶0.3
=2∶1
=(32÷16) ∶(16÷16)
=(0.15×100)∶(0.3×100)
=(15÷15)∶ (30 ÷15 )
=15∶30
=1∶2
48∶40
=(48÷8)∶(40÷8)
=6∶5
=(×6 )∶(×6 )
=5∶1
∶
2.商店运来一批洗衣机,卖出24台,卖出的台数与剩
下的台数的比是3︰5。这批洗衣机共有多少台?
按比例分配
知识要点2
本题是按比例分配问题,该如何解决按比分配问题呢?
解决按比例分配问题的解题步骤
2.商店运来一批洗衣机,卖出24台,卖出的台数与剩下
的台数的比是3︰5。这批洗衣机共有多少台?
把这批洗衣机平均分成8份,卖出的台数占其中的3份。
24÷3×(3+5)=64(台)
答:这批洗衣机共有64台。
解比例
知识要点3
3.解比例。
40 ∶ 2 = 60 ∶x
=
运用比例的基本性质来解比例。
在比例里,两个外项的积等于两个内项的积。
解:
40×x=2×60
40x=120
x=3
解:
80×x=4×100
80x=400
x=5
正比例、反比例的应用
知识要点4
4.北京到济南高速公路距离大约为430 km,北京
到天津大约为120 km。一辆汽车从北京出发开
往济南,当行驶到天津时用了1.5时。按照这个
速度,北京到济南全程需要多少时?
根据问题中的不变量找出两种相关联的量,并正确判断这两种相关联的量成什么比例关系,并根据正、反比例关系式列出相应的方程并求解。
用正(反)比例方法解决问题的步骤
(1)分析题意,判断两种量是否成正(反)比例;
(2)再找出比例式所需的等量关系,并设所求未
知数为x;
(3)解比例。
答:北京到济南全程需要5.375时。
解:设北京到济南全程需要x时。
120
4.北京到济南高速公路距离大约为430 km,北京
到天津大约为120 km。一辆汽车从北京出发开
往济南,当行驶到天津时用了1.5时。按照这个
速度,北京到济南全程需要多少时?
5.学校计划用方砖铺微机室地面,如果用边长5分米的
方砖,需要用360块;如果改用边长6分米的方砖,需
要多少块?
解:设改用边长6分米的方砖,需要x块。
6×6×x = 5×5×360
36x = 9000
x= 250
答:需要250块。
每块方砖的面积×块数=地面面积(一定)
用比例尺求实际距离的方法
知识要点5
6.在比例尺是1∶5000000的地图上,量得A地到B地
的距离是4厘米。一辆汽车以每时40千米的速度从
A地开往B地,问几时可以到达?
图上距离
实际距离
=
比例尺
用比例尺求实际距离的方法
实际距离=图上距离÷比例尺
图上距离÷实际距离=比例尺
图上距离
实际距离
=
比例尺
20000000 cm=200 km
答:5时可以到达。
200÷40=5(时)
6.在比例尺是1∶5000000的地图上,量得A地到B地
的距离是4厘米。一辆汽车以每时40千米的速度从
A地开往B地,问几时可以到达?
正比例图像
知识要点6
6. 河南省郑州市至山东省菏泽市国道线长219 km。一辆大巴车上午9时从郑州市出发,开往菏泽市,行驶的时间和路程如下表。
时间(时) 1 2 3 4
路程(km) 50 100 150 200 219
(教材第79页例1)
(1)把表中所对应的点描在方格纸上,再顺次连
起来。
(2)根据图像估计大巴车到达菏泽市的时间。
1 2 3 4 5
路程(km)
时间(时)
250
200
150
100
50
0
(教材第79页例1)
画正比例关系图像的步骤
(1)把表中所对应的点描在方格纸上,再顺次连起来。
1 2 3 4 5
路程(km)
时间(时)
250
200
150
100
50
0
时间(时) 1 2 3 4
路程(km) 50 100 150 200 219
·
·
·
·
(教材第79页例1)
(2)根据图像估计大巴车到达菏泽市的时间。
大巴车到达菏泽市的时间是13时多。
1 2 3 4 5
路程(km)
时间(时)
250
200
150
100
50
0
·
·
·
·
(教材第79页例1)
课堂练习
1.填空。
(教材第80页练习二十第1题)
(1)把2 g盐放入100 g水中,盐和水的比是( ),
盐和盐水的比是( )。
(2)∶6的比值是( )。如果前项乘4,要使比值
不变,后项应( )。
(3)如果a×5=b×3,那么a∶b=( )∶( );
如果a∶7=b∶9,那么a∶b=( )∶( )。
1∶50
1∶51
乘4
3
5
7
9
2.写出两个比值都是的比,并组成比例。
(教材第80页练习二十第2题)
6∶10=
12∶20=
6∶10= 12∶20
3.解比例。
(教材第80页练习二十第3题)
9 ∶ 8 = x∶12
=
解:
8×x=9×12
8x=108
x=13.5
解:
0.1×x=0.4×35
0.1x=14
x=140
∶ = x∶
×x=×
x=
x=
解:
8x÷8=108÷8
0.1x÷0.1=14÷0.1
x ×8 = ×8
4. 判断每组的两个量是否成比例。如果成比例,
是成什么比例?
(教材第81页练习二十第6题)
(1)生产一批化肥,每天生产吨数与需要时间。
每天生产吨数(吨) 50 100 200 …
需要时间(天) 80 40 20 …
成反比例
=400
×
=400
×
=400
×
(2)圆的半径与直径。
成正比例
1 2 3 4
直径(cm)
半径(cm)
8
7
6
5
4
3
2
1
0
·
·
·
·
(教材第81页练习二十第6题)
(3)某种股票在不同时间的价格变化。
不成比例
(教材第81页练习二十第6题)
5.小东家有1套120 m2的旧房要卖,每平方米可卖
3000元。如果将卖旧房的钱再添4万元去买1套
每平方米5000元的新房,能买多少平方米?
(教材第82页练习二十第7题)
4万元=40000元
解:设能买x m2 。
5000x -40000=3000×120
x=80
答:能买80 m2。
5000x -40000+ 40000 =360000+ 40000
5000x =400000
5000x÷5000 =400000÷5000
6.用水泥、河砂和石子按2∶3∶5 的比例配制240 吨
混凝土,需水泥、河砂和石子各多少吨?
(教材第82页练习二十第9题)
三种原料的总份数:2+3+5=10(份)
每份质量:240÷10=24(吨)
水泥:24×2=48(吨)
河砂:24×3=72(吨)
石子:24×5=120(吨)
答:需水泥48吨,河砂72吨,石子120吨。
7.一个教育考察团到新苗小学参观,该校准备在六年级
选派40 名同学与考察团交流,请按比例确定各班应
选派的人数。
(教材第82页练习二十第10题)
班级 1班 2班 3班 4班
人数(人) 40 44 36 40
选派人数(人)
先要求出4个班的人数比。
40∶44∶36∶40=10∶11∶9∶10
10+11+9+10=40(份)
1班:40×=10(人)
2班:40×=11(人)
3班:40×=9(人)
4班:40×=10(人)
班级 1班 2班 3班 4班
人数(人) 40 44 36 40
选派人数(人)
10
11
9
10
8.一个车间男女工人人数比是4∶5,男性工人比
女性工人少20 人。这个车间共有工人多少人?
(教材第82页练习二十第12题)
男女工人人数比是4∶5,所以把男性工人看作4份,女性工人看作5份。
男性工人比女性工人少5-4=1(份),少20人。
可以求出1份代表20人。
总人数:20×(5+4)=180(人)
作业课件中的相关练习。
02
01
练习二十。
课后作业
