2021-2022学年人教版八年级数学上册13.3等腰三角形 填空题专题训练(word版、含解析)
文档属性
| 名称 | 2021-2022学年人教版八年级数学上册13.3等腰三角形 填空题专题训练(word版、含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 406.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-01 14:59:20 | ||
图片预览



文档简介
2021-2022学年人教版八年级数学上册《13.3等腰三角形》填空题专题训练(附答案)
一、填空题
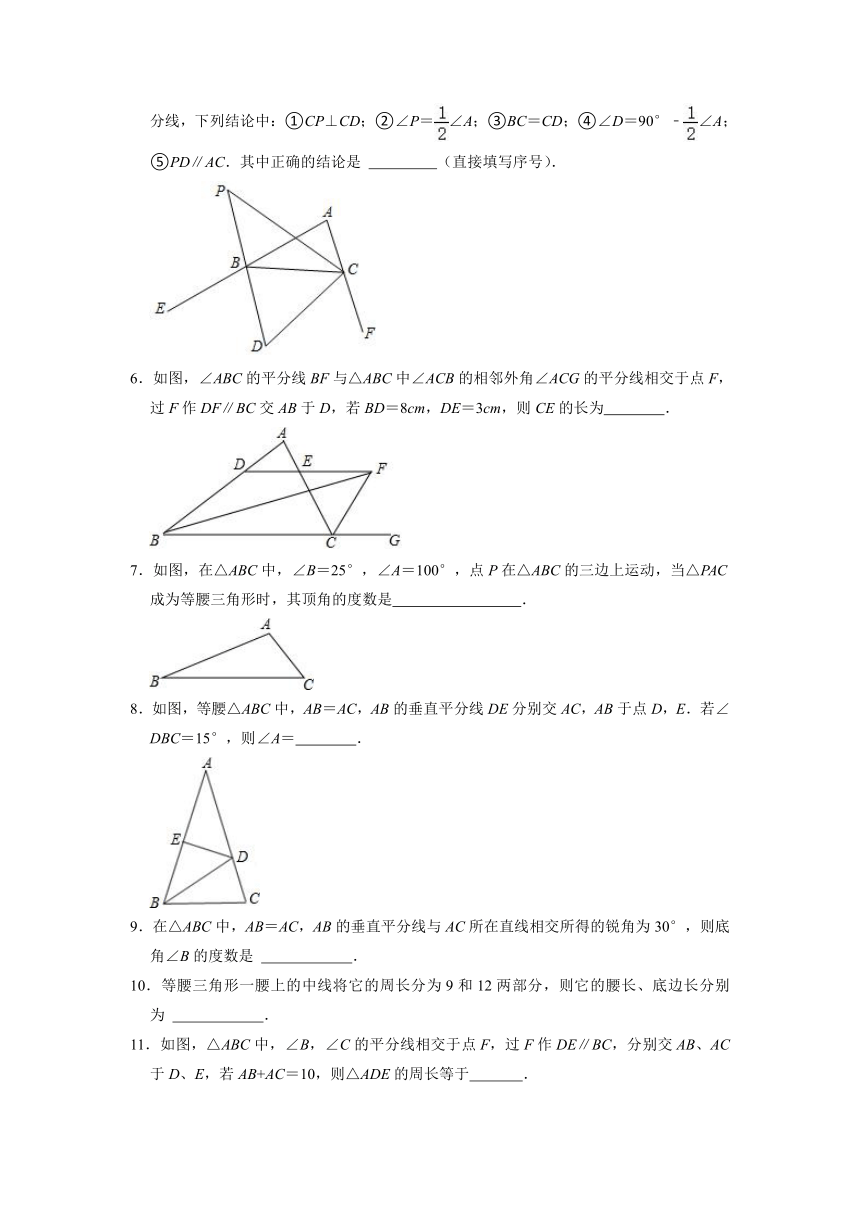
1.如图,BD是△ABC的内角平分线,CE是△ABC的外角平分线,过A分别作AF⊥BD、AG⊥CE,垂足分别为F、G,连接FG,若AB=6,AC=5,BC=4,则FG的长度为 .
2.如图,△ABC中,AD平分∠BAC,∠ACB=3∠B,CE⊥AD,AC=8,BC=BD,则CE= .
3.如图,在△ABC中,AB=AC,以点B为圆心,BC长为半径画弧交AC于点C和点D,再分别以点C和点D为圆心,大于DC长为半径画弧,两弧相交于点F,作射线BF交AC于点E.若∠A=40°,则∠EBC= 度.
4.如图,在△ABC中,AB=AC,∠B=35°,D是BC边上的动点,连接AD,若△ABD为直角三角形,则∠DAC的度数为 .
5.如图,△ABC中,∠A=∠ACB,CP平分∠ACB,BD,CD分别是△ABC的两外角的平分线,下列结论中:①CP⊥CD;②∠P=∠A;③BC=CD;④∠D=90°﹣∠A;⑤PD∥AC.其中正确的结论是 (直接填写序号).
6.如图,∠ABC的平分线BF与△ABC中∠ACB的相邻外角∠ACG的平分线相交于点F,过F作DF∥BC交AB于D,若BD=8cm,DE=3cm,则CE的长为 .
7.如图,在△ABC中,∠B=25°,∠A=100°,点P在△ABC的三边上运动,当△PAC成为等腰三角形时,其顶角的度数是 .
8.如图,等腰△ABC中,AB=AC,AB的垂直平分线DE分别交AC,AB于点D,E.若∠DBC=15°,则∠A= .
9.在△ABC中,AB=AC,AB的垂直平分线与AC所在直线相交所得的锐角为30°,则底角∠B的度数是 .
10.等腰三角形一腰上的中线将它的周长分为9和12两部分,则它的腰长、底边长分别为 .
11.如图,△ABC中,∠B,∠C的平分线相交于点F,过F作DE∥BC,分别交AB、AC于D、E,若AB+AC=10,则△ADE的周长等于 .
如图△ABC面积为6cm2,AP垂直∠ABC平分线BP于点P,则△PBC的面积是 cm2.
13.如图,在△ABC中,AB=AC,D、E分别为AB、AC上的点,∠BDE、∠CED的平分线分别交BC于点F、G,EG∥AB.若∠A=38°,则∠BFD的度数为 .
14.如图,△ABC中,AB=8,AC=2,∠BAC的外角平分线交BC延长线于点E,BD⊥AE于D,若AE=AC,则AD的长为 .
15.如图,在△ABA1中,∠B=28°,AB=A1B,在A1B上取一点C,延长AA1到A2,使得A1A2=A1C,连接A2C.完成下列问题:
(1)∠A1A2C的度数等于 度;
(2)如果继续在A2C上取一点D,延长A1A2到A3,使得A2A3=A2D,连接A3D,…,依此进行下去,那么以An为顶点的锐角的度数等于 度.
16.如图,在△ABC中,AB=AC,AD平分∠BAC,PD垂直平分AB,连接BD并延长,交边AC于点E.若△BCE是等腰三角形,则∠BAC的度数为 .
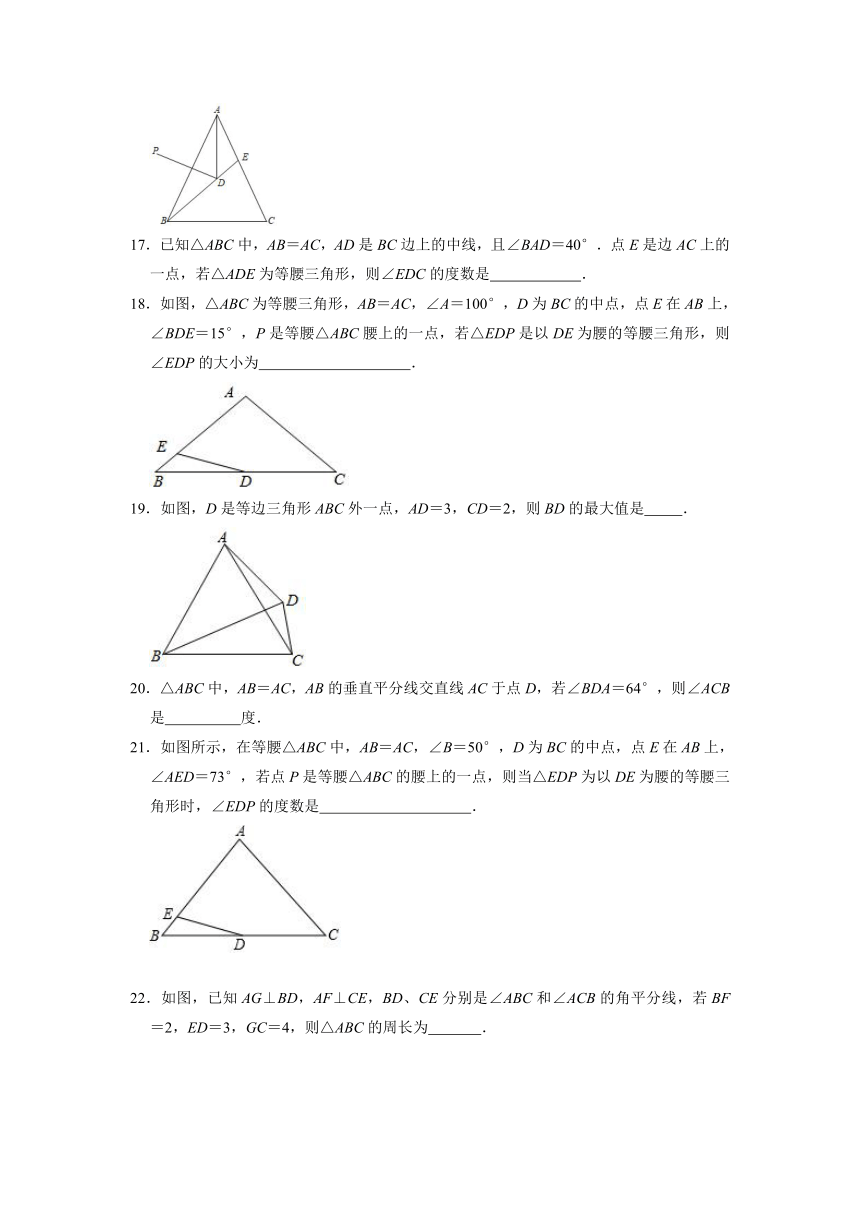
17.已知△ABC中,AB=AC,AD是BC边上的中线,且∠BAD=40°.点E是边AC上的一点,若△ADE为等腰三角形,则∠EDC的度数是 .
18.如图,△ABC为等腰三角形,AB=AC,∠A=100°,D为BC的中点,点E在AB上,∠BDE=15°,P是等腰△ABC腰上的一点,若△EDP是以DE为腰的等腰三角形,则∠EDP的大小为 .
19.如图,D是等边三角形ABC外一点,AD=3,CD=2,则BD的最大值是 .
20.△ABC中,AB=AC,AB的垂直平分线交直线AC于点D,若∠BDA=64°,则∠ACB是 度.
21.如图所示,在等腰△ABC中,AB=AC,∠B=50°,D为BC的中点,点E在AB上,∠AED=73°,若点P是等腰△ABC的腰上的一点,则当△EDP为以DE为腰的等腰三角形时,∠EDP的度数是 .
22.如图,已知AG⊥BD,AF⊥CE,BD、CE分别是∠ABC和∠ACB的角平分线,若BF=2,ED=3,GC=4,则△ABC的周长为 .
23.已知a、b、c是△ABC的三边的长,且满足a2+2b2+c2﹣2b(a+c)=0,则此三角形的形状为 .
24.如图,已知点P是射线BM上一动点(P不与B重合),∠AOB=30°,∠ABM=60°,当∠OAP= 时,以A、O、B中的任意两点和P点为顶点的三角形是等腰三角形.
25.已知a,b,c为△ABC的三边长.b,c满足(b﹣2)2+|c﹣3|=0,且a为方程|x﹣4|=2的解,则△ABC的形状为 三角形.
26.如图,在△ABC中,高AD和BE交于点H,且BH=AC,则∠ABC= .
27.如图,在△ABC中,AB=AC,∠A=40°,AB的垂直平分线MN交AC于点D,则∠DBC= 度.
参考答案
1.解:延长AF交BC于H,延长AG交BC于Q,如图,
∵BD平分∠ABC,
∴∠HBF=∠ABF,
∵AF⊥BD,
∴∠AFB=∠HFB=90°,
∴∠BHA=∠BAH,
∴AB=BH=6,AF=FH,
同理,AC=CQ=5,AG=QG,
∴CH=BH﹣BC=6﹣4=2,
∴HQ=CQ﹣CH=5﹣2=3,
∵AF=FH,AG=QG,
∴FG是△AHQ的中位线,
∴FG=HQ=,
故答案为:.
2.解:延长CE交AB于F,过点D作DH⊥AB于H,DN⊥AC于N,过点A作AM⊥BC于M,如图所示:
∵CE⊥AD,
∴∠AEF=∠AEC=90°,
∵AD平分∠BAC,
∴∠FAE=∠CAE,DH=DN,
在△AEF与△AEC中,,
∴△AEF≌△AEC(ASA),
∴AF=AC=8,∠AFE=∠ACE,EF=CE,
∵∠AFC=∠B+∠ECD,
∴∠ACF=∠B+∠ECD,
∴∠ACB=2∠ECD+∠B,
∵∠ACB=3∠B,
∴2∠ECD+∠B=3∠B,
∴∠B=∠ECD,
∴CF=BF,
∵BC=BD,
∴=,
S△ADB=DH AB=AM BD,S△ACD=DN AC=AM CD,
∴=,
即==,
∴AB=AC=,
∴CF=BF=﹣8=,
∴CE=CF=,
故答案为:.
3.解:∵AB=AC,∠A=40°,
∴∠ACB=(180°﹣40°)÷2=70°,
由题意可知,BC=BD,
∴∠BDC=∠ACB=70°,
∴∠CBD=180°﹣70°×2=40°,
由题意可知,BF平分∠DBC,
∴∠EBC=∠CBD=20°.
故答案为:20.
4.解:如图,∵AB=AC,∠B=35°,
∴∠B=∠C=35°,
∴∠BAC=110°,
当∠BAD=90°时,
∠DAC=110°﹣90°=20°;
当∠ADB=90°时,
∵AB=AC,AD⊥BC,
∴∠DAC=∠BAD=55°.
故答案为:20°或55°.
5.解:∵CP平分∠ACB,CD平分∠BCF,
∴∠PCB=ACB,∠BCD=BCF,
∵∠ACB+∠BCF=180°,
∴∠PCD=∠PCB+∠BCD=ACB+=(∠ACB+∠BCF)=90°,
∴CP⊥CD;故①正确;
延长CB,
∵BD平分∠CBE,∠CBE=∠ABH,
∴BP平分∠ABH,
∴∠PBH=∠BCP+∠P,
∵∠A+2∠PCB=2∠PBH,
∴∠A+2∠PCB=2∠BCP+2∠P,
∴∠A=2∠P,
即:∠P=∠A,故②正确;
假设BC=CD,
∴∠CBD=∠D,
∵∠EBD=∠CBD,
∴∠EBD=∠D,
∴AB∥CD,
∴∠DCF=∠A,
∵∠ACB=∠A,CD平分∠BCF,
∴∠ACB=∠BCD=∠DCF,
∴∠A=∠ACB=60°,
∴△ABC是等边三角形,
而△ABC中,∠A=∠ACB,
∴△ABC是等腰三角形,
∴假设不成立,故③错误;
∵BD、CD分别是△ABC的两个外角∠EBC、∠FCB的平分线,
∴∠EBD=∠DBC,∠BCD=∠DCF,
∴∠DBC+∠DCB+∠D=180°,
∴∠A+∠ABC+∠ACB=180°,
而∠ABC=180°﹣2∠DBC,
∠ACB=180°﹣2∠DCB,
∴∠A+180°﹣2∠DBC+180°﹣2∠DCB=180°,
∴∠A﹣2(∠DBC+∠DCB)=﹣180°,
∴∠A﹣2(180°﹣∠D)=﹣180°,
∴∠A﹣2∠D=180°,
∴∠D=90°﹣∠A,故④正确;
∵∠EBC=∠A+∠ACB,∠A=∠ACB,
∴∠A=∠EBC,
∵∠EBD=EBC,
∴∠EBD=∠A,
∴PD∥AC.故⑤正确;
故答案为:①②④⑤.
6.解:∵BF平分∠ABC,
∴∠ABF=∠CBF,
∵DF∥BC,
∴∠DFB=∠CBF,
∴∠ABF=∠DFB,
∴BD=DF=8cm,
同理,CE=EF,
∵EF=DF﹣DE=5cm,
∴CE=5cm,
故答案为:5cm.
7.解:①如图1,点P在AB上时,AP=AC,顶角为∠A=100°,
②∵∠B=25°,∠A=100°,
∴∠C=180°﹣25°﹣100°=55°,
如图2,点P在BC上时,若AC=PC,顶角为∠C=55°,
如图3,若AC=AP,则顶角为∠CAP=180°﹣2∠C=180°﹣2×55°=70°,
综上所述,顶角为100°或55°或70°.
故答案为:100°或55°或70°.
8.解:设∠A=x,
∵DE垂直平分线AB,
∴AD=BD,
∴∠ABD=∠A=x,
∴∠ABC=15°+x,
∵AB=AC,
∴∠C=∠ABC=15°+x,
在△ABC中,根据三角形内角和等于180°得,
15°+x+15°+x+x=180°,
解得x=50°.
故答案为:50°.
9.解:当△ABC为锐角三角形时,
如图1,设AB的垂直平分线交线段AC于点D,交AB于点E,
∵∠ADE=30°,DE⊥AB,
∴∠A=90°﹣30°=60°,
∵AB=AC,
∴∠B=∠ACB=(180°﹣∠A)=60°;
当△ABC为钝角三角形时,
如图2,设AB的垂直平分线交AB于点E,交AC于点D,
∵∠ADE=30°,DE⊥AB,
∴∠DAB=60°,
∵AB=AC,
∴∠B=∠C,
∵∠B+∠C=∠DAB,
∴∠B=30°;
综上可知∠B的度数为60°或30°,
故答案为:60°或30°.
10.解:设等腰三角形的腰长为2x,
由题意得2x+x=9或2x+x=12,
解得x=3或4,
∴等腰三角形的腰长为6或8,
∵等腰三角形的周长为9+12=21,
∴该等腰三角形的底边长为:21﹣2×6=9或21﹣2×8=5,
∵6+6=12>9,5+8>8,
∴等腰三角形的腰长,底边长分别为:6,9或8,5.
故答案为6,9或8,5.
11.解:∵BF平分∠ABC,
∴∠DBF=∠CBF,
∵DE∥BC,
∴∠CBF=∠DFB,
∴∠DBF=∠DFB,
∴BD=DF,
同理FE=EC,
∴△ADE的周长=AD+AE+ED=AD+DF+AE+EF=(AD+BD)+(AE+CE)=AB+AC=10,
故答案为:10.
12.解:延长AP交BC于点E,如图所示.
∵AP垂直∠ABC的平分线BP于点P,
∴∠ABP=∠EBP.
在△ABP和△EBP中,
,
∴△ABP≌△EBP(ASA),
∴AP=EP.
∵△APC和△EPC等底同高,
∴S△APC=S△CPE,
∴S△PBC=S△BPE+S△CPE=S△ABC=×6=3(cm2),
故答案为:3.
13.解:∵AB=AC,∠A=38°,
∴∠B=∠C=(180°﹣38°)=71°,
∵EG平分∠DEC,
∴∠CEG=∠DEG,
∵EG∥AB,
∴∠CEG=∠A,∠GED=∠ADE,
∴∠A=∠EDA=38°,
∵FD平分∠BDE,
∴∠BDF=∠FDE=71°,
∴∠BFD=180﹣71°﹣71°=38°,
故答案为:38°.
14.解:延长AD至点G,使DG=AD,连接BG,延长BA至F,
∵BD垂直平分AG,
∴BA=BG=8,
∠BAG=∠G
∵∠BAG=∠EAF,∠BAC的外角平分线交BC延长线于点E,
∴∠EAF=∠G,∠CAE=∠EAF,
∴∠G=∠CAE,
∴AC∥GB,
∴∠ACE=∠GBE,
∵AE=AC=2,
∴∠ACE=∠E,
∴∠GBE=∠E,
∴GB=GE=8,
∵DG+AD=GE﹣AE,
∴2AD=6,
∴AD=3.
故答案为3.
15.解:(1)在△ABA1中,∠B=28°,AB=A1B,
∴∠BA1A===76°,
∵A1A2=A1C,∠BA1A是△A1A2C的外角,
∴∠A1A2C=∠BA1A=×76°=38°;
(2)同理可得,∠DA3A2=19°,∠EA4A3=9.5°,
∴以An为顶点的锐角的度数等于度.
故答案为:38,.
16.解:∵AD平分∠BAC,
∴∠BAD=∠CAD=α,
∵AB=AC,
∴∠ABC=∠C==90°﹣α,
∵PD垂直平分AB,
∴AD=BD,
∴∠ABD=∠BAD=α,
∠EBC=∠ABC﹣∠ABE=90°﹣2α,
∴∠BEC=∠ABE+∠BAC=3α,
当BE=BC时,
∠BEC=∠C,即90°﹣α=3α,
解得α=22.5°,
∴∠BAC=2α=45°;
当BE=CE时,
∠EBC=∠C,此时点E和点A重合,舍去;
当CE=BC时,
∠BEC=∠EBC,即90°﹣2α=3α,
解得α=18°,
∴∠BAC=2α=36°.
故∠BAC的度数为45°或36°.
故答案为:45°或36°.
17.解:∵AB=AC,AD是BC边上的中线,且∠BAD=40°,
∴∠CAD=∠BAD=40°,∠ADC=90°,
①AE1=DE1时,
∠ADE1=∠CAD=40°,
则∠E1DC=90°﹣40°=50°;
②AE2=AD时,
∠ADE2=∠AE2D=(180°﹣40°)÷2=70°,
则∠E2DC=90°﹣70°=20°.
故∠EDC的度数是50°或20°.
故答案为:50°或20°.
18.解:∵AB=AC,∠A=100°,
∴∠B=(180°﹣∠A)=40°,
∵∠BDE=15°,
∴∠AED=55°,
∵当△DEP是以DE为腰的等腰三角形,
①当点P在AB上,
∵DE=DP1,
∴∠DP1E=∠AED=55°,
∴∠EDP1=180°﹣55°﹣55°=70°,
②当点P在AC上,
∵AB=AC,D为BC的中点,
∴∠BAD=∠CAD,
过D作DG⊥AB于G,DH⊥AC于H,
∴DG=DH,
在Rt△DEG与Rt△DP2H中,
,
∴Rt△DEG≌Rt△DP2H(HL),
∴∠AP2D=∠AED=55°,
∵∠BAC=100°,
∴∠EDP2=150°,
③当点P在AC上,
同理证得Rt△DEG≌Rt△DPH(HL),
∴∠EDG=∠P3DH,
∴∠EDP3=∠GDH=180°﹣100°=80°,
④当点P在AB上,EP=ED时,∠EDP=(180°﹣55°)=62.5°.
故答案为:62.5°或70°或80°或150°.
19.解:以CD为边作等边△DCE,连接AE.
∵BC=AC,CD=CE,∠BCA=∠DCE=60°,
∴∠BCD=∠ACE,
在△BCD和△ACE中,
∴△BCD≌△ACE(SAS),
∴BD=AE,
在△ADE中,
∵AD=3,DE=CD=2,
∴AE≤AD+DE,
∴AE≤5,
∴AE的最大值为5,
∴BD的最大值为5.
故答案为:5.
20.解:如图1,∵DE垂直平分AB,
∴AD=BD,
∴∠BAC=∠ABD,
∵∠BDA=64°,
∴∠BAC=∠ABD=58°,
∴∠ACB=61°;
如图2,∵DE垂直平分AB,
∴AD=BD,
∴∠BAD=∠ABD,
∵∠BDA=64°,
∴∠BAD=∠ABD=58°,
∴∠BAC=122°,
∴∠ACB=29°.
故∠ACB是61或29度.
故答案为:61或29.
21.解:∵AB=AC,∠B=50°,∠AED=73°,
∴∠EDB=23°,
∵当△DEP是以DE为腰的等腰三角形,
①当点P在AB上,
∵DE=DP1,
∴∠DP1E=∠AED=73°,
∴∠EDP1=180°﹣73°﹣73°=34°,
②当点P在AC上,
∵AB=AC,D为BC的中点,
∴∠BAD=∠CAD,
过D作DG⊥AB于G,DH⊥AC于H,
∴DG=DH,
在Rt△DEG与Rt△DP2H中,,
∴Rt△DEG≌Rt△DP2H(HL),
∴∠AP2D=∠AED=73°,
∵∠BAC=180°﹣50°﹣50°=80°,
∴∠EDP2=134°,
③当点P在AC上,
同理证得Rt△DEG≌Rt△DPH(HL),
∴∠EDG=∠P3DH,
∴∠EDP3=∠GDH=180°﹣80°=100°,
④当点P在AB上,EP=ED时,∠EDP=(180°﹣73°)=53.5°.
故答案为:34°或53.5°或100°或134°.
22.解:由AG⊥BD,BD是∠ABC的平分线,
可得∠ADB=∠GDB=90°,∠ABD=∠GBD,BD为公共边,
∴△ADB≌△GDB,∴AB=GB,
∵AF⊥CE,CE是∠ACB的角平分线,
同理可证;AC=FC,
即△ABG和△ACF都是等腰三角形.
又因AG⊥BD,AF⊥CE,所以E、D分别是AF和AG的中点,
即ED是△AFG的中位线,∴FG=2DE,
则△ABC的周长为:AB+BC+AC=BF+FG+BF+FG+CG+FG+CG
由BF=2,ED=3,GC=4,FG=2DE=6得则△ABC的周长为30.
故答案为:30
23.解:由已知条件a2+2b2+c2﹣2b(a+c)=0化简得,
(a﹣b)2+(b﹣c)2=0
∴a﹣b=0,b﹣c=0
即 a=b,b=c
∴a=b=c
故答案为等边三角形.
24.解:分为以下5种情况:
①OA=OP,
∵∠AOB=30°,OA=OP,
∴∠OAP=∠OPA=(180°﹣30°)=75°;
②OA=AP,
∵∠AOB=30°,OA=AP,
∴∠APO=∠AOB=30°,
∴∠OAP=180°﹣∠AOB﹣∠APO=180°﹣30°﹣30°=120°;
③AB=AP,
∵∠AOM=60°,AB=AP,
∴∠APO=∠ABM=60°,
∴∠OAP=180°﹣∠AOB﹣∠APO=180°﹣30°﹣60°=90°;
④AB=BP,
∵∠ABM=60°,AB=BP,
∴∠BAP=∠APO=(180°﹣60°)=60°,
∴∠OAP=180°﹣∠AOB﹣∠APO=180°﹣30°﹣60°=90°;
⑤AP=BP,
∵∠ABM=60°,AP=BP,
∴∠ABO=∠PAB=60°,
∴∠APO=180°﹣60°﹣60°=60°,
∴∠OAP=180°﹣∠AOB﹣∠APO=180°﹣30°﹣60°=90°;
所以当∠OAP=75°或120°或90°时,以A、O、B中的任意两点和P点为顶点的三角形是等腰三角形,
故答案为:75°或120°或90°.
25.解:∵(b﹣2)2+|c﹣3|=0,
∴b﹣2=0,c﹣3=0,
解得:b=2,c=3,
∵a为方程|x﹣4|=2的解,
∴a﹣4=±2,
解得:a=6或2,
∵a、b、c为△ABC的三边长,b+c<6,
∴a=6不合题意,舍去,
∴a=2,
∴a=b=2,
∴△ABC是等腰三角形,
故答案为:等腰.
26.解:∵△ABC为锐角三角形,
∴高AD和BE在三角形内.
∵高AD和BE交于点H,
∴∠ADC=∠BEC=90°.
∵∠EBD+∠BHD=90°,∠AHE+∠HAE=90°,∠BHD=∠AHE,
∴∠EAD=∠EBD,
又∵BH=AC,∠ADC=∠BDH=90°,
∴△BDH≌△ADC(AAS),
∴BD=AD,
∵∠ADB=90°,
∴∠ABC=45°.
故答案为45°
27.解:∵AB=AC,∠A=40°,
∴∠ABC=(180°﹣∠A)=×(180°﹣40°)=70°,
∵MN垂直平分线AB,
∴AD=BD,
∴∠ABD=∠A=40°,
∴∠DBC=∠ABC﹣∠ABD=70°﹣40°=30°.
故答案为:30.
一、填空题
1.如图,BD是△ABC的内角平分线,CE是△ABC的外角平分线,过A分别作AF⊥BD、AG⊥CE,垂足分别为F、G,连接FG,若AB=6,AC=5,BC=4,则FG的长度为 .
2.如图,△ABC中,AD平分∠BAC,∠ACB=3∠B,CE⊥AD,AC=8,BC=BD,则CE= .
3.如图,在△ABC中,AB=AC,以点B为圆心,BC长为半径画弧交AC于点C和点D,再分别以点C和点D为圆心,大于DC长为半径画弧,两弧相交于点F,作射线BF交AC于点E.若∠A=40°,则∠EBC= 度.
4.如图,在△ABC中,AB=AC,∠B=35°,D是BC边上的动点,连接AD,若△ABD为直角三角形,则∠DAC的度数为 .
5.如图,△ABC中,∠A=∠ACB,CP平分∠ACB,BD,CD分别是△ABC的两外角的平分线,下列结论中:①CP⊥CD;②∠P=∠A;③BC=CD;④∠D=90°﹣∠A;⑤PD∥AC.其中正确的结论是 (直接填写序号).
6.如图,∠ABC的平分线BF与△ABC中∠ACB的相邻外角∠ACG的平分线相交于点F,过F作DF∥BC交AB于D,若BD=8cm,DE=3cm,则CE的长为 .
7.如图,在△ABC中,∠B=25°,∠A=100°,点P在△ABC的三边上运动,当△PAC成为等腰三角形时,其顶角的度数是 .
8.如图,等腰△ABC中,AB=AC,AB的垂直平分线DE分别交AC,AB于点D,E.若∠DBC=15°,则∠A= .
9.在△ABC中,AB=AC,AB的垂直平分线与AC所在直线相交所得的锐角为30°,则底角∠B的度数是 .
10.等腰三角形一腰上的中线将它的周长分为9和12两部分,则它的腰长、底边长分别为 .
11.如图,△ABC中,∠B,∠C的平分线相交于点F,过F作DE∥BC,分别交AB、AC于D、E,若AB+AC=10,则△ADE的周长等于 .
如图△ABC面积为6cm2,AP垂直∠ABC平分线BP于点P,则△PBC的面积是 cm2.
13.如图,在△ABC中,AB=AC,D、E分别为AB、AC上的点,∠BDE、∠CED的平分线分别交BC于点F、G,EG∥AB.若∠A=38°,则∠BFD的度数为 .
14.如图,△ABC中,AB=8,AC=2,∠BAC的外角平分线交BC延长线于点E,BD⊥AE于D,若AE=AC,则AD的长为 .
15.如图,在△ABA1中,∠B=28°,AB=A1B,在A1B上取一点C,延长AA1到A2,使得A1A2=A1C,连接A2C.完成下列问题:
(1)∠A1A2C的度数等于 度;
(2)如果继续在A2C上取一点D,延长A1A2到A3,使得A2A3=A2D,连接A3D,…,依此进行下去,那么以An为顶点的锐角的度数等于 度.
16.如图,在△ABC中,AB=AC,AD平分∠BAC,PD垂直平分AB,连接BD并延长,交边AC于点E.若△BCE是等腰三角形,则∠BAC的度数为 .
17.已知△ABC中,AB=AC,AD是BC边上的中线,且∠BAD=40°.点E是边AC上的一点,若△ADE为等腰三角形,则∠EDC的度数是 .
18.如图,△ABC为等腰三角形,AB=AC,∠A=100°,D为BC的中点,点E在AB上,∠BDE=15°,P是等腰△ABC腰上的一点,若△EDP是以DE为腰的等腰三角形,则∠EDP的大小为 .
19.如图,D是等边三角形ABC外一点,AD=3,CD=2,则BD的最大值是 .
20.△ABC中,AB=AC,AB的垂直平分线交直线AC于点D,若∠BDA=64°,则∠ACB是 度.
21.如图所示,在等腰△ABC中,AB=AC,∠B=50°,D为BC的中点,点E在AB上,∠AED=73°,若点P是等腰△ABC的腰上的一点,则当△EDP为以DE为腰的等腰三角形时,∠EDP的度数是 .
22.如图,已知AG⊥BD,AF⊥CE,BD、CE分别是∠ABC和∠ACB的角平分线,若BF=2,ED=3,GC=4,则△ABC的周长为 .
23.已知a、b、c是△ABC的三边的长,且满足a2+2b2+c2﹣2b(a+c)=0,则此三角形的形状为 .
24.如图,已知点P是射线BM上一动点(P不与B重合),∠AOB=30°,∠ABM=60°,当∠OAP= 时,以A、O、B中的任意两点和P点为顶点的三角形是等腰三角形.
25.已知a,b,c为△ABC的三边长.b,c满足(b﹣2)2+|c﹣3|=0,且a为方程|x﹣4|=2的解,则△ABC的形状为 三角形.
26.如图,在△ABC中,高AD和BE交于点H,且BH=AC,则∠ABC= .
27.如图,在△ABC中,AB=AC,∠A=40°,AB的垂直平分线MN交AC于点D,则∠DBC= 度.
参考答案
1.解:延长AF交BC于H,延长AG交BC于Q,如图,
∵BD平分∠ABC,
∴∠HBF=∠ABF,
∵AF⊥BD,
∴∠AFB=∠HFB=90°,
∴∠BHA=∠BAH,
∴AB=BH=6,AF=FH,
同理,AC=CQ=5,AG=QG,
∴CH=BH﹣BC=6﹣4=2,
∴HQ=CQ﹣CH=5﹣2=3,
∵AF=FH,AG=QG,
∴FG是△AHQ的中位线,
∴FG=HQ=,
故答案为:.
2.解:延长CE交AB于F,过点D作DH⊥AB于H,DN⊥AC于N,过点A作AM⊥BC于M,如图所示:
∵CE⊥AD,
∴∠AEF=∠AEC=90°,
∵AD平分∠BAC,
∴∠FAE=∠CAE,DH=DN,
在△AEF与△AEC中,,
∴△AEF≌△AEC(ASA),
∴AF=AC=8,∠AFE=∠ACE,EF=CE,
∵∠AFC=∠B+∠ECD,
∴∠ACF=∠B+∠ECD,
∴∠ACB=2∠ECD+∠B,
∵∠ACB=3∠B,
∴2∠ECD+∠B=3∠B,
∴∠B=∠ECD,
∴CF=BF,
∵BC=BD,
∴=,
S△ADB=DH AB=AM BD,S△ACD=DN AC=AM CD,
∴=,
即==,
∴AB=AC=,
∴CF=BF=﹣8=,
∴CE=CF=,
故答案为:.
3.解:∵AB=AC,∠A=40°,
∴∠ACB=(180°﹣40°)÷2=70°,
由题意可知,BC=BD,
∴∠BDC=∠ACB=70°,
∴∠CBD=180°﹣70°×2=40°,
由题意可知,BF平分∠DBC,
∴∠EBC=∠CBD=20°.
故答案为:20.
4.解:如图,∵AB=AC,∠B=35°,
∴∠B=∠C=35°,
∴∠BAC=110°,
当∠BAD=90°时,
∠DAC=110°﹣90°=20°;
当∠ADB=90°时,
∵AB=AC,AD⊥BC,
∴∠DAC=∠BAD=55°.
故答案为:20°或55°.
5.解:∵CP平分∠ACB,CD平分∠BCF,
∴∠PCB=ACB,∠BCD=BCF,
∵∠ACB+∠BCF=180°,
∴∠PCD=∠PCB+∠BCD=ACB+=(∠ACB+∠BCF)=90°,
∴CP⊥CD;故①正确;
延长CB,
∵BD平分∠CBE,∠CBE=∠ABH,
∴BP平分∠ABH,
∴∠PBH=∠BCP+∠P,
∵∠A+2∠PCB=2∠PBH,
∴∠A+2∠PCB=2∠BCP+2∠P,
∴∠A=2∠P,
即:∠P=∠A,故②正确;
假设BC=CD,
∴∠CBD=∠D,
∵∠EBD=∠CBD,
∴∠EBD=∠D,
∴AB∥CD,
∴∠DCF=∠A,
∵∠ACB=∠A,CD平分∠BCF,
∴∠ACB=∠BCD=∠DCF,
∴∠A=∠ACB=60°,
∴△ABC是等边三角形,
而△ABC中,∠A=∠ACB,
∴△ABC是等腰三角形,
∴假设不成立,故③错误;
∵BD、CD分别是△ABC的两个外角∠EBC、∠FCB的平分线,
∴∠EBD=∠DBC,∠BCD=∠DCF,
∴∠DBC+∠DCB+∠D=180°,
∴∠A+∠ABC+∠ACB=180°,
而∠ABC=180°﹣2∠DBC,
∠ACB=180°﹣2∠DCB,
∴∠A+180°﹣2∠DBC+180°﹣2∠DCB=180°,
∴∠A﹣2(∠DBC+∠DCB)=﹣180°,
∴∠A﹣2(180°﹣∠D)=﹣180°,
∴∠A﹣2∠D=180°,
∴∠D=90°﹣∠A,故④正确;
∵∠EBC=∠A+∠ACB,∠A=∠ACB,
∴∠A=∠EBC,
∵∠EBD=EBC,
∴∠EBD=∠A,
∴PD∥AC.故⑤正确;
故答案为:①②④⑤.
6.解:∵BF平分∠ABC,
∴∠ABF=∠CBF,
∵DF∥BC,
∴∠DFB=∠CBF,
∴∠ABF=∠DFB,
∴BD=DF=8cm,
同理,CE=EF,
∵EF=DF﹣DE=5cm,
∴CE=5cm,
故答案为:5cm.
7.解:①如图1,点P在AB上时,AP=AC,顶角为∠A=100°,
②∵∠B=25°,∠A=100°,
∴∠C=180°﹣25°﹣100°=55°,
如图2,点P在BC上时,若AC=PC,顶角为∠C=55°,
如图3,若AC=AP,则顶角为∠CAP=180°﹣2∠C=180°﹣2×55°=70°,
综上所述,顶角为100°或55°或70°.
故答案为:100°或55°或70°.
8.解:设∠A=x,
∵DE垂直平分线AB,
∴AD=BD,
∴∠ABD=∠A=x,
∴∠ABC=15°+x,
∵AB=AC,
∴∠C=∠ABC=15°+x,
在△ABC中,根据三角形内角和等于180°得,
15°+x+15°+x+x=180°,
解得x=50°.
故答案为:50°.
9.解:当△ABC为锐角三角形时,
如图1,设AB的垂直平分线交线段AC于点D,交AB于点E,
∵∠ADE=30°,DE⊥AB,
∴∠A=90°﹣30°=60°,
∵AB=AC,
∴∠B=∠ACB=(180°﹣∠A)=60°;
当△ABC为钝角三角形时,
如图2,设AB的垂直平分线交AB于点E,交AC于点D,
∵∠ADE=30°,DE⊥AB,
∴∠DAB=60°,
∵AB=AC,
∴∠B=∠C,
∵∠B+∠C=∠DAB,
∴∠B=30°;
综上可知∠B的度数为60°或30°,
故答案为:60°或30°.
10.解:设等腰三角形的腰长为2x,
由题意得2x+x=9或2x+x=12,
解得x=3或4,
∴等腰三角形的腰长为6或8,
∵等腰三角形的周长为9+12=21,
∴该等腰三角形的底边长为:21﹣2×6=9或21﹣2×8=5,
∵6+6=12>9,5+8>8,
∴等腰三角形的腰长,底边长分别为:6,9或8,5.
故答案为6,9或8,5.
11.解:∵BF平分∠ABC,
∴∠DBF=∠CBF,
∵DE∥BC,
∴∠CBF=∠DFB,
∴∠DBF=∠DFB,
∴BD=DF,
同理FE=EC,
∴△ADE的周长=AD+AE+ED=AD+DF+AE+EF=(AD+BD)+(AE+CE)=AB+AC=10,
故答案为:10.
12.解:延长AP交BC于点E,如图所示.
∵AP垂直∠ABC的平分线BP于点P,
∴∠ABP=∠EBP.
在△ABP和△EBP中,
,
∴△ABP≌△EBP(ASA),
∴AP=EP.
∵△APC和△EPC等底同高,
∴S△APC=S△CPE,
∴S△PBC=S△BPE+S△CPE=S△ABC=×6=3(cm2),
故答案为:3.
13.解:∵AB=AC,∠A=38°,
∴∠B=∠C=(180°﹣38°)=71°,
∵EG平分∠DEC,
∴∠CEG=∠DEG,
∵EG∥AB,
∴∠CEG=∠A,∠GED=∠ADE,
∴∠A=∠EDA=38°,
∵FD平分∠BDE,
∴∠BDF=∠FDE=71°,
∴∠BFD=180﹣71°﹣71°=38°,
故答案为:38°.
14.解:延长AD至点G,使DG=AD,连接BG,延长BA至F,
∵BD垂直平分AG,
∴BA=BG=8,
∠BAG=∠G
∵∠BAG=∠EAF,∠BAC的外角平分线交BC延长线于点E,
∴∠EAF=∠G,∠CAE=∠EAF,
∴∠G=∠CAE,
∴AC∥GB,
∴∠ACE=∠GBE,
∵AE=AC=2,
∴∠ACE=∠E,
∴∠GBE=∠E,
∴GB=GE=8,
∵DG+AD=GE﹣AE,
∴2AD=6,
∴AD=3.
故答案为3.
15.解:(1)在△ABA1中,∠B=28°,AB=A1B,
∴∠BA1A===76°,
∵A1A2=A1C,∠BA1A是△A1A2C的外角,
∴∠A1A2C=∠BA1A=×76°=38°;
(2)同理可得,∠DA3A2=19°,∠EA4A3=9.5°,
∴以An为顶点的锐角的度数等于度.
故答案为:38,.
16.解:∵AD平分∠BAC,
∴∠BAD=∠CAD=α,
∵AB=AC,
∴∠ABC=∠C==90°﹣α,
∵PD垂直平分AB,
∴AD=BD,
∴∠ABD=∠BAD=α,
∠EBC=∠ABC﹣∠ABE=90°﹣2α,
∴∠BEC=∠ABE+∠BAC=3α,
当BE=BC时,
∠BEC=∠C,即90°﹣α=3α,
解得α=22.5°,
∴∠BAC=2α=45°;
当BE=CE时,
∠EBC=∠C,此时点E和点A重合,舍去;
当CE=BC时,
∠BEC=∠EBC,即90°﹣2α=3α,
解得α=18°,
∴∠BAC=2α=36°.
故∠BAC的度数为45°或36°.
故答案为:45°或36°.
17.解:∵AB=AC,AD是BC边上的中线,且∠BAD=40°,
∴∠CAD=∠BAD=40°,∠ADC=90°,
①AE1=DE1时,
∠ADE1=∠CAD=40°,
则∠E1DC=90°﹣40°=50°;
②AE2=AD时,
∠ADE2=∠AE2D=(180°﹣40°)÷2=70°,
则∠E2DC=90°﹣70°=20°.
故∠EDC的度数是50°或20°.
故答案为:50°或20°.
18.解:∵AB=AC,∠A=100°,
∴∠B=(180°﹣∠A)=40°,
∵∠BDE=15°,
∴∠AED=55°,
∵当△DEP是以DE为腰的等腰三角形,
①当点P在AB上,
∵DE=DP1,
∴∠DP1E=∠AED=55°,
∴∠EDP1=180°﹣55°﹣55°=70°,
②当点P在AC上,
∵AB=AC,D为BC的中点,
∴∠BAD=∠CAD,
过D作DG⊥AB于G,DH⊥AC于H,
∴DG=DH,
在Rt△DEG与Rt△DP2H中,
,
∴Rt△DEG≌Rt△DP2H(HL),
∴∠AP2D=∠AED=55°,
∵∠BAC=100°,
∴∠EDP2=150°,
③当点P在AC上,
同理证得Rt△DEG≌Rt△DPH(HL),
∴∠EDG=∠P3DH,
∴∠EDP3=∠GDH=180°﹣100°=80°,
④当点P在AB上,EP=ED时,∠EDP=(180°﹣55°)=62.5°.
故答案为:62.5°或70°或80°或150°.
19.解:以CD为边作等边△DCE,连接AE.
∵BC=AC,CD=CE,∠BCA=∠DCE=60°,
∴∠BCD=∠ACE,
在△BCD和△ACE中,
∴△BCD≌△ACE(SAS),
∴BD=AE,
在△ADE中,
∵AD=3,DE=CD=2,
∴AE≤AD+DE,
∴AE≤5,
∴AE的最大值为5,
∴BD的最大值为5.
故答案为:5.
20.解:如图1,∵DE垂直平分AB,
∴AD=BD,
∴∠BAC=∠ABD,
∵∠BDA=64°,
∴∠BAC=∠ABD=58°,
∴∠ACB=61°;
如图2,∵DE垂直平分AB,
∴AD=BD,
∴∠BAD=∠ABD,
∵∠BDA=64°,
∴∠BAD=∠ABD=58°,
∴∠BAC=122°,
∴∠ACB=29°.
故∠ACB是61或29度.
故答案为:61或29.
21.解:∵AB=AC,∠B=50°,∠AED=73°,
∴∠EDB=23°,
∵当△DEP是以DE为腰的等腰三角形,
①当点P在AB上,
∵DE=DP1,
∴∠DP1E=∠AED=73°,
∴∠EDP1=180°﹣73°﹣73°=34°,
②当点P在AC上,
∵AB=AC,D为BC的中点,
∴∠BAD=∠CAD,
过D作DG⊥AB于G,DH⊥AC于H,
∴DG=DH,
在Rt△DEG与Rt△DP2H中,,
∴Rt△DEG≌Rt△DP2H(HL),
∴∠AP2D=∠AED=73°,
∵∠BAC=180°﹣50°﹣50°=80°,
∴∠EDP2=134°,
③当点P在AC上,
同理证得Rt△DEG≌Rt△DPH(HL),
∴∠EDG=∠P3DH,
∴∠EDP3=∠GDH=180°﹣80°=100°,
④当点P在AB上,EP=ED时,∠EDP=(180°﹣73°)=53.5°.
故答案为:34°或53.5°或100°或134°.
22.解:由AG⊥BD,BD是∠ABC的平分线,
可得∠ADB=∠GDB=90°,∠ABD=∠GBD,BD为公共边,
∴△ADB≌△GDB,∴AB=GB,
∵AF⊥CE,CE是∠ACB的角平分线,
同理可证;AC=FC,
即△ABG和△ACF都是等腰三角形.
又因AG⊥BD,AF⊥CE,所以E、D分别是AF和AG的中点,
即ED是△AFG的中位线,∴FG=2DE,
则△ABC的周长为:AB+BC+AC=BF+FG+BF+FG+CG+FG+CG
由BF=2,ED=3,GC=4,FG=2DE=6得则△ABC的周长为30.
故答案为:30
23.解:由已知条件a2+2b2+c2﹣2b(a+c)=0化简得,
(a﹣b)2+(b﹣c)2=0
∴a﹣b=0,b﹣c=0
即 a=b,b=c
∴a=b=c
故答案为等边三角形.
24.解:分为以下5种情况:
①OA=OP,
∵∠AOB=30°,OA=OP,
∴∠OAP=∠OPA=(180°﹣30°)=75°;
②OA=AP,
∵∠AOB=30°,OA=AP,
∴∠APO=∠AOB=30°,
∴∠OAP=180°﹣∠AOB﹣∠APO=180°﹣30°﹣30°=120°;
③AB=AP,
∵∠AOM=60°,AB=AP,
∴∠APO=∠ABM=60°,
∴∠OAP=180°﹣∠AOB﹣∠APO=180°﹣30°﹣60°=90°;
④AB=BP,
∵∠ABM=60°,AB=BP,
∴∠BAP=∠APO=(180°﹣60°)=60°,
∴∠OAP=180°﹣∠AOB﹣∠APO=180°﹣30°﹣60°=90°;
⑤AP=BP,
∵∠ABM=60°,AP=BP,
∴∠ABO=∠PAB=60°,
∴∠APO=180°﹣60°﹣60°=60°,
∴∠OAP=180°﹣∠AOB﹣∠APO=180°﹣30°﹣60°=90°;
所以当∠OAP=75°或120°或90°时,以A、O、B中的任意两点和P点为顶点的三角形是等腰三角形,
故答案为:75°或120°或90°.
25.解:∵(b﹣2)2+|c﹣3|=0,
∴b﹣2=0,c﹣3=0,
解得:b=2,c=3,
∵a为方程|x﹣4|=2的解,
∴a﹣4=±2,
解得:a=6或2,
∵a、b、c为△ABC的三边长,b+c<6,
∴a=6不合题意,舍去,
∴a=2,
∴a=b=2,
∴△ABC是等腰三角形,
故答案为:等腰.
26.解:∵△ABC为锐角三角形,
∴高AD和BE在三角形内.
∵高AD和BE交于点H,
∴∠ADC=∠BEC=90°.
∵∠EBD+∠BHD=90°,∠AHE+∠HAE=90°,∠BHD=∠AHE,
∴∠EAD=∠EBD,
又∵BH=AC,∠ADC=∠BDH=90°,
∴△BDH≌△ADC(AAS),
∴BD=AD,
∵∠ADB=90°,
∴∠ABC=45°.
故答案为45°
27.解:∵AB=AC,∠A=40°,
∴∠ABC=(180°﹣∠A)=×(180°﹣40°)=70°,
∵MN垂直平分线AB,
∴AD=BD,
∴∠ABD=∠A=40°,
∴∠DBC=∠ABC﹣∠ABD=70°﹣40°=30°.
故答案为:30.
