人教版2021—2022学年八年级数学上册13.1轴对称 练习题 (word版、含答案)
文档属性
| 名称 | 人教版2021—2022学年八年级数学上册13.1轴对称 练习题 (word版、含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 405.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-01 15:10:46 | ||
图片预览




文档简介
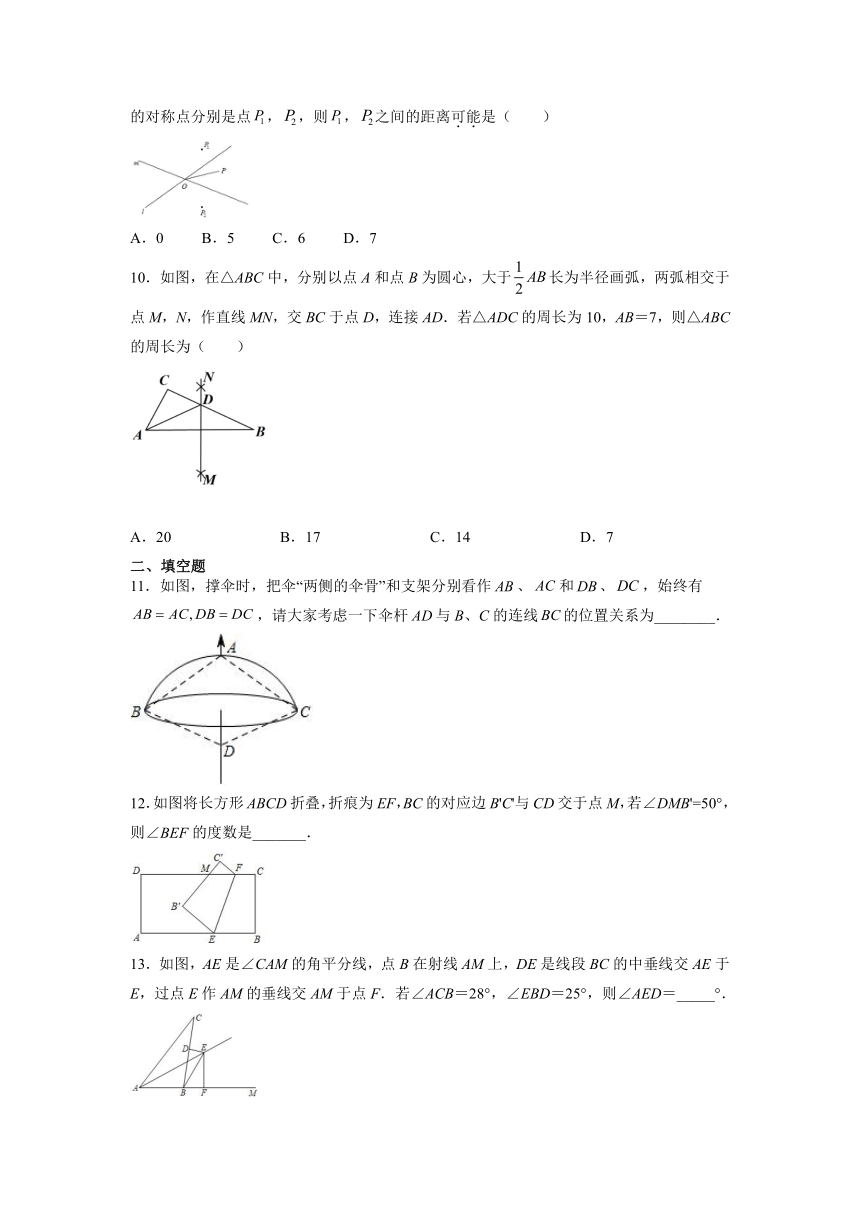
2021——2022学年度人教版八年级数学上册 第十三章轴对称 13.1轴对称 练习题
一、选择题
1.下列图形中,不是轴对称图形的是( )
A. B. C. D.
2.如图,已知长方形纸片ABCD,点E、H在AD边上,点F,G在BC边上,分别沿EF,GH折叠,使点B和点C都落在点P处,若,则∠IPK的度数为( )
A.129° B.128° C.127° D.126°
3.如图在四边形中,和都是直角,且.现将沿翻折,点的对应点为,与边相交于点,恰好是的角平分线,若,则的长为( )
A.1.5 B.1.6 C.2 D.3
4.正方形边长为a,点E、F分别是对角线上的两点,过点E、F分别作、的平行线,如图,则图中阴影部分的面积之和等于( )
A. B. C. D.2
5.如图,中,、分别是、上的点,作,,垂足分别是、,若,,下面四个结论:①;②;③≌;④垂直平分,其中正确结论的序号是( ).
A.①② B.①②③ C.①②④ D.①②③④
6.如图所示,在△ABC中,内角∠BAC与外角∠CBE的平分线相交于点P,,PGAD交BC于F,交AB于G,①;②S△PAC:S△PAB=PC:PB;③BP垂直平分CE;④∠PCF=∠CPF.其中正确的有( )
A.①②④ B.①③④ C.②③④ D.①③
7.如图,在锐角三角形中,,按以下步骤作图:①以点为圆心,长为半径作圆弧,交于点;②分别以点A、为圆心,大于长为半径作圆弧,计两弧交于点;③作射线,交于点,若,则的大小为( )
A. B. C. D.
8.如图,△ABC中,C、C′关于AB对称,B、B′关于AC对称,D、E分别在AB、AC上,且C′D∥BC∥B′E,BE,CD交于点F,若∠BFD=α,∠BAC=β,则α与β之间的关系为( )
A.2β+α=180° B.α=2β C.α= D.α=180°﹣
9.如图,直线,相交于点.为这两直线外一点,且.若点关于直线,的对称点分别是点,,则,之间的距离可能是( )
A.0 B.5 C.6 D.7
10.如图,在△ABC中,分别以点A和点B为圆心,大于长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为10,AB=7,则△ABC的周长为( )
A.20 B.17 C.14 D.7
二、填空题
11.如图,撑伞时,把伞“两侧的伞骨”和支架分别看作、和、,始终有,请大家考虑一下伞杆与B、C的连线的位置关系为________.
12.如图将长方形ABCD折叠,折痕为EF,BC的对应边B'C'与CD交于点M,若∠DMB'=50°,则∠BEF的度数是_______.
13.如图,AE是∠CAM的角平分线,点B在射线AM上,DE是线段BC的中垂线交AE于E,过点E作AM的垂线交AM于点F.若∠ACB=28°,∠EBD=25°,则∠AED=_____°.
14.如图,△ABC中,∠BAC=90°,AC=8cm,DE是BC边上的垂直平分线,△ABD的周长为14cm,则△ABC的面积是___cm2.
15.如图,在△ABC中,AC=6,按以下步骤作图:①分别以B,C为圆心,以大于BC的长为半径作弧,两弧相交于点M和N;②作直线MN交AC于D,连接BD.若BD=4,则AD=___.
三、解答题
16.如图所示,点A、B在直线l的同侧,,点C是点B关于直线l的对称点,交直线l于点D,,求的周长.
17.如图,直角坐标系中,点A在y轴上,轴于点C,点A关于直线的对称点D恰好在上,点E与点O关于直线对称,,求的度数.
18.如图,MN垂直平分线段AB,CD,垂足分别为点E,F,求证:,.
19.如图,AD与BC相交于点O,OA=OC,∠A=∠C,BE=DE.求证:BF=DF.
20.证明定理:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.已知:如图,A为线段外任意一点,且.求证:点A在的垂直平分线上.
21.如图,在△ABC中,AB≠AC,∠BAC的外角平分线交直线BC于D,过D作DE⊥AB,DF⊥AC分别交直线AB,AC于E,F,连接EF.
(1)求证:EF⊥AD;
(2)若DE∥AC,且DE=1,求AD的长.
22.画图探究:
(1)如图1,点和点位于直线两侧,是直线上一点,点使的值最小.请你通过画图,在图1中找出点;
(2)如图2,点和点位于直线同侧,是直线上一点,点使的值最小.请你通过画图,在图2中找出点;
实践应用:
(3)如图3,在四边形中,,,点在边上,点在边上,点、点使的周长的值最小.请你通过画图,在图3中找出点和点并求的度数.
23.如图中,,在射线上,在直线上.
(1)若是的2倍,求的度数;
(2)①用尺规作图,作射线(点在点的右边,不必写作法及证明);
②在①的基础上(即时),是的角平分线吗?为什么?
我知道,若让点在直线上移动,则的形状会随之改变.请你仔细观察,使用直尺和圆规,找出其它所有使也是等腰三角形的点的位置(按你找出的顺序将这些点记作、……).
【参考答案】
1.A 2.B 3.C 4.C 5.C 6.B 7.C 8.B 9.B 10.B
11.垂直
12.70°
13.37
14.24.
15.2
16.解:∵点C与点B关于直线l对称,
∴线段与线段关于直线l对称,
∴,
∴的周长.
17.解:连接OD, ∵BC⊥x轴于点C,∠OBC=25°,
∴∠AOB=∠OBC=25°,∠BOC=90°-25°=65°.
∵点A关于直线OB的对称点D恰好在BC上,
∴OB是线段AD的垂直平分线,
∴∠BOD=∠AOB=25°,
∴∠DOC=∠BOC-∠BOD=65°-25°=40°.
∵点E与点O关于直线BC对称,
∴BC是OE的垂直平分线,
∴∠DOC=∠OED=40°.
18.证明:如图,连接EC、ED,
∵MN垂直平分线段AB,∴,,又∵MN垂直平分线段CD,∴,由对称性得,,∴,即,在和中,
∴(SAS),
∴,,
又,∴,即.
19.证明:在△AOB与△COD中,
,
∴△AOB≌△COD(ASA),
∴OB=OD,
∴点O在线段BD的垂直平分线上,
∵BE=DE,
∴点E在线段BD的垂直平分线上,
∴OE垂直平分BD,
∴BF=DF.
20.证明:如图,作于点D,
∵,
∴,
在和中,
∴.
∴,
∴直线是线段的垂直平分线,
∴点A在的垂直平分线上.
21.(1)证明:∵AD是∠EAF的平分线,
∴∠EAD=∠DAF,
∵DE⊥AE,DF⊥AF,
∴∠DEA=∠DFA=90° ,
又AD=AD,
∴△DEA≌△DFA,
∴EA=FA,
∵ED=FD,
∴AD是EF的垂直平分线,
即AD⊥EF.
(2)解:∵DE∥AC,
∴∠DEA=∠FAE=90°,
又∠DFA=90°,
∴四边形EAFD是矩形,
由(1)得EA=FA,
∴四边形EAFD是正方形,
∵DE=1,
∴AD= .
22.解:(1)根据两点之间线段最短,连接与直线相交点,
此时最小;
(2)作点关于直线的对称点,则
,
连接与直线相交点即是点,此时最小,即最小;
(3)如图3,分别作出点关于,的对称点,,
连接分别交、于点、,此时周长最小;
∵,,
∴,∴,
∴.
∴.
23.(1)∵,
,
∵,
,
;
(2)①如图,
②是,理由如下:
如图所示,
∵,
∴,,
又∵,
∴,
∴是的角平分线.
(3)根据题意可知:点在直线上,是等腰三角形,可得三种情况满足:①B的左边和右边分别截取,可构成等腰三角形;②作AB的垂直平分线,交直线BN于C,连接即可;
一、选择题
1.下列图形中,不是轴对称图形的是( )
A. B. C. D.
2.如图,已知长方形纸片ABCD,点E、H在AD边上,点F,G在BC边上,分别沿EF,GH折叠,使点B和点C都落在点P处,若,则∠IPK的度数为( )
A.129° B.128° C.127° D.126°
3.如图在四边形中,和都是直角,且.现将沿翻折,点的对应点为,与边相交于点,恰好是的角平分线,若,则的长为( )
A.1.5 B.1.6 C.2 D.3
4.正方形边长为a,点E、F分别是对角线上的两点,过点E、F分别作、的平行线,如图,则图中阴影部分的面积之和等于( )
A. B. C. D.2
5.如图,中,、分别是、上的点,作,,垂足分别是、,若,,下面四个结论:①;②;③≌;④垂直平分,其中正确结论的序号是( ).
A.①② B.①②③ C.①②④ D.①②③④
6.如图所示,在△ABC中,内角∠BAC与外角∠CBE的平分线相交于点P,,PGAD交BC于F,交AB于G,①;②S△PAC:S△PAB=PC:PB;③BP垂直平分CE;④∠PCF=∠CPF.其中正确的有( )
A.①②④ B.①③④ C.②③④ D.①③
7.如图,在锐角三角形中,,按以下步骤作图:①以点为圆心,长为半径作圆弧,交于点;②分别以点A、为圆心,大于长为半径作圆弧,计两弧交于点;③作射线,交于点,若,则的大小为( )
A. B. C. D.
8.如图,△ABC中,C、C′关于AB对称,B、B′关于AC对称,D、E分别在AB、AC上,且C′D∥BC∥B′E,BE,CD交于点F,若∠BFD=α,∠BAC=β,则α与β之间的关系为( )
A.2β+α=180° B.α=2β C.α= D.α=180°﹣
9.如图,直线,相交于点.为这两直线外一点,且.若点关于直线,的对称点分别是点,,则,之间的距离可能是( )
A.0 B.5 C.6 D.7
10.如图,在△ABC中,分别以点A和点B为圆心,大于长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为10,AB=7,则△ABC的周长为( )
A.20 B.17 C.14 D.7
二、填空题
11.如图,撑伞时,把伞“两侧的伞骨”和支架分别看作、和、,始终有,请大家考虑一下伞杆与B、C的连线的位置关系为________.
12.如图将长方形ABCD折叠,折痕为EF,BC的对应边B'C'与CD交于点M,若∠DMB'=50°,则∠BEF的度数是_______.
13.如图,AE是∠CAM的角平分线,点B在射线AM上,DE是线段BC的中垂线交AE于E,过点E作AM的垂线交AM于点F.若∠ACB=28°,∠EBD=25°,则∠AED=_____°.
14.如图,△ABC中,∠BAC=90°,AC=8cm,DE是BC边上的垂直平分线,△ABD的周长为14cm,则△ABC的面积是___cm2.
15.如图,在△ABC中,AC=6,按以下步骤作图:①分别以B,C为圆心,以大于BC的长为半径作弧,两弧相交于点M和N;②作直线MN交AC于D,连接BD.若BD=4,则AD=___.
三、解答题
16.如图所示,点A、B在直线l的同侧,,点C是点B关于直线l的对称点,交直线l于点D,,求的周长.
17.如图,直角坐标系中,点A在y轴上,轴于点C,点A关于直线的对称点D恰好在上,点E与点O关于直线对称,,求的度数.
18.如图,MN垂直平分线段AB,CD,垂足分别为点E,F,求证:,.
19.如图,AD与BC相交于点O,OA=OC,∠A=∠C,BE=DE.求证:BF=DF.
20.证明定理:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.已知:如图,A为线段外任意一点,且.求证:点A在的垂直平分线上.
21.如图,在△ABC中,AB≠AC,∠BAC的外角平分线交直线BC于D,过D作DE⊥AB,DF⊥AC分别交直线AB,AC于E,F,连接EF.
(1)求证:EF⊥AD;
(2)若DE∥AC,且DE=1,求AD的长.
22.画图探究:
(1)如图1,点和点位于直线两侧,是直线上一点,点使的值最小.请你通过画图,在图1中找出点;
(2)如图2,点和点位于直线同侧,是直线上一点,点使的值最小.请你通过画图,在图2中找出点;
实践应用:
(3)如图3,在四边形中,,,点在边上,点在边上,点、点使的周长的值最小.请你通过画图,在图3中找出点和点并求的度数.
23.如图中,,在射线上,在直线上.
(1)若是的2倍,求的度数;
(2)①用尺规作图,作射线(点在点的右边,不必写作法及证明);
②在①的基础上(即时),是的角平分线吗?为什么?
我知道,若让点在直线上移动,则的形状会随之改变.请你仔细观察,使用直尺和圆规,找出其它所有使也是等腰三角形的点的位置(按你找出的顺序将这些点记作、……).
【参考答案】
1.A 2.B 3.C 4.C 5.C 6.B 7.C 8.B 9.B 10.B
11.垂直
12.70°
13.37
14.24.
15.2
16.解:∵点C与点B关于直线l对称,
∴线段与线段关于直线l对称,
∴,
∴的周长.
17.解:连接OD, ∵BC⊥x轴于点C,∠OBC=25°,
∴∠AOB=∠OBC=25°,∠BOC=90°-25°=65°.
∵点A关于直线OB的对称点D恰好在BC上,
∴OB是线段AD的垂直平分线,
∴∠BOD=∠AOB=25°,
∴∠DOC=∠BOC-∠BOD=65°-25°=40°.
∵点E与点O关于直线BC对称,
∴BC是OE的垂直平分线,
∴∠DOC=∠OED=40°.
18.证明:如图,连接EC、ED,
∵MN垂直平分线段AB,∴,,又∵MN垂直平分线段CD,∴,由对称性得,,∴,即,在和中,
∴(SAS),
∴,,
又,∴,即.
19.证明:在△AOB与△COD中,
,
∴△AOB≌△COD(ASA),
∴OB=OD,
∴点O在线段BD的垂直平分线上,
∵BE=DE,
∴点E在线段BD的垂直平分线上,
∴OE垂直平分BD,
∴BF=DF.
20.证明:如图,作于点D,
∵,
∴,
在和中,
∴.
∴,
∴直线是线段的垂直平分线,
∴点A在的垂直平分线上.
21.(1)证明:∵AD是∠EAF的平分线,
∴∠EAD=∠DAF,
∵DE⊥AE,DF⊥AF,
∴∠DEA=∠DFA=90° ,
又AD=AD,
∴△DEA≌△DFA,
∴EA=FA,
∵ED=FD,
∴AD是EF的垂直平分线,
即AD⊥EF.
(2)解:∵DE∥AC,
∴∠DEA=∠FAE=90°,
又∠DFA=90°,
∴四边形EAFD是矩形,
由(1)得EA=FA,
∴四边形EAFD是正方形,
∵DE=1,
∴AD= .
22.解:(1)根据两点之间线段最短,连接与直线相交点,
此时最小;
(2)作点关于直线的对称点,则
,
连接与直线相交点即是点,此时最小,即最小;
(3)如图3,分别作出点关于,的对称点,,
连接分别交、于点、,此时周长最小;
∵,,
∴,∴,
∴.
∴.
23.(1)∵,
,
∵,
,
;
(2)①如图,
②是,理由如下:
如图所示,
∵,
∴,,
又∵,
∴,
∴是的角平分线.
(3)根据题意可知:点在直线上,是等腰三角形,可得三种情况满足:①B的左边和右边分别截取,可构成等腰三角形;②作AB的垂直平分线,交直线BN于C,连接即可;
