2021-2022学年九年级数学上册 人教版 23.2.1中心对称同步练习(word版含解析)
文档属性
| 名称 | 2021-2022学年九年级数学上册 人教版 23.2.1中心对称同步练习(word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 509.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-01 15:31:08 | ||
图片预览



文档简介
2021-2022学年九年级数学上册(人教版)教材同步
23.2.1中心对称-同步练习
时间:60分钟
一、单选题
1.已知点P(-1-2a,2a-4)关于原点的对称点在第一象限,则整数a的值为( )
A.1 B.0
C.0,1 D.0,1,2
2.下列说法中,不正确的是( ).
A.关于某一点中心对称的两个图形全等
B.全等的图形一定关于某一点成中心对称
C.圆是中心对称图形
D.任何一条线段的两个端点关于这条线段的中点成中心对称
3.关于成中心对称的两个图形的性质,下列说法正确的是( )
A.连接对应点的线段都经过对称中心,并且被对称中心平分
B.成中心对称的两个图形的对应线段不一定相等
C.对应点的连线不一定都经过对称中心
D.以上说法都不对
4.下列几何图形中,①一条线段;②平面上的两条直线;③等边三角形;④平行四边形;⑤等腰三角形,其中一定是中心对称图形的有( )
A.2个 B.3个 C.4个 D.5个
5.如图,四边形ABCD与四边形FGHE关于一个点成中心对称,则这个点是( )
A.O1 B.O2 C.O3 D.O4
6.如图,线段AC与BD相交于点O,且△ABO和△CDO关于点O成中心对称,则下列结论,其中正确的个数是( )
①OB=OD;②AB=CD;③;④AC=BD.
A.4 B.3 C.2 D.1
7.如图,在平行四边形中,,为对角线,,边上的高为4,则图中阴影部分的面积为( )
A.3 B.6 C.12 D.24
8.如图,中,与关于点成中心对称,连接,当( )时,四边形为矩形.
A. B.
C. D.
二、填空题
9.如图,与关于O点成中心对称.则________,________,________.
10.如图,线段和关于点O中心对称,若,则的度数为________.
11.已知六边形ABCDEF是中心对称图形,AB=1,BC=2,CD=3,那么EF=_______.
12.如图,已知四边形ABCD及点O,要作一个四边形A′B′C′D′和四边形ABCD关于O点对称.
画法:(1)联结________并延长_______到点A′,使__________=_________,于是得到点A的对称点_____;
(2)同样画出B、C、D的对称点________、________、________;
(3)顺次联结_________、_________、________、_________,得四边形______就是所求四边形.
13.如图,若四边形ABCD与四边形CEFG成中心对称,则它们的对称中心是__,点A的对称点是__,点E的对称点是__.BD∥__且BD=__.连接点A,F的线段经过__,且被C点__,△ABD≌__.
14.在如图所示的平面直角坐标系中,是边长为2的等边三角形,作与关于点成中心对称,再作与关于点成中心对称,如此作下去,则的顶点的坐标是____.
三、解答题
15.如图(1)所示,魔术师把4张扑克牌放在桌子上,然后蒙住眼睛,请一位观众上台,把某一张牌旋转180°.魔术师解除蒙具后,看到4张扑克牌如图(2)所示,他很快确定了哪一张牌被旋转过.你能吗?
16.如图所示的两个图形成中心对称,请找出它的对称中点.
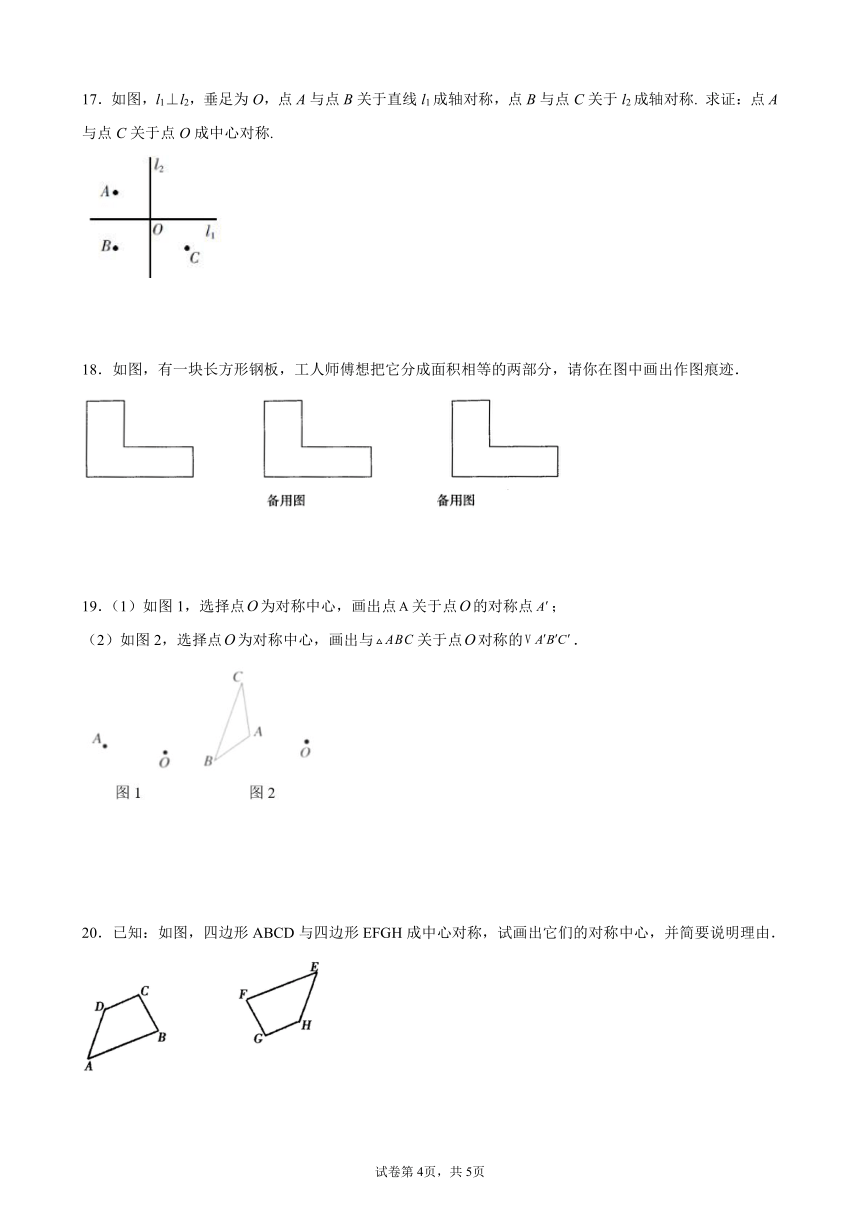
17.如图,l1⊥l2,垂足为O,点A与点B关于直线l1成轴对称,点B与点C关于l2成轴对称. 求证:点A与点C关于点O成中心对称.
18.如图,有一块长方形钢板,工人师傅想把它分成面积相等的两部分,请你在图中画出作图痕迹.
19.(1)如图1,选择点为对称中心,画出点关于点的对称点;
(2)如图2,选择点为对称中心,画出与关于点对称的.
20.已知:如图,四边形ABCD与四边形EFGH成中心对称,试画出它们的对称中心,并简要说明理由.
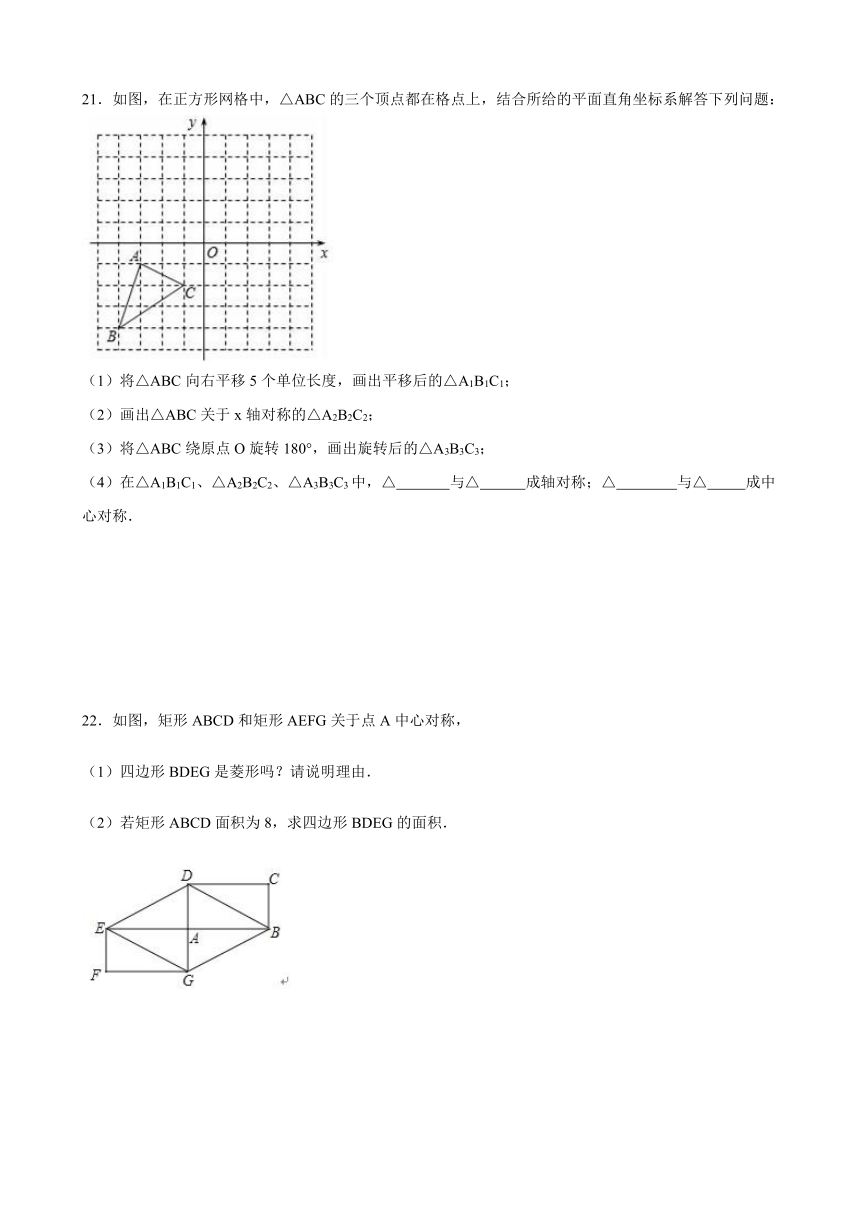
21.如图,在正方形网格中,△ABC的三个顶点都在格点上,结合所给的平面直角坐标系解答下列问题:
(1)将△ABC向右平移5个单位长度,画出平移后的△A1B1C1;
(2)画出△ABC关于x轴对称的△A2B2C2;
(3)将△ABC绕原点O旋转180°,画出旋转后的△A3B3C3;
(4)在△A1B1C1、△A2B2C2、△A3B3C3中,△ 与△ 成轴对称;△ 与△ 成中心对称.
22.如图,矩形ABCD和矩形AEFG关于点A中心对称,
(1)四边形BDEG是菱形吗?请说明理由.
(2)若矩形ABCD面积为8,求四边形BDEG的面积.
试卷第1页,共3页
参考答案
1.C
【解析】解:∵点P( 1 2a,2a 4)关于原点对称的点在第一象限,
∴点P在第三象限,
∴ ,
解得:∵a为整数,
∴a=0或1.
故选C.
2.B
【解析】A. 关于某一点中心对称的两个图形全等,正确;
B. 全等的图形不一定关于某一点成中心对称,故错误;
C. 圆是中心对称图形,正确;
D. 任何一条线段的两个端点关于这条线段的中点成中心对称,正确;
故选B.
3.A
【解析】根据中心对称的性质:
A. 连接对应点的线段都经过对称中心,并且被对称中心平分,此选项正确;
B. 根据成中心对称的两个图形的对应线段一定相等,故此选项错误;
C. 根据对应点的连线一定都经过对称中心,故此选项错误;
D. 以上说法都不对,此选项错误.
故答案选:A.
4.B
【解析】解:一条线段、平面上的两条直线以及平行四边形一定是中心对称图形,等边三角形、等腰三角形不是中心对称图形,符合题意的有3个,
故选择B.
5.A
【解析】如图,连接HC和DE交于O1,
故选A.
6.B
【解析】解:∵△ABO和△CDO关于点O成中心对称,
∴△ABO≌△CDO,
∴OB=OD,AB=CD,
而AC=BD不一定成立,
故选:B.
7.C
【解析】由题意,图中阴影部分的每一块关于平行四边形的中心对称图形都在平行四边形上,且都是非阴影的部分,所以由中心对称图形的性质可得:
所求的面积=.
故选C.
8.C
【解析】∵与关于点成中心对称
∴AC=CF,BC=EC
∴四边形AEFB是平行四边形
当AF=BE时,即BC=AC,四边形AEFB是矩形
又∵
∴△BCA为等边三角形,故
选C
9.=
【解析】∵与关于O点成中心对称,
∴,
∴,∠ABC=∠DEF
∴,
∴.
故答案为:=,EF,DF.
10.40°
【解析】解:∵线段和关于点O成中心对称,,
∵AO=CO,BO=DO,
又∵∠AOB=∠COD,
∴(SAS),
∴,
∴的度数为.
故答案为:40°.
11.2
【解析】解:∵六边形ABCDEF是中心对称图形,AB=1,BC=2,CD=3,
∴EF=BC=2.
故答案为:2
12.AO; AO; A’O; AO; A’; B’; C’; D’; C’ D’; D’ A’; A’ B’; B’C’; A’B’C’D’
【解析】解:①联结AO并延长AO到点A′,使AO=OA′,于是得到点A的对称点A′;
②同样画出B、C、D的对称点B′、C′、D′;
③顺次联结A′B′、B′C′、C′D′、D′A′得四边形A′B′C′D′就是所求四边形.
故答案为:AO、AO、AO、OA′、A';B′、C′、D′;A′B′、B′C′、C′D′、D′A′、A′B′C′D′.
13.点C 点F 点D EG EG 点C 平分 △FGE
【解析】四边形ABCD与四边形CEFG成中心对称,则它们的对称中心是C,点A的对称点是F,E的对称点是D.
BD∥EG且BD=EG.
连接A,F的线段经过C,且被C点平分,△ABD≌△FGE.
故答案为点C、点F、点D、EG、EG、点C、平分、△FGE.
14.
【解析】解:∵是边长为2的等边三角形,
∴的坐标为,的坐标为.
∵与关于点成中心对称,
∴点与点关于点成中心对称.
∴点的坐标是.
∵与关于点成中心对称,
∴点与点关于点成中心对称.
∴点的坐标是.
∵与关于点成中心对称,
∴点与点关于点成中心对称.
∴点的坐标是,…,
∴的横坐标是,的横坐标是,
∵当为奇数时,的纵坐标是,当为偶数时,的纵坐标是,
∴顶点的纵坐标是,
∴(是正整数)的顶点的坐标是,
∴的顶点的坐标.
故答案为:.
15.能,方法见解析
【解析】解:我能,方法如下:
图(1)与图(2)中扑克牌完全一样,说明被旋转过的牌是中心对称图形,
而图中只有方块4是中心对称图形,故方块4被旋转过.
16.见解析.
【解析】连接CC′,BB′,两条线段相交于当O,
则点O即为对称中点.
17.详见解析.
【解析】证明:以l1、l2所在直线分别为坐标轴建立平面直角坐标系,
设A点坐标为(a,b),
∵点A与点B关于直线l1(x轴)成轴对称,
∴B点坐标为(a,-b),
∵点B与点C关于l2(y轴)成轴对称,
∴C点坐标为(-a,-b),
∴点A与点C关于点O成中心对称.
18.答案见详解。
【解析】
解:解法一:钢板可看成由上下两个矩形构成(如图所示),矩形是中心对称图形,过对称中心的任一直线把矩形分成全等的两部分,自然平分其面积,而矩形的对称中心是两条对角线的交点,因此,先作出两矩形的对称中心,过两个对称中心做直线即可.
解法二:该钢板同样可看成左右两矩形构成(如图所示),作出两矩形对称中心,过两个对称中心做直线即可.
解法三:将钢板补成一个完整矩形(如图所示),作出大矩形对称中心和补上一块矩形的对称中心,过两个对称中心做直线即可
19.(1)见解析;(2)见解析
【解析】解:(1)如图,连接,在的延长线上截取,即可以求得点关于点的对称点.
(2)如图,作出,,三点关于点的对称点,,,依次连接,,,就可得到关于点对称的.
20.答案见详解。
【解析】
解:如图所示,点O即为对称中心.
理由如下:∵四边形ABCD与四边形EFGH成中心对称,
∴BF过对称中心,CG过对称中心,
∴BF、CG的交点即为对称中心.
21.△A2B2C2、△A3B3C3、△A1B1C1、△A3B3C3
【解析】(1)△A1B1C1如图所示:
(2)△A2B2C2如图所示:
(3)△A3B3C3如图所示:
(4)根据图形可得:△A2B2C2与△A3B3C3;△A1B1C1与△A3B3C3成轴对称图形.
22.(1)见解析; (2)16.
【解析】解:(1)四边形BDEG是菱形.
∵矩形ABCD和矩形AEFG关于点A中心对称,
∴AB=AE,AD=AG,BE⊥DG,
∴根据勾股定理得:BD2=DE2=EG2=GB2=AB2+AD2,
∴四边形BDEG是菱形.
(2)若矩形ABCD面积为8,则S△ABD=SABCD=4,
∴根据菱形性质:四边形BDEG的面积为SBDEG=4S△ABD=16.
答案第1页,共2页
答案第1页,共2页
23.2.1中心对称-同步练习
时间:60分钟
一、单选题
1.已知点P(-1-2a,2a-4)关于原点的对称点在第一象限,则整数a的值为( )
A.1 B.0
C.0,1 D.0,1,2
2.下列说法中,不正确的是( ).
A.关于某一点中心对称的两个图形全等
B.全等的图形一定关于某一点成中心对称
C.圆是中心对称图形
D.任何一条线段的两个端点关于这条线段的中点成中心对称
3.关于成中心对称的两个图形的性质,下列说法正确的是( )
A.连接对应点的线段都经过对称中心,并且被对称中心平分
B.成中心对称的两个图形的对应线段不一定相等
C.对应点的连线不一定都经过对称中心
D.以上说法都不对
4.下列几何图形中,①一条线段;②平面上的两条直线;③等边三角形;④平行四边形;⑤等腰三角形,其中一定是中心对称图形的有( )
A.2个 B.3个 C.4个 D.5个
5.如图,四边形ABCD与四边形FGHE关于一个点成中心对称,则这个点是( )
A.O1 B.O2 C.O3 D.O4
6.如图,线段AC与BD相交于点O,且△ABO和△CDO关于点O成中心对称,则下列结论,其中正确的个数是( )
①OB=OD;②AB=CD;③;④AC=BD.
A.4 B.3 C.2 D.1
7.如图,在平行四边形中,,为对角线,,边上的高为4,则图中阴影部分的面积为( )
A.3 B.6 C.12 D.24
8.如图,中,与关于点成中心对称,连接,当( )时,四边形为矩形.
A. B.
C. D.
二、填空题
9.如图,与关于O点成中心对称.则________,________,________.
10.如图,线段和关于点O中心对称,若,则的度数为________.
11.已知六边形ABCDEF是中心对称图形,AB=1,BC=2,CD=3,那么EF=_______.
12.如图,已知四边形ABCD及点O,要作一个四边形A′B′C′D′和四边形ABCD关于O点对称.
画法:(1)联结________并延长_______到点A′,使__________=_________,于是得到点A的对称点_____;
(2)同样画出B、C、D的对称点________、________、________;
(3)顺次联结_________、_________、________、_________,得四边形______就是所求四边形.
13.如图,若四边形ABCD与四边形CEFG成中心对称,则它们的对称中心是__,点A的对称点是__,点E的对称点是__.BD∥__且BD=__.连接点A,F的线段经过__,且被C点__,△ABD≌__.
14.在如图所示的平面直角坐标系中,是边长为2的等边三角形,作与关于点成中心对称,再作与关于点成中心对称,如此作下去,则的顶点的坐标是____.
三、解答题
15.如图(1)所示,魔术师把4张扑克牌放在桌子上,然后蒙住眼睛,请一位观众上台,把某一张牌旋转180°.魔术师解除蒙具后,看到4张扑克牌如图(2)所示,他很快确定了哪一张牌被旋转过.你能吗?
16.如图所示的两个图形成中心对称,请找出它的对称中点.
17.如图,l1⊥l2,垂足为O,点A与点B关于直线l1成轴对称,点B与点C关于l2成轴对称. 求证:点A与点C关于点O成中心对称.
18.如图,有一块长方形钢板,工人师傅想把它分成面积相等的两部分,请你在图中画出作图痕迹.
19.(1)如图1,选择点为对称中心,画出点关于点的对称点;
(2)如图2,选择点为对称中心,画出与关于点对称的.
20.已知:如图,四边形ABCD与四边形EFGH成中心对称,试画出它们的对称中心,并简要说明理由.
21.如图,在正方形网格中,△ABC的三个顶点都在格点上,结合所给的平面直角坐标系解答下列问题:
(1)将△ABC向右平移5个单位长度,画出平移后的△A1B1C1;
(2)画出△ABC关于x轴对称的△A2B2C2;
(3)将△ABC绕原点O旋转180°,画出旋转后的△A3B3C3;
(4)在△A1B1C1、△A2B2C2、△A3B3C3中,△ 与△ 成轴对称;△ 与△ 成中心对称.
22.如图,矩形ABCD和矩形AEFG关于点A中心对称,
(1)四边形BDEG是菱形吗?请说明理由.
(2)若矩形ABCD面积为8,求四边形BDEG的面积.
试卷第1页,共3页
参考答案
1.C
【解析】解:∵点P( 1 2a,2a 4)关于原点对称的点在第一象限,
∴点P在第三象限,
∴ ,
解得:
∴a=0或1.
故选C.
2.B
【解析】A. 关于某一点中心对称的两个图形全等,正确;
B. 全等的图形不一定关于某一点成中心对称,故错误;
C. 圆是中心对称图形,正确;
D. 任何一条线段的两个端点关于这条线段的中点成中心对称,正确;
故选B.
3.A
【解析】根据中心对称的性质:
A. 连接对应点的线段都经过对称中心,并且被对称中心平分,此选项正确;
B. 根据成中心对称的两个图形的对应线段一定相等,故此选项错误;
C. 根据对应点的连线一定都经过对称中心,故此选项错误;
D. 以上说法都不对,此选项错误.
故答案选:A.
4.B
【解析】解:一条线段、平面上的两条直线以及平行四边形一定是中心对称图形,等边三角形、等腰三角形不是中心对称图形,符合题意的有3个,
故选择B.
5.A
【解析】如图,连接HC和DE交于O1,
故选A.
6.B
【解析】解:∵△ABO和△CDO关于点O成中心对称,
∴△ABO≌△CDO,
∴OB=OD,AB=CD,
而AC=BD不一定成立,
故选:B.
7.C
【解析】由题意,图中阴影部分的每一块关于平行四边形的中心对称图形都在平行四边形上,且都是非阴影的部分,所以由中心对称图形的性质可得:
所求的面积=.
故选C.
8.C
【解析】∵与关于点成中心对称
∴AC=CF,BC=EC
∴四边形AEFB是平行四边形
当AF=BE时,即BC=AC,四边形AEFB是矩形
又∵
∴△BCA为等边三角形,故
选C
9.=
【解析】∵与关于O点成中心对称,
∴,
∴,∠ABC=∠DEF
∴,
∴.
故答案为:=,EF,DF.
10.40°
【解析】解:∵线段和关于点O成中心对称,,
∵AO=CO,BO=DO,
又∵∠AOB=∠COD,
∴(SAS),
∴,
∴的度数为.
故答案为:40°.
11.2
【解析】解:∵六边形ABCDEF是中心对称图形,AB=1,BC=2,CD=3,
∴EF=BC=2.
故答案为:2
12.AO; AO; A’O; AO; A’; B’; C’; D’; C’ D’; D’ A’; A’ B’; B’C’; A’B’C’D’
【解析】解:①联结AO并延长AO到点A′,使AO=OA′,于是得到点A的对称点A′;
②同样画出B、C、D的对称点B′、C′、D′;
③顺次联结A′B′、B′C′、C′D′、D′A′得四边形A′B′C′D′就是所求四边形.
故答案为:AO、AO、AO、OA′、A';B′、C′、D′;A′B′、B′C′、C′D′、D′A′、A′B′C′D′.
13.点C 点F 点D EG EG 点C 平分 △FGE
【解析】四边形ABCD与四边形CEFG成中心对称,则它们的对称中心是C,点A的对称点是F,E的对称点是D.
BD∥EG且BD=EG.
连接A,F的线段经过C,且被C点平分,△ABD≌△FGE.
故答案为点C、点F、点D、EG、EG、点C、平分、△FGE.
14.
【解析】解:∵是边长为2的等边三角形,
∴的坐标为,的坐标为.
∵与关于点成中心对称,
∴点与点关于点成中心对称.
∴点的坐标是.
∵与关于点成中心对称,
∴点与点关于点成中心对称.
∴点的坐标是.
∵与关于点成中心对称,
∴点与点关于点成中心对称.
∴点的坐标是,…,
∴的横坐标是,的横坐标是,
∵当为奇数时,的纵坐标是,当为偶数时,的纵坐标是,
∴顶点的纵坐标是,
∴(是正整数)的顶点的坐标是,
∴的顶点的坐标.
故答案为:.
15.能,方法见解析
【解析】解:我能,方法如下:
图(1)与图(2)中扑克牌完全一样,说明被旋转过的牌是中心对称图形,
而图中只有方块4是中心对称图形,故方块4被旋转过.
16.见解析.
【解析】连接CC′,BB′,两条线段相交于当O,
则点O即为对称中点.
17.详见解析.
【解析】证明:以l1、l2所在直线分别为坐标轴建立平面直角坐标系,
设A点坐标为(a,b),
∵点A与点B关于直线l1(x轴)成轴对称,
∴B点坐标为(a,-b),
∵点B与点C关于l2(y轴)成轴对称,
∴C点坐标为(-a,-b),
∴点A与点C关于点O成中心对称.
18.答案见详解。
【解析】
解:解法一:钢板可看成由上下两个矩形构成(如图所示),矩形是中心对称图形,过对称中心的任一直线把矩形分成全等的两部分,自然平分其面积,而矩形的对称中心是两条对角线的交点,因此,先作出两矩形的对称中心,过两个对称中心做直线即可.
解法二:该钢板同样可看成左右两矩形构成(如图所示),作出两矩形对称中心,过两个对称中心做直线即可.
解法三:将钢板补成一个完整矩形(如图所示),作出大矩形对称中心和补上一块矩形的对称中心,过两个对称中心做直线即可
19.(1)见解析;(2)见解析
【解析】解:(1)如图,连接,在的延长线上截取,即可以求得点关于点的对称点.
(2)如图,作出,,三点关于点的对称点,,,依次连接,,,就可得到关于点对称的.
20.答案见详解。
【解析】
解:如图所示,点O即为对称中心.
理由如下:∵四边形ABCD与四边形EFGH成中心对称,
∴BF过对称中心,CG过对称中心,
∴BF、CG的交点即为对称中心.
21.△A2B2C2、△A3B3C3、△A1B1C1、△A3B3C3
【解析】(1)△A1B1C1如图所示:
(2)△A2B2C2如图所示:
(3)△A3B3C3如图所示:
(4)根据图形可得:△A2B2C2与△A3B3C3;△A1B1C1与△A3B3C3成轴对称图形.
22.(1)见解析; (2)16.
【解析】解:(1)四边形BDEG是菱形.
∵矩形ABCD和矩形AEFG关于点A中心对称,
∴AB=AE,AD=AG,BE⊥DG,
∴根据勾股定理得:BD2=DE2=EG2=GB2=AB2+AD2,
∴四边形BDEG是菱形.
(2)若矩形ABCD面积为8,则S△ABD=SABCD=4,
∴根据菱形性质:四边形BDEG的面积为SBDEG=4S△ABD=16.
答案第1页,共2页
答案第1页,共2页
同课章节目录
