2021-2022学年人教版九年级数学上册24.1.2 垂直于弦的直径 同步练习 (word版含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学上册24.1.2 垂直于弦的直径 同步练习 (word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-01 15:49:07 | ||
图片预览

文档简介
24.1.2 垂直于弦的直径 课时训练
一、单项选择题(共8小题)
下列说法中,不正确的是
A. 圆既是轴对称图形,又是中心对称图形
B. 圆绕着它的圆心旋转任意角度,都能与自身重合
C. 圆的对称轴有无数条,对称中心只有一个
D. 圆的每一条直径都是它的对称轴
如图,DC是的直径,弦于点F,则下列结论不一定正确的是
A. B. C. D.
点P是内一点,过点P的最长弦的长为10cm,最短弦的长为6cm,则OP的长为
A. 3cm B. 4cm C. 5cm D. 6cm
往直径为52cm的圆柱形容器内装入一些水以后,截面如图所示,若水面宽,则水的最大深度为
A. 8cm B. 10cm C. 16cm D. 20cm
已知的半径为10cm,AB,CD是的两条弦,,,,则弦AB和CD之间的距离是
A. 2cm B. 14cm C. 2cm或14cm D. 以上都不对
如图所示,一条公路的转弯处是一段圆弧,点O是这段弧所在圆的圆心,,点C是的中点,点D是AB的中点,且,则这段弯路所在圆的半径为
A. B. C. D.
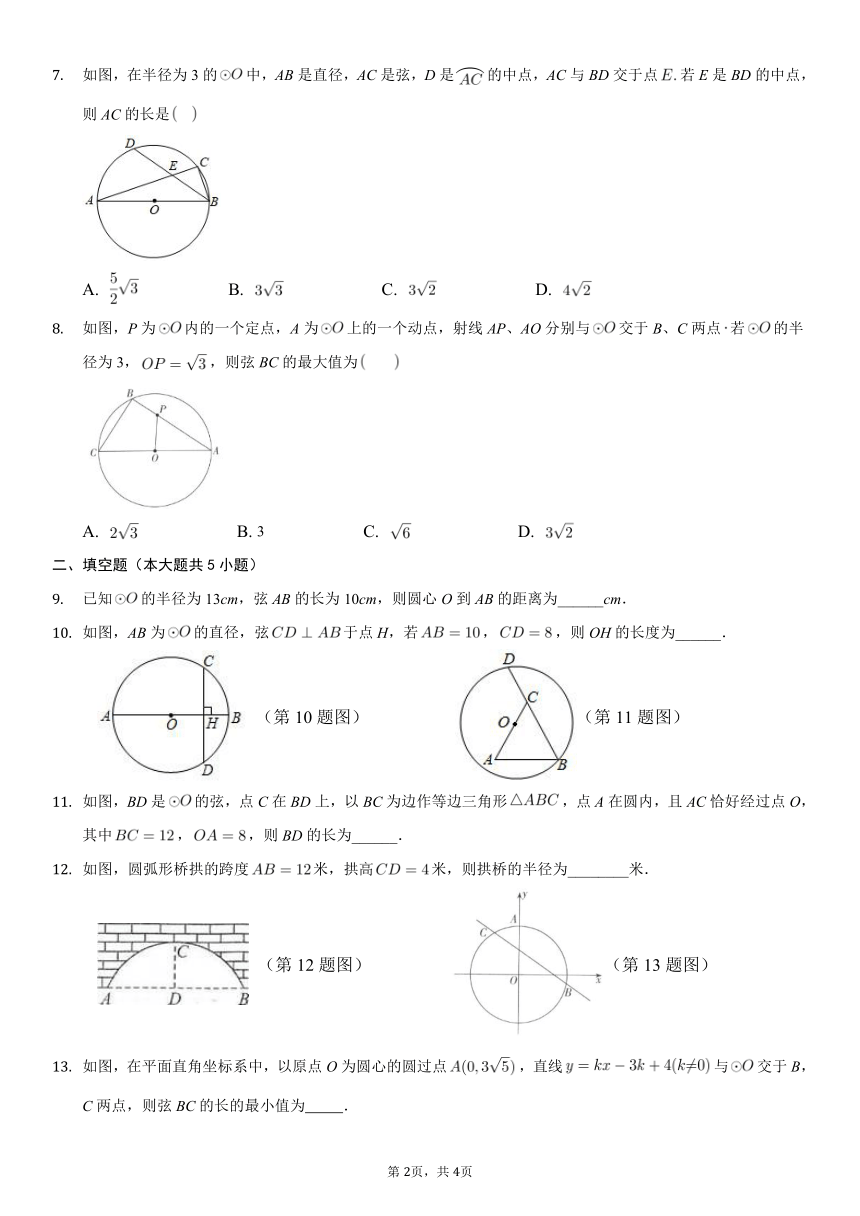
如图,在半径为3的中,AB是直径,AC是弦,D是的中点,AC与BD交于点若E是BD的中点,则AC的长是
A. B. C. D.
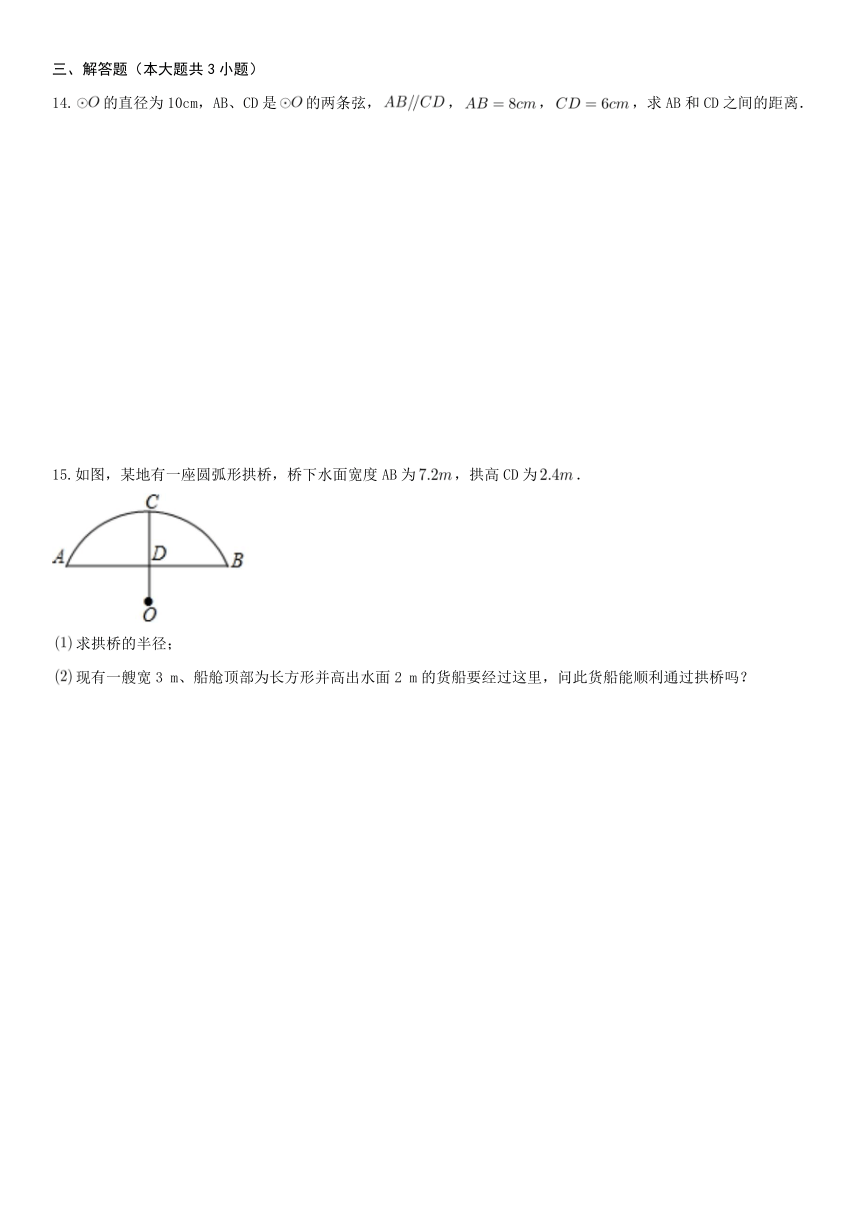
如图,P为内的一个定点,A为上的一个动点,射线AP、AO分别与交于B、C两点若的半径为3,,则弦BC的最大值为
A. B. 3 C. D.
二、填空题(本大题共5小题)
已知的半径为13cm,弦AB的长为10cm,则圆心O到AB的距离为______cm.
如图,AB为的直径,弦于点H,若,,则OH的长度为______.
(第10题图) (第11题图)
如图,BD是的弦,点C在BD上,以BC为边作等边三角形,点A在圆内,且AC恰好经过点O,其中,,则BD的长为______.
如图,圆弧形桥拱的跨度米,拱高米,则拱桥的半径为________米.
(第12题图) (第13题图)
如图,在平面直角坐标系中,以原点O为圆心的圆过点,直线与交于B,C两点,则弦BC的长的最小值为 .
三、解答题(本大题共3小题)
14.的直径为10cm,AB、CD是的两条弦,,,,求AB和CD之间的距离.
15.如图,某地有一座圆弧形拱桥,桥下水面宽度AB为,拱高CD为.
求拱桥的半径;
现有一艘宽3 m、船舱顶部为长方形并高出水面2 m的货船要经过这里,问此货船能顺利通过拱桥吗?
16.如图,D是的弦BC的中点,A是上一点,OA与BC交于点E,已知,.
求线段OD的长
当时,求ED的长.
第2页,共2页
答案和解析
1-8 DCBCC ADA
9、12
10、3
11、20
12、
13、
14、解:分两种情况考虑:
当两条弦位于圆心O一侧时,如图1所示,
过O作,交AB于点E,交CD于点F,连接OA,OC,
,,
、F分别为AB、CD的中点,
,,
在中,,,
根据勾股定理得:,
在中,,,
根据勾股定理得:,
则;
当两条弦位于圆心O两侧时,如图2所示,
同理可得,
综上,弦AB与CD的距离为7cm或1cm.
15、解:假设圆心在O处,连接OB,ON,过O作于D,交MN于E,交圆O于C点,如图:
设圆O的半径为r,则
,,,
又,所以,
在中,根据勾股定理得:
,
解得:,
即:拱桥的半径是米,
,
当时,,则
,
解得,
米米.
此货船能顺利通过这座拱形桥.
16、解:如图,连接OB.
过圆心,且D是弦BC的中点,
,.
在中,由勾股定理得,
.
.
设,则,.
在中,由勾股定理得,
.
解得舍去,.
.
一、单项选择题(共8小题)
下列说法中,不正确的是
A. 圆既是轴对称图形,又是中心对称图形
B. 圆绕着它的圆心旋转任意角度,都能与自身重合
C. 圆的对称轴有无数条,对称中心只有一个
D. 圆的每一条直径都是它的对称轴
如图,DC是的直径,弦于点F,则下列结论不一定正确的是
A. B. C. D.
点P是内一点,过点P的最长弦的长为10cm,最短弦的长为6cm,则OP的长为
A. 3cm B. 4cm C. 5cm D. 6cm
往直径为52cm的圆柱形容器内装入一些水以后,截面如图所示,若水面宽,则水的最大深度为
A. 8cm B. 10cm C. 16cm D. 20cm
已知的半径为10cm,AB,CD是的两条弦,,,,则弦AB和CD之间的距离是
A. 2cm B. 14cm C. 2cm或14cm D. 以上都不对
如图所示,一条公路的转弯处是一段圆弧,点O是这段弧所在圆的圆心,,点C是的中点,点D是AB的中点,且,则这段弯路所在圆的半径为
A. B. C. D.
如图,在半径为3的中,AB是直径,AC是弦,D是的中点,AC与BD交于点若E是BD的中点,则AC的长是
A. B. C. D.
如图,P为内的一个定点,A为上的一个动点,射线AP、AO分别与交于B、C两点若的半径为3,,则弦BC的最大值为
A. B. 3 C. D.
二、填空题(本大题共5小题)
已知的半径为13cm,弦AB的长为10cm,则圆心O到AB的距离为______cm.
如图,AB为的直径,弦于点H,若,,则OH的长度为______.
(第10题图) (第11题图)
如图,BD是的弦,点C在BD上,以BC为边作等边三角形,点A在圆内,且AC恰好经过点O,其中,,则BD的长为______.
如图,圆弧形桥拱的跨度米,拱高米,则拱桥的半径为________米.
(第12题图) (第13题图)
如图,在平面直角坐标系中,以原点O为圆心的圆过点,直线与交于B,C两点,则弦BC的长的最小值为 .
三、解答题(本大题共3小题)
14.的直径为10cm,AB、CD是的两条弦,,,,求AB和CD之间的距离.
15.如图,某地有一座圆弧形拱桥,桥下水面宽度AB为,拱高CD为.
求拱桥的半径;
现有一艘宽3 m、船舱顶部为长方形并高出水面2 m的货船要经过这里,问此货船能顺利通过拱桥吗?
16.如图,D是的弦BC的中点,A是上一点,OA与BC交于点E,已知,.
求线段OD的长
当时,求ED的长.
第2页,共2页
答案和解析
1-8 DCBCC ADA
9、12
10、3
11、20
12、
13、
14、解:分两种情况考虑:
当两条弦位于圆心O一侧时,如图1所示,
过O作,交AB于点E,交CD于点F,连接OA,OC,
,,
、F分别为AB、CD的中点,
,,
在中,,,
根据勾股定理得:,
在中,,,
根据勾股定理得:,
则;
当两条弦位于圆心O两侧时,如图2所示,
同理可得,
综上,弦AB与CD的距离为7cm或1cm.
15、解:假设圆心在O处,连接OB,ON,过O作于D,交MN于E,交圆O于C点,如图:
设圆O的半径为r,则
,,,
又,所以,
在中,根据勾股定理得:
,
解得:,
即:拱桥的半径是米,
,
当时,,则
,
解得,
米米.
此货船能顺利通过这座拱形桥.
16、解:如图,连接OB.
过圆心,且D是弦BC的中点,
,.
在中,由勾股定理得,
.
.
设,则,.
在中,由勾股定理得,
.
解得舍去,.
.
同课章节目录
