二冰淇淋盒有多大 圆柱和圆锥 信息窗2 圆柱的侧面积和表面积 课件(共22张PPT)
文档属性
| 名称 | 二冰淇淋盒有多大 圆柱和圆锥 信息窗2 圆柱的侧面积和表面积 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-01 10:15:39 | ||
图片预览





文档简介
(共22张PPT)
圆柱的侧面积和表面积
青岛版数学六年级(下)
二 冰淇淋盒有多大
——圆柱和圆锥
认识圆柱的展开图,理解圆柱侧面积和表面积的含义。
探索和掌握圆柱侧面积和表面积的计算方法,并能解决生活中相应的实际问题。
学习目标
探索和掌握圆柱侧面积和表面积的计算方法,并能解决生活中相应的实际问题。
掌握圆柱侧面积和表面积的计算方法。
【难点】
【重点】
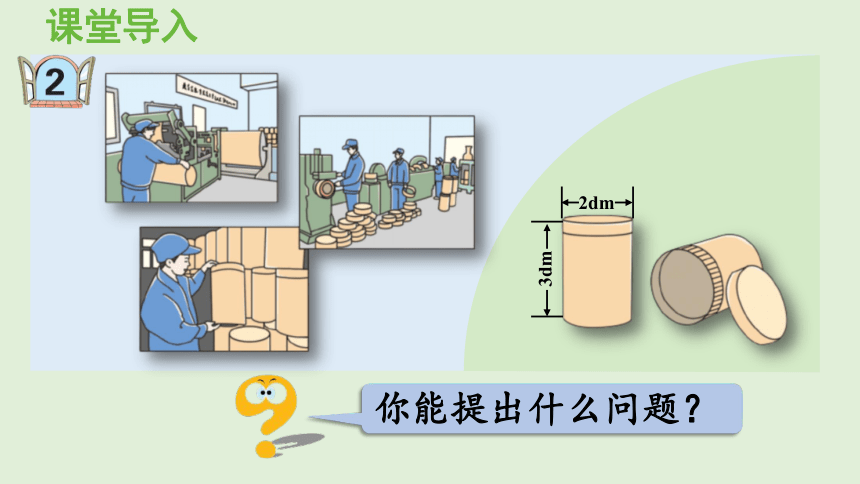
课堂导入
你能提出什么问题?
2dm
3dm
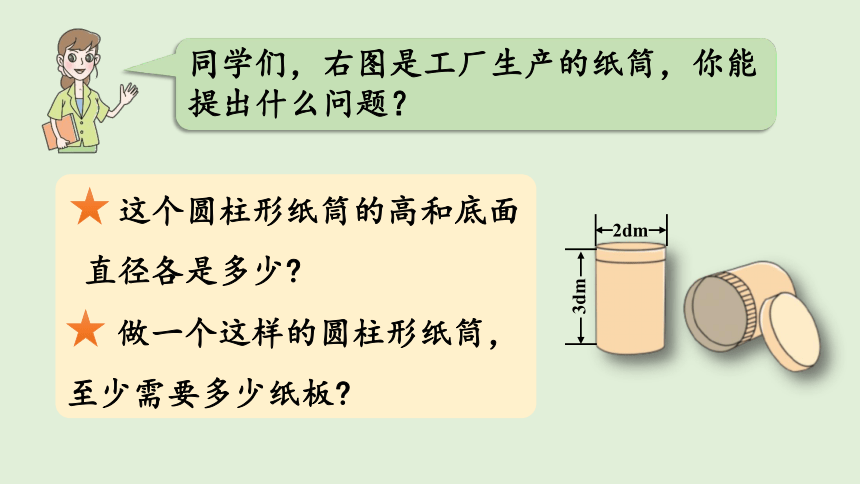
同学们,右图是工厂生产的纸筒,你能提出什么问题?
2dm
3dm
这个圆柱形纸筒的高和底面直径各是多少
做一个这样的圆柱形纸筒,至少需要多少纸板
做一个这样的圆柱形纸筒,至少需要多少纸板?
新知探究
求需要多少纸板,也就是求圆柱形纸筒的表面积。
底面
高
我发现,圆柱的侧面积加上两个底面的面积就是圆柱的表面积。
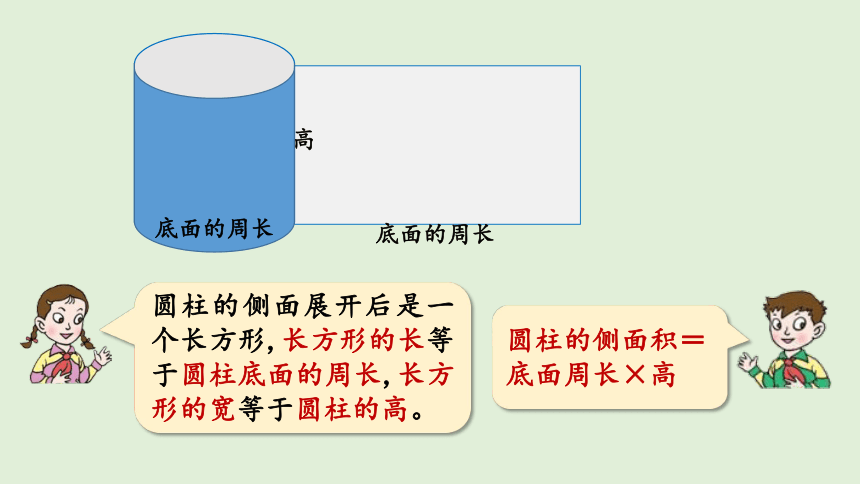
我沿着高将 剪开。
底面的周长
高
底面
底面
底面的周长
高
底面
底面
底面的周长
底面的周长
高
圆柱的侧面展开后是一个长方形,长方形的长等于圆柱底面的周长,长方形的宽等于圆柱的高。
圆柱的侧面积=底面周长×高
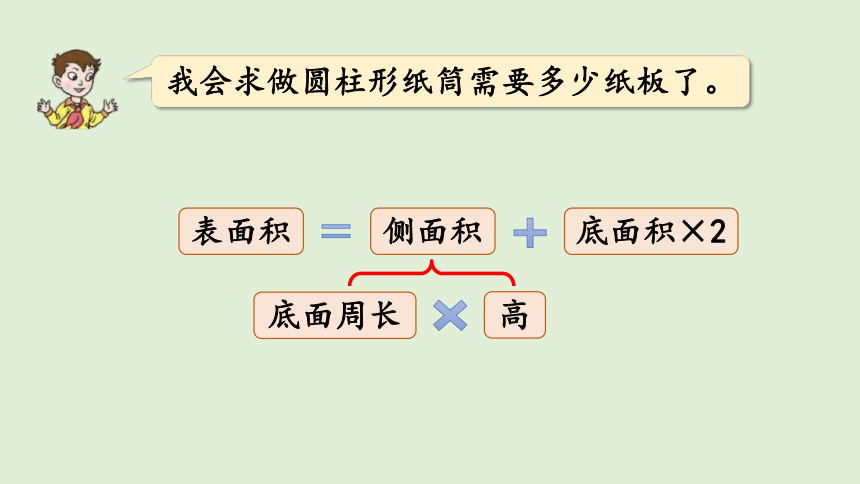
我会求做圆柱形纸筒需要多少纸板了。
表面积
侧面积
底面积×2
底面周长
高
我会求做圆柱形纸筒需要多少纸板了。
答:做一个这样的圆柱形纸筒,至少需要25.12平方分米纸板。
侧面积:3.14×2×3=18.84(平方分米)
底面积:3.14×(2÷2)2=3.14(平方分米)
表面积:18.84+3.14×2=25.12(平方分米)
10
5
侧面积:
底面积:
表面积:
3.14×5×2×10
=314(dm2)
3.14×52
=78.5(dm2)
314+78.5×2
=471(dm2)
课堂练习
1
计算下列圆柱的侧面积和表面积。
(单位:dm)
(教材第21页“自主练习”第1题)
4.5
2
侧面积:
底面积:
表面积:
3.14×2×4.5
=28.26(dm2)
3.14×(2÷2)2
=3.14(dm2)
28.26+3.14×2
=34.54(dm2)
一台压路机的前轮是圆柱形,轮宽2米,直径为1.2米。
2
分析:
(1)
压路机的前轮是圆柱形,滚动一周,压过的路面面积就是前轮的侧面积。
3.14×1.2×2
=7.536(平方米)
答:前轮滚动一周,压过的路面是7.536平方米。
(2)如果每分钟滚动15周,压过的 路面是多少平方米
(1)前轮滚动一周,压过的路面是 多少平方米
分析:
(2)
上一问中,我们已经计算出滚动一周压过的路面面积是7.536平方米。计算每分钟压过的路面面积,就是用压路机前轮侧面积×每分钟滚动的周数。
7.536×15
=113.04(平方米)
答:每分钟滚动15周,压过的路面是113.04平方米。
(教材第21页“自主练习”第3题)
一个鱼缸的侧面是用钢化玻璃制成的。制作这样一个鱼缸,至少需要多少平方米的钢化玻璃
3
分析:
根据题意知,鱼缸的侧面用钢化玻璃制成,要计算出制作鱼缸需要的钢化玻璃面积,就是要计算鱼缸的侧面积。
3.14×2×3
=18.84(m2)
答:至少需要18.84 m2钢化玻璃。
(教材第22页“自主练习”第4题)
王师傅准备了下列不同规格的材料,怎样选才能做成圆柱形的盒子
4
①
②
9.42cm
6.28cm
12.56cm
9.42cm
2cm
2cm
3cm
3cm
4cm
4cm
(教材第22页“自主练习”第5题)
分析
通过学习,我们已经知道:
圆柱侧面展开图是一个长方形,这个长方形的一条边等于底面周长,另一条边等于圆柱的高。
要做成圆柱形的盒子,则要确保圆形材料的周长与长方形的任一个边长相等。
直径为2cm的圆形材料周长为3.14×2=6.28()
直径为3cm的圆形材料周长为3.14×3=9.42()
直径为4cm的圆形材料周长为3.14×4=12.56()
用直径为2cm的圆形材料和②号长方形材料可制作一个圆柱形的盒子,其高为12.56。
用直径为3cm的圆形材料和①号长方形材料可制作一个圆柱形的盒子,其高为9.42。
用直径为4cm的圆形材料和②号长方形材料可制作一个圆柱形的盒子,其高为6.28。
填表。
5
底面半径 底面周长 高 圆柱的侧面积 圆柱的表面积
2cm 3cm
18.84cm 6cm
12.56cm
37.68cm2
62.8cm2
3cm
113.04cm2
169.56cm2
(教材第22页“自主练习”第6题)
孔府门前有4根柱子,每根高3.7米,横截面周长为1.25米。如果每平方米用油漆0.2千克,漆这4根柱子要用多少千克油漆
6
分析:
柱子是圆柱形的,漆柱子只用漆其侧面。
一根柱子的侧面积:
共需涂漆面积:
所需油漆:
3.7×1.25
=4.625(平方米)
4.625×4
=18.5(平方米)
18.5×0.2
=3.7(千克)
答:漆这4根柱子要用3.7千克油漆。
(教材第23页“自主练习”第8题)
下图是一个圆柱的展开图。这个圆柱的表面积是多少
7
62.8cm
40cm
侧面积:
底面积:
表面积:
62.8×40
=2512(cm2)
3.14×102
=314(cm2)
2512+314×2
=3140(cm2)
底面半径:
62.8÷3.14÷2
=10(cm)
底面周长为62.8cm;
圆柱的高为40cm。
已知:
答:这个圆柱的表面积是3140cm2。
(教材第23页“自主练习”第11题)
一根圆柱形木料,底面积是6平方分米,把它截成4段,表面积增加了多少平方分米
分析:
8
一根圆柱形木料被锯成4段,这段木料的侧面积未变,但是增加了6个底面面积,所以表面积增加了6个底面的面积和。
增加的面
已知底面积为6平方分米,所以增加的表面积为:
6×[2×(4-1)]
=36(平方分米)
答:增加的表面积为36平方分米。
(教材第23页“自主练习”第13题)
课堂小结
圆柱的表面积是由哪些部分的面积构成的,要怎么计算呢?
圆柱的表面积由侧面的面积和两个底面的面积组成。计算圆柱的表面积就将侧面积和底面积加起来。
圆柱的侧面展开图是一个长方形,计算侧面积就是用圆柱的底面周长乘以圆柱的高。
课后作业
作业课件中的相关练习。
02
01
课后练习第2、7、9、10、12题。
圆柱的侧面积和表面积
青岛版数学六年级(下)
二 冰淇淋盒有多大
——圆柱和圆锥
认识圆柱的展开图,理解圆柱侧面积和表面积的含义。
探索和掌握圆柱侧面积和表面积的计算方法,并能解决生活中相应的实际问题。
学习目标
探索和掌握圆柱侧面积和表面积的计算方法,并能解决生活中相应的实际问题。
掌握圆柱侧面积和表面积的计算方法。
【难点】
【重点】
课堂导入
你能提出什么问题?
2dm
3dm
同学们,右图是工厂生产的纸筒,你能提出什么问题?
2dm
3dm
这个圆柱形纸筒的高和底面直径各是多少
做一个这样的圆柱形纸筒,至少需要多少纸板
做一个这样的圆柱形纸筒,至少需要多少纸板?
新知探究
求需要多少纸板,也就是求圆柱形纸筒的表面积。
底面
高
我发现,圆柱的侧面积加上两个底面的面积就是圆柱的表面积。
我沿着高将 剪开。
底面的周长
高
底面
底面
底面的周长
高
底面
底面
底面的周长
底面的周长
高
圆柱的侧面展开后是一个长方形,长方形的长等于圆柱底面的周长,长方形的宽等于圆柱的高。
圆柱的侧面积=底面周长×高
我会求做圆柱形纸筒需要多少纸板了。
表面积
侧面积
底面积×2
底面周长
高
我会求做圆柱形纸筒需要多少纸板了。
答:做一个这样的圆柱形纸筒,至少需要25.12平方分米纸板。
侧面积:3.14×2×3=18.84(平方分米)
底面积:3.14×(2÷2)2=3.14(平方分米)
表面积:18.84+3.14×2=25.12(平方分米)
10
5
侧面积:
底面积:
表面积:
3.14×5×2×10
=314(dm2)
3.14×52
=78.5(dm2)
314+78.5×2
=471(dm2)
课堂练习
1
计算下列圆柱的侧面积和表面积。
(单位:dm)
(教材第21页“自主练习”第1题)
4.5
2
侧面积:
底面积:
表面积:
3.14×2×4.5
=28.26(dm2)
3.14×(2÷2)2
=3.14(dm2)
28.26+3.14×2
=34.54(dm2)
一台压路机的前轮是圆柱形,轮宽2米,直径为1.2米。
2
分析:
(1)
压路机的前轮是圆柱形,滚动一周,压过的路面面积就是前轮的侧面积。
3.14×1.2×2
=7.536(平方米)
答:前轮滚动一周,压过的路面是7.536平方米。
(2)如果每分钟滚动15周,压过的 路面是多少平方米
(1)前轮滚动一周,压过的路面是 多少平方米
分析:
(2)
上一问中,我们已经计算出滚动一周压过的路面面积是7.536平方米。计算每分钟压过的路面面积,就是用压路机前轮侧面积×每分钟滚动的周数。
7.536×15
=113.04(平方米)
答:每分钟滚动15周,压过的路面是113.04平方米。
(教材第21页“自主练习”第3题)
一个鱼缸的侧面是用钢化玻璃制成的。制作这样一个鱼缸,至少需要多少平方米的钢化玻璃
3
分析:
根据题意知,鱼缸的侧面用钢化玻璃制成,要计算出制作鱼缸需要的钢化玻璃面积,就是要计算鱼缸的侧面积。
3.14×2×3
=18.84(m2)
答:至少需要18.84 m2钢化玻璃。
(教材第22页“自主练习”第4题)
王师傅准备了下列不同规格的材料,怎样选才能做成圆柱形的盒子
4
①
②
9.42cm
6.28cm
12.56cm
9.42cm
2cm
2cm
3cm
3cm
4cm
4cm
(教材第22页“自主练习”第5题)
分析
通过学习,我们已经知道:
圆柱侧面展开图是一个长方形,这个长方形的一条边等于底面周长,另一条边等于圆柱的高。
要做成圆柱形的盒子,则要确保圆形材料的周长与长方形的任一个边长相等。
直径为2cm的圆形材料周长为3.14×2=6.28()
直径为3cm的圆形材料周长为3.14×3=9.42()
直径为4cm的圆形材料周长为3.14×4=12.56()
用直径为2cm的圆形材料和②号长方形材料可制作一个圆柱形的盒子,其高为12.56。
用直径为3cm的圆形材料和①号长方形材料可制作一个圆柱形的盒子,其高为9.42。
用直径为4cm的圆形材料和②号长方形材料可制作一个圆柱形的盒子,其高为6.28。
填表。
5
底面半径 底面周长 高 圆柱的侧面积 圆柱的表面积
2cm 3cm
18.84cm 6cm
12.56cm
37.68cm2
62.8cm2
3cm
113.04cm2
169.56cm2
(教材第22页“自主练习”第6题)
孔府门前有4根柱子,每根高3.7米,横截面周长为1.25米。如果每平方米用油漆0.2千克,漆这4根柱子要用多少千克油漆
6
分析:
柱子是圆柱形的,漆柱子只用漆其侧面。
一根柱子的侧面积:
共需涂漆面积:
所需油漆:
3.7×1.25
=4.625(平方米)
4.625×4
=18.5(平方米)
18.5×0.2
=3.7(千克)
答:漆这4根柱子要用3.7千克油漆。
(教材第23页“自主练习”第8题)
下图是一个圆柱的展开图。这个圆柱的表面积是多少
7
62.8cm
40cm
侧面积:
底面积:
表面积:
62.8×40
=2512(cm2)
3.14×102
=314(cm2)
2512+314×2
=3140(cm2)
底面半径:
62.8÷3.14÷2
=10(cm)
底面周长为62.8cm;
圆柱的高为40cm。
已知:
答:这个圆柱的表面积是3140cm2。
(教材第23页“自主练习”第11题)
一根圆柱形木料,底面积是6平方分米,把它截成4段,表面积增加了多少平方分米
分析:
8
一根圆柱形木料被锯成4段,这段木料的侧面积未变,但是增加了6个底面面积,所以表面积增加了6个底面的面积和。
增加的面
已知底面积为6平方分米,所以增加的表面积为:
6×[2×(4-1)]
=36(平方分米)
答:增加的表面积为36平方分米。
(教材第23页“自主练习”第13题)
课堂小结
圆柱的表面积是由哪些部分的面积构成的,要怎么计算呢?
圆柱的表面积由侧面的面积和两个底面的面积组成。计算圆柱的表面积就将侧面积和底面积加起来。
圆柱的侧面展开图是一个长方形,计算侧面积就是用圆柱的底面周长乘以圆柱的高。
课后作业
作业课件中的相关练习。
02
01
课后练习第2、7、9、10、12题。
