2018-2019学年黑龙江省鸡西市密山实验中学八年级(上)期中数学试卷(五四学制)(Word版 含解析)
文档属性
| 名称 | 2018-2019学年黑龙江省鸡西市密山实验中学八年级(上)期中数学试卷(五四学制)(Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 401.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-01 00:00:00 | ||
图片预览




文档简介
2018-2019学年黑龙江省鸡西市密山实验中学八年级(上)期中数学试卷(五四学制)
一、填空题(每小题3分,共30分)
1.(3分)若点P在线段AB的垂直平分线上,PA=5,则PB= .
2.(3分)若分式有意义,则x的取值范围为 .
3.(3分)已知点A(x,﹣4)与点B(3,y)关于x轴对称 .
4.(3分)如图,在△ABC中,DE是AC的垂直平分线,△ABD的周长为13cm,则△ABC的周长是 cm.
5.(3分)如图,在Rt△ABC中,∠C=90°,BD是∠ABC的平分线,若BD=10 .
6.(3分)如图,在△ABC中,AB=AC,若∠A=40°,则∠ABD= .
7.(3分)当a 时,(a﹣)0=1.
8.(3分)若5x﹣3y﹣2=0,则105x÷103y= .
9.(3分)在平面直角坐标系中,已知A坐标(﹣2,2),在y轴上确定一点P,则符合条件的点P共有 个.
10.(3分)观察下列图形它们是按一定规律排列的,依照此规律,第20个图形共有 个★.
二、选择题(每小题3分,共30分)
11.(3分)下列计算中正确的是( )
A.a2+b3=2a5 B.a4÷a=a4 C.a2 a4=a8 D.(﹣a2)3=﹣a6
12.(3分)下面有4个汽车标志图案,其中是轴对称图形的是( )
A.②③④ B.①③④ C.①②④ D.①②③
13.(3分)如图,已知△ABC是等边三角形,点O是BC上任意一点,OF分别于两边垂直,等边三角形的高为2( )
A.1 B.3 C.2 D.4
14.(3分)如图,AC=BC=10cm,∠B=15°,则AD的长为( )
A.3cm B.4cm C.5cm D.6cm
15.(3分)若x2+kxy+9y2是一个完全平方式,则k的取值为( )
A.±6 B.6 C.3 D.±81
16.(3分)已知a2+b2=25,且ab=12,则(a+b)2的值是( )
A.13 B.49 C.37 D.1
17.(3分)下列约分正确的是( )
A. B.
C. D.
18.(3分)已知等腰三角形一腰上的高与另一腰的夹角为60°,则这个等腰三角形的顶角是( )
A.30° B.60° C.150° D.30°或150°
19.(3分)如(x+m)与(x+3)的乘积中不含x的一次项,则m的值为( )
A.﹣3 B.3 C.0 D.1
20.(3分)如图所示,已知△ABC和△CDE均是等边三角形,点B、C、D在同一条直线上,AD与CE交于点N,AC与BE交于点M,则下列结论:①AD=BE;②AN=BM;④∠BOC=∠DOC,⑤△CMN为等边三角形,则∠BED=100°.其中正确的结论个数为( )
A.3个 B.4个 C.5个 D.6个
三、解答题(共60分)
21.(10分)先化简再求值
(1)x2(x﹣1)﹣x(x2+x﹣1),其中;
(2)(2x+3y)2﹣(2x+y)(2x﹣y)其中.
22.(8分)计算
(1)(x﹣2)(x2+4);
(2)(6x4÷8x3)÷(﹣2x2);
(3)(2a﹣3b)(3b+2a);
(4)(2a+b+c)2.
23.(8分)因式分解
(1)x3﹣9x;
(2)25x2﹣16y2;
(3)(m+n)2﹣4m(m+n)+4m2;
(4)(a﹣b)2+4ab.
24.(4分)已知(x+y)2=25,(x﹣y)2=9,求xy与x2+y2的值.
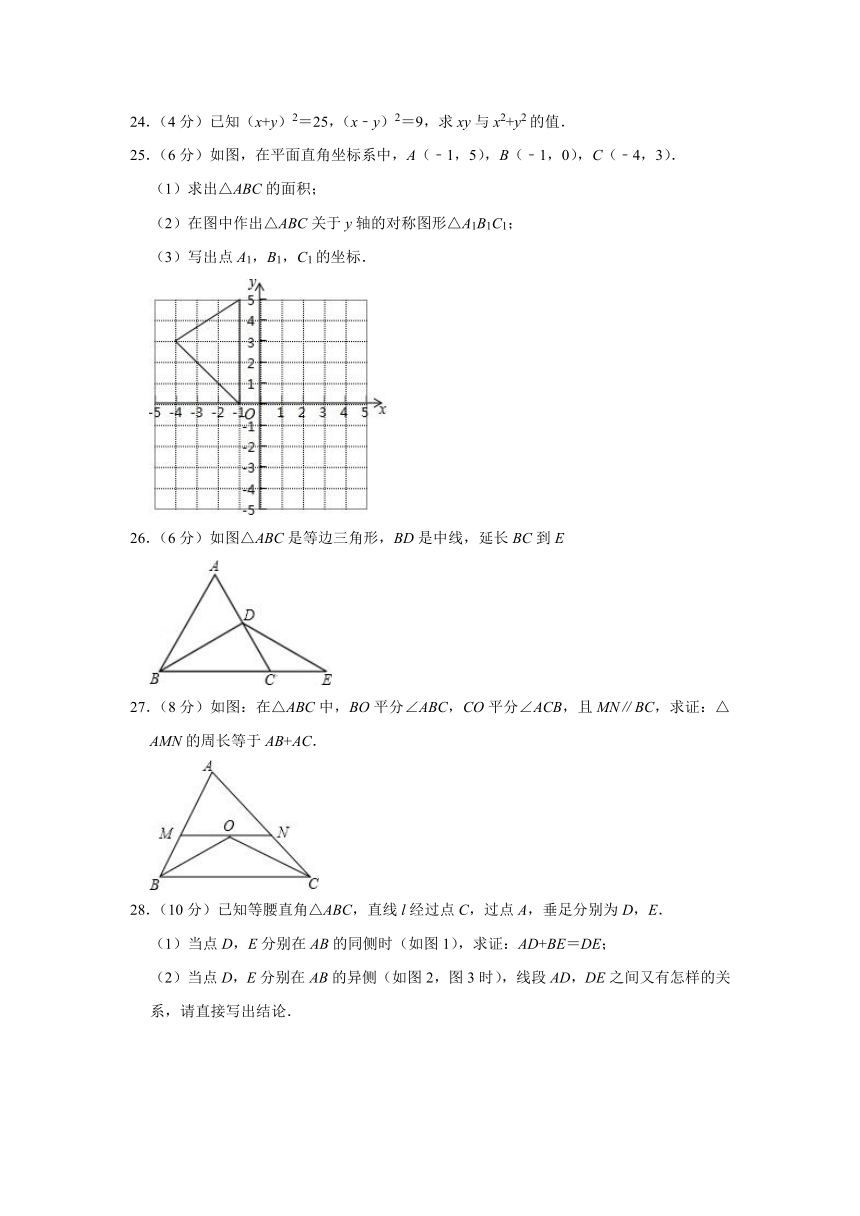
25.(6分)如图,在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
(1)求出△ABC的面积;
(2)在图中作出△ABC关于y轴的对称图形△A1B1C1;
(3)写出点A1,B1,C1的坐标.
26.(6分)如图△ABC是等边三角形,BD是中线,延长BC到E
27.(8分)如图:在△ABC中,BO平分∠ABC,CO平分∠ACB,且MN∥BC,求证:△AMN的周长等于AB+AC.
28.(10分)已知等腰直角△ABC,直线l经过点C,过点A,垂足分别为D,E.
(1)当点D,E分别在AB的同侧时(如图1),求证:AD+BE=DE;
(2)当点D,E分别在AB的异侧(如图2,图3时),线段AD,DE之间又有怎样的关系,请直接写出结论.
2018-2019学年黑龙江省鸡西市密山实验中学八年级(上)期中数学试卷(五四学制)
参考答案与试题解析
一、填空题(每小题3分,共30分)
1.(3分)若点P在线段AB的垂直平分线上,PA=5,则PB= 5 .
【分析】根据线段垂直平分线上的点到线段两端点的距离相等可得PB=PA.
【解答】解:∵点P在线段AB的垂直平分线上,
∴PB=PA=5.
故答案为:5.
2.(3分)若分式有意义,则x的取值范围为 x≠1 .
【分析】分式有意义,分母不等于零.
【解答】解:依题意得 x﹣1≠0,即x≠7时有意义.
故答案是:x≠6.
3.(3分)已知点A(x,﹣4)与点B(3,y)关于x轴对称 7 .
【分析】根据关于x轴对称点的坐标特点:横坐标不变,纵坐标互为相反数可得x、y的值,进而可得x+y的值.
【解答】解:∵点A(x,﹣4)与点B(3,
∴x=4,y=4,
∴x+y=7,
故答案为:3.
4.(3分)如图,在△ABC中,DE是AC的垂直平分线,△ABD的周长为13cm,则△ABC的周长是 19 cm.
【分析】由已知条件,利用线段的垂直平分线的性质,得到AD=CD,AC=2AE,结合周长,进行线段的等量代换可得答案.
【解答】解:∵DE是AC的垂直平分线,
∴AD=CD,AC=2AE=6cm,
又∵△ABD的周长=AB+BD+AD=13cm,
∴AB+BD+CD=13cm,
即AB+BC=13cm,
∴△ABC的周长=AB+BC+AC=13+5=19cm.
故答案为19.
5.(3分)如图,在Rt△ABC中,∠C=90°,BD是∠ABC的平分线,若BD=10 5 .
【分析】求出∠ABC,求出∠DBC,根据含30度角的直角三角形性质求出DC=BD,代入求出即可.
【解答】解:∵∠C=90°,∠A=30°,
∴∠ABC=180°﹣30°﹣90°=60°,
∵BD是∠ABC的平分线,
∴∠DBC=∠ABC=30°,
∵∠C=90°,
∴CD=BD=,
故答案为:5.
6.(3分)如图,在△ABC中,AB=AC,若∠A=40°,则∠ABD= 30° .
【分析】根据等腰三角形两底角相等求出∠ABC=∠C,再求出∠CBD,然后根据∠ABD=∠ABC﹣∠CBD代入数据计算即可得解.
【解答】解:∵AB=AC,∠A=40°,
∴∠ABC=∠C=(180°﹣40°)=70°,
∵BD=BC,
∴∠CBD=180°﹣70°×4=40°,
∴∠ABD=∠ABC﹣∠CBD
=70°﹣40°
=30°.
故答案为:30°.
7.(3分)当a ≠ 时,(a﹣)0=1.
【分析】直接利用零指数幂的性质分析得出答案.
【解答】解:当a≠时,(a﹣)0=6.
故答案为:≠.
8.(3分)若5x﹣3y﹣2=0,则105x÷103y= 100 .
【分析】根据同底数幂的除法法则,可将所求代数式化为:105x﹣3y,而5x﹣3y的值可由已知的方程求出,然后代数求值即可.
【解答】解:∵5x﹣3y﹣4=0,
∴5x﹣2y=2,
∴105x÷107y=105x﹣3y=107=100.
9.(3分)在平面直角坐标系中,已知A坐标(﹣2,2),在y轴上确定一点P,则符合条件的点P共有 4 个.
【分析】分类讨论:①以OP为底时;②以AP为底时;③以AO为底边时.在直角坐标系中利用辅助线即可得到点P的位置.
【解答】解:因为△AOP为等腰三角形,所以可分成三类讨论:
①AO=AP(有一个),
此时只要以A为圆心AO长为半径画圆,可知圆与y轴交于O点和另一个点;
②AO=OP(有两个),
此时只要以O为圆心AO长为半径画圆,可知圆与y轴交于两个点;
③AP=OP(一个),
作AO的中垂线,与y轴有一个交点.
综上所述,共有4个.
故答案为:4.
10.(3分)观察下列图形它们是按一定规律排列的,依照此规律,第20个图形共有 60 个★.
【分析】排列组成的图形都是三角形.第一个图形中有1×3=3个★,
第二个图形中有2×3=6个★,
第三个图形中有3×3=9个★,
…
第20个图形共有20×3=60个★.
【解答】解:根据规律可知
第n个图形有3n个★,
所以第20个图形共有20×3=60个★.
二、选择题(每小题3分,共30分)
11.(3分)下列计算中正确的是( )
A.a2+b3=2a5 B.a4÷a=a4 C.a2 a4=a8 D.(﹣a2)3=﹣a6
【分析】根据合并同类项,可判断A;根据同底数幂的除法,可判断B;根据同底数幂的乘法,可判断C;根据积的乘方,可判断D.
【解答】解:A、不是同类项不能合并;
B、同底数幂的除法底数不变指数相减;
C、同底数幂的乘法底数不变指数相加;
D、积的乘方等于乘方的积;
故选:D.
12.(3分)下面有4个汽车标志图案,其中是轴对称图形的是( )
A.②③④ B.①③④ C.①②④ D.①②③
【分析】利用轴对称图形性质,关于某条直线对称的图形叫轴对称图形得出即可.
【解答】解:只有第4个不是轴对称图形,其它3个都是轴对称图形.
故选:D.
13.(3分)如图,已知△ABC是等边三角形,点O是BC上任意一点,OF分别于两边垂直,等边三角形的高为2( )
A.1 B.3 C.2 D.4
【分析】利用等边三角形的特殊角求出OE与OF的和,可得出其与三角形的高相等,进而可得出结论.
【解答】解:∵△ABC是等边三角形,
∴AB=BC=AC,∠A=∠B=∠C=60°
又∵OE⊥AB,OF⊥AC,
∴OE=OB sin60°=OBOC.
∴OE+OF=(OB+OC)=.
在等边△ABC中,高h=BC.
∴OE+OF=h.
又∵等边三角形的高为2,
∴OE+OF=2,
解法二:三角形ABC的面积等于三角形AOB的面积+三角形AOC的面积,三角形ABC是等边三角形,高OF+高OE等于三角形ABC的高2.
故选:C.
14.(3分)如图,AC=BC=10cm,∠B=15°,则AD的长为( )
A.3cm B.4cm C.5cm D.6cm
【分析】根据等边对等角的性质可得∠B=∠BAC,再根据三角形的一个外角等于与它不相邻的两个内角的和列式求出∠ACD=30°,然后根据直角三角形30°角所对的直角边等于斜边的一半解答即可.
【解答】解:∵AC=BC,
∴∠B=∠BAC=15°,
∴∠ACD=∠B+∠BAC=15°+15°=30°,
∵AD⊥BC,
∴AD=AC=.
故选:C.
15.(3分)若x2+kxy+9y2是一个完全平方式,则k的取值为( )
A.±6 B.6 C.3 D.±81
【分析】根据完全平方式的定义解决此题.
【解答】解:x2+kxy+9y5=x2+kxy+(3y)8.
∵x2+kxy+9y2是一个完全平方式,
∴kxy=±2x 3y=±2xy.
∴k=±6.
故选:A.
16.(3分)已知a2+b2=25,且ab=12,则(a+b)2的值是( )
A.13 B.49 C.37 D.1
【分析】根据完全平方公式解决此题.
【解答】解:∵a2+b2=25,ab=12,
∴(a+b)2=a2+b2+8ab=25+2×12=49.
故选:B.
17.(3分)下列约分正确的是( )
A. B.
C. D.
【分析】根据分式的基本性质作答.
【解答】解:A、,错误;
B、,错误;
C、,正确;
D、,错误.
故选:C.
18.(3分)已知等腰三角形一腰上的高与另一腰的夹角为60°,则这个等腰三角形的顶角是( )
A.30° B.60° C.150° D.30°或150°
【分析】读到此题我们首先想到等腰三角形分为锐角、直角、钝角等腰三角形,当为等腰直角三角形时不可能出现题中所说情况所以舍去不计,我们可以通过画图来讨论剩余两种情况.
【解答】解:①当为锐角三角形时可以画图,
高与左边腰成60°夹角,由三角形内角和为180°可得,
②当为钝角三角形时可画图,
此时垂足落到三角形外面,因为三角形内角和为180°,
由图可以看出等腰三角形的顶角的补角为30°,
∴三角形的顶角为150°,
故选:D.
19.(3分)如(x+m)与(x+3)的乘积中不含x的一次项,则m的值为( )
A.﹣3 B.3 C.0 D.1
【分析】先用多项式乘以多项式的运算法则展开求它们的积,并且把m看作常数合并关于x的同类项,令x的系数为0,得出关于m的方程,求出m的值.
【解答】解:∵(x+m)(x+3)=x2+8x+mx+3m=x2+(8+m)x+3m,
又∵(x+m)与(x+3)的乘积中不含x的一次项,
∴4+m=0,
解得m=﹣3.
故选:A.
20.(3分)如图所示,已知△ABC和△CDE均是等边三角形,点B、C、D在同一条直线上,AD与CE交于点N,AC与BE交于点M,则下列结论:①AD=BE;②AN=BM;④∠BOC=∠DOC,⑤△CMN为等边三角形,则∠BED=100°.其中正确的结论个数为( )
A.3个 B.4个 C.5个 D.6个
【分析】根据等边三角形的性质可得AC=BC,CD=CE,∠ACB=∠DCE,再求出∠ACD=∠BCE,然后利用“边角边”证明△ACD和△BCE全等,根据全等三角形对应边相等可得AD=BE,判断出①正确,全等三角形对应角相等可得∠ADC=∠BEC,∠CAD=∠CBE,再求出∠ACN=∠BCM=60°,然后利用“边角边”证明△ACN和△BCM全等,根据全等三角形对应边相等可得AN=BM,CM=CN,判断出②正确,利用全等三角形的性质得出BE=AD,S△ACD=S△BCE,由角平分线的性质得到∠BOC=∠DOC,判断出④正确;判断出△CMN为等边三角形,判断出⑤正确,根据等边三角形的性质可得∠CMN=60°,得到∠ACB=∠CMN,再根据内错角相等,两直线平行可得MN∥BD,判断出③正确;求出∠ADC,即为∠BEC,再根据∠BED=∠BEC+∠CED计算即可得解,从而判断出⑥正确.
【解答】解:∵△ABC和△CDE均是等边三角形,
∴AC=BC,CD=CE,
∴∠ACB+∠ACE=∠DCE+∠ACE,
即∠ACD=∠BCE,
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS),
∴AD=BE,(故①正确);
∠ADC=∠BEC,∠CAD=∠CBE,
∵∠ACN=180°﹣2×60°=60°,
∴∠ACN=∠BCM=60°,
在△ACN和△BCM中,
,
∴△ACN≌△BCM(ASA),
∴AN=BM,CM=CN,(故②正确);
∵∠ACN=60°,CM=CN,
∴△CMN为等边三角形,(故⑤正确);
∴∠CMN=60°,
∴∠ACB=∠CMN=60°,
∴MN∥BD,(故③正确);
过C作CG⊥BE于G,CH⊥AD于H,
∵△ACD≌△BCE,
∴BE=AD,S△ACD=S△BCE,
∴×BE×CG=,
∴CG=CH,
∵CG⊥BE,CH⊥AD,
∴∠BOC=∠DOC.
故④正确;
∵∠ADE=20°,
∴∠ADC=∠CDE﹣∠ADE=60°﹣20°=40°,
∴∠BEC=40°,
∴∠BED=∠BEC+∠CED=40°+60°=100°,(故⑥正确);
综上所述,结论正确的是①②③④⑤⑥共7个.
故选:D.
三、解答题(共60分)
21.(10分)先化简再求值
(1)x2(x﹣1)﹣x(x2+x﹣1),其中;
(2)(2x+3y)2﹣(2x+y)(2x﹣y)其中.
【分析】(1)先根据单项式乘多项式算乘法,再合并同类项,最后代入求出答案即可;
(2)先根据完全平方公式和平方差公式进行计算,再合并同类项,最后代入求出答案即可.
【解答】解:(1)x2(x﹣1)﹣x(x2+x﹣1)
=x3﹣x4﹣x3﹣x2+x
=﹣8x2+x,
当时,原式=﹣2×()2+=0;
(2)(2x+2y)2﹣(2x+y)(5x﹣y)
=4x2+12xy+3y2﹣4x2+y2
=12xy+10y2,
当时,原式=12×)+10×(﹣)2
=﹣2+8.5
=0.2.
22.(8分)计算
(1)(x﹣2)(x2+4);
(2)(6x4÷8x3)÷(﹣2x2);
(3)(2a﹣3b)(3b+2a);
(4)(2a+b+c)2.
【分析】(1)利用多项式乘多项式法则计算可求解;
(2)利用多项式除以单项式法则计算可求解;
(3)利用多项式乘多项式法则计算可求解;
(4)利用完全平方公式计算,再利用完全平方公式及单项式乘多项式法则计算可求解.
【解答】解:(1)(x﹣2)(x2+7)
=x3+4x﹣7x2﹣8;
(2)(4x4÷8x5)÷(﹣2x2)
=﹣6x2﹣4x;
(3)(8a﹣3b)(3b+8a)
=6ab+4a3﹣9b2﹣3ab
=4a2﹣2b2;
(4)(2a+b+c)5
=(2a+b)2+6(2a+b)c+c2
=6a2+4ab+b7+4ac+2bc+c5.
23.(8分)因式分解
(1)x3﹣9x;
(2)25x2﹣16y2;
(3)(m+n)2﹣4m(m+n)+4m2;
(4)(a﹣b)2+4ab.
【分析】(1)先提公因式,再利用平方差公式即可;
(2)直接利用平方差公式即可;
(3)直接利用完全平方公式即可进行因式分解;
(4)先进行整理,再利用完全平方公式即可.
【解答】解:(1)原式=x(x2﹣9)
=x(x+2)(x﹣3);
(2)原式=(5x+3y)(5x﹣4y);
(3)原式=[(m+n)﹣7m]2
=(n﹣m)2;
(4)原式=a5﹣2ab+b2+5ab
=a2+2ab+b8
=(a+b)2.
24.(4分)已知(x+y)2=25,(x﹣y)2=9,求xy与x2+y2的值.
【分析】利用完全平方公式把已知条件展开,然后相减即可求出xy的值,相加即可求出x2+y2的值.
【解答】解:∵(x+y)2=25,(x﹣y)2=4,
∴x2+2xy+y2=25①,
x2﹣2xy+y3=9②,
①﹣②得,4xy=16,
①+②得,6(x2+y2)=34,解得x6+y2=17.
故答案为:4,17.
25.(6分)如图,在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
(1)求出△ABC的面积;
(2)在图中作出△ABC关于y轴的对称图形△A1B1C1;
(3)写出点A1,B1,C1的坐标.
【分析】(1)利用三角形的面积求法即可得出答案;
(2)首先找出A、B、C三点关于y轴的对称点,再顺次连接即可;
(3)根据坐标系写出各点坐标即可.
【解答】解:(1)如图所示:△ABC的面积:×8×5=7.7;
(2)如图所示:
(3)A1(1,8),B1(1,8),C1(4,3).
26.(6分)如图△ABC是等边三角形,BD是中线,延长BC到E
【分析】根据等边三角形的性质得到∠ABC=∠ACB=60°,∠DBC=30°,再根据角之间的关系求得∠DBC=∠CED,根据等角对等边即可得到DB=DE.
【解答】证明:∵△ABC是等边三角形,BD是中线,
∴∠ABC=∠ACB=60°.
∠DBC=30°(等腰三角形三线合一).
又∵CE=CD,
∴∠CDE=∠CED.
又∵∠BCD=∠CDE+∠CED,
∴∠CDE=∠CED=∠BCD=30°.
∴∠DBC=∠DEC.
∴DB=DE(等角对等边).
27.(8分)如图:在△ABC中,BO平分∠ABC,CO平分∠ACB,且MN∥BC,求证:△AMN的周长等于AB+AC.
【分析】根据角平分线的定义可得∠ABO=∠CBO,根据两直线平行,内错角相等可得∠CBO=∠BOM,从而得到∠ABO=∠BOM,再根据等角对等边可得BM=OM,同理可得CN=ON,然后即可求出△AMN的周长=AB+AC.
【解答】解:∵BO平分∠ABC,
∴∠ABO=∠CBO,
∵MN∥BC,
∴∠CBO=∠BOM,
∴∠ABO=∠BOM,
∴BM=OM,
同理可得CN=ON,
∴△AMN的周长=AM+MO+ON+AN=AM+BM+CN+AN=AB+AC.
28.(10分)已知等腰直角△ABC,直线l经过点C,过点A,垂足分别为D,E.
(1)当点D,E分别在AB的同侧时(如图1),求证:AD+BE=DE;
(2)当点D,E分别在AB的异侧(如图2,图3时),线段AD,DE之间又有怎样的关系,请直接写出结论.
【分析】(1)K型全等模型的基本型,通过在△ACD和△BCE中利用角的互余关系证明等角,从而证明全等;
(2)由(1)的思路可得结论.
【解答】(1)证明:在Rt△ADC中,∠ACD+∠CAD=90°,
在Rt△BEC中,∠ACD+∠BCE=90°,
∴∠CAD=∠BCE,
在△ACD和△CBE中,
,
∴△ACD≌△CBE(AAS),
∴AD=CE,CD=EB,
∵CE+CD=DE,
∴AD+BE=DE.
(2)图2中,BE+DE=AD,
证明:在Rt△ADC中,∠ACD+∠CAD=90°,
∵∠ACB=90°,
∴∠ACD+∠BCE=90°,
∴∠CAD=∠BCE,
在△ACD和△CBE中,
,
∴△ACD≌△CBE(AAS),
∴AD=CE,CD=EB,
∵CD+DE=CE,
∴BE+DE=AD.
图3中,AD+DE=BE,
证明:在Rt△ADC中,∠ACD+∠CAD=90°,
∵∠ACB=90°,
∴∠ACD+∠BCE=90°,
∴∠CAD=∠BCE,
∴∠CAD=∠BCE,
在△ACD和△CBE中,
,
∴△ACD≌△CBE(AAS),
∴AD=CE,CD=EB,
∵CE+DE=CD,
∴AD+DE=BE.
一、填空题(每小题3分,共30分)
1.(3分)若点P在线段AB的垂直平分线上,PA=5,则PB= .
2.(3分)若分式有意义,则x的取值范围为 .
3.(3分)已知点A(x,﹣4)与点B(3,y)关于x轴对称 .
4.(3分)如图,在△ABC中,DE是AC的垂直平分线,△ABD的周长为13cm,则△ABC的周长是 cm.
5.(3分)如图,在Rt△ABC中,∠C=90°,BD是∠ABC的平分线,若BD=10 .
6.(3分)如图,在△ABC中,AB=AC,若∠A=40°,则∠ABD= .
7.(3分)当a 时,(a﹣)0=1.
8.(3分)若5x﹣3y﹣2=0,则105x÷103y= .
9.(3分)在平面直角坐标系中,已知A坐标(﹣2,2),在y轴上确定一点P,则符合条件的点P共有 个.
10.(3分)观察下列图形它们是按一定规律排列的,依照此规律,第20个图形共有 个★.
二、选择题(每小题3分,共30分)
11.(3分)下列计算中正确的是( )
A.a2+b3=2a5 B.a4÷a=a4 C.a2 a4=a8 D.(﹣a2)3=﹣a6
12.(3分)下面有4个汽车标志图案,其中是轴对称图形的是( )
A.②③④ B.①③④ C.①②④ D.①②③
13.(3分)如图,已知△ABC是等边三角形,点O是BC上任意一点,OF分别于两边垂直,等边三角形的高为2( )
A.1 B.3 C.2 D.4
14.(3分)如图,AC=BC=10cm,∠B=15°,则AD的长为( )
A.3cm B.4cm C.5cm D.6cm
15.(3分)若x2+kxy+9y2是一个完全平方式,则k的取值为( )
A.±6 B.6 C.3 D.±81
16.(3分)已知a2+b2=25,且ab=12,则(a+b)2的值是( )
A.13 B.49 C.37 D.1
17.(3分)下列约分正确的是( )
A. B.
C. D.
18.(3分)已知等腰三角形一腰上的高与另一腰的夹角为60°,则这个等腰三角形的顶角是( )
A.30° B.60° C.150° D.30°或150°
19.(3分)如(x+m)与(x+3)的乘积中不含x的一次项,则m的值为( )
A.﹣3 B.3 C.0 D.1
20.(3分)如图所示,已知△ABC和△CDE均是等边三角形,点B、C、D在同一条直线上,AD与CE交于点N,AC与BE交于点M,则下列结论:①AD=BE;②AN=BM;④∠BOC=∠DOC,⑤△CMN为等边三角形,则∠BED=100°.其中正确的结论个数为( )
A.3个 B.4个 C.5个 D.6个
三、解答题(共60分)
21.(10分)先化简再求值
(1)x2(x﹣1)﹣x(x2+x﹣1),其中;
(2)(2x+3y)2﹣(2x+y)(2x﹣y)其中.
22.(8分)计算
(1)(x﹣2)(x2+4);
(2)(6x4÷8x3)÷(﹣2x2);
(3)(2a﹣3b)(3b+2a);
(4)(2a+b+c)2.
23.(8分)因式分解
(1)x3﹣9x;
(2)25x2﹣16y2;
(3)(m+n)2﹣4m(m+n)+4m2;
(4)(a﹣b)2+4ab.
24.(4分)已知(x+y)2=25,(x﹣y)2=9,求xy与x2+y2的值.
25.(6分)如图,在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
(1)求出△ABC的面积;
(2)在图中作出△ABC关于y轴的对称图形△A1B1C1;
(3)写出点A1,B1,C1的坐标.
26.(6分)如图△ABC是等边三角形,BD是中线,延长BC到E
27.(8分)如图:在△ABC中,BO平分∠ABC,CO平分∠ACB,且MN∥BC,求证:△AMN的周长等于AB+AC.
28.(10分)已知等腰直角△ABC,直线l经过点C,过点A,垂足分别为D,E.
(1)当点D,E分别在AB的同侧时(如图1),求证:AD+BE=DE;
(2)当点D,E分别在AB的异侧(如图2,图3时),线段AD,DE之间又有怎样的关系,请直接写出结论.
2018-2019学年黑龙江省鸡西市密山实验中学八年级(上)期中数学试卷(五四学制)
参考答案与试题解析
一、填空题(每小题3分,共30分)
1.(3分)若点P在线段AB的垂直平分线上,PA=5,则PB= 5 .
【分析】根据线段垂直平分线上的点到线段两端点的距离相等可得PB=PA.
【解答】解:∵点P在线段AB的垂直平分线上,
∴PB=PA=5.
故答案为:5.
2.(3分)若分式有意义,则x的取值范围为 x≠1 .
【分析】分式有意义,分母不等于零.
【解答】解:依题意得 x﹣1≠0,即x≠7时有意义.
故答案是:x≠6.
3.(3分)已知点A(x,﹣4)与点B(3,y)关于x轴对称 7 .
【分析】根据关于x轴对称点的坐标特点:横坐标不变,纵坐标互为相反数可得x、y的值,进而可得x+y的值.
【解答】解:∵点A(x,﹣4)与点B(3,
∴x=4,y=4,
∴x+y=7,
故答案为:3.
4.(3分)如图,在△ABC中,DE是AC的垂直平分线,△ABD的周长为13cm,则△ABC的周长是 19 cm.
【分析】由已知条件,利用线段的垂直平分线的性质,得到AD=CD,AC=2AE,结合周长,进行线段的等量代换可得答案.
【解答】解:∵DE是AC的垂直平分线,
∴AD=CD,AC=2AE=6cm,
又∵△ABD的周长=AB+BD+AD=13cm,
∴AB+BD+CD=13cm,
即AB+BC=13cm,
∴△ABC的周长=AB+BC+AC=13+5=19cm.
故答案为19.
5.(3分)如图,在Rt△ABC中,∠C=90°,BD是∠ABC的平分线,若BD=10 5 .
【分析】求出∠ABC,求出∠DBC,根据含30度角的直角三角形性质求出DC=BD,代入求出即可.
【解答】解:∵∠C=90°,∠A=30°,
∴∠ABC=180°﹣30°﹣90°=60°,
∵BD是∠ABC的平分线,
∴∠DBC=∠ABC=30°,
∵∠C=90°,
∴CD=BD=,
故答案为:5.
6.(3分)如图,在△ABC中,AB=AC,若∠A=40°,则∠ABD= 30° .
【分析】根据等腰三角形两底角相等求出∠ABC=∠C,再求出∠CBD,然后根据∠ABD=∠ABC﹣∠CBD代入数据计算即可得解.
【解答】解:∵AB=AC,∠A=40°,
∴∠ABC=∠C=(180°﹣40°)=70°,
∵BD=BC,
∴∠CBD=180°﹣70°×4=40°,
∴∠ABD=∠ABC﹣∠CBD
=70°﹣40°
=30°.
故答案为:30°.
7.(3分)当a ≠ 时,(a﹣)0=1.
【分析】直接利用零指数幂的性质分析得出答案.
【解答】解:当a≠时,(a﹣)0=6.
故答案为:≠.
8.(3分)若5x﹣3y﹣2=0,则105x÷103y= 100 .
【分析】根据同底数幂的除法法则,可将所求代数式化为:105x﹣3y,而5x﹣3y的值可由已知的方程求出,然后代数求值即可.
【解答】解:∵5x﹣3y﹣4=0,
∴5x﹣2y=2,
∴105x÷107y=105x﹣3y=107=100.
9.(3分)在平面直角坐标系中,已知A坐标(﹣2,2),在y轴上确定一点P,则符合条件的点P共有 4 个.
【分析】分类讨论:①以OP为底时;②以AP为底时;③以AO为底边时.在直角坐标系中利用辅助线即可得到点P的位置.
【解答】解:因为△AOP为等腰三角形,所以可分成三类讨论:
①AO=AP(有一个),
此时只要以A为圆心AO长为半径画圆,可知圆与y轴交于O点和另一个点;
②AO=OP(有两个),
此时只要以O为圆心AO长为半径画圆,可知圆与y轴交于两个点;
③AP=OP(一个),
作AO的中垂线,与y轴有一个交点.
综上所述,共有4个.
故答案为:4.
10.(3分)观察下列图形它们是按一定规律排列的,依照此规律,第20个图形共有 60 个★.
【分析】排列组成的图形都是三角形.第一个图形中有1×3=3个★,
第二个图形中有2×3=6个★,
第三个图形中有3×3=9个★,
…
第20个图形共有20×3=60个★.
【解答】解:根据规律可知
第n个图形有3n个★,
所以第20个图形共有20×3=60个★.
二、选择题(每小题3分,共30分)
11.(3分)下列计算中正确的是( )
A.a2+b3=2a5 B.a4÷a=a4 C.a2 a4=a8 D.(﹣a2)3=﹣a6
【分析】根据合并同类项,可判断A;根据同底数幂的除法,可判断B;根据同底数幂的乘法,可判断C;根据积的乘方,可判断D.
【解答】解:A、不是同类项不能合并;
B、同底数幂的除法底数不变指数相减;
C、同底数幂的乘法底数不变指数相加;
D、积的乘方等于乘方的积;
故选:D.
12.(3分)下面有4个汽车标志图案,其中是轴对称图形的是( )
A.②③④ B.①③④ C.①②④ D.①②③
【分析】利用轴对称图形性质,关于某条直线对称的图形叫轴对称图形得出即可.
【解答】解:只有第4个不是轴对称图形,其它3个都是轴对称图形.
故选:D.
13.(3分)如图,已知△ABC是等边三角形,点O是BC上任意一点,OF分别于两边垂直,等边三角形的高为2( )
A.1 B.3 C.2 D.4
【分析】利用等边三角形的特殊角求出OE与OF的和,可得出其与三角形的高相等,进而可得出结论.
【解答】解:∵△ABC是等边三角形,
∴AB=BC=AC,∠A=∠B=∠C=60°
又∵OE⊥AB,OF⊥AC,
∴OE=OB sin60°=OBOC.
∴OE+OF=(OB+OC)=.
在等边△ABC中,高h=BC.
∴OE+OF=h.
又∵等边三角形的高为2,
∴OE+OF=2,
解法二:三角形ABC的面积等于三角形AOB的面积+三角形AOC的面积,三角形ABC是等边三角形,高OF+高OE等于三角形ABC的高2.
故选:C.
14.(3分)如图,AC=BC=10cm,∠B=15°,则AD的长为( )
A.3cm B.4cm C.5cm D.6cm
【分析】根据等边对等角的性质可得∠B=∠BAC,再根据三角形的一个外角等于与它不相邻的两个内角的和列式求出∠ACD=30°,然后根据直角三角形30°角所对的直角边等于斜边的一半解答即可.
【解答】解:∵AC=BC,
∴∠B=∠BAC=15°,
∴∠ACD=∠B+∠BAC=15°+15°=30°,
∵AD⊥BC,
∴AD=AC=.
故选:C.
15.(3分)若x2+kxy+9y2是一个完全平方式,则k的取值为( )
A.±6 B.6 C.3 D.±81
【分析】根据完全平方式的定义解决此题.
【解答】解:x2+kxy+9y5=x2+kxy+(3y)8.
∵x2+kxy+9y2是一个完全平方式,
∴kxy=±2x 3y=±2xy.
∴k=±6.
故选:A.
16.(3分)已知a2+b2=25,且ab=12,则(a+b)2的值是( )
A.13 B.49 C.37 D.1
【分析】根据完全平方公式解决此题.
【解答】解:∵a2+b2=25,ab=12,
∴(a+b)2=a2+b2+8ab=25+2×12=49.
故选:B.
17.(3分)下列约分正确的是( )
A. B.
C. D.
【分析】根据分式的基本性质作答.
【解答】解:A、,错误;
B、,错误;
C、,正确;
D、,错误.
故选:C.
18.(3分)已知等腰三角形一腰上的高与另一腰的夹角为60°,则这个等腰三角形的顶角是( )
A.30° B.60° C.150° D.30°或150°
【分析】读到此题我们首先想到等腰三角形分为锐角、直角、钝角等腰三角形,当为等腰直角三角形时不可能出现题中所说情况所以舍去不计,我们可以通过画图来讨论剩余两种情况.
【解答】解:①当为锐角三角形时可以画图,
高与左边腰成60°夹角,由三角形内角和为180°可得,
②当为钝角三角形时可画图,
此时垂足落到三角形外面,因为三角形内角和为180°,
由图可以看出等腰三角形的顶角的补角为30°,
∴三角形的顶角为150°,
故选:D.
19.(3分)如(x+m)与(x+3)的乘积中不含x的一次项,则m的值为( )
A.﹣3 B.3 C.0 D.1
【分析】先用多项式乘以多项式的运算法则展开求它们的积,并且把m看作常数合并关于x的同类项,令x的系数为0,得出关于m的方程,求出m的值.
【解答】解:∵(x+m)(x+3)=x2+8x+mx+3m=x2+(8+m)x+3m,
又∵(x+m)与(x+3)的乘积中不含x的一次项,
∴4+m=0,
解得m=﹣3.
故选:A.
20.(3分)如图所示,已知△ABC和△CDE均是等边三角形,点B、C、D在同一条直线上,AD与CE交于点N,AC与BE交于点M,则下列结论:①AD=BE;②AN=BM;④∠BOC=∠DOC,⑤△CMN为等边三角形,则∠BED=100°.其中正确的结论个数为( )
A.3个 B.4个 C.5个 D.6个
【分析】根据等边三角形的性质可得AC=BC,CD=CE,∠ACB=∠DCE,再求出∠ACD=∠BCE,然后利用“边角边”证明△ACD和△BCE全等,根据全等三角形对应边相等可得AD=BE,判断出①正确,全等三角形对应角相等可得∠ADC=∠BEC,∠CAD=∠CBE,再求出∠ACN=∠BCM=60°,然后利用“边角边”证明△ACN和△BCM全等,根据全等三角形对应边相等可得AN=BM,CM=CN,判断出②正确,利用全等三角形的性质得出BE=AD,S△ACD=S△BCE,由角平分线的性质得到∠BOC=∠DOC,判断出④正确;判断出△CMN为等边三角形,判断出⑤正确,根据等边三角形的性质可得∠CMN=60°,得到∠ACB=∠CMN,再根据内错角相等,两直线平行可得MN∥BD,判断出③正确;求出∠ADC,即为∠BEC,再根据∠BED=∠BEC+∠CED计算即可得解,从而判断出⑥正确.
【解答】解:∵△ABC和△CDE均是等边三角形,
∴AC=BC,CD=CE,
∴∠ACB+∠ACE=∠DCE+∠ACE,
即∠ACD=∠BCE,
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS),
∴AD=BE,(故①正确);
∠ADC=∠BEC,∠CAD=∠CBE,
∵∠ACN=180°﹣2×60°=60°,
∴∠ACN=∠BCM=60°,
在△ACN和△BCM中,
,
∴△ACN≌△BCM(ASA),
∴AN=BM,CM=CN,(故②正确);
∵∠ACN=60°,CM=CN,
∴△CMN为等边三角形,(故⑤正确);
∴∠CMN=60°,
∴∠ACB=∠CMN=60°,
∴MN∥BD,(故③正确);
过C作CG⊥BE于G,CH⊥AD于H,
∵△ACD≌△BCE,
∴BE=AD,S△ACD=S△BCE,
∴×BE×CG=,
∴CG=CH,
∵CG⊥BE,CH⊥AD,
∴∠BOC=∠DOC.
故④正确;
∵∠ADE=20°,
∴∠ADC=∠CDE﹣∠ADE=60°﹣20°=40°,
∴∠BEC=40°,
∴∠BED=∠BEC+∠CED=40°+60°=100°,(故⑥正确);
综上所述,结论正确的是①②③④⑤⑥共7个.
故选:D.
三、解答题(共60分)
21.(10分)先化简再求值
(1)x2(x﹣1)﹣x(x2+x﹣1),其中;
(2)(2x+3y)2﹣(2x+y)(2x﹣y)其中.
【分析】(1)先根据单项式乘多项式算乘法,再合并同类项,最后代入求出答案即可;
(2)先根据完全平方公式和平方差公式进行计算,再合并同类项,最后代入求出答案即可.
【解答】解:(1)x2(x﹣1)﹣x(x2+x﹣1)
=x3﹣x4﹣x3﹣x2+x
=﹣8x2+x,
当时,原式=﹣2×()2+=0;
(2)(2x+2y)2﹣(2x+y)(5x﹣y)
=4x2+12xy+3y2﹣4x2+y2
=12xy+10y2,
当时,原式=12×)+10×(﹣)2
=﹣2+8.5
=0.2.
22.(8分)计算
(1)(x﹣2)(x2+4);
(2)(6x4÷8x3)÷(﹣2x2);
(3)(2a﹣3b)(3b+2a);
(4)(2a+b+c)2.
【分析】(1)利用多项式乘多项式法则计算可求解;
(2)利用多项式除以单项式法则计算可求解;
(3)利用多项式乘多项式法则计算可求解;
(4)利用完全平方公式计算,再利用完全平方公式及单项式乘多项式法则计算可求解.
【解答】解:(1)(x﹣2)(x2+7)
=x3+4x﹣7x2﹣8;
(2)(4x4÷8x5)÷(﹣2x2)
=﹣6x2﹣4x;
(3)(8a﹣3b)(3b+8a)
=6ab+4a3﹣9b2﹣3ab
=4a2﹣2b2;
(4)(2a+b+c)5
=(2a+b)2+6(2a+b)c+c2
=6a2+4ab+b7+4ac+2bc+c5.
23.(8分)因式分解
(1)x3﹣9x;
(2)25x2﹣16y2;
(3)(m+n)2﹣4m(m+n)+4m2;
(4)(a﹣b)2+4ab.
【分析】(1)先提公因式,再利用平方差公式即可;
(2)直接利用平方差公式即可;
(3)直接利用完全平方公式即可进行因式分解;
(4)先进行整理,再利用完全平方公式即可.
【解答】解:(1)原式=x(x2﹣9)
=x(x+2)(x﹣3);
(2)原式=(5x+3y)(5x﹣4y);
(3)原式=[(m+n)﹣7m]2
=(n﹣m)2;
(4)原式=a5﹣2ab+b2+5ab
=a2+2ab+b8
=(a+b)2.
24.(4分)已知(x+y)2=25,(x﹣y)2=9,求xy与x2+y2的值.
【分析】利用完全平方公式把已知条件展开,然后相减即可求出xy的值,相加即可求出x2+y2的值.
【解答】解:∵(x+y)2=25,(x﹣y)2=4,
∴x2+2xy+y2=25①,
x2﹣2xy+y3=9②,
①﹣②得,4xy=16,
①+②得,6(x2+y2)=34,解得x6+y2=17.
故答案为:4,17.
25.(6分)如图,在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
(1)求出△ABC的面积;
(2)在图中作出△ABC关于y轴的对称图形△A1B1C1;
(3)写出点A1,B1,C1的坐标.
【分析】(1)利用三角形的面积求法即可得出答案;
(2)首先找出A、B、C三点关于y轴的对称点,再顺次连接即可;
(3)根据坐标系写出各点坐标即可.
【解答】解:(1)如图所示:△ABC的面积:×8×5=7.7;
(2)如图所示:
(3)A1(1,8),B1(1,8),C1(4,3).
26.(6分)如图△ABC是等边三角形,BD是中线,延长BC到E
【分析】根据等边三角形的性质得到∠ABC=∠ACB=60°,∠DBC=30°,再根据角之间的关系求得∠DBC=∠CED,根据等角对等边即可得到DB=DE.
【解答】证明:∵△ABC是等边三角形,BD是中线,
∴∠ABC=∠ACB=60°.
∠DBC=30°(等腰三角形三线合一).
又∵CE=CD,
∴∠CDE=∠CED.
又∵∠BCD=∠CDE+∠CED,
∴∠CDE=∠CED=∠BCD=30°.
∴∠DBC=∠DEC.
∴DB=DE(等角对等边).
27.(8分)如图:在△ABC中,BO平分∠ABC,CO平分∠ACB,且MN∥BC,求证:△AMN的周长等于AB+AC.
【分析】根据角平分线的定义可得∠ABO=∠CBO,根据两直线平行,内错角相等可得∠CBO=∠BOM,从而得到∠ABO=∠BOM,再根据等角对等边可得BM=OM,同理可得CN=ON,然后即可求出△AMN的周长=AB+AC.
【解答】解:∵BO平分∠ABC,
∴∠ABO=∠CBO,
∵MN∥BC,
∴∠CBO=∠BOM,
∴∠ABO=∠BOM,
∴BM=OM,
同理可得CN=ON,
∴△AMN的周长=AM+MO+ON+AN=AM+BM+CN+AN=AB+AC.
28.(10分)已知等腰直角△ABC,直线l经过点C,过点A,垂足分别为D,E.
(1)当点D,E分别在AB的同侧时(如图1),求证:AD+BE=DE;
(2)当点D,E分别在AB的异侧(如图2,图3时),线段AD,DE之间又有怎样的关系,请直接写出结论.
【分析】(1)K型全等模型的基本型,通过在△ACD和△BCE中利用角的互余关系证明等角,从而证明全等;
(2)由(1)的思路可得结论.
【解答】(1)证明:在Rt△ADC中,∠ACD+∠CAD=90°,
在Rt△BEC中,∠ACD+∠BCE=90°,
∴∠CAD=∠BCE,
在△ACD和△CBE中,
,
∴△ACD≌△CBE(AAS),
∴AD=CE,CD=EB,
∵CE+CD=DE,
∴AD+BE=DE.
(2)图2中,BE+DE=AD,
证明:在Rt△ADC中,∠ACD+∠CAD=90°,
∵∠ACB=90°,
∴∠ACD+∠BCE=90°,
∴∠CAD=∠BCE,
在△ACD和△CBE中,
,
∴△ACD≌△CBE(AAS),
∴AD=CE,CD=EB,
∵CD+DE=CE,
∴BE+DE=AD.
图3中,AD+DE=BE,
证明:在Rt△ADC中,∠ACD+∠CAD=90°,
∵∠ACB=90°,
∴∠ACD+∠BCE=90°,
∴∠CAD=∠BCE,
∴∠CAD=∠BCE,
在△ACD和△CBE中,
,
∴△ACD≌△CBE(AAS),
∴AD=CE,CD=EB,
∵CE+DE=CD,
∴AD+DE=BE.
同课章节目录
