人教版2021-2022学年八年级上册数学 13.1.2线段的垂直平分线的性质课件(共17张PPT)
文档属性
| 名称 | 人教版2021-2022学年八年级上册数学 13.1.2线段的垂直平分线的性质课件(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-01 15:28:38 | ||
图片预览




文档简介
(共17张PPT)
THE HEADLINE
01
线段的垂直平分线的性质
THE HEADLINE
01
PART
问题:
已知线段AB,除线段AB的中点C外,线段的对称轴上是否还存在其他的点到点A和点B的距离相等呢?
找一找,有多少个?
你发现了什么?
结论1
线段垂直平分线上的点
与这条线段两个端点的距离相等
01
直尺测量
圆规测距
对折重合 ……
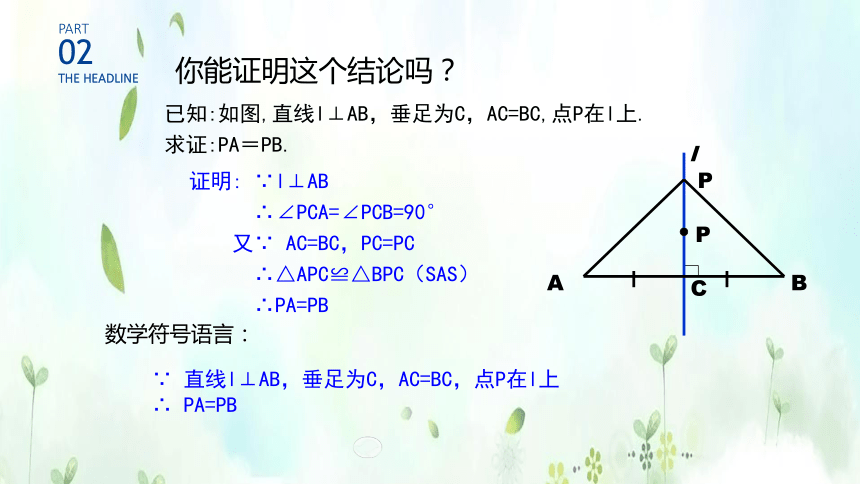
你能证明这个结论吗?
已知:如图,直线l⊥AB,垂足为C,AC=BC,点P在l上.
求证:PA=PB.
证明: ∵l⊥AB
∴∠PCA=∠PCB=90°
又∵ AC=BC,PC=PC
∴△APC≌△BPC(SAS)
∴PA=PB
A
C
B
P
l
∵ 直线l⊥AB,垂足为C,AC=BC,点P在l上
∴ PA=PB
数学符号语言:
THE HEADLINE
02
PART
P
问题
1.将结论中的两端点变为线段上的任意两点,结论还成立吗?
02
2.直线l为线段AB的垂直平分线,点P不在l上,PA还等于PB吗?
03
THE HEADLINE
03
PART
结论2
与线段两个端点的距离相等的点在这条线段的垂直平分线上
THE HEADLINE
04
PART
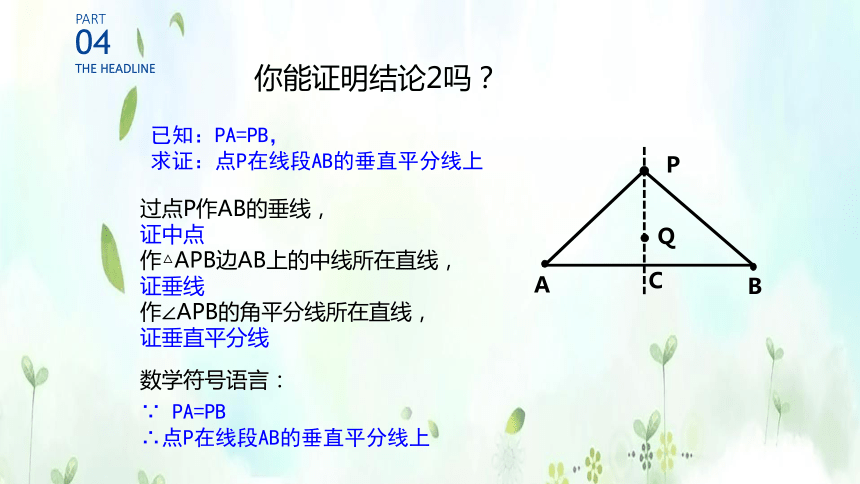
已知:PA=PB,
求证:点P在线段AB的垂直平分线上
P
A
B
过点P作AB的垂线,
证中点
作△APB边AB上的中线所在直线,
证垂线
作∠APB的角平分线所在直线,
证垂直平分线
C
你能证明结论2吗?
Q
∵ PA=PB
∴点P在线段AB的垂直平分线上
数学符号语言:
结论2:
A
C
B
P
l
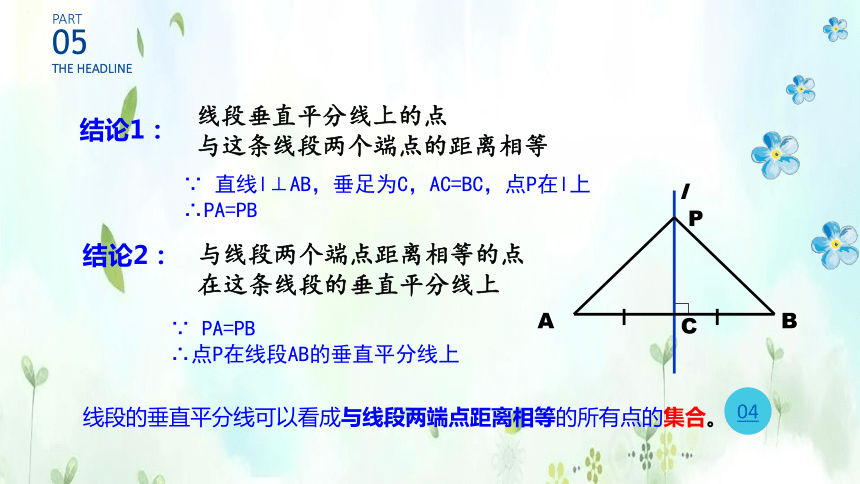
与线段两个端点距离相等的点
在这条线段的垂直平分线上
线段的垂直平分线可以看成与线段两端点距离相等的所有点的集合。
结论1:
线段垂直平分线上的点
与这条线段两个端点的距离相等
∵ 直线l⊥AB,垂足为C,AC=BC,点P在l上
∴PA=PB
∵ PA=PB
∴点P在线段AB的垂直平分线上
THE HEADLINE
05
PART
04
尺规作图:已知线段AB
求作:作出线段AB的垂直平分线。
THE HEADLINE
06
PART
尺规作图:经过已知直线外一点作这条直线的垂线:
已知:直线AB和直线AB外一点C
求作:AB的垂线,使它经过点C.
作法:
(1)任意取一点K,使点K和点C在AB的两旁.
(2)以点C为圆心,CK长为半径作弧,交AB于点D和E.
(3)分别以点D和点E为圆心,大于1/2DE的长为半径作弧,两弧相交于点F.
(4)作直线CF.
直线CF就是所求作的垂线.
C
K
A
B
D
E
F
THE HEADLINE
07
PART
本节课你学到了哪些知识?
掌握了哪些方法?
THE HEADLINE
08
PART
1:如图,在△ABC中,AB的垂直平分线交BC边于点E.
(1)若BE=3cm,则AE= cm。
(2)若BC=6cm,△AEC的周长9cm,则AC= cm。
THE HEADLINE
09
PART
3
3
2.如图,已知,PA=PB,MA=MB,
求证:AN=BN
证明:
∵PA=PB
∴点P在AB的垂直平分线上
∵MA=MB
∴点M在AB的垂直平分线上
∴直线PM是线段AB的垂直平分线
∴AN=BN
THE HEADLINE
10
PART
(1)本节课学习了哪些内容?
(2)线段垂直平分线的性质和判定是如何得到的?
两者之间有什么关系?
(3)如何判断一条直线是否是线段的垂直平分线?
小结
1.如图所示,AC=AD,BC=BD,则下列说法正确的
是( )
A.AB垂直平分CD;
B .CD垂直平分AB ;
C.AB与CD互相垂直平分;
D.CD平分∠ ACB .
A
B
C
D
练习
2.在锐角三角形ABC内一点P,,满足PA=PB=PC,
则点P是△ABC ( )
A.三条角平分线的交点
B.三条中线的交点
C.三条高的交点
D.三边垂直平分线的交点
Summer a lot of things began to trivial for example, I hide in behind the morning in a hurry to eat text, breathed life back to the story, then through these years of ladder to update a day in and day out of
康托尔,德国数学家,集合论的创始人
在数学的领域中,提出问题的艺术比解答问题的艺术更为重要。
Thank You
Add Your Text Here
THE HEADLINE
01
线段的垂直平分线的性质
THE HEADLINE
01
PART
问题:
已知线段AB,除线段AB的中点C外,线段的对称轴上是否还存在其他的点到点A和点B的距离相等呢?
找一找,有多少个?
你发现了什么?
结论1
线段垂直平分线上的点
与这条线段两个端点的距离相等
01
直尺测量
圆规测距
对折重合 ……
你能证明这个结论吗?
已知:如图,直线l⊥AB,垂足为C,AC=BC,点P在l上.
求证:PA=PB.
证明: ∵l⊥AB
∴∠PCA=∠PCB=90°
又∵ AC=BC,PC=PC
∴△APC≌△BPC(SAS)
∴PA=PB
A
C
B
P
l
∵ 直线l⊥AB,垂足为C,AC=BC,点P在l上
∴ PA=PB
数学符号语言:
THE HEADLINE
02
PART
P
问题
1.将结论中的两端点变为线段上的任意两点,结论还成立吗?
02
2.直线l为线段AB的垂直平分线,点P不在l上,PA还等于PB吗?
03
THE HEADLINE
03
PART
结论2
与线段两个端点的距离相等的点在这条线段的垂直平分线上
THE HEADLINE
04
PART
已知:PA=PB,
求证:点P在线段AB的垂直平分线上
P
A
B
过点P作AB的垂线,
证中点
作△APB边AB上的中线所在直线,
证垂线
作∠APB的角平分线所在直线,
证垂直平分线
C
你能证明结论2吗?
Q
∵ PA=PB
∴点P在线段AB的垂直平分线上
数学符号语言:
结论2:
A
C
B
P
l
与线段两个端点距离相等的点
在这条线段的垂直平分线上
线段的垂直平分线可以看成与线段两端点距离相等的所有点的集合。
结论1:
线段垂直平分线上的点
与这条线段两个端点的距离相等
∵ 直线l⊥AB,垂足为C,AC=BC,点P在l上
∴PA=PB
∵ PA=PB
∴点P在线段AB的垂直平分线上
THE HEADLINE
05
PART
04
尺规作图:已知线段AB
求作:作出线段AB的垂直平分线。
THE HEADLINE
06
PART
尺规作图:经过已知直线外一点作这条直线的垂线:
已知:直线AB和直线AB外一点C
求作:AB的垂线,使它经过点C.
作法:
(1)任意取一点K,使点K和点C在AB的两旁.
(2)以点C为圆心,CK长为半径作弧,交AB于点D和E.
(3)分别以点D和点E为圆心,大于1/2DE的长为半径作弧,两弧相交于点F.
(4)作直线CF.
直线CF就是所求作的垂线.
C
K
A
B
D
E
F
THE HEADLINE
07
PART
本节课你学到了哪些知识?
掌握了哪些方法?
THE HEADLINE
08
PART
1:如图,在△ABC中,AB的垂直平分线交BC边于点E.
(1)若BE=3cm,则AE= cm。
(2)若BC=6cm,△AEC的周长9cm,则AC= cm。
THE HEADLINE
09
PART
3
3
2.如图,已知,PA=PB,MA=MB,
求证:AN=BN
证明:
∵PA=PB
∴点P在AB的垂直平分线上
∵MA=MB
∴点M在AB的垂直平分线上
∴直线PM是线段AB的垂直平分线
∴AN=BN
THE HEADLINE
10
PART
(1)本节课学习了哪些内容?
(2)线段垂直平分线的性质和判定是如何得到的?
两者之间有什么关系?
(3)如何判断一条直线是否是线段的垂直平分线?
小结
1.如图所示,AC=AD,BC=BD,则下列说法正确的
是( )
A.AB垂直平分CD;
B .CD垂直平分AB ;
C.AB与CD互相垂直平分;
D.CD平分∠ ACB .
A
B
C
D
练习
2.在锐角三角形ABC内一点P,,满足PA=PB=PC,
则点P是△ABC ( )
A.三条角平分线的交点
B.三条中线的交点
C.三条高的交点
D.三边垂直平分线的交点
Summer a lot of things began to trivial for example, I hide in behind the morning in a hurry to eat text, breathed life back to the story, then through these years of ladder to update a day in and day out of
康托尔,德国数学家,集合论的创始人
在数学的领域中,提出问题的艺术比解答问题的艺术更为重要。
Thank You
Add Your Text Here
