人教版2021-2022学年八年级上册数学14.2.1平方差公式 课件(共21张PPT)
文档属性
| 名称 | 人教版2021-2022学年八年级上册数学14.2.1平方差公式 课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 258.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-01 00:00:00 | ||
图片预览







文档简介
(共21张PPT)
平方差公式
人教版八年级数学上册
第十四章《整式的乘法与因式分解》第二节《乘法公式》第一课时
探究:
计算下列多项式的积:
(1) (x+1)(x-1) =
(2) (1+2x)(1-2x) =
(3) (3m+n)(3m-n) =
9m2 - n2
X2-1
1- 4x2
=x2 - 12
=12- (2x)2
=(3m)2 - n2
猜想:
两个数的和与这两个数的差的积,
等于这两个数的平方差。
怎样验证?
a2-b2
(a+b)(a-b) =
用字母a、b表示为:
验证(代数方法):
(a+b)(a-b) = a2-b2
左边 =(a+b)(a-b)
= a2-ab+ab-b2
-ab
+ab
= a2-b2
a2
b2
左边=右边
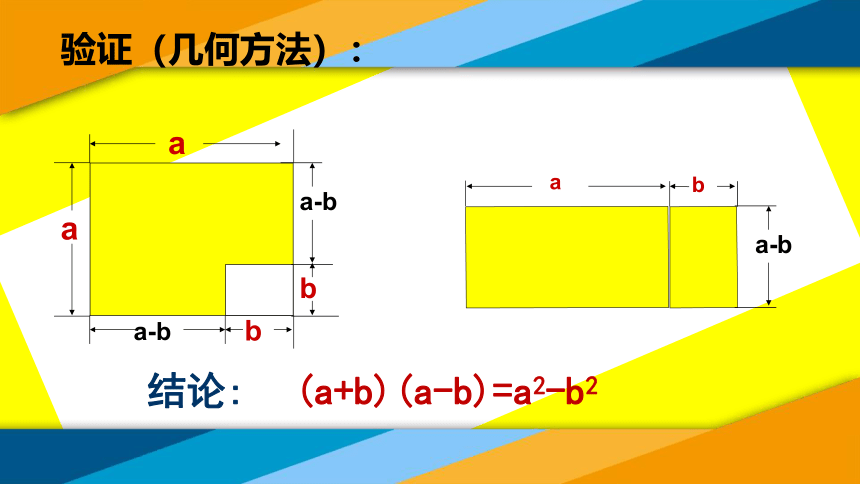
验证(几何方法):
b
b
a
a
a-b
a-b
a
b
a-b
(a+b)(a-b)=a2-b2
结论:
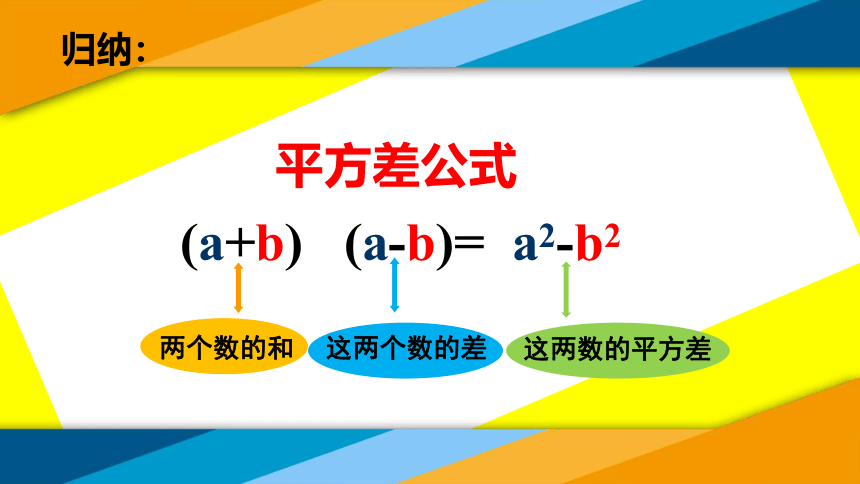
归纳:
(a+b) (a-b)= a2-b2
两个数的和
这两个数的差
这两数的平方差
平方差公式
归纳:
(a+b)(a-b)=a2-b2
特征:
相同项
平方差公式
归纳:
特征:
符号相反的项
(a+b)(a-b)=a2-b2
平方差公式
归纳:
(a+b)(a-b)=a2-b2
(相同项)2-(符号相反项)2
平方差公式
找一找、填一填
a
b
a2-b2
1
x
12-x2
-3
a
(-3)2-a2
a
1
a2-12
0.3x
1
( 0.3x)2-12
(a-b)(a+b)
(1+a)(-1+a)
(0.3x-1)(1+0.3x)
(-3+a)(-3-a)
(1+x)(1-x)
运用:
友情提示:
公式中的a、b可以是数字,可以是单个的字母,还可以是整式。
运用:
(1) (a+2b)( a 2b);
(2) (a 2b)(2b a) ;
(3) (2a+b)(b+2a);
(4) (a 3b)(a+3b) ;
(5) ( 2x+3y)(3y 2x).
(不能)
(不存在相同的项)
(不能)
(不能)
(能)
(a2 9b2)=
a2 + 9b2 ;
(不能)
判断下列式子能否用平方差公式计算:
平方差公式
(不存在符号相反的项)
(不存在符号相反的项)
(不存在相同的项)
注意:两个乘式中完全相同的项是a,只有符号相反的项的绝对值是b。
例1:
运用平方差公式计算:
⑴ (3x+2)(3x-2) ;
(3) ( - x2 )(-x2- ).
(4) 102 ×98
(2)
运用:
运用:
运用平方差公式计算:
1、(m+n)(-n+m) =
2、(-x-y) (x-y) =
3、(2a+b)(2a-b) =
4、(x2+y2)(x2-y2)=
5、 51 × 49 =
m2-n2
位置变化
y2-x2
符号变化
4a2-b2
系数变化
x4-y4
指数变化
2499
无中生有
运用:
计算:
1、(3x+4)(3x-4)–(2x+3)(3x-2);
2、3×5×17
例2:
运用:
灵活运用平方差公式计算
3、 (x+y)(x-y)(x2+y2)
4、 20202-2019×2021
2、 (y+2)(y-2)-(y-1)(y+5)
1、 99×101×10001
拓展:
下列各式计算中能用平方差公式吗?
①(m+n+1)(m+n-1)
②(-m+n+1)(m+n-1)
③(-m+n+1)(m-n-1)
平方差公式
拓展:
灵活运用平方差公式计算
(m+n+1)(m+n-1)=63,求m+n的值
平方差公式
1. 试用语言表述平方差公式 (a+b)(a b)=a2 b2。
两数和与这两数差的积,等于它们的平方差。
2.应用平方差公式 时要注意一些什么?
紧扣公式的特征,找出与公式对应的“a”和“b”,然后运用公式进行计算
小结:
平方差公式
作业:
平方差公式
课本P 156 T 1
同步练习册P98
谢谢您的指导!
平方差公式
人教版八年级数学上册
第十四章《整式的乘法与因式分解》第二节《乘法公式》第一课时
探究:
计算下列多项式的积:
(1) (x+1)(x-1) =
(2) (1+2x)(1-2x) =
(3) (3m+n)(3m-n) =
9m2 - n2
X2-1
1- 4x2
=x2 - 12
=12- (2x)2
=(3m)2 - n2
猜想:
两个数的和与这两个数的差的积,
等于这两个数的平方差。
怎样验证?
a2-b2
(a+b)(a-b) =
用字母a、b表示为:
验证(代数方法):
(a+b)(a-b) = a2-b2
左边 =(a+b)(a-b)
= a2-ab+ab-b2
-ab
+ab
= a2-b2
a2
b2
左边=右边
验证(几何方法):
b
b
a
a
a-b
a-b
a
b
a-b
(a+b)(a-b)=a2-b2
结论:
归纳:
(a+b) (a-b)= a2-b2
两个数的和
这两个数的差
这两数的平方差
平方差公式
归纳:
(a+b)(a-b)=a2-b2
特征:
相同项
平方差公式
归纳:
特征:
符号相反的项
(a+b)(a-b)=a2-b2
平方差公式
归纳:
(a+b)(a-b)=a2-b2
(相同项)2-(符号相反项)2
平方差公式
找一找、填一填
a
b
a2-b2
1
x
12-x2
-3
a
(-3)2-a2
a
1
a2-12
0.3x
1
( 0.3x)2-12
(a-b)(a+b)
(1+a)(-1+a)
(0.3x-1)(1+0.3x)
(-3+a)(-3-a)
(1+x)(1-x)
运用:
友情提示:
公式中的a、b可以是数字,可以是单个的字母,还可以是整式。
运用:
(1) (a+2b)( a 2b);
(2) (a 2b)(2b a) ;
(3) (2a+b)(b+2a);
(4) (a 3b)(a+3b) ;
(5) ( 2x+3y)(3y 2x).
(不能)
(不存在相同的项)
(不能)
(不能)
(能)
(a2 9b2)=
a2 + 9b2 ;
(不能)
判断下列式子能否用平方差公式计算:
平方差公式
(不存在符号相反的项)
(不存在符号相反的项)
(不存在相同的项)
注意:两个乘式中完全相同的项是a,只有符号相反的项的绝对值是b。
例1:
运用平方差公式计算:
⑴ (3x+2)(3x-2) ;
(3) ( - x2 )(-x2- ).
(4) 102 ×98
(2)
运用:
运用:
运用平方差公式计算:
1、(m+n)(-n+m) =
2、(-x-y) (x-y) =
3、(2a+b)(2a-b) =
4、(x2+y2)(x2-y2)=
5、 51 × 49 =
m2-n2
位置变化
y2-x2
符号变化
4a2-b2
系数变化
x4-y4
指数变化
2499
无中生有
运用:
计算:
1、(3x+4)(3x-4)–(2x+3)(3x-2);
2、3×5×17
例2:
运用:
灵活运用平方差公式计算
3、 (x+y)(x-y)(x2+y2)
4、 20202-2019×2021
2、 (y+2)(y-2)-(y-1)(y+5)
1、 99×101×10001
拓展:
下列各式计算中能用平方差公式吗?
①(m+n+1)(m+n-1)
②(-m+n+1)(m+n-1)
③(-m+n+1)(m-n-1)
平方差公式
拓展:
灵活运用平方差公式计算
(m+n+1)(m+n-1)=63,求m+n的值
平方差公式
1. 试用语言表述平方差公式 (a+b)(a b)=a2 b2。
两数和与这两数差的积,等于它们的平方差。
2.应用平方差公式 时要注意一些什么?
紧扣公式的特征,找出与公式对应的“a”和“b”,然后运用公式进行计算
小结:
平方差公式
作业:
平方差公式
课本P 156 T 1
同步练习册P98
谢谢您的指导!
