北师大版七年级数学上册 2.9 有理数的乘方课件(共22张PPT)
文档属性
| 名称 | 北师大版七年级数学上册 2.9 有理数的乘方课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 962.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-01 15:56:43 | ||
图片预览








文档简介
(共22张PPT)
第二章 有理数及其运算
有理数的乘方
学习目标:
1、在现实背景中,理解有理数乘方的意义。
2、能进行有理数的乘方运算。
3、通过实例感受当底数大于1时,乘方运算的结果增长的很快。
复习提问:
1、有理数乘法法则
2、有理数除法法则
口算:
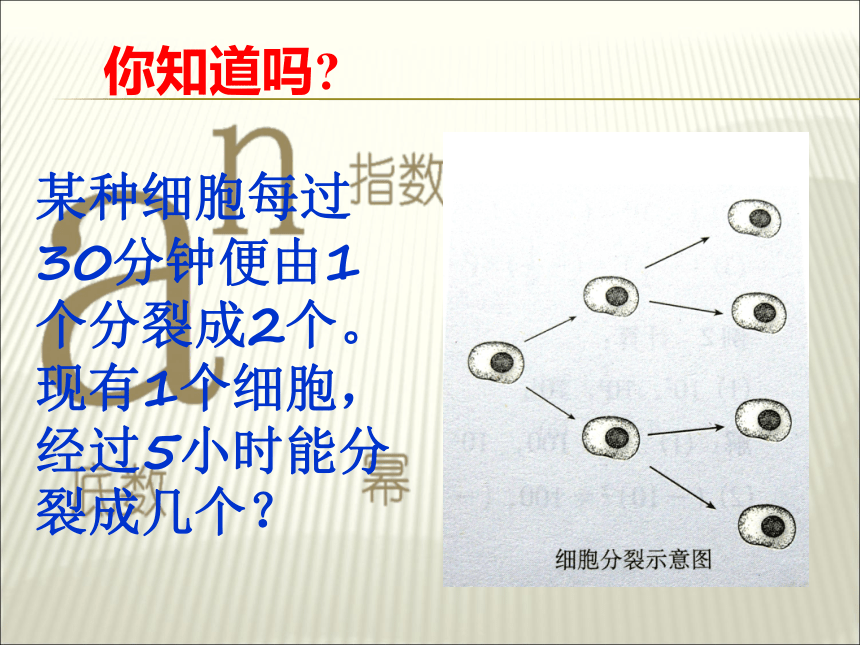
你知道吗
某种细胞每过30分钟便由1个分裂成2个。现有1个细胞,经过5小时能分裂成几个?
第1次分裂成2个,
第2次分裂成2×2个,
第3次分裂成2×2×2个,
………
5小时要分裂十次,所以
第10次分裂成2×2×2………×2×2(10个2)个.
2×2×2………×2×2(共10个2)
有简单的表示方法吗
学习目标:
1、在现实背景中,理解有理数乘方的意义。
2、能进行有理数的乘方运算。
3、通过实例感受当底数大于1时,乘方运算的结果增长得很快。
自学指导:看书第83~84页完成下列各题
1、什么是有理数的乘方?
2、什么是幂?什么是底数?什么是指数?
3、计算例1,例2。
4、观察例2的结果,你能发现什么规律?
a
n
底数
指数
运算的结果叫做幂
2
读做a 的n次方
或a的n次幂。
填空:
(1)(-2)10的底数是___,指数是 ____,读作_________
(2)(-3) 12表示______个_______相乘,读作_________,
(3)( ) 8的指数是________,底数______ 读作_______,
(4)3.6 5 的指数是_________,底数是________,读作_______,
(5)x m 表示____个_____相乘,指数是______,底数是_______,读作_________.
熟悉乘方
例1:计算
例题讲解
解:
计算
① (-3)3;② (-1.5)2; ③( )2
练一练!
例2:计算
(1)10 ,10 ,10 ;
(2)(-10) ,(-10) ,(-10)
2 3 4
2 3 4
例题讲解
例2:计算
猜一猜:你发现了什么规律
4
规律1:10的几次幂就在1后面加几个0。
规律2:底数为负数时,指数为偶数幂的符号为正,指数为奇数时幂的符号为负。
有理数乘方运算的符号法则 :
正数的任何次方都是正数,
负数的偶数次的幂是正数,
负数的奇数次的幂是负数.
0的任何次幂等于多少?
1的任何次幂等于多少?
想一想:
联系拓广:
设n为正整数,计算:
本节课同学们学到了哪些知识?
8
小结
教科书习题 2.13,
知识技能1、2、
作业:
1米长的小棒,第1次截去一半,第2次截去剩下的一半,如此截下去,第7次后剩下的小棒有多长?
问题解决:
你见过拉面师傅拉面条吗?拉面师傅先用一根很粗的面条,把两头捏起来拉长,然后再把两头捏起来拉长,不断这样,就将一根面条拉成许多根细面条了,如果要拉出1000多根细面条,拉面师傅要拉多少次?
思考题:
第二章 有理数及其运算
有理数的乘方
学习目标:
1、在现实背景中,理解有理数乘方的意义。
2、能进行有理数的乘方运算。
3、通过实例感受当底数大于1时,乘方运算的结果增长的很快。
复习提问:
1、有理数乘法法则
2、有理数除法法则
口算:
你知道吗
某种细胞每过30分钟便由1个分裂成2个。现有1个细胞,经过5小时能分裂成几个?
第1次分裂成2个,
第2次分裂成2×2个,
第3次分裂成2×2×2个,
………
5小时要分裂十次,所以
第10次分裂成2×2×2………×2×2(10个2)个.
2×2×2………×2×2(共10个2)
有简单的表示方法吗
学习目标:
1、在现实背景中,理解有理数乘方的意义。
2、能进行有理数的乘方运算。
3、通过实例感受当底数大于1时,乘方运算的结果增长得很快。
自学指导:看书第83~84页完成下列各题
1、什么是有理数的乘方?
2、什么是幂?什么是底数?什么是指数?
3、计算例1,例2。
4、观察例2的结果,你能发现什么规律?
a
n
底数
指数
运算的结果叫做幂
2
读做a 的n次方
或a的n次幂。
填空:
(1)(-2)10的底数是___,指数是 ____,读作_________
(2)(-3) 12表示______个_______相乘,读作_________,
(3)( ) 8的指数是________,底数______ 读作_______,
(4)3.6 5 的指数是_________,底数是________,读作_______,
(5)x m 表示____个_____相乘,指数是______,底数是_______,读作_________.
熟悉乘方
例1:计算
例题讲解
解:
计算
① (-3)3;② (-1.5)2; ③( )2
练一练!
例2:计算
(1)10 ,10 ,10 ;
(2)(-10) ,(-10) ,(-10)
2 3 4
2 3 4
例题讲解
例2:计算
猜一猜:你发现了什么规律
4
规律1:10的几次幂就在1后面加几个0。
规律2:底数为负数时,指数为偶数幂的符号为正,指数为奇数时幂的符号为负。
有理数乘方运算的符号法则 :
正数的任何次方都是正数,
负数的偶数次的幂是正数,
负数的奇数次的幂是负数.
0的任何次幂等于多少?
1的任何次幂等于多少?
想一想:
联系拓广:
设n为正整数,计算:
本节课同学们学到了哪些知识?
8
小结
教科书习题 2.13,
知识技能1、2、
作业:
1米长的小棒,第1次截去一半,第2次截去剩下的一半,如此截下去,第7次后剩下的小棒有多长?
问题解决:
你见过拉面师傅拉面条吗?拉面师傅先用一根很粗的面条,把两头捏起来拉长,然后再把两头捏起来拉长,不断这样,就将一根面条拉成许多根细面条了,如果要拉出1000多根细面条,拉面师傅要拉多少次?
思考题:
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
